Оценка погрешностей измерений при проведении школьного физического эксперимента

Обновлено: 02.07.2024

Цель работы: получение и закрепление навыков обработки результатов прямых, косвенных и совместных измерений.

Основные теоретические сведения

Прямые измерения

Одной из важнейших задач физического эксперимента являются измерения величин. Процесс измерения состоит в том, что измеряемую величину сравнивают с другой величиной, принятой за эталон. Измерения, в процессе которых искомая величина определяется с помощью специально предназначенного для этого прибора, называются прямыми. Они никогда не бывают абсолютно точными. Всегда возникает разброс результатов измерений, что требует оценки погрешности (ошибки)- обязательного элемента любого эксперимента. Род и причины погрешностей разнообразны и необходимы многочисленные эксперименты, чтобы их систематизировать.

систематические погрешности- это погрешности, являющиеся следствием неправильной калибровки (сбитый ноль прибора, тепловое расширение линейки.), ошибочности метода измерений и т.п. При наличии такого типа погрешностей измеренное значение отклоняется от истинного значения в одну и ту же сторону и на одну и туже величину. Повторными измерениями эти ошибки не уменьшаются, однако их можно оценить методом сравнения результатов измерений заданной величины каким-либо прибором с измерениями, полученными исправным прибором (с большей степенью точности).
случайные погрешности вносятся изменчивыми условиями эксперимента, несовершенством органов чувств и трудно учитываемыми условиями эксперимента, ограниченной точностью и т.п. Случайные ошибки уменьшаются с ростом числа измерений пропорционально , (где - число измерений в одинаковых условиях) и подчиняются законам теории вероятности и математической статистики. Чаще всего случайные погрешности проявляются в виде разброса (рассеяния) показаний прибора. В результате этого разброса измеряемая величина случайным образом отклоняется от истинного значения в произвольную сторону на произвольную величину.
промахи- погрешности, чаще всего возникающие вследствие невнимательности человека или недостаточной его квалификации и опыта. Их можно наблюдать, например, при неправильном отсчете измеряемого значения (неправильное определение цены деления прибора). Кроме того, к грубым погрешностям могут привести внезапные сильные внешние влияния на измерительное устройство, повреждения или помехи, которые нельзя считать субъективными.
приборные погрешности- этот тип погрешностей обусловлен тем, что практически любое измерительное устройство обладает ограниченной степенью точности, т.е. ,например, измерительной линейкой с ценой деления 1см нельзя измерить длину стола с точностью до одного миллиметра. Практически для большинства измерительных устройств (за исключением электроизмерительных приборов) в качестве приборной погрешности принимается половина его цены деления.
погрешности округления - связаны с тем, что в расчетах приходится те или иные величины округлять до определенного десятичного разряда.

Далее введем понятие дисперсии выборки, являющейся мерой отклонений измеренных значений от их среднего значения . Дисперсию выборки находят из следующего соотношения

Величина, которая является мерой отклонения среднего значения выборки от истинного значения измеряемой величины, называется дисперсией среднего значения. Дисперсия среднего значения обозначается и вычисляется по формуле:

Величина , равная называется среднеквадратичным отклонением среднего значения от истинного значения . Очевидно, что среднее значение и дисперсия зависят как от измеренных значений , так и от объема выборки . Причем, при увеличении до бесконечности среднее значение и дисперсия выборки стремятся, соответственно, к среднему значению и дисперсии генеральной совокупности. Дисперсию генеральной совокупности обычно обозначают .

Результаты измерений величины являются случайными числами, поскольку при измерениях присутствуют случайные погрешности измерений. Наиболее часто вероятность получения результата измерений описывается распределением Гаусса. Плотностью распределения величины называется функция , такая, что вероятность получить измеряемую величину в интервале от до равна ,

Н
а рис 0.1 представлен график функции . Важнейшим свойством ее является то, что вероятность получения результата однократного измерения равна площади под кривой в пределах до . Например, в пределах от до вероятность равна 0.683, в пределах от до она равна 0.954 и в пределах , до она будет 0.997 . Следовательно, из 1000 измерений 683 наиболее вероятно попадут в интервал , 954 -в интервал , а 997 соответственно в интервал .

Рисунок 0.1. График функции распределения Гаусса.

Целью физического эксперимента при проведении прямых измерений является определение интервала, в котором находится истинное значение величины (доверительного интервала). Чтобы записать данный интервал по результатам измерений, в которых присутствуют только случайные погрешности, предварительно введем параметр, определяемый по формуле

где - истинное значение измеряемой величины.

Из данного соотношения видно, что параметр также является величиной случайной, поскольку находится из случайных величин и . Следовательно, для всевозможных значений параметра также существует своя функция распределения. Впервые данная зависимость была найдена Стьюдентом и получила название функции распределения Стьюдента, а параметр называется параметром Стьюдента. Аналитическое выражения функции распределения параметра Стьюдента имеет следующий вид:

, где гамма функция.

График функции распределения параметра Стьюдента представлен на рисунке 0.2. Зная данное распределение и используя следующее равенство можно вычислить вероятность того, что параметр не превосходит значения .

Р
исунок 0.2. График функции распределения параметра Стьюдента.

Обычно на практике поступают по иному. Зная количество измерений , и задавая вероятность , находят величину параметра . Значения данного параметра приведены в табл. 0.1. Данные таблицы 0.1 на практике используют следующим образом. Зная объем выборки и задавая значение вероятности , с помощью табл. 0.1 находят параметр , где -число степеней свободы ( ). После чего из соотношения (0.5) легко получить искомый интервал

при , равном заданному значению, и соответствующем .

Данная запись означает то, что истинное значение величины с вероятностью , попадает в указанный интервал. В том случае, если при проведении прямых измерений присутствуют кроме случайных погрешностей и другие виды погрешностей необходимо также учитывать их влияние на искажения полученных результатов. В этом случае дисперсию прямых измерений находят по формуле:

где - дисперсия измерений от случайных погрешностей, - дисперсия измерений от приборных погрешностей и т.д. Следует заметить, что из полученных прямых измерений оценить систематическую погрешность не представляется возможным.

Шкала – это показывающая часть измерительного прибора, состоящая из упорядоченного ряда отметок со связанной с ними нумерацией. Шкала может располагаться по окружности, дуге или прямой линии.

Примеры шкал различных приборов:

Манометр – прибор для измерения давления, круговая шкала

Вольтметр – прибор для измерения напряжения, дуговая шкала

Индикатор громкости звука, линейная шкала

п.2. Цена деления

Цена деления измерительного прибора равна числу единиц измеряемой величины между двумя ближайшими делениями шкалы. Как правило, цена деления указана на маркировке прибора.

Алгоритм определения цены деления
Шаг 1. Найти два ближайшие пронумерованные крупные деления шкалы. Пусть первое значение равно a, второе равно b, b > a.
Шаг 2. Посчитать количество мелких делений шкалы между ними. Пусть это количество равно n.
Шаг 3. Разделить разницу значений крупных делений шкалы на количество отрезков, которые образуются мелкими делениями: $$ \triangle=\frac $$ Найденное значение $\triangle$ и есть цена деления данного прибора.

Пример определения цены деления:

п.3. Виды измерений

Прямое измерение

Физическую величину измеряют с помощью прибора

Измерение длины бруска линейкой

Косвенное измерение

Физическую величину рассчитывают по формуле, куда подставляют значения величин, полученных с помощью прямых измерений

Определение площади столешницы при измеренной длине и ширине

п.4. Погрешность измерений, абсолютная и относительная погрешность

Инструментальная погрешность

Определяется погрешностью инструментов и приборов, используемых для измерений (принципом действия, точностью шкалы и т.п.)

Погрешность метода

Определяется несовершенством методов и допущениями в методике.

Погрешность теории (модели)

Определяется теоретическими упрощениями, степенью соответствия теоретической модели и реальности.

Погрешность оператора

Определяется субъективным фактором, ошибками экспериментатора.

Инструментальная погрешность измерений принимается равной половине цены деления прибора: $$ d=\frac $$

Если величина $a_0$ - это истинное значение, а $\triangle a$ - погрешность измерения, результат измерений физической величины записывают в виде $a=a_0\pm\triangle a$.

Абсолютная погрешность измерения – это модуль разности между измеренным и истинным значением измеряемой величины: $$ \triangle a=|a-a_0| $$

Отношение абсолютной погрешности измерения к истинному значению, выраженное в процентах, называют относительной погрешностью измерения: $$ \delta=\frac\cdot 100\text $$

Относительная погрешность является мерой точности измерения : чем меньше относительная погрешность, тем измерение точнее. По абсолютной погрешности о точности измерения судить нельзя.
На практике абсолютную и относительную погрешности округляют до двух значащих цифр с избытком , т.е. всегда в сторону увеличения.

Значащие цифры – это все верные цифры числа, кроме нулей слева. Результаты измерений записывают только значащими цифрами.

Примеры значащих цифр:
0,403 – три значащих цифры, величина определена с точностью до тысячных.
40,3 – три значащих цифры, величина определена с точностью до десятых.
40,300 – пять значащих цифр, величина определена с точностью до тысячных.

В простейших измерениях инструментальная погрешность прибора является основной.
В таких случаях физическую величину измеряют один раз, полученное значение берут в качестве истинного, а абсолютную погрешность считают равной инструментальной погрешности прибора.
Примеры измерений с абсолютной погрешностью равной инструментальной:

определение длины с помощью линейки или мерной ленты;
определение объема с помощью мензурки.

Пример получения результатов прямых измерений с помощью линейки:

Измерим длину бруска линейкой, у которой пронумерованы сантиметры и есть только одно деление между пронумерованными делениями.
Цена деления такой линейки: \begin \triangle=\frac= \frac>=0,5\ \text \end Инструментальная погрешность: \begin d=\frac=\frac=0,25\ \text \end Истинное значение: $L_0=4\ \text$
Результат измерений: $$ L=L_0\pm d=(4,00\pm 0,25)\ \text $$ Относительная погрешность: $$ \delta=\frac\cdot 100\text=6,25\text\approx 6,3\text $$

Теперь возьмем линейку с n=9 мелкими делениями между пронумерованными делениями.
Цена деления такой линейки: \begin \triangle=\frac= \frac>=0,1\ \text \end Инструментальная погрешность: \begin d=\frac=\frac=0,05\ \text \end Истинное значение: $L_0=4,15\ \text$
Результат измерений: $$ L=L_0\pm d=(4,15\pm 0,05)\ \text $$ Относительная погрешность: $$ \delta=\frac\cdot 100\text\approx 1,2\text $$

Второе измерение точнее, т.к. его относительная погрешность меньше.

п.5. Абсолютная погрешность серии измерений

Измерение длины с помощью линейки (или объема с помощью мензурки) являются теми редкими случаями, когда для определения истинного значения достаточно одного измерения, а абсолютная погрешность сразу берется равной инструментальной погрешности, т.е. половине цены деления линейки (или мензурки).

Гораздо чаще погрешность метода или погрешность оператора оказываются заметно больше инструментальной погрешности. В таких случаях значение измеренной физической величины каждый раз немного меняется, и для оценки истинного значения и абсолютной погрешности нужна серия измерений и вычисление средних значений.

Алгоритм определения истинного значения и абсолютной погрешности в серии измерений
Шаг 1. Проводим серию из $N$ измерений, в каждом из которых получаем значение величины $x_1,x_2,…,x_N$
Шаг 2. Истинное значение величины принимаем равным среднему арифметическому всех измерений: $$ x_0=x_=\frac $$ Шаг 3. Находим абсолютные отклонения от истинного значения для каждого измерения: $$ \triangle_1=|x_0-x_1|,\ \ \triangle_2=|x_0-x_2|,\ \ . \ \ \triangle_N=|x_0-x_N| $$ Шаг 4. Находим среднее арифметическое всех абсолютных отклонений: $$ \triangle_=\frac $$ Шаг 5. Сравниваем полученную величину $\triangle_$ c инструментальной погрешностью прибора d (половина цены деления). Большую из этих двух величин принимаем за абсолютную погрешность: $$ \triangle x=max\left\<\triangle_; d\right\> $$ Шаг 6. Записываем результат серии измерений: $x=x_0\pm\triangle x$.

Пример расчета истинного значения и погрешности для серии прямых измерений:
Пусть при измерении массы шарика с помощью рычажных весов мы получили в трех опытах следующие значения: 99,8 г; 101,2 г; 100,3 г.
Инструментальная погрешность весов d = 0,05 г.
Найдем истинное значение массы и абсолютную погрешность.

Составим расчетную таблицу:

Сначала находим среднее значение всех измерений: \begin m_0=\frac=\frac\approx 100,4\ \text \end Это среднее значение принимаем за истинное значение массы.
Затем считаем абсолютное отклонение каждого опыта как модуль разности $m_0$ и измерения. \begin \triangle_1=|100,4-99,8|=0,6\\ \triangle_2=|100,4-101,2|=0,8\\ \triangle_3=|100,4-100,3|=0,1 \end Находим среднее абсолютное отклонение: \begin \triangle_=\frac=\frac=0,5\ \text \end Мы видим, что полученное значение $\triangle_$ больше инструментальной погрешности d.
Поэтому абсолютная погрешность измерения массы: \begin \triangle m=max\left\<\triangle_; d\right\>=max\left\\ \text \end Записываем результат: \begin m=m_0\pm\triangle m\\ m=(100,4\pm 0,5)\ \text \end Относительная погрешность (с двумя значащими цифрами): \begin \delta_m=\frac\cdot 100\text\approx 0,050\text \end

п.6. Представление результатов эксперимента

Результат измерения представляется в виде $$ a=a_0\pm\triangle a $$ где $a_0$ – истинное значение, $\triangle a$ – абсолютная погрешность измерения.

Как найти результат прямого измерения, мы рассмотрели выше.
Результат косвенного измерения зависит от действий, которые производятся при подстановке в формулу величин, полученных с помощью прямых измерений.

абсолютная погрешность их суммы равна сумме абсолютных погрешностей

абсолютная погрешность их разности также равна сумме абсолютных погрешностей

относительная погрешность их произведения равна сумме относительных погрешностей

относительная погрешность их частного также равна сумме относительных погрешностей

относительная погрешность квадрата $a^2$ равна удвоенной относительной погрешности

относительная погрешность куба $a^3$ равна утроенной относительной погрешности

относительная погрешность произвольной натуральной степени $a^n$ равна

Вывод этих формул достаточно сложен, но если интересно, его можно найти в Главе 7 справочника по алгебре для 8 класса.

п.7. Задачи

Задача 1. Определите цену деления и объем налитой жидкости для каждой из мензурок. В каком случае измерение наиболее точно; наименее точно?

Составим таблицу для расчета цены деления:

№ мензурки	a, мл	b, мл	n	$\triangle=\frac$, мл
1	20	40	4	$\frac=4$
2	100	200	4	$\frac=20$
3	15	30	4	$\frac=3$
4	200	400	4	$\frac=40$

Инструментальная точность мензурки равна половине цены деления.
Принимаем инструментальную точность за абсолютную погрешность и измеренное значение объема за истинное.
Составим таблицу для расчета относительной погрешности (оставляем две значащих цифры и округляем с избытком):

№ мензурки	Объем $V_0$, мл	Абсолютная погрешность $\triangle V=\frac$, мл	Относительная погрешность $\delta_V=\frac\cdot 100\text$
1	68	2	3,0%
2	280	10	3,6%
3	27	1,5	5,6%
4	480	20	4,2%

Наиболее точное измерение в 1-й мензурке, наименее точное – в 3-й мензурке.

Ответ:
Цена деления 4; 20; 3; 40 мл
Объем 68; 280; 27; 480 мл
Самое точное – 1-я мензурка; самое неточное – 3-я мензурка

Задача 2. В двух научных работах указаны два значения измерений одной и той же величины: $$ x_1=(4,0\pm 0,1)\ \text,\ \ x_2=(4,0\pm 0,03)\ \text $$ Какое из этих измерений точней и почему?

Мерой точности является относительная погрешность измерений. Получаем: \begin \delta_1=\frac\cdot 100\text=2,5\text\\ \delta_2=\frac\cdot 100\text=0,75\text \end Относительная погрешность второго измерения меньше. Значит, второе измерение точней.
Ответ: $\delta_2\lt \delta_1$, второе измерение точней.

Задача 3. Две машины движутся навстречу друг другу со скоростями 54 км/ч и 72 км/ч.
Цена деления спидометра первой машины 10 км/ч, второй машины – 1 км/ч.
Найдите скорость их сближения, абсолютную и относительную погрешность этой величины.

Задача 4. Измеренная длина столешницы равна 90,2 см, ширина 60,1 см. Измерения проводились с помощью линейки с ценой деления 0,1 см. Найдите площадь столешницы, абсолютную и относительную погрешность этой величины.

Инструментальная погрешность линейки $d=\frac=0,05\ \text$
Результаты прямых измерений длины и ширины: $$ a=(90,20\pm 0,05)\ \text,\ \ b=(60,10\pm 0,05)\ \text $$ Относительные погрешности (не забываем про правила округления): \begin \delta_1=\frac\cdot 100\text\approx 0,0554\text\approx \uparrow 0,056\text\\ \delta_2=\frac\cdot 100\text\approx 0,0832\text\approx \uparrow 0,084\text \end Площадь столешницы: $$ S=ab,\ \ S=90,2\cdot 60,1 = 5421,01\ \text^2 $$ Для произведения относительная погрешность равна сумме относительных погрешностей слагаемых: $$ \delta_S=\delta_a+\delta_b=0,056\text+0,084\text=0,140\text=0,14\text $$ Абсолютная погрешность: \begin \triangle S=S\cdot \delta_S=5421,01\cdot 0,0014=7,59\approx 7,6\ \text^2\\ S=(5421,0\pm 7,6)\ \text^2 \end Ответ: $S=(5421,0\pm 7,6)\ \text^2,\ \ \delta_S\approx 0,14\text$

Физика – это наука о природе. Она изучает простейшие и наиболее общие закономерности явлений природы, свойства и строение материи и закономерности ее движения. В основе своей физика – наука экспериментальная: все ее законы и теории исходят и опираются на экспериментальные данные, полученные в результате измерений.

Вопросами измерений занимается метрология: наука об измерениях, методах, средствах обеспечения их единства и способах достижения требуемой точности. Постулаты метрологии:

- У объекта исследования существует определенная характеризующая объект измеряемая величина и ее истинное значение .

- Истинное значение в момент измерения постоянно.

- Существует несоответствие измеряемой величины ее истинному значению.

Истинное значение в экспериментальных измерениях найти невозможно, т.к. любое измерение сопровождается появлением погрешности и, следовательно, имеет некоторую неопределенность. Но по результатам измерений можно оценить с определенной вероятностью.

Если проведены раз измерения некоторой физической величины , в которых получены значения , то в первом приближении истинное значение измеряемой величины можно определить как среднее значение:

где - результат - го измерения.

Среднее значение можно рассматривать как наиболее вероятное значение измеряемой величины. При среднее значение . Отклонение измеряемой величины от истинного значения называют погрешностью измерения:

Однако понятно, что число измерений всегда ограничено. Поэтому истинное значение измеряемой величины оценивают рассчитывая так называемый доверительный интервал , в который с заданной вероятностью входит .

Классификация погрешностей измерений

По характеру проявления

Случайная погрешность - составляющая погрешности результата измерения, которая изменяется случайным образом (по знаку и значению) при повторных измерениях, проводимых с одинаковой тщательностью, одной и той же физической величины.

Причины, приводящие к появлению случайных погрешностей, разнообразны. Они могут иметь как объективный, не зависящий от экспериментатора, характер (изменение температура в процессе измерений, изменение напряжение в электрической цепи, несовершенство методики измерения, конструктивные особенности экспериментальной установки и т.д.), так и субъективный (неопытность экспериментатора, его реакция на наблюдаемое, внимание, психологический настрой и др.). Случайные погрешности имеют неизвестные экспериментатору значения и отличаются в отдельных измерениях; их значения неодинаковы даже для измерений, сделанных в совершенно одинаковых условиях.

При многократных измерениях обычно случайные погрешности одинаковой величины и разные по знаку встречаются с вероятностью, подчиняются нормальному распределению. Поэтому говорят, что измеряемая величина распределена с плотностью вероятности подчиняющейся нормальному закону распределения. Функция плотности вероятности для нормального распределения имеет вид:

где - среднее значение измеряемой величины,

- среднеквадратическое отклонение измеряемой величины.

Графическое изображение нормальной функции плотности вероятности приведено на рисунке 1.

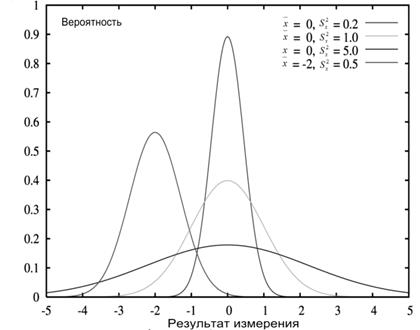
Промах или грубая погрешность – погрешность, возникшая вследствие недосмотра экспериментатора или неисправности измеряющей аппаратуры. Грубые погрешности должны быть исключены из дальнейшей обработки; для этого существует несколько известных критериев и способов [1].

1.2 По форме представления (расчета)

Абсолютная погрешность

Абсолютная погрешность – погрешность измерения, выраженная в единицах измеряемой величины (отклонение измеренного значения от истинного). Она определяется формулой (2), из которой следует, что может иметь как положительные, так и отрицательные значения.

При ограниченном числе измерений (реальная практика измерений), когда , для оценки абсолютной погрешности используется выражение:

В практике расчета погрешностей эксперимента иногда используют понятие средней абсолютной погрешности:

где - модуль абсолютной погрешности в -ом измерении.

Абсолютная погрешность сама по себе не определяет точность измерения. Например, погрешность измерения некоторого вольтметра составляет 0,2 В. Этим вольтметром были произведены измерения напряжения на двух источниках тока: аккумулятора с э.д.с. 36 В и батарейки с э.д.с. 0,5 В. Понятно, что в первом случае измерения будут достаточно точными, а во втором – позволят лишь судить о порядке измеряемой величины.

Относительная погрешность

Относительная погрешность – это отношение абсолютной погрешности измерения к измеренному значению величины:

где - относительная погрешность в -ом измерении.

Относительную погрешность обычно выражают в процентах. Эта погрешность, в отличии от абсолютной, дает некоторое представление о точности измерения, т.к. она сравнивает абсолютную погрешность с измеряемым значением. Например, при измерении напряжения на аккумуляторе (см. выше п. 1.2.1.) относительная погрешность составит %=0,56% , а для батарейки - % =40 %.

Введение