Монотонная функция это кратко

Обновлено: 28.06.2024

Функцию $у = f(x)$ называют возрастающей на промежутке $X$, если для любых двух точек x 1 и x 2 промежутка $X$, таких, что x 1 x 2 , выполняется неравенство f x 1 f x 2 .

Функция является возрастающей, если большему значению независимой переменной соответствует большее значение функции.

Функцию $у = f(x)$ называют убывающей на промежутке $X$, если для любых двух точек x 1 и x 2 промежутка $X$, таких, что x 1 x 2 , выполняется неравенство f x 1 > f x 2 .

Функция является убывающей, если большему значению независимой переменной сопоставимо меньшее значение функции.

Исследование функции на монотонность — одна из важнейших задач в алгебре. В интернете на эту тему много информации, однако она не систематизирована. Некоторые источники не проверены и содержат ошибки и недочеты. Кроме того, часто приводятся неверные примеры решения задач. Для выполнения такой операции следует изучить теорию, а затем приступать к практике.

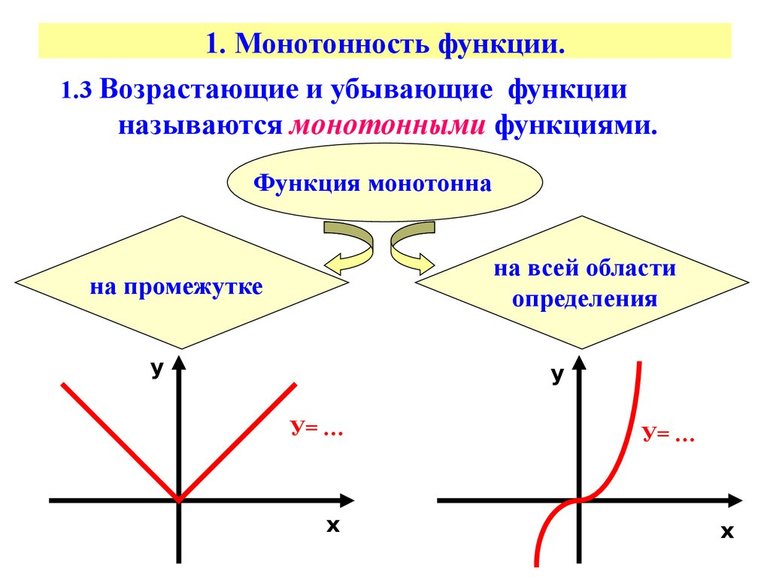
Общие сведения

Функцией вида р = f(r) называется зависимость ее значения от переменной величины "r" или аргумента. Функциональные тождества бывают простыми и сложными. К первым относится класс выражений, состоящих из одной переменной простого типа. Во втором случае содержится несколько аргументов или аргумент является также функцией, т. е. подчиняется определенному закону.

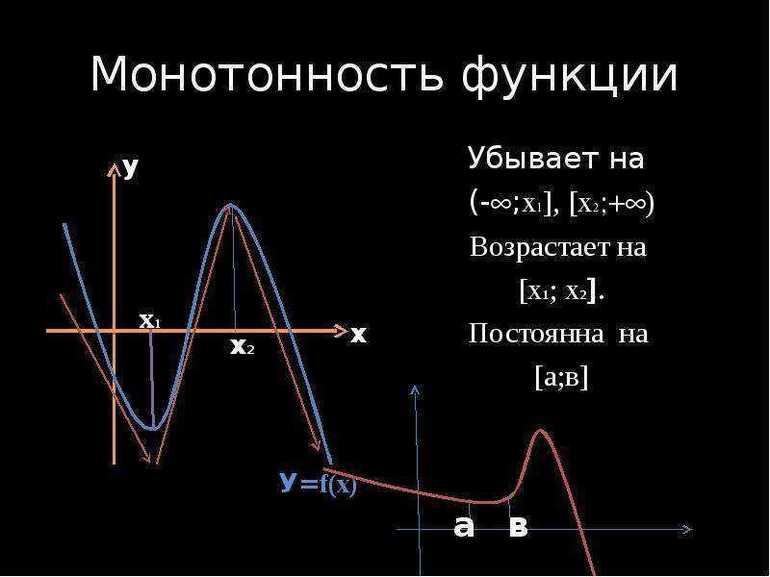
Возрастающая: ∀ r1, r2 ∈ (a;b): r1 r2 ⇒ f(r1) >= f(r2).
Строго убывающая: ∀ r1, r2 ∈ (a;b): r1 > r2 ⇒ f(r1) > f(r2).

Следует отметить, что промежутками монотонности функции называются интервалы, на которых она возрастает или убывает. После определений необходимо рассмотреть основные теоремы, позволяющие использовать соотношения для решения различных задач.

Теорема о пределе

Теорема о пределе монотонной функции применяется для решения задач по высшей математике с использованием пределов. Ее формулировка следующая: если функция вида р = f(r) является дифференцируемой и монотонной на интервале (а;b), то в точке r0, принадлежащей заданному интервалу, она имеет конечные пределы с левой и правой стороны, а в точках r0 = a и r0 = b у нее существуют правосторонние и левосторонние границы.

Чтобы понять математические обозначения sup и inf, необходимо представить множество значений функции. Первый термин обозначает максимальное значение сверху, а второй — минимальное снизу.

Критерии возрастания и убывания

Существуют определенные признаки, по которым можно определить монотонность функции p = f(r) на некотором интервале (а;b). Для этого в математике есть еще три теоремы:

Для убывающей и возрастающей.
Если является строго убывающей или строго возрастающей.
Определение по точке, производной и интервалу.

Первая теорема имеет такую формулировку: дифференцируемая функция p = f(r) на интервале (а;b) является убывающей, когда выполняется неравенство f'(r) = 0 соответственно (при r ∈ данному интервалу).

Формулировка следующего утверждения только для строго возрастающей монотонной функции. В первом случае должно выполняться не одно, а два условия: f'(r) > 0 и f'(r) тождественно не эквивалентна нулю на промежутке в любой точке, принадлежащей интервалу. Для строго убывающей условия немного отличаются от предыдущих: f'(r) 0.

Основные свойства

Для функций на интервале (а;b) существуют некоторые утверждения, позволяющие исследовать составные выражения, а также решать различные задачи. К свойствам монотонных функций относятся следующие:

Сумма двух убывающих (возрастающих) k = f(t) и l = f(v) является возрастающим (убывающим) выражением.
Если k = f(t) возрастает, то -k = f(t) (противоположная) будет убывать. При убывании первой вторая будет возрастать соответственно.
Когда у k = f(t) есть обратная вида k2 = 1 / f(t), тогда при убывании первой вторая будет возрастать. Если первая возрастает, то вторая убывает.
Результатом произведения двух убывающих (возрастающих) является убывающая функция. Также должны выполняться такие условия: k = f(t) >= 0 и l = f(v) >= 0.
Если k = f(t) возрастает или убывает на (а;b), а l = f(t) возрастает или убывает на (c;d), и (а;b) входит в (c;d), то композиция функций к∘ l (k(l(t))) также возрастает или убывает.

После изучения теорем и основных свойств нужно определить минимум базовых знаний, которые необходимы для исследования на монотонность любого выражения. Кроме того, следует знать графики некоторых функций. Для их построения можно использовать специальные онлайн-калькуляторы и программы, позволяющие выделять результаты разными цветами.

Базовые знания

Для исследования функции на монотонность специалисты рекомендуют руководствоваться некоторыми правилами, которые объединяются в универсальный алгоритм. Он является достаточным для выполнения такого задания и имеет следующий вид:

Найти производную первого порядка - f'(r).
Приравнять выражение, полученное в первом пункте, к 0.
Найти критические точки, решив уравнение во втором пункте.
Определить знак f'(r) на промежутках, полученных в результате разбиения критическими точками. Найти промежутки убывания и возрастания.

Последний пункт следует реализовывать при помощи таблицы. Необходимо строго придерживаться алгоритма, поскольку неверные действия способны существенно повлиять на результат.

Нахождение производной

Для поиска производной необходимо выполнить такие шаги: вынести константу, упростить выражение и воспользоваться таблицей дифференциалов элементарных функций (рис. 1). Первые два элемента считаются подготовительными, поскольку позволяют оптимизировать процесс вычисления. Для упрощения следует применять формулы сокращенного умножения, свойства дробей, разложение на множители и т. д. После приведения выражения к упрощенному виду нужно воспользоваться таблицей производных элементарных функций.

Рисунок 1. Дифференциалы простых выражений.

Однако при решении задач не всегда попадаются простые выражения. Для составных существуют определенные правила:

Сумма: [k(t) + l(t)]' = k'(t) + l'(t).
Разность: [k(t) - l(t)]' = k'(t) - l'(t).
Произведение: [k(t) * l(t)]' = k'(t) * l(t) + l'(t) * k(t).
Частное: [k(t) / l(t)]' = [k'(t) * l(t) - l'(t) * k(t)] / (l(t))^2.
Сложная: [k(l(t))]' = l'(t) * k'(t).

Специалисты рекомендуют для проверки использовать программы, но это не значит, что задачи должны решаться только с помощью онлайн-сервисов и математических пакетов.

Корни уравнений и критические точки

Следующим этапом является решение равенства с неизвестным. Необходимо отметить, что уравнения делятся на следующие виды: линейные, квадратные, кубические, биквадратные, тригонометрические, логарифмические, степенные, показательные и иррациональные.

Первый тип решается по очень простому алгоритму: следует перенести неизвестные в одну часть, а известные — в другую. Для решения квадратного уравнения (aw^2 + bw + c = 0) нужно его упростить, разложить на множители или вычислить дискриминант. Последний вычисляется по следующей формуле: D = b^2 - 4ac. Количество корней зависит от значения D и определяется по таким формулам:

В этой статье мы строго определим понятия возрастающей и убывающей функций. Введем понятие монотонности и строгой монотонности, изучим ее свойства. Научимся применять монотонность для решения неравенств и поиска минимумов и максимумов.

Поведение функций

Начем издалека, с рассуждений, которые приведут нас к теме этой статьи. Надо ведь разобраться, как вообще люди пришли к идее возрастающих и убывающих функций, монотонности и почему.

Функция — правило, ставящее числу x в соответствие какое-то значение y . Зададимся вопросом, а как вообще может меняться функция?

Для проведения измерений нам нужно взять две разные точки x 1 и x 2 . Для удобства возьмем такие точки, чтобы x 1 x 2 , то есть мы как бы переходим от x 1 к x 2 (слева направо). Две точки есть. Теперь найдем все возможные варианты изменения функции для этой пары точек:

f ( x 1 ) f ( x 2 ) — значение функции увеличилось
f ( x 1 ) > f ( x 2 ) — значение функции уменьшилось
f ( x 1 ) = f ( x 2 ) — значение функции не изменилось

Итак, в самом общем смысле на паре точек функция может измениться лишь тремя перечисленными выше способами. Ключевой момент — на паре точек x 1 и x 2 . Но поставленный в начале раздела вопрос более общий — нам нужно классифицировать поведение функции в общем на каком-то промежутке!

Судить о поведении функции на промежутке только по ее изменению на двух точках этого промежутка, конечно, нельзя. На иллюстрации ниже приведен наглядный пример, почему так делать нельзя: для пары точек x 1 , x 2 функция уменьшается, а для пары x 3 , x 4 увеличивается.

Как же тогда быть? А все просто! Нужно смотреть на изменение функции не на конкрентной паре точек, а на всех парах x 1 x 2 промежутка. Тогда, по аналогии со всеми возможными вариантами изменения функции на двух точках, можно выделить все возможные варианты поведения функции на промежутке:

Возрастание (для всех пар увеличивается)
Убывание (для всех пар уменьшается)
Постоянство (для всех пар не меняется)
Хаос (разные пары имеют разное изменение)

Теперь, когда у нас есть общее представление о типах поведения функций, приступим к подробному их анализу. Может, этот тернистый и полный опасностей путь выведет нас к интересным и полезным результатам? (спойлер: выведет)

Возрастающая функция

Функция f ( x ) на промежутке M ⊆ R называется возрастающей или неубывающей, когда для любых двух чисел x 1 , x 2 ∈ M этого промежутка, таких, что x 1 x 2 , выполняется неравенство f ( x 1 ) ≤ f ( x 2 ) .

∀ x 1 , x 2 ∈ M : x 1 x 2 ⇒ f ( x 1 ) ≤ f ( x 2 )

Функция f ( x ) на промежутке M ⊆ R называется строго возрастающей, когда для любых двух чисел x 1 , x 2 ∈ M этого промежутка, таких, что x 1 x 2 , выполняется неравенство f ( x 1 ) f ( x 2 ) .

∀ x 1 , x 2 ∈ M : x 1 x 2 ⇒ f ( x 1 ) f ( x 2 )

Выяснить, являются ли следующие функции неубывающими или строго возрастающими: а ) f ( x ) = x б ) f ( x ) = 2 в ) f ( x ) = x 2 г ) f ( x ) = x

Пункт а) Берем две произвольные точки x 1 и x 2 , такие что x 1 x 2 . Раз f ( x ) = x , то получаем следующую ситуацию:

x 1 = f ( x 1 ) x 2 = f ( x 2 )

f ( x 1 ) f ( x 2 )

Это по определению означает, что функция f ( x ) = x является строго возрастающей на всей своей области определения ( − ∞ , + ∞ ) .

Пункт б) Функция f ( x ) = 2 при любом x равна 2 . Значит, для любых пар x 1 и x 2 вида x 1 x 2 значения функции будут равны:

f ( x 1 ) = f ( x 2 ) = 2

Это по определению означает, что функция f ( x ) = 2 неубывает на всей области определения ( − ∞ , + ∞ ) .

Пункт в) Представляем график обычной параболы и замечаем, что функция x 2 не является возрастающей на всей своей области определения. Для доказательства этого достаточно взять x 1 = − 1 и x 2 = 0 . Найдем значения функции для этих точек:

f ( x 1 ) = x 1 2 = ( − 1 ) 2 = 1 f ( x 2 ) = x 2 2 = 0 2 = 0 f ( x 1 ) > f ( x 2 )

Итак, мы нашли такую пару точек, при которых значение функции уменьшилось. Значит, нельзя говорить, что f ( x ) = x 2 является неубывающей или строго возрастающей функцией на всей своей области определения ( − ∞ , + ∞ ) .

Попробуем для этой же функции рассмотреть только неотрицательные x . Вновь возьмем произвольную пару уже неотрицательных чисел 0 ≤ x 1 x 2 . Попробуем доказать, что:

f ( x 1 ) f ( x 2 ) x 1 2 x 2 2 0 x 2 2 − x 1 2 0 ( x 2 − x 1 ) ( x 2 + x 1 )

Первая скобка x 2 − x 1 будет положительной, так как по условию x 1 x 2 . Вторая скобка всегда положительная, так как в ней находится сумма двух положительных чисел. Произведение двух положительных чисел есть число положительное, поэтому последнее неравенство выполняется.

Итак, мы по определению доказали, что квадратичная функция x 2 строго возрастает на полуинтервале [ 0 , + ∞ ) .

Пункт г) Сразу напомню, что квадратный корень от отрицательных чисел мы взять не можем, поэтому областью определения функции x

является все неотрицательные числа, то есть [ 0 , + ∞ ) . Берем две произвольные точки x 1 x 2 из этой области. Для строгой монотонности нам нужно доказать, что

f ( x 1 ) f ( x 2 ) x 1

Выпишем последнее неравенство дважды. В первом обе части умножим на x 1

Моното́нная фу́нкция — это функция, приращение которой не меняет знака, то есть либо всегда неотрицательное, либо всегда неположительное. Если в дополнение приращение не равно нулю, то функция называется стро́го моното́нной. Монотонная функция — это функция, меняющаяся в одном и том же направлении.

Функция возрастает, если большему значению аргумента соответствует большее значение функции. Функция убывает, если большему значению аргумента соответствует меньшее значение функции.

Содержание

Определения

$f:M \subset \R \to \R.$

Пусть дана функция Тогда

(Строго) возрастающая или убывающая функция называется (строго) монотонной.

Другая терминология

Иногда возрастающие функции называют неубыва́ющими, а убывающие функции невозраста́ющими. Строго возрастающие функции тогда зовут просто возрастающими, а строго убывающие просто убывающими.

Свойства монотонных функций

Монотонная функция, определённая на интервале, измерима относительно борелевских сигма-алгебр.
Монотонная функция, определённая на замкнутом интервале, ограничена. В частности, она интегрируема поЛебегу.
Монотонная функция может иметь разрывы только первого рода. В частности, множество точек разрыва не более чем счётно.
Монотонная функция дифференцируемапочти всюду относительно меры Лебега.

Условия монотонности функции

Обратное, вообще говоря, неверно. Производная строго монотонной функции может обращаться в ноль. Однако, множество точек, где производная не равна нулю, должно быть плотно на интервале Точнее имеет место

Аналогично, строго убывает на интервале тогда и только тогда, когда выполнены следующие два условия:

Примеры

См. также

Функции
Элементарная математика
Математический анализ

Wikimedia Foundation . 2010 .

Полезное

Смотреть что такое "Монотонная функция" в других словарях:

Монотонная функция — [monotonic function] — функция f(x), которая может быть либо возрастающей на некотором промежутке (то есть, чем больше любое значение аргумента на этом промежутке, тем больше значение функции), либо убывающей (в противоположном случае).… … Экономико-математический словарь

МОНОТОННАЯ ФУНКЦИЯ — функция, которая при возрастании аргумента либо всегда возрастает (или хотя бы не убывает), либо всегда убывает (не возрастает) … Большой Энциклопедический словарь

МОНОТОННАЯ ФУНКЦИЯ — (monotonie function) Функция, в которой по мере роста значения аргумента значение функции всегда изменяется в том же направлении. Следовательно, если у=f(x), то либо dy/dx > 0 для всех значений х, и в этом случае у является возрастающей… … Экономический словарь

Монотонная функция — (от греч. monótonos однотонный) функция, приращения которой Δf(x) = f(x’) f(x) при Δx = x’ x > 0 не меняют знака, т. е. либо всегда неотрицательны, либо всегда неположительны. Выражаясь не совсем точно, М. ф. это функции, меняющиеся в… … Большая советская энциклопедия

монотонная функция — функция, которая при возрастании аргумента либо всегда возрастает (или хотя бы не убывает), либо всегда убывает (не возрастает). * * * МОНОТОННАЯ ФУНКЦИЯ МОНОТОННАЯ ФУНКЦИЯ, функция, которая при возрастании аргумента либо всегда возрастает (или… … Энциклопедический словарь

МОНОТОННАЯ ФУНКЦИЯ — функция одного переменного, определенная на нек ром подмножестве действительных чисел, приращение к рой при не меняет знака, т. е. либо всегда неотрицательно, либо всегда неположительно. Если строго больше (меньше) нуля, когда то М. ф. наз.… … Математическая энциклопедия

МОНОТОННАЯ ФУНКЦИЯ — функция, к рая при возрастании аргумента либо всегда возрастает (или хотя бы не убывает), либо всегда убывает (не возрастает) … Естествознание. Энциклопедический словарь

Монотонная последовательность — это последовательность, элементы которой с увеличением номера не убывают, или, наоборот, не возрастают. Подобные последовательности часто встречаются при исследованиях и имеют ряд отличительных особенностей и дополнительных свойств.… … Википедия

функция — Команда или группа людей, а также инструментарий или другие ресурсы, которые они используют для выполнения одного или нескольких процессов или деятельности. Например, служба поддержки пользователей. Этот термин также имеет другое значение:… … Справочник технического переводчика

Функция — [function] 1. Зависимая переменная величина; 2. Соответствие y=f(x) между переменными величинами, в силу которого каждому рассматриваемому значению некоторой величины x (аргумента или независимой переменной) соответствует определенное значение… … Экономико-математический словарь

Читайте также: