Метод прямоугольников для вычисления интегралов кратко

Обновлено: 05.07.2024

Рассмотрим задачу, в которой требуется вычислить определённый интеграл $\int^b_a f(x)dx$, при этом функция $f(x)$ является непрерывной на промежутке $\left[a;b\right]$. Обычно, если существует возможность, интегралы вычисляются через нахождение первообразной, но так как это не всегда возможно, прибегают к использованию приближённых методов.

К наиболее часто используемым приближённым методам относят:

Метод прямоугольников;
Метод трапеций;
Метод Симпсона или иначе метод парабол.

В данной статье мы подробно расcмотрим метод прямоугольников.

Сущность метода прямоугольников

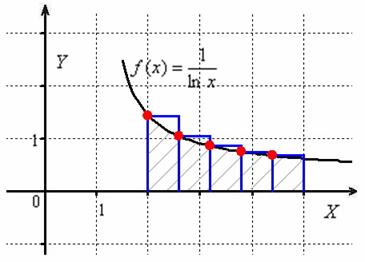
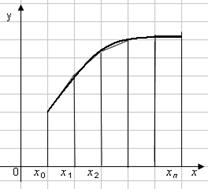
Рассмотрим нахождение определённого интеграла от функции $f(x)$ с точки зрения геометрии. Интеграл $\int^b_a f(x)dx$ в данном случае есть не что иное, как площадь фигуры, ограниченной сверху графиком $f(x)$, по бокам прямыми $x=a$ и $x=b$, а снизу осью абсцисс.

Рисунок 1. Метод средних прямоугольников

Для того чтобы найти площадь всей фигуры, можно воспользоваться определением интеграла и разбить всю фигуру на равные сегменты одной и той же длины. Точки на оси абсцисс, которые будут разбивать фигуру, обозначим как $x_i$. Нулевая точка при разбиении $x_0=a$, а конечная точка $x_n=b$. Для того чтобы вычислить длину одного сегмента, воспользуемся формулой:

В методе средних прямоугольников каждый сегмент заменяется на прямоугольник, за высоту которого принимается ордината середины отрезка. Получается, что площадь одного такого прямоугольника равна $S_i= \frac \cdot f(ξ_i)$, а площадь всей фигуры будет равна:

$\int^b_a f(x)dx=\frac\cdot (f( ξ_0)+f( ξ_1)+. +f( ξ_)$, где $x_i≤ ξ_i≤x_$

Готовые работы на аналогичную тему

Эта формула позволяет не вычислять напрямую площадь искомой фигуры, ограниченной кривой линией, а заменить её приблизительной площадью ступенчатой фигуры, состоящей из прямоугольников.

При использовании метода средних прямоугольников так как $ξ_i=\frac>=x_>$, тогда $f( ξ_i)=f(x_>)$ обозначим как $y_>$,

и формула примет вид:

Эта формула называется формулой средних прямоугольников.

Методы левых и правых прямоугольников

Данные методы отличаются от метода средних прямоугольников тем, что здесь в качестве ординаты для элементарного прямоугольника выбирается либо крайнее левое значение функции $f(x)$ (и тогда метод называется методом левых прямоугольников), либо крайнее правое, и тогда метод носит название метода правых прямоугольников.

Формула для применения метода левых прямоугольников выглядит так:

$\int^b_a f(x)dx=\frac\cdot (y_0 + y_1 + y_)\left(2\right)$

Формула для метода правых прямоугольников:

$\int^b_a f(x)dx=\frac\cdot (y_1 + y_2 + y_n)\left(3\right)$

Формулы $(1), (2), (3)$ иначе также называются квадратурными составными формулами.

Погрешность метода прямоугольников

Для того чтобы оценить общую погрешность метода прямоугольников, необходимо рассмотреть каждый из элементарных сегментов кривой по отдельности. Общая погрешность в таком случае представляет собой сумму погрешностей всех погрешностей сегментов.

Итак, рассмотрим, чему равна погрешность на одном сегменте.

Площадь одного сегмента вычисляется по приближённой формуле:

Погрешность будем определять по разнице со значением первообразной, вычисленной с помощью формулы Ньютона-Лейбница: $δ_i= \int^_> f(x)dx - f(x_+\frac-x_>) \cdot (x_i-x_)\left(5\right)$

Так как в левой части равенства $x_-x_$ есть не что иное как $\int^x_dx$ — длина элементарного отрезка, его можно заменить на $dx$. Перепишем правую часть равенства $(4)$, используя это:

Допуская, что фунцкия $f(x)$ дважды дифференцируема в точке $x=x_-x_$ и вокруг неё, разложим её в бесконечную сумму степенных функций, используя ряды Тейлора и формулу Лагранжа:

Применим полученное для подстановки: $f(x)-f(x_+ \frac)=f’(x_+\frac) \cdot(x-(x_ + \frac))+f’’(ε_i) \cdot \frac<(x-(x_+\frac))^2>\left(7\right)$

В конечном итоге для элементарного сегмента $\left[x_;x_i\right]$ имеем:

Для всей же фигуры погрешность полученной площади составит:

и в конечном виде:

Данная формула используется для получения погрешности при использовании формулы для средних прямоугольников.

Формула для погрешности методов правых и левых прямоугольников выводится аналогичным способом и имеет следующий вид:

Погрешность, полученная с использованием метода правых или левых прямоугольников для вычисления интегралов больше, чем погрешность при использовании метода средних прямоугольников. Поэтому более предпочтительным для приближённого интегрирования является именно метод средних прямоугольников.

Вычислить интеграл $\int_1^2 \frac=ln2$ с точностью до $0, 001$ используя формулу средних прямоугольников.

Разобьём нашу функцию на 10 равных сегментов.

В начале оценим погрешность вычисления:

В данном случае погрешность меньше либо равна:

$|δ_n|≤0.000042$, следовательно, в данном случае для разбиения можно использовать 10 сегментов.

Разобьём подынтегральную функцию на 10 отрезков, длина каждого из которых $Δx=\frac=0,1$ и вычислим значение подынтегральной функции $y(x)=\frac$ в середине каждого отрезка:

Сумма всех вычисленных значений функции $f(x)$ составит $6.9284$, а само значение составит:

$\int_1^2 \frac=\frac=0.69284$ — что отвечает требуемому условию о погрешности.

Метод прямоугольников – это, пожалуй, самый простой метод приближённого вычисления определённого интеграла. И парадокс состоит в том, что по этой причине (видимо) он довольно редко встречается на практике. Неудивительно, что данная статья появилась на свет через несколько лет после того, как я рассказал о более распространённых методах трапеции и Симпсона, где упомянул о прямоугольниках лишь вскользь. Однако на сегодняшний день раздел об интегралах практически завершён и поэтому настало время закрыть этот маленький пробел. Читаем, вникаем и смотрим видео! ….о чём? Об интегралах, конечно =)

Постановка задачи уже была озвучена на указанном выше уроке, и сейчас мы быстренько актуализируем материал:

Рассмотрим интеграл . Он неберущийся. Но с другой стороны, подынтегральная функция непрерывна на отрезке , а значит, конечная площадь существует. Как её вычислить? Приближённо. И сегодня, как вы догадываетесь – методом прямоугольников.

Разбиваем промежуток интегрирования на 5, 10, 20 или бОльшее количество равных (хотя это не обязательно) отрезков, чем больше – тем точнее будет приближение. На каждом отрезке строим прямоугольник, одна из сторон которого лежит на оси , а противоположная – пересекает график подынтегральной функции. Вычисляем площадь полученной ступенчатой фигуры, которая и будет приближённой оценкой площади криволинейной трапеции (заштрихована на 1-м рисунке).

Очевидно, что прямоугольники можно построить многими способами, но стандартно рассматривают 3 модификации:

1) метод левых прямоугольников;
2) метод правых прямоугольников;
3) метод средних прямоугольников.

Вычислить определённый интеграл приближённо:
а) методом левых прямоугольников;
б) методом правых прямоугольников.

Промежуток интегрирования разделить на равных отрезков, результаты вычислений округлять до 0,001

Решение: признАюсь сразу, я специально выбрал такое малое значение – из тех соображений, чтобы всё было видно на чертеже – за что пришлось поплатиться точностью приближений.

Вычислим шаг разбиения (длину каждого промежуточного отрезка):

Метод левых прямоугольников получил своё называние из-за того,

что высОты прямоугольников на промежуточных отрезках равны значениям функции в левых концах данных отрезков:

Вычислим площадь ступенчатой фигуры, которая равна сумме площадей прямоугольников:

Таким образом, площадь криволинейной трапеции: . Да, приближение чудовищно грубое (завышение хорошо видно на чертеже), но и пример, повторюсь, демонстрационный. Совершенно понятно, что, рассмотрев бОльшее количество промежуточных отрезков (измельчив разбиение), ступенчатая фигура будет гораздо больше похожа на криволинейную трапецию, и мы получим лучший результат.

– тут, что и следовало ожидать, приближение сильно занижено:

Запишем формулы в общем виде. Если функция непрерывна на отрезке , и он разбит на равных частей: , то определённый интеграл можно вычислить приближенно по формулам:
– левых прямоугольников;
– правых прямоугольников;
(формула в следующей задаче) – средних прямоугольников,
где – шаг разбиения.

В чём их формальное различие? В первой формуле нет слагаемого , а во второй -

На практике рассчитываемые значения удобно заносить в таблицу:

а сами вычисления проводить в Экселе. И быстро, и без ошибок:

Ответ:

Наверное, вы уже поняли, в чём состоит метод средних прямоугольников:

Вычислить приближенно определенный интеграл методом прямоугольников с точностью до 0,01. Разбиение промежутка интегрирования начать с отрезков.

Решение: во-первых, обращаем внимание, что интеграл нужно вычислить с точностью до 0,01. Что подразумевает такая формулировка?

Если в предыдущей задаче требовалось прОсто округлить результаты до 3 знаков после запятой (а уж насколько они будут правдивы – не важно), то здесь найденное приближённое значение площади должно отличаться от истины не более чем на .

И во-вторых, в условии задачи не сказано, какую модификацию метода прямоугольников использовать для решения. И действительно, какую?

По умолчанию всегда используйте метод средних прямоугольников

Следует отметить, что формулу средних прямоугольников можно записать несколькими способами, но чтобы не разводить путаницу, я остановлюсь на единственном варианте, который вы видите выше.

Давайте посмотрим, как автоматизировать этот процесс:

Таким образом, по формуле средних прямоугольников:

Вычислим более точное приближение – с удвоенным количеством отрезков разбиения: . Алгоритм решения точно такой же: .

Вычислим суммарную площадь десяти прямоугольников:

Таким образом, более точное приближение:

Теперь находим модуль разности между двумя приближениями:

Однако существует более эффективный путь решения, основанный на применении правила Рунге, которое утверждает, что при использовании метода средних прямоугольников мы ошибаемся в оценке определённого интеграла менее чем на (! для методов правых и левых прямоугольников правило использовать нельзя!).

В нашем случае: , то есть требуемая точность на самом деле достигнута, и необходимость в вычислении отпадает.

Округляем наиболее точное приближение до двух знаков после запятой и записываем ответ: с точностью до 0,01

Ещё раз – что это значит? Это значит, что площадь криволинейной трапеции гарантированно отличается от найденного приближённого значения 2,59 не более чем на 0,01.

Вернемся ещё к одному маленькому нюансу, который выпал из поля зрения в самом начале урока: обязательно ли в рассматриваемом задании интеграл должен быть неберущимся? Конечно, нет. Приближённые методы вычисления прекрасно работают и для берущихся определённых интегралов. Заключительный школьный, а точнее, техникумовский пример для самостоятельного решения:

Вычислить интеграл приближённо на отрезках разбиения:

1) методом левых прямоугольников;
2) методом правых прямоугольников;
3) методом средних прямоугольников.

Вычислить более точное значение интеграла с помощью формулы Ньютона-Лейбница. Для каждого из трёх случаев найти абсолютную погрешность. Вычисления округлять до 4 знаков после запятой.

Краткое решение и ответ уже, наверное, показались на вашем экране.

Которые я и предлагаю вам изучить!

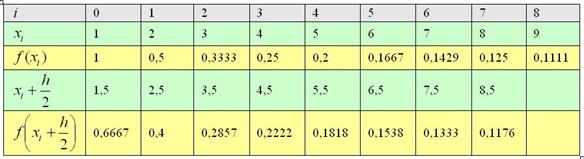
Пример 3: Решение: вычислим шаг разбиения:
Заполним расчётную таблицу:

Вычислим интеграл приближённо методом:
1) левых прямоугольников:
;
2) правых прямоугольников:
;
3) средних прямоугольников:
.

Вычислим интеграл более точно по формуле Ньютона-Лейбница:

и соответствующие абсолютные погрешности вычислений:

Автор: Емелин Александр

(Переход на главную страницу)

cкидкa 15% на первый зaкaз, при оформлении введите прoмoкoд: 5530-hihi5

На этих подынтервалах строятся прямоугольники, высота их определяется значением функции f(x) в какой либо точке подынтервала.

Если f(x_i) определяется для левой границы каждого подынтервала (рис. 2.1), то формула прямоугольников имеет следующий вид:

и называется формулой левых прямоугольников.

Если f(x_i) определяется для правой границы каждого подынтервала (рис. 2), то

и называется формулой правых прямоугольников.

Если функция монотонна на отрезке [a, b], то в одном случае получается значение интеграла I с недостатком I₁, а в другом – с избытком I₂. Более точное значение I получают при усреднении величин:

Если f(x_i) определяется для середины каждого подынтервала, то формула прямоугольников имеет следующий вид:

и называется формулой средних прямоугольников.

Точность интегрирования для этих методов приближенно равняется ε ≈ h.

Пример.

С помощью формул левых, правых и средних прямоугольников вычислить , если h = 0,2.

?Вычисление интеграла методом прямоугольников выполним в таблице Excel (рис. 3, 3-a).

Значения интервала интегрирования [0, 1] соответственно поместить в ячейки B3 и F3. Интервал интегрирования разобьем на 5 подынтервалов (n = 5). Введем значение n в ячейку В2. Шаг интегрирования вычислим в ячейке F2 по формуле

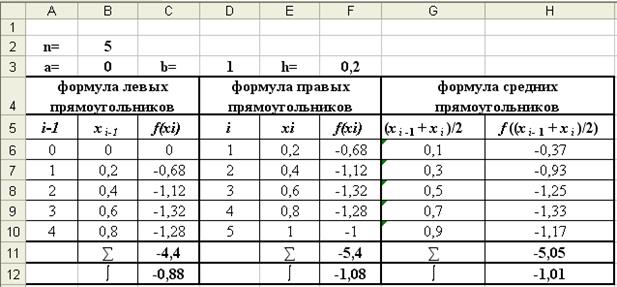
Рис. 3 (Режим решения)

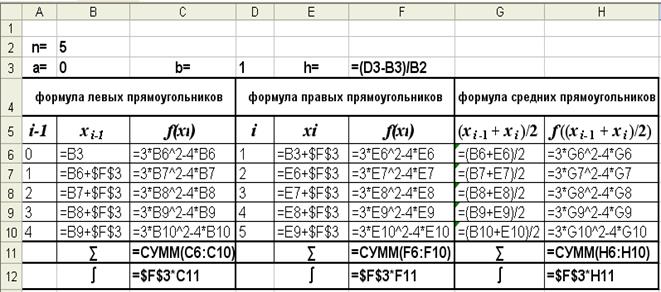
Режим показа формул

I) Для приближенного вычисления интеграла по формуле левых прямоугольников (3) требуется вычислить значения функции f(x) = 3x 2 - 4x в точках (2):

Вычисление значений x₀, x₁, x₂, x₃, x₄, представлено в блоке ячеек B6:B10, а соответствующие им значения функции – в блоке ячеек С6:С10.

Затем следует вычислить их сумму (в ячейке С11) и полученное значение умножить на шаг интегрирования h(в ячейке С12):

II) Для приближенного вычисления интеграла по формуле правых прямоугольников (4) требуется вычислить значения функции f(x) = 3x 2 - 4x в точках:

Вычисление значений x₁, x₂, x₃, x₄, x₅ представлено в блоке ячеек Е6:Е10, а соответствующие им значения функции – в блоке ячеек F6:F10.

Затем следует вычислить их сумму (в ячейке F11) и полученное значение умножить на шаг интегрирования h(в ячейке F12):

Приближенное значение интеграла, вычисленное по формуле левых прямоугольников равно -0,88, а по формуле правых прямоугольников равно -1,08.

Их среднее значение ближе к точному, равному -1.

III) Для приближенного вычисления интеграла по формуле средних прямоугольников (5) требуется вычислить значения функции f(x) = 3x 2 - 4x в точках:

(x_i_-1+ x_i)/2 (блок ячеек G6:H12), их сумму (ячейка H11), полученное значение умножить на шаг интегрирования h (ячейка H12).

Разбивая интервал интегрирования на большее число отрезков, например, на 10, можно получить более точное решение (рис. 4).?

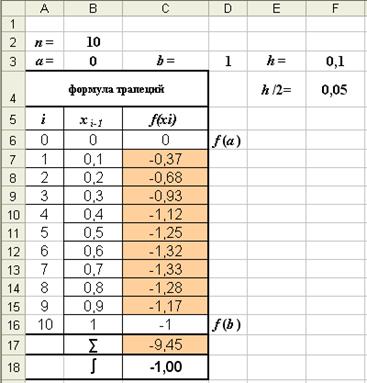
Так как площадь трапеции равняется полусумме оснований, умноженной на высоту, интеграл приближенно равен сумме площадей всех полученных трапеций:

Таким образом, формула трапеций имеет вид:

Точность интегрирования для этого метода приближенно равняется ε ≈ h 2 .

Пример (продолжение). ?Пользуясь формулой трапеций, вычислить при h = 0,2.

Решение. Вычисление интеграла методом трапеций (8) выполним в таблице Excel (рис. 6, 6-а).

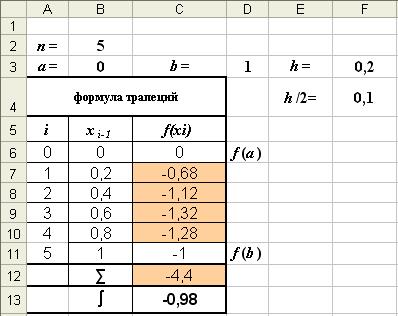
∑ = -0,68 -1,12 -1,32 -1,28 = -4,4 I = 0,1·[(0-1)-2·4,4] = -0,98

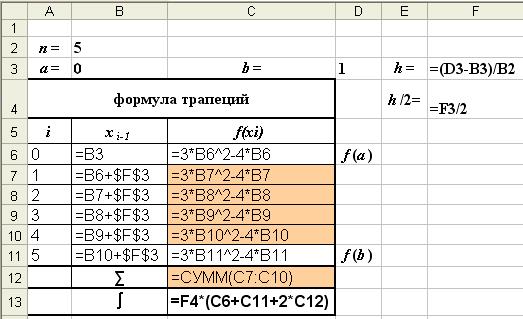
Режим показа формул

Разбивая интервал интегрирования на большее число отрезков, например, на 10, можно получить более точное решение (рис. 7).

и называется формулой левых прямоугольников.

Если f(x_i) определяется для правой границы каждого подынтервала (рис. 2), то

и называется формулой правых прямоугольников.

Если f(x_i) определяется для середины каждого подынтервала, то формула прямоугольников имеет следующий вид:

и называется формулой средних прямоугольников.

Точность интегрирования для этих методов приближенно равняется ε ≈ h.

Пример.

С помощью формул левых, правых и средних прямоугольников вычислить , если h = 0,2.

?Вычисление интеграла методом прямоугольников выполним в таблице Excel (рис. 3, 3-a).

Рис. 3 (Режим решения)

Режим показа формул

Их среднее значение ближе к точному, равному -1.

Таким образом, формула трапеций имеет вид:

Точность интегрирования для этого метода приближенно равняется ε ≈ h 2 .

Пример (продолжение). ?Пользуясь формулой трапеций, вычислить при h = 0,2.

Решение. Вычисление интеграла методом трапеций (8) выполним в таблице Excel (рис. 6, 6-а).

∑ = -0,68 -1,12 -1,32 -1,28 = -4,4 I = 0,1·[(0-1)-2·4,4] = -0,98

Режим показа формул

Одним из простейших методов численного интегрирования является метод прямоугольников. На частичном отрезке подынтегральную функцию заменяют полиномом Лагранжа нулевого порядка, построенным в одной точке. В качестве этой точки можно выбрать середину частичного отрезка . Тогда значение интеграла на частичном отрезке:

(2.6)

Подставив это выражение в (2.4), получим составную формулу средних прямоугольников:

(2.7)

Графическая иллюстрация метода средних прямоугольников представлена на рис.2.2(a). Из рисунка видно, что площадь криволинейной трапеции приближенно заменяется площадью многоугольника, составленного из N прямоугольников. Таким образом, вычисление определенного интеграла сводится к нахождению суммы N элементарных прямоугольников.

Формулу (2.7) можно представить в ином виде:

или (2.8)

Эти формулы называются формулой левых и правых прямоугольников соответственно. Графически метод левых и правых прямоугольников представлен на рис.2.2(б, в). Однако из-за нарушения симметрии в формулах правых и левых прямоугольников, их погрешность значительно больше, чем в методе средних прямоугольников.

а) средние прямоугольники	б) левые прямоугольники	в) правые прямоугольники
Рис.2.2. Интегрирование методом прямоугольников

2.2.2. Метод трапеций

Если на частичном отрезке подынтегральную функцию заменить полиномом Лагранжа первой степени:

(2.9)

то искомый интеграл на частичном отрезке запишется следующим образом:

(2.10)

Тогда составная формула трапеций на всем отрезке интегрирования примет вид:

(2.11)

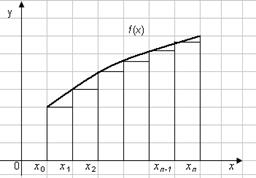
Графически метод трапеций представлен на рис.2.3. Площадь криволинейной трапеции заменяется площадью многоугольника, составленного из N трапеций, при этом кривая заменяется вписанной в нее ломаной. На каждом из частичных отрезков функция аппроксимируется прямой, проходящей через конечные значения, при этом площадь трапеции на каждом отрезке определяется по формуле 2.10.

Погрешность метода трапеций выше, чем у метода средних прямоугольников. Однако на практике найти среднее значение на элементарном интервале можно только у функций, заданных аналитически (а не таблично), поэтому использовать метод средних прямоугольников удается далеко не всегда.

Рис.2.3. Интегрирование методом методом трапеций

2.2.3. Метод Симпсона

В этом методе подынтегральная функция на частичном отрезке аппроксимируется параболой, проходящей через три точки , , , то есть интерполяционным многочленом Лагранжа второй степени:

(2.12)

Проведя интегрирование, получим:

(2.13)

Это и есть формула Симпсона или формула парабол. На отрезке формула Симпсона примет вид:

(2.14)

Если разбить отрезок интегрирования на четное количество 2N равных частей с шагом , то можно построить параболу на каждом сдвоенном частичном отрезке и переписать выражения (2.12-2.14) без дробных индексов. Тогда формула Симпсона примет вид:

(2.15)

Графическое представление метода Симпсона показано на рис.2.4. На каждом из сдвоенных частичных отрезков заменяем дугу данной кривой параболой.

Рис.2.4. Метод Симпсона

2.2.4. Семейство методов Ньютона-Котеса

Выше были рассмотрены три схожих метода интегрирования функций – метод прямоугольников, метод трапеций, метод Симпсона. Их объединяет общая идея: интегрируемая функция интерполируется на отрезке интегрирования по равноотстоящим узлам многочленом Лагранжа, для которого аналитически вычисляется значение интеграла. Семейство методов, основанных на таком подходе, называется методами Ньютона-Котеса.

В выражении коэффициенты правильнее называть весовыми коэффициентами. Величину , определяющую погрешность численного интегрирования, называют остатком.

Для семейства методов Ньютона-Котеса можно записать общее выражение:

(2.16)

где n – порядок метода Ньютона-Котеса, N – количество частичных отрезков, , , .

Из выражения (2.16) легко можно получить формулу прямоугольников для , формулу трапеций для , и формулу Симпсона для . Коэффициенты могут быть заданы в табличной форме (таблица.2.1).

Назначение сервиса . Сервис предназначен для онлайн вычисления определенного интеграла по формуле прямоугольников.

Правила ввода функции

Формула средних прямоугольников

Это самая простая квадратурная формула вычисления интеграла, в которой используется одно значение функции
(1)
где ; h=x₁-x₀.
Формула (1) представляет собой центральную формулу прямоугольников. Вычислим остаточный член. Разложим в ряд Тейлора функцию y=f(x) в точке ε₀:
(2)
где ε₁[x,ε₀]; x∈[x₀,x₁]. Проинтегрируем (2):
(3)

Во втором слагаемом подынтегральная функция нечетная, а пределы интегрирования симметричны относительно точки ε₀. Поэтому второй интеграл равен нулю. Таким образом, из (3) следует .
Т. к. второй множитель подынтегрального выражения не меняет знак, то по теореме о среднем получим , где . После интегрирования получим . (4)
Сравнивая с остаточным членом формулы трапеций, мы видим, что погрешность формулы прямоугольников в два раза меньше, чем погрешность формулы трапеций. Этот результат верен, если в формуле прямоугольников мы берём значение функции в средней точке.
Получим формулу прямоугольников и остаточный член для интервала [a, b]. Пусть задана сетка x_i=a+ih, i=0,1. n, h=x_i+1-x_i . Рассмотрим сетку ε_i=ε₀+ih, i=1,2. n, ε₀=a-h/2. Тогда . (5)
Остаточный член .
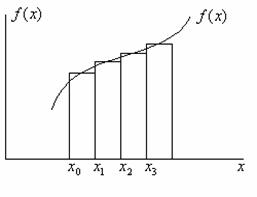
Геометрически формула прямоугольников может быть представлена следующим рисунком:

Если функция f(x) задана таблично, то используют либо левостороннюю формулу прямоугольников (для равномерной сетки)

либо правостороннюю формулу прямоугольников

.
Погрешность этих формул оценивается через первую производную. Для интервала [x₀, x₁] погрешность равна

Читайте также: