Метод контурных токов кратко

Обновлено: 02.07.2024

Ме́тод ко́нтурных то́ков — метод сокращения размерности системы уравнений, описывающей электрическую цепь.

Содержание

Основные принципы

Любая электрическая цепь, состоящая из Р рёбер (ветвей, участков, звеньев) и У узлов, может быть описана системой уравнений в соответствии с 1-м и 2-м правилами Кирхгофа. Число уравнений в такой системе равно Р, из них У–1 уравнений составляется по 1-му закону Кирхгофа для всех узлов, кроме одного; а остальные Р–У+1 уравнений – по 2-му закону Кирхгофа для всех независимых контуров. Поскольку независимыми переменными в цепи считаются токи рёбер, число независимых переменных равно числу уравнений, и система разрешима.

Существует несколько методов сократить число уравнений в системе. Одним из таких методов является метод контурных токов.

Метод использует тот факт, что не все токи в рёбрах цепи являются независимыми. Наличие в системе У–1 уравнений для узлов означает, что зависимы У–1 токов. Если выделить в цепи Р–У+1 независимых токов, то систему можно сократить до Р–У+1 уравнений. Метод контурных токов основан на очень простом и удобном способе выделения в цепи Р–У+1 независимых токов.

Метод контурных токов основан на допущении, что в каждом из Р–У+1 независимых контуров схемы циркулирует некоторый виртуальный контурный ток. Если некоторое ребро принадлежит только одному контуру, реальный ток в нём равен контурному. Если же ребро принадлежит нескольким контурам, ток в нём равен сумме соответствующих контурных токов (с учётом направления обхода контуров). Поскольку независимые контура покрывают собой всю схему (т.е. любое ребро принадлежит хотя бы одному контуру), то ток в любом ребре можно выразить через контурные токи, и контурные токи составляют полную систему токов.

Построение системы контуров

Использование планарных графов

Наиболее простым и наглядным методом построения системы независимых контуров является построение планарного графа схемы, то есть размещение ветвей и узлов цепи на плоскости без взаимных пересечений рёбер. Планарный граф разбивает плоскость на К ограниченных областей. Можно показать, что замкнутые цепочки рёбер, ограничивающие эти области, являются системой независимых контуров для рассматриваемой схемы.

Метод планарного графа предпочтителен при ручном расчёте схем. В случае, если схему невозможно изобразить в виде планарного графа, а также в случае компьютерного построения системы контуров, применение этого метода может оказаться невозможным.

Метод выделения максимального дерева

Дерево представляет собой подмножество звеньев цепи, представляющее собой односвязный (то есть состоящий из одной части) граф, в котором нет замкнутых контуров. Дерево получается из цепи путём исключения из него некоторых звеньев. Максимальное дерево - это дерево, для которого добавление к нему любого исключённого звена приводит к образованию контура.

Метод выделения максимального дерева основан на последовательном исключении из цепи определённых звеньев согласно следующим правилам:

В конце работы алгоритма число исключённых из цепи звеньев оказывается точно равно числу независимых контуров схемы. Каждый независимый контур получается присоединением к цепи соответствующего исключённого звена.

Пример выделения максимального дерева

Удаление звена R1

Удаление звеньев R2 и R3

Присоединение к дереву удалённого звена образует контур

Построение системы уравнений

Для построения системы уравнений необходимо выделить в цепи P – У + 1 независимых контуров. По каждому из этих контуров будет составлено одно уравнение по 2-му закону Кирхгофа. В каждом контуре необходимо выбрать направление обхода (например, по часовой стрелке).

Выделение независимых контуров можно осуществить одним из перечисленных выше методов. Следует отметить, что система независимых контуров, как правило, не единственна, как не единственно и максимальное дерево цепи. Однако системы уравнений, составленные по различным системам контуров математически эквивалентны, поэтому возможен специальный подбор системы контуров, дающей наиболее простую систему уравнений.

Отметим также, что при любом выборе системы контуров в любом контуре обязательно найдётся ребро, которое входит только в этот контур и ни в какой другой. Таким образом, контурный ток всегда совпадает с током в одном из рёбер этого контура. Например, для схемы, изображённой на рисунке, звено 4 входит только в левый контур, поэтому контурный ток обозначен как I₄. То же самое относится к двум другим контурам, токи в которых обозначены как I₅ и I₆. В литературе встречаются и другие обозначения для контурных токов, например, римскими цифрами (I_I, I_II, I_III . ), латинскими буквами (I_A, I_B, I_C . ) и т. д.

Принцип построения системы уравнений следующий.

Для первого контура (I₄):

Для второго контура (I₅):

Для третьего контура (I₆):

Окончательно получаем систему уравнений

$\begin (Z_1+Z_2+Z_4) \cdot I_4 -Z_2 \cdot I_5 -Z_1 \cdot I_6 = E_4 \\ -Z_2 \cdot I_4 + (Z_2+Z_3+Z_5) \cdot I_5 -Z_3 \cdot I_6 = Z_5J_5 \\ -Z_1 \cdot I_4 -Z_3 \cdot I_5 + (Z_1+Z_3+Z_6) \cdot I_6 = E_6 \end.$

Оптимизированная процедура составления системы

Как видно из вышесказанного, процедуру составления системы можно упростить следующим образом:

В левой части К-го уравнения записываем произведение контурного тока на сумму сопротивлений всех звеньев, входящих в контур:

$\ I_K$

где — ток контура, для которого записывается уравнение;

$\ Z_<K1> . Z_$
— сопротивления звеньев, входящих в этот контур.

От левой части уравнения отнимаем остальные контурные токи, умноженные на суммы сопротивлений звеньев, по которым контур К пересекается с этими контурами:

$\ I_A, I_B, .$

где — токи контуров, пересекающихся с контуром К;

$\ Z_<KA1> , Z_, .$
— сопротивления звеньев, входящих одновременно в контура К и A.

Составив уравнения для всех независимых контуров, получаем совместную систему P–У+1 уравнений относительно P–У+1 неизвестных контурных токов.

Пример

Положим, что в левом контуре по часовой стрелке течет контурный ток I₁₁, а в правом (также по часовой стрелке) — контурный ток I₂₂. Для каждого из контуров составим уравнения по второму закону Кирхгофа. При этом учтем, что по смежной ветви (с сопротивлением R₅) течет сверху вниз ток I₁₁–I₂₂. Направления обхода контуров примем также по часовой стрелке.

Для первого контура

Для второго контура

Перепишем эти уравнения следующим образом:

$\begin R_I_+R_I_=E_\\ R_I_+R_I_=E_\\ \end$

=R_1+R_2+R_5$" width="" height="" />
— полное сопротивление первого контура; =R_3+R_4+R_5$" width="" height="" />
— полное сопротивление второго контура; =R_=-R_5$" width="" height="" />
— сопротивления смежной ветви между первым и вторым контурами, взятые со знаком минус; =E_1+E_5$" width="" height="" />
— контурная ЭДС первого контура; =-E_4-E_5$" width="" height="" />
— контурная ЭДС второго контура.

Формальный подход

В матричном виде система уравнений для метода контурных токов выглядит следующим образом [1] :

$\mathbf<C Z C^t I_2 = C (E+ZJ)> ,$

$\mathbf C$

— матрица контуров размера n × p (где n — количество независимых контуров, р — количество звеньев) , в которой i–я строка соответствует независимому контуру i, а j–й столбец соответствует звену j, причём элемент C_ij равен

0, если ребро j не входит в контур i;
1, если ребро входит в контур и направление ребра соответствует направлению обхода контура;
–1, если ребро входит в контур и направление ребра противоположно направлению обхода контура.

Для каждого ребра задаётся направление, которое обычно ассоциируется с направлением тока в этом ребре;

$\mathbf Z$

— диагональная матрица сопротивлений размера p × p, в которой диагональный элемент Z_ii равен сопротивлению i–го ребра, а недиагональные элементы равны нулю;

$\mathbf C^t$

— транспонированная матрица контуров;

$\mathbf I_2$

— матрица-столбец контурных токов размером n × 1.

$\mathbf J$

— матрица-столбец источников тока размером p × 1, где каждый элемент равен току источника в соответствующем ребре, причём эта величина нулевая, если в данном ребре источник тока отсутствует; положительная, если направление тока источника совпадает с направлением тока в ребре; и отрицательная в противном случае;

$\mathbf E$

— матрица-столбец источников ЭДС размером p × 1, где каждый элемент равен ЭДС источника в соответствующем ребре, причём эта величина нулевая, если в данном ребре источник ЭДС отсутствует; положительная, если направление ЭДС источника совпадает с направлением тока в ребре; и отрицательная в противном случае.

Пример системы уравнений

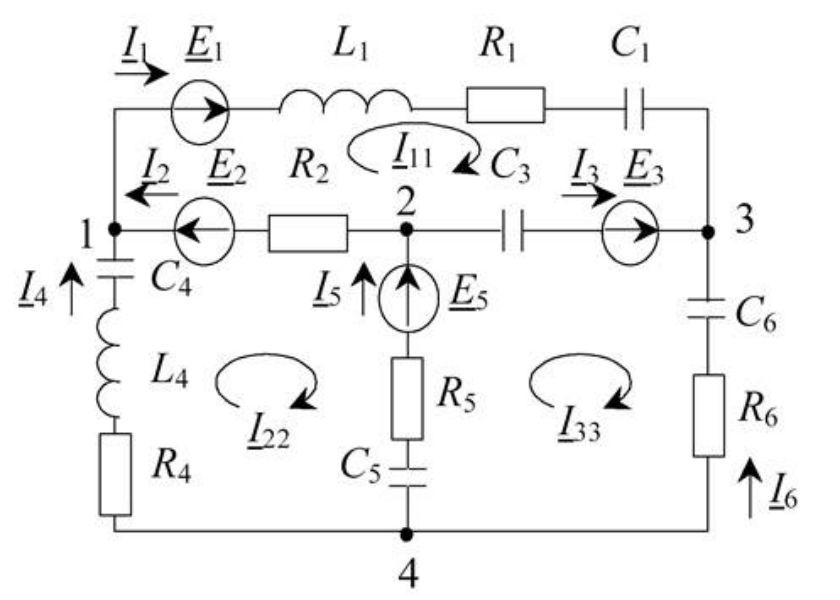
Для схемы рис. 2 матрицы имеют вид:

$\mathbf C = \begin -1 & -1 & 0 & 1 & 0 & 0 \\ 0 & 1 & -1 & 0 & 1 & 0 \\ 1 & 0 & 1 & 0 & 0 & 1 \end; \quad \mathbf I_2 = \begin I_4 \\ I_5 \\ I_6 \end$

$\mathbf C^t = \begin -1&0&1 \\ -1&1&0 \\ 0&-1&1 \\ 1&0&0 \\ 0&1&0 \\ 0&0&1 \\ \end; \quad \mathbf Z = \begin Z_1&0&0&0&0&0 \\ 0&Z_2&0&0&0&0 \\ 0&0&Z_3&0&0&0 \\ 0&0&0&Z_4&0&0 \\ 0&0&0&0&Z_5&0 \\ 0&0&0&0&0&Z_6 \\ \end; \quad \mathbf J = \begin 0 \\ 0 \\ 0 \\ 0 \\ J_5 \\ 0 \end; \quad \mathbf E = \begin 0 \\ 0 \\ 0 \\ E_4 \\ 0 \\ E_6 \end$

Перемножаем матрицы в соответствии с матричным уравнением:

$\mathbf <CZ> = \begin -Z_1 & -Z_2 & 0 & Z_4 & 0 & 0 \\ 0 & Z_2 & -Z_3 & 0 & Z_5 & 0 \\ Z_1 & 0 & Z_3 & 0 & 0 & Z_6 \end;$

$\mathbf <CZC^t> = \begin Z_1+Z_2+Z_4 & -Z_2 & -Z_1 \\ -Z_2 & Z_2+Z_3+Z_5 & -Z_3 \\ -Z_1 & -Z_3 & Z_1+Z_3+Z_6 \end;$

$\mathbf <CZC^tI_2> = \begin (Z_1+Z_2+Z_4) \cdot I_4 -Z_2 \cdot I_5 -Z_1 \cdot I_6 \\ -Z_2 \cdot I_4 + (Z_2+Z_3+Z_5) \cdot I_5 -Z_3 \cdot I_6 \\ -Z_1 \cdot I_4 -Z_3 \cdot I_5 + (Z_1+Z_3+Z_6) \cdot I_6 \end;$

$\mathbf <E+ZJ> = \begin 0 \\ 0 \\ 0 \\ E_4 \\ Z_5J_5 \\ E_6 \end; \quad \mathbf = \begin E_4 \\ Z_5J_5 \\ E_6 \end$

Раскрывая матричную запись, получаем следующую систему уравнений:

$\begin (Z_1+Z_2+Z_4) \cdot I_4 -Z_2 \cdot I_5 -Z_1 \cdot I_6 = E_4 \\ -Z_2 \cdot I_4 + (Z_2+Z_3+Z_5) \cdot I_5 -Z_3 \cdot I_6 = Z_5J_5 \\ -Z_1 \cdot I_4 -Z_3 \cdot I_5 + (Z_1+Z_3+Z_6) \cdot I_6 = E_6 \end.$

Для расчёта величин токов в электрических цепях применяются различные алгоритмы, основанные на базовых принципах: законе Ома и законах Кирхгофа. Метод контурных токов (МКТ) — один из таких алгоритмов, позволяющий уменьшить количество уравнений, решая которые получают искомые значения токов, протекающих в отдельных участках цепи.

Базовые принципы

Рис.1 Графическое представление основных терминов МКТ

Nу -1 для токов (по первому правилу Кирхгофа);
Nр - Nу +1 для напряжений по второму правилу Кирхгофа (ВПК).

Понятно, что чем больше уравнений в системе, тем сложнее и дольше будет длиться процесс её решения. Для облегчения расчетов были предложены алгоритмы, позволяющие существенно уменьшить число уравнений. МКТ является одной из таких методик, использующей (Nр - Nу + 1) уравнений по ВПК, дополненных понятием контурного тока — вспомогательной, гипотетической величиной.

Термины, определения и главная идея МКТ

Для расчетов реальных (действительных) значений токов в МКТ было введено дополнительное понятие о фиктивной (виртуальной) величине, названной контурным током (КТ), протекающим (гипотетически) в каждом независимом контуре. КТ имеет одно и то же значение в ветвях данного контура.

Расчёт действительных токов в электрических цепях с помощью МКТ производится в следующей последовательности:

Способы построения контуров

Тщательное обозначение контуров позволяет задать минимальный набор КТ. Любой элемент схемы должен быть представлен хотя в одном контуре. При построении используются два основных метода:

планарных графов;
выделения максимального дерева.

Применение планарных графов

Выделение максимального дерева

Данный математический метод разработан для компьютерных расчётов с помощью соответствующего программного обеспечения. Основная идея метода состоит в изъятии отдельных ветвей в соответствии с жёстким алгоритмом:

Последовательность формирования системы уравнений

Набор (система) уравнений для нахождения действительных токов ветвей в МКТ строится следующим образом:

Оптимизированная процедура построения системы

В общем виде процедуру построения системы уравнений состоит из следующих этапов:

1. Для N-го контура в левую половину N-го уравнения заносят JN (величина КТ, умноженная на сумму всех сопротивлений данного контура):

где JN — ток контура, RN1, RN2. RNn — сопротивления, присутствующие в данном контуре.

2. Из левой половины уравнения вычитаются прочие КТ, умноженные на суммы сопротивлений, по которым N-й контур имеет пересечения:

. - JA (RNA1 + RNA2 + . ) - JB (RNB1 + RNB2 + . ) - .

где JA, JB — ТК, пересекающиеся с N-ым контуром; RNA1, RNA2 — сопротивления участков, входящих одновременно в контуры N и A.

3. Правая половина уравнения представляет собой сумму ЭДС-источников данного контура:

. ± IA1 RN1 ± IA2 RN2 ± .

Написав уравнения для всех независимых контуров, получим искомую систему (Nр - Nу + 1) уравнений для нахождения такого же числа неизвестных контурных токов.

Формальный подход

Система уравнений для МКТ, записанная в матричном представлении, называется формальным подходом. Для расчётов необходимы следующие матрицы:

С — состоит из i строк и j столбцов, где i — число строк, j — число столбцов;
Z — диагональная матрица сопротивлений, число строк и столбцов равно числу ветвей;
Сt — транспонированная С-матрица. В транспонированной матрице строки и столбцы меняются местами;
I — матрица КТ (состоит из одного столбца);
J — матрица-столбец — источники тока;
E — матрица-столбец, содержащая ЭДС-источники с тем или иным знаком.

Окончательное уравнение для расчётов в матричном представлении имеет следующий вид:

С * Z * Сt * I = С * (E + Z * J)

Пример использования МКТ

На Рис.2 изображена двухконтурная схема с четырьмя резисторами и двумя источниками напряжения. Применим МКТ для определения реальных токов J1, J2, J3. Пускай R1 = R2 = 4 Ом, R3 = 1 Ом, R4 = 3 Ом, Е1 = 24В, Е2 = 12 В.

Следуя МКТ, сформируем два уравнения. Пускай контурные токи I11 и I22 двигаются по часовой стрелке, тогда:

I11 * (R1 + R2) - I22 * R2 = Е1 - Е2
- I11 * R2 + I22 * (R2 + R3 + R4) = Е2

Подставив численные значения резисторов и источников напряжений, получим:

I11 * 8 - I22 * 4 = 12
- I11 * 4 + I22 * 8 = 8

Далее получаем: I11 = I22 = 3 А. На следующем этапе перейдём от КТ к настоящим токам. В первой ветви течет единственный КТ — I11, совпадающий с J1 по направлению, откуда следует: J1 = I11 = 3 А. Во второй ветке настоящий ток образуется из I11 и I22.

Поскольку I22 совпадает по направлению с J2, а I11 противоположен J2, то: J2 = I22 - I11 = 3 A - 3 A = 0 А. Через третью ветвь проходит единственный КТ I22, противоположный реальному, значит, J3 = - I22 = - 3 А. Итак: J1 = 3 А, J2 = 0 А, J3 = - 3 А.

Заключение

МКТ позволяет существенно упростить нахождение точных значений токов путем уменьшения числа уравнений. Следует заметить, что данная методика не работает, если в электрической схеме присутствуют пересекающиеся ветви.

В каждой электрической цепи имеются так называемые Р – ребра (они же ветви, звенья, участки) и У – узлы. Для ее описания существует система уравнений, в которых используются два правила Кирхгофа. В них, в качестве независимых переменных, выступают токи ребер. Поэтому количество независимых переменных будет равно количеству уравнений, что дает возможность нормального разрешения данной системы. На практике используются методы, направленные на сокращение числа уравнений. Среди них очень часто используется метод контурных токов, позволяющий выполнять расчеты и получать точные результаты.

Суть метода контурных токов

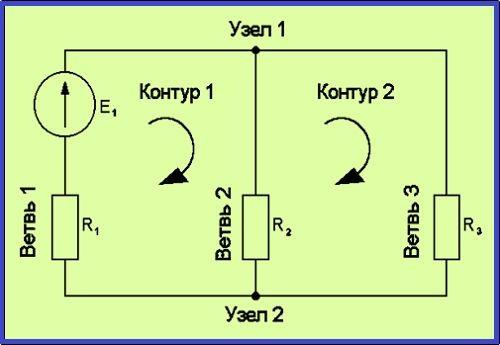
Основные принципы данного метода основываются на том факте, что протекающие в ребрах цепи токи, не все считаются независимыми. Присутствующие в системе У-1 уравнения для узлов, четко показывают зависимость от них У-1 токов. При выделении в электрической цепи независимого тока Р-У+1, вся система может быть сокращена до уравнений Р-У+1. Таким образом, метод контурных токов представляет собой очень простое и удобное выделение в цепи независимых токов Р-У+1.

Использование данного способа расчетов допускает, что в каждом независимом контуре Р-У+1 осуществляется циркуляция определенного виртуального контурного тока. Если какое-либо ребро относится лишь к одному конкретному контуру, то значение протекающего в нем реального тока будет равно контурному. В том случае, когда ребро входит в состав сразу нескольких контуров, ток, протекающий в нем, будет представлять собой сумму, включающую в себя соответствующие контурные токи. В этом случае обязательно учитывается направление обхода контуров. Независимыми контурами перекрывается практически вся схема, поэтому ток, протекающий в каком угодно ребре может быть выражен путем контурных токов, составляющих полную систему всех токов.

Для того чтобы построить систему независимых контуров, используется простой и наглядный метод создания планарных графов. На данной схеме ветви и узлы цепи размещаются на плоскости таким образом, что взаимное пересечение ребер полностью исключается. С помощью этого метода плоскость разбивается на области, ограниченные замкнутыми цепочками ребер. Именно они и составляют систему независимых контуров. Данный метод более всего подходит для ручных расчетов схем. Однако его применение может стать затруднительным или вовсе невозможным, если рассматриваемая схема не укладывается в рамки планарного графа.

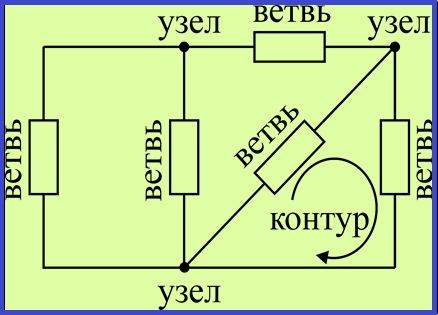
Другим способом расчетов служит метод выделения максимального дерева. Само дерево представлено в виде подмножества звеньев электрической цепи и является односвязным графом, в котором отсутствуют замкнутые контуры. Для того чтобы оно появилось, из цепи постепенно исключаются некоторые звенья. Дерево становится максимальным, когда к нему добавляется любое исключенное звено, в результате чего образуется контур.

Применение метода выделения максимального дерева представляет собой последовательное исключение из цепи заранее установленных звеньев в соответствии с определенными правилами. Каждый шаг в цепи предполагает произвольное исключение одного звена. Если такое исключение нарушает односвязность графа, разбивая его на две отдельные части, в этом случае звено может возвратиться обратно в цепь. Если граф остается односвязным, то и звено остается исключенным. В конечном итоге, количество звеньев, исключенных из цепи, оказывается равным количеству независимых контуров, расположенных в схеме. Получение каждого нового независимого контура связано с присоединением к электрической цепи конкретного исключенного звена.

Применение метода контурных токов для расчета цепи

В соответствии с этой методикой, неизвестными величинами являются расчетные или контурные токи, предположительно протекающие во всех независимых контурах. В связи с этим, все неизвестные токи и уравнения в системе, равны количеству независимых контуров электрической цепи.

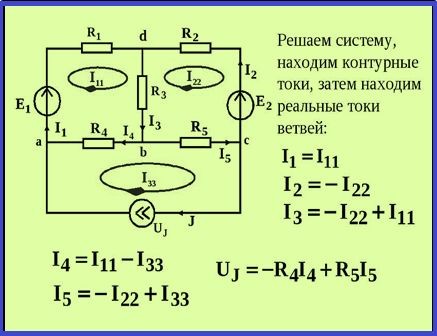
Токи ветвей в соответствии с данным методом рассчитываются следующим образом:

В первую очередь вычерчивается схема цепи с обозначением всех ее элементов.
Далее определяется расположение всех независимых контуров.
Направления протекания контурных токов задаются произвольно по часовой или против часовой стрелки в каждом независимом контуре. Они обозначаются с использованием цифровых или комбинированных символов.
В соответствии со вторым законом Кирхгофа, затрагивающего контурные токи, составляются уравнения для всех независимых контуров. В записанном равенстве направления обхода контура и контурного тока этого же контура совпадают. Необходимо учитывать и то обстоятельство, что в ветвях, расположенных рядом, протекают собственные контурные токи. Падение напряжения потребителей берется отдельно от каждого тока.
Следующим этапом является решение полученной системы любым удобным методом, и окончательное определение контурных токов.
Нужно задать направление реальных токов во всех ветвях и обозначить их отдельной маркировкой, чтобы не перепутать с контурными.
Далее нужно от контурных токов перейти к реальным, исходя из того, что значение реального тока конкретной ветви составляет алгебраическую сумму контурных токов, протекающих по этой ветви.

Если направление контурного тока совпадает с направлением реального тока, то при выполнении алгебраического суммирования математический знак не меняется. В противном случае значение контурного тока нужно умножить на -1.

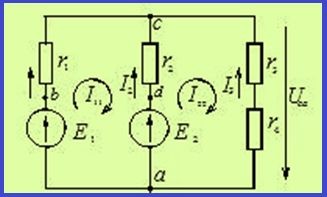
Метод контурных токов очень часто применяется для расчетов сложных цепей. В качестве примера для приведенной схемы нужно задать следующие параметры: Е1 = 24В, Е2 = 12В, r1 = r2 = 4 Ом, r3 = 1 Ом, r4 = 3 Ом.

Для решения этой сложной задачи составляются два уравнения, соответствующие двум независимым контурам. Направление контурных токов будет по часовой стрелке и обозначается I₁₁ и I₂₂. На основании второго закона Кирхгофа составляются следующие уравнения:

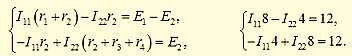
После решения системы получаются контурные токи со значением I₁₁ = I₂₂ = 3 А. Далее произвольно обозначается направление реальных токов, как I1, I2, I3. Все они имеют одинаковое направление – вверх по вертикали. После этого выполняется переход от контурных к реальным. В первой ветви имеется течение только одного контурного тока т I₁₁. Его направление совпадает с реальным током, поэтому I1 + I11 = 3 А.

Формирование реального тока во второй ветке осуществляется за счет двух контурных токов I₁₁ и I₂₂. Направление тока I₂₂ совпадает с реальным, а направление I₁₁ будет строго противоположно реальному. Таким образом, I2 = I₂₂ – I₁₁ = 3 – 3 = 0 А. В третьей ветке I3 наблюдается течение лишь контурного тока I₂₂. Его направление будет противоположным направлению реального тока, поэтому в данном случае расчеты выглядят следующим образом: I3 = -I22 = -3А.

Основным положительным качеством метода контурных токов по сравнению с вычислениями по законам Кирхгофа, является значительно меньшее количество уравнений, используемых для вычислений. Тем не менее, здесь присутствуют определенные сложности. Например, реальные токи ветвей не всегда удается определить быстро и с высокой точностью.

Все расчеты электрических схем базируются на простых формулах. Сложность и громоздкость вычислений зависят от сложности схем. Для упрощения расчетов без ущерба качеству разработано несколько методик, позволяющих сократить число вычислений до разумных пределов.

Основные принципы

Любая электротехническая цепь состоит из участков (ветвей), образующих узлы и контуры. Для определения значений тока через любой элемент используют два закона Кирхгофа. Прямое составление уравнений дает систему с их максимальным количеством, равным количеству ветвей. В результате, если множество узлов цепи равно У, а число ветвей Р, то уравнения распределяются следующим образом:

Для узлов У-1 по закону Кирхгофа для токов;
Для ветвей Р-У+1 по закону Кирхгофа для напряжений.

Данное количество избыточно и приводит к образованию громоздкой системы уравнений большой размерности.

Для упрощения расчетов разработаны методики, которые позволяют сократить количество уравнений до приемлемых значений без снижения точности результатов. Наиболее простым является метод контурных токов.

Определение и суть метода контурных токов

По данному методу в исследуемой цепи выделяются независимые плоские замкнутые контуры, включающие все, без исключения, элементы. Предполагается, что в каждом контуре может протекать некоторый контурный ток. В том случае, если цепь с элементом принадлежит только одному контуру, то ток через входящие в нее элементы равен контурному. Если элемент охватывается несколькими контурами, то он в ней равен алгебраической (с учетом направления) сумме контурных токов.

При составлении уравнений учитываются входящие в схему источники ЭДС и тока.

На практике удобнее преобразовать идеальный источник тока в идеальный источник ЭДС. Преобразование выполняется согласно закона Ома:

U=I∙r, где r – внутреннее сопротивление источника тока (напряжения).

Методика расчета используется как в цепях постоянного, так и переменного напряжения. При расчетах цепей переменного напряжения с реактивными элементами используются комплексные величины, затем вычисляются мгновенные и амплитудные величины токов и напряжений и углы сдвига фаз между ними.

Построение системы контуров

Основная сложность заключается в правильном выделении контуров. Количество контурных токов будет равняться числу выбранных контуров.

Важно! Каждый элемент схемы должен входить хотя бы в один контур.

Распространены две методики выбора контуров.

Использование планарных графов

Метод планарных графов применяется при ручном расчете, поскольку он наиболее прост и нагляден. Для построения плоского графа схему рисуют таким образом, чтобы не было взаимного пересечения ветвей. Получается, что схему можно разбить на несколько ограниченных участков, которые образуют контуры.

Рассматриваемая методика неприменима без дополнительных преобразований, если невозможно выразить схему в виде планарного графа.

Метод выделения максимального дерева

Метод выделения максимального дерева более абстрактный и используется при автоматизированных расчетах и наличия специализированных программ. Суть метода заключается в исключении из цепи некоторых ветвей в соответствии со строгими правилами, которые таковы:

Построение системы уравнений

Построение системы уравнений по рассматриваемой методике выполняется по следующим правилам:

После выполнения арифметических действий (раскрытие скобок, приведение подобных слагаемых) получается система уравнений, в которых неизвестными величинами являются виртуальные контурные токи.

Решая систему уравнений, получают значения контурных, а затем искомых величин.

Оптимизированная процедура составления системы

По упрощенной методике поступают следующим образом:

В уравнениях в левой части записывают произведение суммы всех входящих в контур сопротивлений на контурный ток;
От полученного выражения вычитаются умноженные на сумму сопротивлений общей ветви соседние контурные токи;
Справа записывается сумма источников ЭДС контура.

Формальный подход

Формальный подход предполагает матричную форму записи системы уравнений. Для расчетов исходные данные записывают в матричной форме. Используются такие матрицы:

C – в которой i строк, соответствующих количеству контуров, и j столбцов по количеству ветвей;
Z – диагональная матрица сопротивлений, количество строк и столбцов которой соответствуют числу веток;
Ct – транспонированная матрица С;
I – матрица контурных величин;
J – матрица источников тока;
Е – матрица ЭДС.

При составлении матрицы С каждый элемент Сij:

0, если ветвь j не входит в контур;
-1, если ветвь входит в контур, направление тока противоположно контурному;
1 – то же самое, но направление тока совпадает с контурным.

В матрице Z диагональные элементы равняются сопротивлению участков, остальные приравниваются нулю.

Итоговая формула для расчетов имеет вид:

Такая форма записи решения в матричной форме показывает, каким образом выполняются действия над составленными матрицами.

Пример системы уравнений

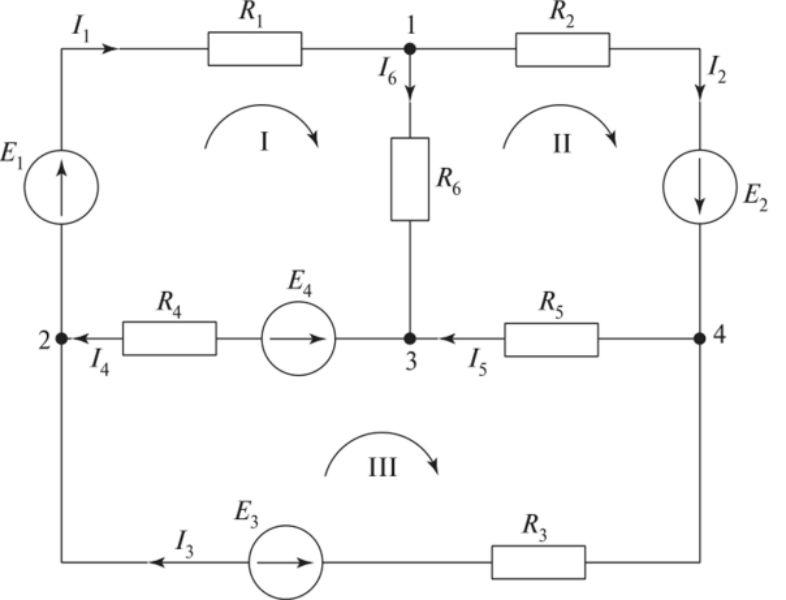
Ниже рассмотрен пример расчета конкретной схемы без учета номиналов элементов.

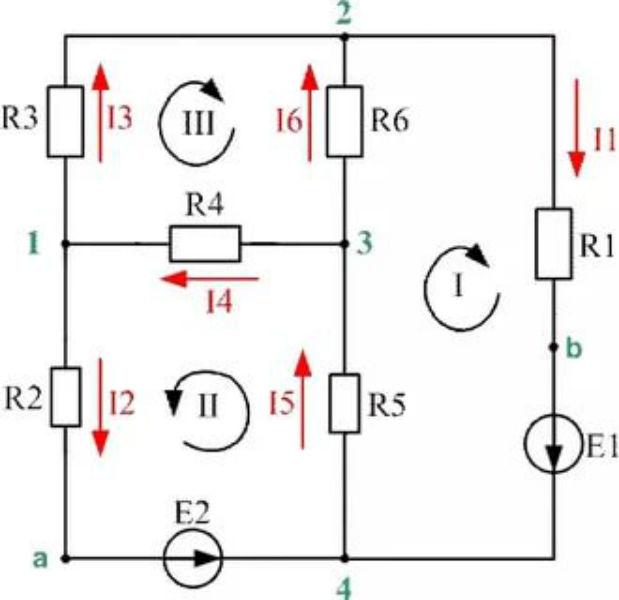
В заданной цепи выделяют три контура. Как выразить токи в ветвях через контурные:

i1=I1;
i2=I2;
i3=I3;
i4=I2+I3;
i5=I1+I2;
i6=I1-I3.

Как составить систему уравнений:

i1R1+i5R5+i6R6=E1;
i2R2+i4R4+i5R5=E2;
i3R3+i4R4-i6R6=0

Как подставить контурные значения:

I1R1+( I1+I2)R5+( I1-I3)R6=E1;
I2R2+( I2+I3)R4+( I1+I2)R5=E2;
I3R3+( I2+I3)R4-( I1-I3)R6=0

После преобразования получается необходимая система уравнений:

(R1+R5+R6)I1+R5I2+R6I3=E1;
R5I1+(R2+R4+R5)I2+R4I3=E2;
-R6I1+R4I2+(R3+R4+R6)I3=0.

Система из трех уравнений легко решается после подстановки известных параметров. Из полученных значений контурных токов затем можно найти искомые величины.

Данный пример решения задач по методу контурных токов показывает, что любую достаточно сложную схему можно существенно упростить для решения, руководствуясь указаниями.

Важно! Метод неприменим, если нет возможности преобразовать цепь без взаимного пересечения ветвей.

Точно такие же результаты получаются при использовании метода узловых потенциалов. В основе расчетов – поиск потенциала каждого узла (так называемый узловой потенциал). Существуют программы, позволяющие произвести онлайн расчет параметров по рассмотренным методам.

Видео

Читайте также: