Каково основное содержание матрицы кратчайших расстояний

Обновлено: 05.07.2024

В математике , информатике и особенно теории графов , А матрица расстояний является квадратная матрица (двумерный массив) , содержащий расстояния , взятые попарно, между элементами набора. В зависимости от задействованного приложения расстояние , используемое для определения этой матрицы, может быть или не быть метрикой . Если есть N элементов, эта матрица будет иметь размер N × N . В теоретико-графических приложениях элементы чаще называют точками, узлами или вершинами.

СОДЕРЖАНИЕ

Неметрические матрицы расстояний

В общем случае матрица расстояний - это взвешенная матрица смежности некоторого графа. В сети , ориентированном графе с весами, присвоенными дугам, расстояние между двумя узлами сети можно определить как минимум сумм весов на кратчайших путях, соединяющих два узла. Эта функция расстояния, хотя и хорошо определена, не является метрикой. Не требуется никаких ограничений на веса, кроме необходимости иметь возможность комбинировать и сравнивать их, поэтому в некоторых приложениях используются отрицательные веса. Поскольку пути являются направленными, симметрия не может быть гарантирована, и если существуют циклы, матрица расстояний не может быть пустой.

Алгебраическая формулировка сказанного выше может быть получена с помощью алгебры мин-плюс . Умножение матриц в этой системе определяется следующим образом: для двух матриц и их произведение расстояний определяется как матрица, такая что . Обратите внимание, что для недиагональных элементов, которые не связаны напрямую, необходимо установить бесконечность или подходящее большое значение для правильной работы операций min-plus. Ноль в этих местах будет неправильно интерпретирован как грань без расстояния, стоимости и т. Д. п × п А знак равно ( а я j ) )> B знак равно ( б я j ) )> C знак равно ( c я j ) знак равно А ⋆ B ) = A \ звезда B> п × п c я j знак равно мин k знак равно 1 п < а я k + б k j > = \ min _ ^ \ + b_ \>>

Если - матрица, содержащая веса ребер графа , то (с использованием этого произведения расстояний) дает расстояния между вершинами, используя пути длины на большинстве ребер, и является матрицей расстояний графа. W п × п W k > k W п >

Произвольный граф G на n вершинах можно смоделировать как взвешенный полный граф на n вершинах, присвоив вес, равный единице, каждому ребру полного графа, который соответствует ребру G, и нулю всем остальным ребрам. W для этого полного графа является матрица смежности из G . Матрица расстояний G может быть вычислена из W, как указано выше, однако W n, вычисленное обычным умножением матриц, кодирует только количество путей между любыми двумя вершинами длины ровно n .

Матрицы метрических расстояний

Ценность формализма матрицы расстояний во многих приложениях заключается в том, как матрица расстояний может явно кодировать аксиомы метрики и в том, как она поддается использованию методов линейной алгебры. То есть, если M = ( x _ij ) с 1 ≤ i , j ≤ N - матрица расстояний для метрического расстояния, то

1. все элементы на главной диагонали равны нулю (то есть матрица является пустой матрицей ), т.е. x_ii = 0 для всех 1 ≤ i ≤ N ,
2. все недиагональные элементы положительны ( x_ij > 0, если i ≠ j ) (то есть неотрицательная матрица ),
3. матрица является симметричной матрицей ( x_ij = x_ji ), и
4. для любых i и j , x_ij ≤ x_ik + x_kj для всех k (неравенство треугольника). Это можно сформулировать в терминах умножения тропических матриц

Когда матрица расстояний удовлетворяет первым трем аксиомам (что делает ее полуметрической), ее иногда называют матрицей предварительных расстояний. Матрица предварительных расстояний, которая может быть встроена в евклидово пространство, называется матрицей евклидовых расстояний .

Другой распространенный пример метрической матрицы расстояний возникает в теории кодирования, когда в блочном коде элементы представляют собой строки фиксированной длины по алфавиту, а расстояние между ними задается метрикой расстояния Хэмминга . Наименьший ненулевой элемент в матрице расстояний измеряет способность кода исправлять и обнаруживать ошибки.

Приложения

Иерархическая кластеризация

Матрица расстояний необходима для иерархической кластеризации .

Филогенетический анализ

Матрицы расстояний используются в филогенетическом анализе .

Другое использование

В биоинформатике матрицы расстояний используются для представления структур белков независимым от координат образом, а также попарных расстояний между двумя последовательностями в пространстве последовательностей. Они используются для структурного и последовательного выравнивания, а также для определения структур белков с помощью ЯМР или рентгеновской кристаллографии .

Иногда удобнее представить данные в виде матрицы сходства .

Он используется для определения корреляции расстояний .

Примеры

Например, предположим, что эти данные должны быть проанализированы, где евклидово расстояние пикселя является метрикой расстояния .

Матрица расстояний будет следующей:

а	б	c	d	е	ж
а	0	184	222	177	216	231
б	184	0	45	123	128	200
c	222	45	0	129	121	203
d	177	123	129	0	46	83
е	216	128	121	46	0	83
ж	231	200	203	83	83	0

Затем эти данные можно просмотреть в графической форме в виде тепловой карты . На этом изображении черный цвет обозначает расстояние 0, а белый - максимальное расстояние.

В математика, Информатика и особенно теория графов, а матрица расстояний это квадратная матрица (двумерный массив), содержащий расстояния, взятые попарно, между элементами множества. [1] В зависимости от используемого приложения расстояние используется для определения этой матрицы, может быть или не быть метрика. Если есть N элементов, эта матрица будет иметь размер N×N . В теоретико-графических приложениях элементы чаще называют точками, узлами или вершинами.

Содержание

Неметрические матрицы расстояний

В общем случае матрица расстояний представляет собой взвешенную матрица смежности некоторого графа. В сеть, а ориентированный граф с весами, присвоенными дугам, расстояние между двумя узлами сети можно определить как минимум сумм весов на кратчайших путях, соединяющих два узла. [2] Эта функция расстояния, хотя и хорошо определена, не является метрикой. Не требуется никаких ограничений на веса, кроме необходимости иметь возможность комбинировать и сравнивать их, поэтому в некоторых приложениях используются отрицательные веса. Поскольку пути являются направленными, симметрия не может быть гарантирована, и если существуют циклы, матрица расстояний не может быть пустой.

Произвольный граф грамм на п вершины можно моделировать как взвешенный полный граф на п вершин, присвоив вес один каждому ребру полного графа, который соответствует ребру грамм и ноль ко всем остальным краям. W для этого полного графа матрица смежности из грамм . Матрица расстояний грамм можно вычислить из W как указано выше, однако, W п рассчитывается обычным матричное умножение кодирует только количество путей между любыми двумя вершинами длиной не более п .

Матрицы метрических расстояний

Ценность формализма матрицы расстояний во многих приложениях заключается в том, как матрица расстояний может явно кодировать метрические аксиомы и как она поддается использованию методов линейной алгебры. То есть, если M = (Икс_ij) с 1 ≤ я, j ≤ N матрица расстояний для метрического расстояния, тогда

1. все элементы на главной диагонали равны нулю (то есть матрица является полая матрица), т.е. Икс_ii = 0 для всех 1 ≤ я ≤ N ,
2. все недиагональные элементы положительны ( Икс_ij > 0 если я ≠ j ), (это неотрицательная матрица),
3. матрица - это симметричная матрица ( Икс_ij = Икс_джи ), и
4. для любого я и j , Икс_ij ≤ Икс_ik + Икс_кДж для всех k (неравенство треугольника). Это можно выразить в терминах умножение тропических матриц

Когда матрица расстояний удовлетворяет первым трем аксиомам (что делает ее полуметрической), ее иногда называют матрицей предварительных расстояний. Матрица предварительных расстояний, которую можно вложить в евклидово пространство, называется Матрица евклидовых расстояний.

Другой распространенный пример метрической матрицы расстояний возникает в теория кодирования когда в код блока элементы представляют собой строки фиксированной длины по алфавиту, а расстояние между ними задается Расстояние Хэмминга метрика. Наименьший ненулевой элемент в матрице расстояний измеряет способность кода исправлять и обнаруживать ошибки.

Приложения

Иерархическая кластеризация

Матрица расстояний необходима для иерархическая кластеризация.

Филогенетический анализ

Матрицы расстояний используются в филогенетический анализ.

Другое использование

В биоинформатика, матрицы расстояний используются для представления белок структуры независимо от координат, а также попарные расстояния между двумя последовательностями в пространстве последовательностей. Они используются в структурный и последовательный выравнивания, а также для определения белковых структур из ЯМР или же Рентгеновская кристаллография.

Иногда удобнее выражать данные как матрица сходства.

Он используется для определения корреляция расстояний.

Примеры

Например, предположим, что эти данные должны быть проанализированы, где пиксель Евклидово расстояние это метрика расстояния.

Матрица расстояний будет следующей:

а	б	c	d	е	ж
а	0	184	222	177	216	231
б	184	0	45	123	128	200
c	222	45	0	129	121	203
d	177	123	129	0	46	83
е	216	128	121	46	0	83
ж	231	200	203	83	83	0

Затем эти данные можно просмотреть в графической форме как Тепловая карта. На этом изображении черный цвет обозначает расстояние 0, а белый - максимальное расстояние.

Сгруппировав пункты по маршрутам, переходим ко вто­рому этапу.

Этап 2. Определяем рациональный порядок объезда пун­ктов каждого маршрута. Для этого строим таблицу-матри­цу, в которой по диагонали размещаем пункты, включае­мые в маршрут, и начальный пункт А, в соответствующих клетках (на пересечении пунктов) — кратчайшие расстоя­ния между ними (табл. 6.6).

Кратчайшее расстояние между А и Г — 3,0 км. Пишем 3,0 на пересечении строк А и Г, под А. Кратчайшее рассто­яние между А и Е: А-Г + Г-Е = 7,0. Пишем 7,0 на пересече­нии строк А и Е, под А. Для маршрута А-Л может быть пять вариантов движения:

8,0 км — наименьшее расстояние между А и Л, его и пишем на пересечении строк А и Л, под А. Таким образом заполняется вся матрица.

Начальный маршрут строим для трех пунктов матри­цы, из которых один является пунктом отправления, а два

Используя этот метод и формулу приращения, опреде­ляем, между какими пунктами расположить пункты Е и Л. Начнем с пункта Л, так как размер суммы этого пункта больше.

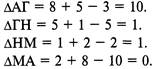
Таким образом, пункт Л включается между пунктами М и А, и из маршрута А-Г-Н-М-А мы получаем маршрут А-Г-Н-М-Л-А.

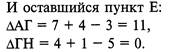
Минимальным значением является ∆ГН == 0, значит, пункт Е включается между пунктами Г и Н. В результате мы имеем оптимальный маршрут развоза продукцииА-Г-Е-Н-М-Л-А =3+4+1+2+2+10 =22 км.

Таким же методом определим кратчайший путь объез­да пунктов по маршруту 2. В результате расчетов получим маршрутА-В-К-Д-Б-А =1+4+2+2+3= 12 км. Порядок движения по полученным оптимальным маршрутам пока­зан на рис. 6.5.

Принцип алгоритма Дейкстры по кратчайшему пути и реализация Matlab

Базовые знания теории графов более не разработаны.
Существует два основных алгоритма кратчайшего пути

Алгоритм Дейкстры изучаетКратчайший путь от начальной точки до каждого другого узла
Алгоритм ФлойдаКратчайший путь между любыми двумя узлами

Возьмите следующую картину в качестве примера, сначала представьте принцип Диджстра

Красная буква - это номер каждого узла, а синее слово - это расстояние между каждым узлом.

Сначала определите несколько переменных

Количество узлов n;
Двумерная матрица M (nxn), матрица расстояний, расстояние между соединенными узлами - это расстояние, расстояние между неподключенными узлами равно положительной бесконечности, а расстояние от себя равно 0;
Одномерная матрица pb (1xn), если i-я точка нашла кратчайший путь, то fp (i) = 1, в противном случае она равна 0, для начального узла fp = 1;
Матрица расстояний d (1xn), если i-я точка нашла кратчайший путь, то d (i) = кратчайшее расстояние, в противном случае 0, начальный узел d = 0;
Предыдущий путь матрицы узлов (1xn), если кратчайший путь найден в i-й точке, путь хранит предыдущий узел этого кратчайшего пути. Проследив до каждой точки, вы можете Найдите кратчайший путь.

Запишите следующую матрицу расстояний в соответствии с расстоянием

Определите, что начальная точка v1, тогда pb (1) = 1;

На рисунке в узле мы отмечаем точку, в которой был найден кратчайший путь, в качестве его кратчайшего расстояния (можно понять, что точка v1 нашла кратчайший путь, а расстояние равно 0), а остальные точки, которые не найдены, перечислены как положительная бесконечность (т.е. Значит не подключен).

В точке, связанной с v1, то есть в первой строке матрицы m найдите минимальное значение, столбец, в котором находится минимальное значение, является узлом самого короткого определенного пути, поскольку v2 является самым коротким, pb ( 2) = 1, d (2) = 1, предыдущим узлом v2, который нашел кратчайший путь, является v1, path (2) = 1;

Далее в

• Расстояние узла, подключенного к v1, и кратчайшее расстояние не найдено
• Соединен с v2, и расстояние от ближайшего узла не найдено + кратчайшее расстояние от v2

Найдите самое короткое расстояние среди двух вышеупомянутых, самое короткое - v6, pb (6) = 1; d (6) = 2; путь (6) = 1;

Повторите вышеуказанные шаги в

• Расстояние узла, подключенного к v1, и кратчайшее расстояние не найдено
• Соединен с v2, и расстояние от ближайшего узла не найдено + кратчайшее расстояние от v2
• Соединен с v6, и расстояние от кратчайшего узла расстояния не найдено + кратчайшее расстояние от v2
  Найдите кратчайший путь из вышеперечисленных трех, кратчайшим является v3, pb (3) = 1; d (3) = 3); path (3) = 6;
  
  Мы можем обнаружить, что самый короткий путь
  Для точки, где был найден кратчайший путь (включая начальный узел), среди подключенных к нему узлов кратчайший путь не найден, расстояние между расстоянием и окружностью Кратчайший путь, найденный в узле), добавляется для получения минимального значения.
  Если существует несколько одинаковых кратчайших расстояний, выберите одно из них.
  Последний кратчайший путь - это расстояние, как показано ниже
  

Читайте также:

  
• Сценарий новогоднего вечера в школе для старшеклассников
  
• Кратко сформулированные основные положения научного произведения
  
• Технические навыки детей и действия воспитателя по их развитию в доу
  
• Выборочное изложение на тему кладовая солнца
  
• 28 школа брест психолог