Длина тел в разных системах отсчета лоренц кратко
Обновлено: 01.07.2024
Ранее мы уже изучили формулы, называемые классическими преобразованиями Галилея, однако они несовместимы с постулатами специальной теории относительности (СТО). Поэтому в данном случае нам нужно использовать другие положения. Благодаря новым преобразованиям мы сможем установить, какая связь существует между некоторым моментом события t , наблюдаемого в системе отсчета K в точке с координатами ( x , y , z ) и показателями того же события, которое наблюдается в системе отсчета K ' .
Преобразования Лоренца представляют собой кинематические формулы, с помощью которых происходит преобразование координат и времени в специальной теории относительности.
Они были впервые сформулированы еще в 1904 году в качестве преобразований, относительно которых были инвариантны уравнения электродинамики.
Обозначим основные системы K и K ' , скорость их движения – υ , а ось, вдоль которой они движутся – x . В таком случае преобразования Лоренца примут следующий вид:
K ' → K x = x ' + υ t ' 1 - β 2 , y = y ' , z = z ' , t = t ' + υ x ' / c 2 1 - β 2 . K → K ' x ' = x - υ t 1 - β 2 , y ' = y , z ' = z , t ' = t - υ x / c 2 1 - β 2 .
Используя эти формулы, мы можем вывести из них множество следствий. Так, именно из системы преобразований Лоренца следует лоренцево сокращение длины и релятивистский эффект замедления времени.
Возьмем случай, когда в системе K ' происходит некий процесс, длительность которого составляет τ 0 = t ' 2 – t ' 1 (по собственному времени). Здесь t ' 1 и t ' 2 – это время на часах в начале данного процесса и в его конце. Чтобы вычислить его общую продолжительность в точке x , необходимо взять для расчета следующую формулу:
τ = t 2 - t 1 = t ' 2 + υ x ' / c 2 1 - β 2 - t ' 1 + υ x ' / c 2 1 - β 2 = t ' 2 - t ' 1 1 - β 2 = τ 0 1 - β 2 .
Формула релятивистского сокращения длины выводится из преобразований Лоренца точно таким же образом.
Принцип относительности одновременности
Еще одно важное следствие, которое необходимо знать, – это положение о том, что любая одновременность относительна.
Например, если в системе отсчета K ' взять две разные точки, в которых некий процесс будет протекать одновременно (с позиции стороннего наблюдателя), то в системе наблюдатель будет иметь следующее:
x 1 = x ' 1 + υ t ' 1 - β 2 , x 2 = x ' 2 + υ t ' 1 - β 2 ⇒ x 1 ≠ x 2 , t 1 = t ' + υ x ' 1 / c 2 1 - β 2 , t 2 = t ' + υ x ' 2 / c 2 1 - β 2 ⇒ t 1 ≠ t 2 .
Из этого вытекает пространственная разобщенность данных событий в системе K , следовательно, они не могут считаться одновременными. Нельзя сразу сказать, какое событие будет происходить первым, а какое вторым, поскольку это определяется особенностями системы отсчета – знак разности будет определен знаком выражения υ ( x ' 2 – x ' 1 ) .
Если между событиями имеется причинно-следственная связь, то данный вывод специальной теории относительности для них использовать нельзя. Однако мы можем показать, что при этом не нарушается принцип причинности, и события следуют в нужном порядке в любой инерциальной системе отсчета.
Разберем пример, показывающий, что одновременность разобщенных в пространстве событий является относительной.
Возьмем систему отсчета K ' и расположим в ней длинный жесткий стержень. Его положение будет неподвижным и ориентированным вдоль оси абсцисс. Установим на оба его конца часы, синхронизированные между собой, а в центр поместим импульсную лампу. Также у нас будет система K ' , совершающая движение вдоль оси x в системе K .
В определенный момент времени лампа включится и пошлет световые сигналы в направлении обоих концов жесткого стержня. Поскольку она находится точно в центре, эти сигналы должны дойти до концов в одно и то же время t , которое должно быть зафиксировано расположенными на них часами. Однако концы стержня движутся относительно системы K так, что один конец стремится навстречу световому сигналу, а другой конец свету приходится догонять. Скорость света, распространяющегося в оба направления, одинакова, но сторонний наблюдатель скажет, что до левого конца свет дошел быстрее, чем до правого.
Рисунок 4 . 4 . 1 . Иллюстрация принципа относительности одновременности: достижение световым импульсом концов стержня в системе K ' в одно и то же время и в системе K в разное.
Инвариантные величины в СТО
Данные преобразования нужны нам для выражения относительного характера временных промежутков и промежутков расстояний. Вместе с тем в специальной теории относительности помимо утверждения относительного характера времени и пространства очень важно установить инвариантные физические величины, не изменяющиеся при смене системы отсчета. Подобной величиной является скорость света в вакууме, чей характер в рамках СТО становится абсолютным. Также важна такая величина, как интервал между событиями, поскольку именно она выражает абсолютность пространственно-временной связи.
Для вычисления пространственно-временного интервала необходимо использовать следующую формулу:
s 12 = c 2 t 12 2 - l 12 2 .
В ней с помощью параметра l 12 выражено расстояние между точками одной системы, где совершаются события, а t 12 – это временной промежуток между теми же самыми событиями. Если местом одного из событий является начало координат, т.е. x 1 = y 1 = z 1 = 0 и ( t 1 = 0 ) , а второе происходит в точке с координатами x , y , z в некоторое время t , то формула вычисления пространственно-временного интервала между ними записывается так:
s = c 2 t 2 - x 2 - y 2 - z 2 .
Преобразования Лоренца дают нам возможность доказать неизменность пространственно-временного интервала между событиями при смене инерциальной системы.
Если величина интервала не зависит от того, какая система отсчета используется, т.е. является объективной при любых относительных расстояниях и временных промежутках, то такой интервал называется инвариантным.
Допустим, что у нас есть событие (вспышка света), которое произошло в точке начала координат в некоторой системе во время, равное 0 , а потом свет переместился в другую точку с координатами x , y , z во время t . Тогда мы можем записать следующее:
x 2 + y 2 + z 2 = c 2 t 2 .
У нас получилось, что интервал этой пары событий будет равен нулю. Если мы поменяем систему координат и возьмем другое время для второго события, то результаты окажутся точно такими же, поскольку:
x 2 + y 2 + z 2 = c 2 t 2
Иначе говоря, любые два события, которые связывает между собой световой сигнал, будут иметь нулевой пространственно-временной интервал.
Также формулы Лоренца для времени и координат можно использовать для выведения релятивистского закона сложения скоростей.
Например, у нас есть частица, которая находится в системе отсчета K ' и движется в ней вдоль оси абсцисс со скоростью u ' x = d x ' d t ' . Параметры скорости u ' x и u ' равны 0 . В системе K , соответственно, скорость будет равна u x = d x d t .
Применим к одной из формул преобразования Лоренца операцию дифференцирования и получим следующее:
u x = u ' x + υ 1 + υ c 2 u ' x , u y = 0 , u z = 0 .
Данные отношения являются выражением релятивистского закона сложения скоростей. Он применим в случае движения частицы параллельно относительной скорости υ → в системах отсчета K и K ' .
Если υ ≪ c , то релятивистские отношения могут быть преобразованы в формулы классической механики:
u x = u ' x + υ , u y = 0 , u z = 0 .
Если мы имеем дело со световым импульсом, распространяющимся в системе K ' вдоль оси x ' со скоростью u ' x = c , то в этом случае применима следующая формула:
u x = c + υ 1 + υ / c = c , u y = 0 , u z = 0 .
Иначе говоря, скорость распространения светового импульса в системе K вдоль оси x также будет равна c , что соответствует постулату об инвариантности скорости света.
которому все законы механики одинаковы во всех инерциальных системах отсчета.
Математически принцип относительности в классической механике выражается с помощью преобразования Галилея — закона сложения скоростей при переходах от одной инерциальной системы отсчета к другой.
Согласно этому закону скорость тела в неподвижной системе отсчета представляет собой сумму скорости тела по отношению к движущейся системе отсчета и скорости самой системы отсчета по отношению к неподвижной. Для всех наблюдаемых движений в природе, скорости которых малы по сравнению со скоростью света, этот закон выполняется с точностью, которая не давала оснований сомневаться в его справедливости вплоть до конца 19-го столетия.
Измерения скорости света, проведенные с большой точностью, показали, что закон сложения скоростей Галилея не выполняется для световых лучей. Скорость света, измеренная в движущейся системе координат, оказалась в точности такой же, как и для неподвижной системы отсчета.
Таким образом, был установлен экспериментальный факт независимости скорости света от скорости движения источников либо приемников света. Другими словами, было установлено, что скорость света является абсолютной постоянной величиной, равной скорости света в пустоте – .
Этот факт невозможно совместить с принципом относительности Галилея.
Возникшее противоречие в классической механике привело А. Эйнштейна к необходимости допустить, что классическая механика справедлива лишь для скоростей малых по сравнению со скоростью света. При скоростях движения, сравнимых со скоростью света, справедлива созданная А. Эйнштейном механика специальной теории относительности, или, как ее называют, релятивистская механика.
Принцип относительности Эйнштейна состоит в том, что не только законы механики, но и вообще все физические законы должны не зависеть от выбранной инерциальной системы отсчета.
Преобразования Лоренца.
Пусть имеются две инерциальные системы отсчета и .
Предполагается, что система движется со скоростью – вдоль оси , в то время как система неподвижна.
Предположим, что происходит какое-то событие.
В системе , оно характеризуется значениями координат и времени x, у, z, t; в системе — значениями координат и времени x', y', z', t'.
Связь между значениями координат в выделенных системах отсчёта даётся с помощью введения, так называемого, Лоренц-фактора – .
ПРИМЕЧАНИЕ.
Лоренц-фактором называется величина
где относительная скорость, .
Итак, для координаты оси (вдоль которой происходит движение!):
Координаты по другим ортогональным осям остаются неизменными,
Формулы (1)÷(3) называются преобразованиями Лоренца.
В пределе при и преобразования Лоренца переходят в преобразования Галилея. Таким образом, различие в течение времени в разных инерциальных системах отсчета обусловлено существованием предельной скорости распространения взаимодействий. При скоростях много меньших скорости света (т. е. при β
1. Относительность понятия одновременности событий, причинно не связанных друг с другом . Количественно, это следствие устанавливается формулами (3).
2.Различный промежуток времени между событиями в разных системах отсчёта. Справедливость утверждения легко установить с помощью формул (3), если промежуток времени определять как разность между начальным и конечым значениями времени.
3.Различная длина тел в разных системах отсчета.
Если длину объекта в направлении движения рассматривать как разность координат его граничных точек, то длина движущегося стержня оказывается меньше той, которой обладает стержень в состоянии покоя. Количественно, этот факт утанавливается зависимостями (1).
4. Релятивистский импульс, релятивистское выражение для энергии.
Формулу, связывающую скорости движения в выделенных системах отсчёта, можно получить дифференцированием зависимостей (1) с учётом соотношений (3).
После выполнения математических операций и необходимых тождественных преобразований получаем, что
Выражение для импульса релятивистской частицы, движущейся со скоростью – , может быть записано в виде (опуская соответствующие математические преобразования с использованием соотношений для координаты и времени – (1) и (3)):
где относительная сворость релятивистской частицы.
В релятивистской механике справедливым остается выражение, описывающее второй закон Ньютона:
Выражения для полной и кинетической энергии релятивистской частицы имеют вид:
гдеE0 = m·c 2 – энергия покоя, то есть, энергия релятивистской частицы
Пример №1.
Ионизованный атом, вылетев из ускорителя заряженных частиц со скоростью , испустил фотон в направлении своего движения. Определить скорость фотона относительно ускорителя.
Решение.

Формула, связывающая скорости движения в различных системах отсчёта, – это формула (3а):
В терминах поставленной задачи можно считать, что скорость фотона равне скорости света в вакууме, то есть . Скорость ионизованного атома на выходе ускорителя – это .
Подставляя числа в формулу для скорости, находим, что
Ответ:скорость фотона относительно ускорителя равна – .
Кинетическая энергия частицы оказалась равной её энергии покоя. Определить скорость частицы.
Решение.
Из формулы (6) получаем, что при
Ответ: в терминах скорости света в вакууме скорость частицы будет равна
Примечание. м/c.
Тест Тулуз-Пьерон (корректурная проба): получение информации о более общих характеристиках работоспособности, таких как.
Длина тел в разных системах отсчета. Сравним длину стержня в инерциальных системах отсчета K и K' (рис.). Предположим, что стержень, расположенный вдоль совпадающих осей x и x' покоится всистеме K'. Тогда определение его длины в этой системе не доставляет хлопот. Нужно приложить к стержню масштабную линейку и определить координату x'1 одного конца стержня, а затем координату x'2 другого конца. Разность координат даст длину стержня l 0 в системе K': l 0 = x'2 ‑ x'1.
Стержень покоится в системе K'. Относительно системы K он движется со скоростью v, равной относительной скорости систем V.
В системе K дело обстоит сложнее. Относительно этой системы стержень движется со скоростью v, равной скорости V, с которой система K' движется относительно системы K. (Обозначение V мы будем употреблять только применительно к относительной скорости систем отсчета.) Поскольку стержень движется, нужно произвести одновременный отсчет координат его концов x1 и x2 в некоторый момент времени t. Разность координат даст длину стержня l в системе K:
Для сопоставления длин l и l 0 нужно взять ту из формул преобразований Лоренца, которая связывает координаты x, x' и время t системы K, т. е. первую из формул (113). Подстановка в нее значений координат и времени приводит к выражениям
(мы подставили вместо β его значение). Заменив разности координат длинами стержня, а относительную скорость V систем K и K' равной ей скоростью стержня v, с которой он движется в системе K, придем к формуле
Относительность одновременности. Пусть в системе К в точках с координатами x1 и x2 в моменты времени t1 и t2 происходят два события. В системе К' им соответствуют координаты x'1 и x'2 и моменты времени t'1 и t'2. Если события в системе К происходят в одной точке (x1 = x2) и являются одновременными (t1 = t2), то, согласно преобразованиям Лоренца.
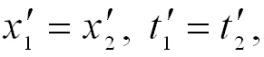
Т.е. эти события являются одновременными и пространственно совпадающими для любой инерциальной системы отсчета. Если события в системе К пространственно разобщены (x1 ≠ x2), но одновременны (t1 = t2), то в системе К', согласно преобразованиям Лоренца.

Таким образом, в системе К' эти события, оставаясь пространственно разобщенными, оказываются и неодновременными.
Длительность событий в разных системах отсчёта
Длительность событий в разных системах отсчета. Пусть в некоторой точке A с координатой x, покоящейся относительно системы К, происходит событие, длительность которого (разность показаний часов в конце и начале события) τ = t2 - t1, где индексы 1 и 2 соответствуют началу и концу события. Длительность этого же события в системе К'.

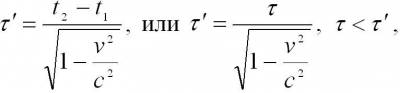
Т.е. длительность события, происходящего в некоторой точке, наименьшая в той инерциальной системе отсчета, относительно которой эта точка неподвижна.
Пример:
Следовательно, часы, движущиеся относительно инерциальной системы отсчета, идут медленнее покоящихся часов, т.е. ход часов замедляется в системе отсчета, относительно которой часы движутся.
Читайте также:

