Дирихле принцип начальная школа

Обновлено: 05.07.2024

Для учеников 1-11 классов и дошкольников
Бесплатные сертификаты учителям и участникам

Принцип Дирихле, задачи на принцип Дирихле

У математиков встречаются весьма странные "принципы", которыми они никогда не поступаются. Впрочем, любой здравомыслящий человек, ознакомившись с этими принципами, вынужден их признать. Вот, например, так называемый принцип Дирихле . Математики очень любят объяснение этого принципа сводить к примеру кроликов в клетках. Поступим так же и мы.

Если в ста (или n) клетках сидит не менее 101 (или n+1) кроликов, то хотя бы в одной клетке находится более одного кролика. Удивительно, что на основе такого простого и даже чуть наивного принципа математикам удается решать весьма трудные задачи, доказывать красивые теоремы, причем не только элементарные.

Докажите, что никакая прямая не может пересекать все три стороны треугольника.

Грани куба окрашены в 2 цвета. Докажите, что найдутся две соседние одноцветные грани.

Имеется 25 конфет 3 сортов. Верно ли, что не менее 9 из них будут какого-то одного сорта?

Утверждение можно доказать, проводя сразу рассуждения от противного. Пусть конфет каждого сорта не более 9, то есть не превышает восьми. Тогда всего конфет не больше 3 × 8 = 24, а по условию их 25. Противоречие.

В классе 30 человек. Паша сделал 13 ошибок, а остальные меньше. Доказать, что какие-то три ученика сделали одинаковое количество ошибок.

В квадратном ковре со стороной 1 м моль проела 51 дырку (дырка — точка). Докажите, что некоторой квадратной заплаткой со стороной 20 см можно закрыть не менее трёх дырок.

Решение: Весь ковер можно накрыть такими 25-ю заплатами. По принципу Дирихле какая-то из этих заплат накроет не менее трех дырок.

Несколько футбольных команд проводят турнир в один круг. Докажите, что в любой момент турнира найдутся две команды, сыгравшие к этому моменту одинаковое число матчей.

Решение: Пусть всего n шахматистов. Тогда каждый мог сыграть от 0 до n - 1 партий: всего n вариантов. Казалось бы, что принцип Дирихле не работает: у нас имеется n различных шахматистов и n различных количеств сыгранных партий.

Заметим, однако, что если какой-то шахматист не сыграл ни одной партии, то не найдется шахматиста, сыгравшего все партии. То есть не может быть ситуации, когда есть игрок, сыгравший 0 партий, и игрок, сыгравший n - 1 партию. Значит, различных количеств сыгранных партий в любой момент турнира может быть не более n - 1 (от 0 до n - 2 или от 1 до n - 1). По принципу Дирихле в любой момент турнира найдется два игрока, сыгравших одинаковое количество партий.

100 человек сидят за круглым столом, причем более половины из них — мужчины. Докажите, что какие-то двое мужчин сидят друг напротив друга.

В клетках таблицы 3 × 3 3×3 расставлены числа − 1 −1 , 0, 1. Докажите, что какие-то две из восьми сумм по всем строкам, всем столбцам и двум главным диагоналям будут равны.

РЕШЕНИЕ

Каждая из этих восьми сумм может принимать лишь семь разных значений: от − 3 −3 до 3, значит, по принципу Дирихле какие-то две суммы совпадут.

Перейдем теперь к обобщенному принципу Дирихле. На языке кроликов и клеток его можно записать так:

если в 10 клетках сидит 51 кролик, то по крайней мере в одной клетке сидит не менее 6 кроликов.

ДОКАЗАТЕЛЬСТВО

Доказательство аналогично обычному принципу Дирихле. Действительно, если в каждой клетке сидит менее 6 кроликов, то во всех 10 клетках кроликов не более 50 — противоречие.

Имеется 101 пуговица одного из 11 цветов. Докажите, что либо среди этих пуговиц найдутся 11 пуговиц одного цвета, либо 11 пуговиц разных цветов.

РЕШЕНИЕ

Предположим, что среди данных пуговиц нет 11 пуговиц разных цветов. Тогда каждая пуговица окрашена в один из 10 цветов. Если пуговиц каждого цвета не более 10, то всего пуговиц не более 100, и это противоречит условию. Таким образом, пуговиц какого-то одного цвета не менее 11, что и нужно было доказать.

Докажите, что из любых семи натуральных чисел можно выбрать три числа, сумма которых делится на 3.

РЕШЕНИЕ

По принципу Дирихле из семи чисел можно выбрать три, дающие одинаковые остатки при делении на 3 (так как имеется лишь три различных остатка — 0, 1 и 2). Их сумма, очевидно, делится на 3.

Докажите, что из любых пяти натуральных чисел можно выбрать три числа, сумма которых делится на 3.

РЕШЕНИЕ

Если среди пяти чисел присутствую все три числа, которые дают различные остатки при делении на 3, то мы найдем три числа, которые в сумме дают число делящееся на 3. Поэтому мы будем считать, что среди наших пяти чисел встречаются числа, дающие всего два различных остатка. Значит, по принципу Дирихле из пяти чисел можно выбрать три, дающие одинаковые остатки при делении на 3 (так как имеется лишь два различных остатка среди наших пяти чисел). Их сумма, очевидно, делится на 3.

Факультатив по математике для 4 класса. Тема: Принцип Дирихле

Ход занятия

Учитель. Если 101 кролика рассадить в 100 клеток, то по крайней мере в одной клетке будет 2 кролика. Понятно почему: ведь в худшем случае, если бы в каждой клетке сидело не больше одного кролика, в 100 клетках их было бы не больше 100.

А если бы было 35 клеток и 743 кролика, то можно было бы утверждать, что даже в худшем случае, если бы в каждой клетке сидело по 21 кролику, еще 8 кроликов резвилось бы на свободе. Следовательно, если рассадить всех кроликов, то по крайней мере в одной клетке будет сидеть не меньше 22 кроликов.

Эти подсчеты с кроликами и клетками в действительности связаны с важным математическим утверждением - принципом Дирихле.

Задача 1. В школе 20 классов. В ближайшем доме живет 23 ученика этой школы. Можно ли утверждать, что среди них обязательно найдутся хотя бы 2 одноклассника?

Даже если считать, что в худшем случае в каждом классе учится по 1 ученику, живущему в ближайшем доме, то останется еще 3 ученика, каждый из которых учится вместе с кем-то из уже имеющихся в классе, то есть найдется класс, в котором будет 2 ученика из соседнего дома.

Задача 2. В школе учится 370 человек. Докажите, что среди всех учащихся найдутся 2 человека, празднующих свой день рождения в один и тот же день. (Решается учащимися самостоятельно.)

Задача 3. Коля подсчитал, что за день в завтрак, обед и ужин он съел 10 конфет. Докажите, что хотя бы один раз он съел не меньше четырех конфет. (Решается учащимися самостоятельно.)

Задача 4. В классе 37 человек. Докажите, что среди них найдутся 4 человека, родившиеся в один и тот же месяц.

В худшем случае в каждом из 12 месяцев родилось по 3 человека - всего 36 человек. 37-й родился с какой-то из этих троек в один месяц.

Задача 5. В коллекции имеется 25 монет по 1, 2, 3, 5 копеек. Имеется ли среди них 7 монет одинакового достоинства? (Решается учащимися самостоятельно.)

Задача 6. Пять мальчиков собрали вместе 14 грибов, причем каждый нашел хотя бы один гриб. Докажите, что хотя бы два мальчика нашли одинаковое число грибов.

В худшем случае у пяти мальчиков могло быть различное число грибов, а всего 1+2 + 3 + 4 + 5 = 15. Но грибов было 14, следовательно, кто-то один, кроме первого, нашел на один гриб меньше. Тогда найдутся 2 мальчика, которые нашли одинаковое число грибов.

Задача 7. Учительница объявила результаты диктанта. Больше всех ошибок было у Пети - 13.

Докажите, что среди 28 учащихся, допустивших ошибки, найдутся 3 человека с одинаковым числом ошибок.

Наибольшее число учащихся, имеющих разное число ошибок, - 13 (от 1 до 13). Если бы одинаковое число ошибок имели по 2 человека, то их было бы 2 • 13 = 26.

Из 28 учащихся найдутся трое, имеющих одинаковое число ошибок.

Задача 8. В первенстве по футболу участвует 18 команд. Первенство разыгрывается в один круг, любые две команды встречаются только один раз. Известно, что каждая команда сыграла какое-то число игр. Докажите, что найдутся две команды, сыгравшие одинаковое число игр. (Решается учащимися самостоятельно.)

Задача 9. В городе живет 200 тыс. жителей. Докажите, что в городе найдутся хотя бы 2 человека с одинаковым числом волос на голове, если считать, что у человека на голове не больше 150 тыс. волос. (Решается учащимися самостоятельно.)

Задача 10. В классе 25 учащихся. Из них 20 занимаются английским языком, 17 увлекаются плаванием, 14 посещают математический кружок. Докажите, что хотя бы один ученик занимается всем этим вместе.

Занимаются английским и увлекаются плаванием не меньше 20 + 17 - 25 = 12 человек, кроме них в классе не больше 25 — 12=13 человек, а посещают математический кружок 14, значит, в классе найдется хотя бы один ученик, который и занимается английским языком, и увлекается плаванием, и посещает математический кружок.

Образовательная цель: познакомить учащихся с новыми математическим методом решения задач, которые не рассматриваются в школьном курсе, научить решать задачи с помощью принципа Дирихле; показать его применение для решения разнообразных задач.

Развивающая цель: развитие у учащихся познавательного интереса, логического мышления; внимания, наблюдательности, накопление определенного запаса математических фактов и сведений, умений и навыков, дополняющих и углубляющих знания, приобретаемые в основном курсе математики.

Воспитательная цель: воспитывать устойчивый интерес к предмету.

Оборудование: мультимедийный проектор, компьютер.

Формулировка темы и целей урока.

Изучение нового материала (презентация).

Учитель: При решении различных математических задач применяется специальный метод, получивший название: принцип Дирихле.

Дирихле родился в вестфальском городе Дюрене в семье почтмейстера. В 12 лет Дирихле начал учиться в гимназии в Бонне, спустя два года в иезуитской гимназии в Кёльне, где в числе прочих преподавателей его учил Георг Ом. С 1822 по 1827 г. жил в качестве домашнего учителя в Париже, где вращался в кругу Фурье. - В 1827г. устраивается на должность приватдоцента университета Бреслау (Вроцлав). В 1829 г. он перебирается в Берлин, где проработал непрерывно 26 лет, сначала как доцент. Затем с 1831 г. Как экстраординарный профессор. С 1839 г. как ординарный профессор Берлинского университета. В 1855 г. Дирихле становится качестве преемника Гаусса профессором высшей математики в Гёттингенском университете

Основные заслуги П. Дирихле в области математики:

— установил, что в арифметической прогрессии аn = а1 + dn, где n = 1,2 . с целыми взаимно простыми а1 и d содержится бесконечно много простых чисел;

— исследовал понятие условной сходимости ряда, установил признак сходимости ряда;

— ввёл функциональные ряды особого вида;

— ввёл (вместе с Н. И. Лобачевским) определение функции через соответствие и т.д.

В комбинаторике принцип Дирихлем (нем. Schubfachprinzip, “принцип ящиков”) — утверждение, сформулированное немецким математиком Дирихле в 1834 году, устанавливающее связь между объектами (“кроликами”) и контейнерами (“клетками”) при выполнении определённых условий. В английском и некоторых других языках утверждение известно как “принцип голубей и ящиков” (англ. Pigeonhole principle), когда объектами являются голуби, а контейнерами — ящики.

Если m кроликов рассажены в n клеток, то хотя бы в одной клетке находится не менее кроликов, а также хотя бы в одной клетке находится не более кроликов.

Первичное закрепление знаний

Рассмотрим примеры различных задач, решаемых с помощью принципа Дирихле.

Задача 1. В классе 15 учеников. Докажите, что найдутся как минимум 2 ученика, отмечающих дни рождения в один месяц.

Пусть 15 учеников будут “зайцы”. Тогда “клетками” будут месяцы года, их 12. Так как 15 > 12, то, по принципу Дирихле, найдется, как минимум, одна клетка, в которой будет сидеть, по крайней мере, 2 “зайца”. То есть, найдется месяц, в котором будут отмечать дни рождения не менее 2 учеников класса.

Задача 2. Внутри равностороннего треугольника со стороной 1 см расположено 5 точек. Докажите, что расстояние между некоторыми двумя из них меньше 0,5 см.

Это наиболее трудная задача на принцип Дирихле . Но на примере ее решения очень хорошо видны все достоинства принципа Дирихле. Итак, при решении сначала надо выбрать что-то за “зайцев”. Так как в условии задачи фигурирует число “5”, то пусть 5 точек будут “зайцами”. Так как “клеток” должно быть меньше, и чаще всего на 1, то их должно быть 4. Как получить эти 4 “клетки”? Так как в условии задачи есть еще 2 числа; 1 и 0,5; причем второе меньше первого в 2 раза, то можно получить 4 “клетки”, разбив равносторонний треугольник с помощью проведения отрезков, соединяющих середины сторон. Тогда получим 4 равносторонних треугольника со сторонами по 0,5 см, которые и будут у нас “клетками”. Так как “зайцев” - 5, “клеток” - 4 и 5>4,то, по принципу Дирихле, найдется “клетка” - равносторонний треугольник со стороной 0,5 см, в который попадут не менее двух “зайцев” - точек. Так как 4 треугольника равны и расстояние между точками в любом треугольнике меньше, чем 0,5 см. т.е. некоторыми двумя точками из пяти расстояние будет меньше, чем 0,5.

Задача 3. Дано 12 целых чисел. Докажите, что из них можно выбрать 2, разность которых делится на 11.

Примем числа за “зайцев”. Так как их 12, то “клеток” должно быть меньше. Пусть “клетки” —это остатки от деления целого числа на 11. Всего “клеток” будет 11: О, 1, 2, 3, 4, 5, 6, 7, 8, 9,10. Тогда, по принципу Дирихле, найдется “клетка”, в которой будут сидеть не менее чем 2 “зайца”, то есть найдутся 2 целых числа с одним остатком. А разность двух чисел с одинаковым остатком от деления на 11, будет делиться на 11.

Материал содержит подробную методическую разработку занятия математического кружка по данной теме, апробированную автором. Тема является одной из востребованных при обучению учащихся решению олимпиадных задач.

Вложение	Размер
zanyatie_matematicheskogo_kruzhka_po_teme_princip_dirihle.doc	60 КБ

Предварительный просмотр:

Образовательная цель: познакомить учащихся с принципом Дирихле и типами задач, решаемых этим методом
Развивающая цель: через решение задач с помощью метода Дирихле развивать умение анализировать, синтезировать, обобщать
Воспитательная цель: посредством организации занятия воспитывать усидчивость, настойчивость в достижении цели, интерес к математике.

Вступительная беседа
Объяснение нового материала
Закрепление
Итог занятия
Малая олимпиада
Домашнее задание

Что отличает урок математики от других уроков? Книгу по математике от книг по какому-то другому предмету? Большое количество вычислений? Формул? Но они есть и в других учебниках: в естествознании, физике, химии, астрономмии. Наличие доказательств – вот что прежде всего отличает математику от других областей знания. Конечно, доказательства встречаются и в других сферах человеческой деятельности, например, в юриспруденции. Однако математические доказательства убедительнее тех, которые можно слышать в суде. Математичекие доказательства признаются эталоном бесспорности.

Что же такое доказательство в математике? Доказательство – это такое рассуждение, которое убеждает нас настолько, что мы готовы убеждать других, используя то же рассуждение. В математике большое значение имеют так называемые доказательства существования. Самый простой способ доказатьсуществование объекта с заданными свойствами – это указать его и, разумеется, убедиться, что он обладает нужными свойствами. Например, чтобы убедиться, что уравнение имеет решение, достаточно привести какое-либо его решение. Такие доказательства называются прямыми. Но бывают и косвенные доказательства, когда обоснование того, что объект существует, происходит без прямого указания на сам объект.

Объяснение нового материала.

Рассмотрим пример. В классе 34 ученика. Докажите, что среди них обязательно найдутся по крайней мере два ученика, у которых фамиля начинается с одной буквы.

Доказательство простое. В русском языке алфавит содержит 33 буквы. Предположим, что нет таких учеников, у которых бы фамилия начиналась с одной буквы. Тогда учеников должно быть не более 33, а их 34.

Логический прием, который был использован прирешении этой задачи, называется принципом Дирихле. Дирихле Петер Август Лежен (1805-1859) – немецкий математик, иностранный член Петербургской Академии наук, член многих академий. Дирихле –автор многих достижений в области математики, одна из его заслуг – принцип доказательства, названный его именем.

Например, если 4 кролика разместить в 3 клетках, то найдется хотя бы одна клетка, в которой будет не менее 2 кроликов (сделать рисунок). Предположим, что не существует клетки, где сидят два кролика. Тогда в трех клетках окажется не более 3 кроликов (сделать рисунок), а их 4 – противоречие.

Запишем принцип Дирихле: если по N разложить предметы,число которых M больше N, то найдется ящик, в котором будет находится больше одного предмета.

Вернемся к первой задаче. Что в ней предметы? (ученики, M=34). Что в ней ящики? (количество букв в алфавите, N =33). M>N, то по принципу Дирихле хотя бы на одну букву будет приходится две фамилии.

Вернемся ко второй задаче. Что в ней предметы? (кролики, M= 4). Что в ней ящики? (клетки, N=3).M>N, то по принципу Дирихле хотя бы в одной клетке окажется два кролика.

1.В мешке лежат шарики двух разных цветов.Какое наименьшее число шариков нужновынуть из мешка, чтобы среди ни обязательно оказались два шарика одного цвета?

Здесь роль предметов играют шарики (М=?), роль ящиков - цвета (N=2).Чтобы M>N, т.е. в одном ящике оказалось два предмета, их должно быть больше двух, т.е. М=3

2.В коробке лежат карандаши: 7 красных и 5 синих. В темноте берут карандаши. Сколько карандашей надо взять, чтобы среди них было не менее 2 красных и не менее 3 синих?

3.В мешке лежат 10 черных и 10 белых шаров. Они тщательно перемешены и неразлечимы на ощупь. Какое наименьшеее количество шаров нужно вынуть из мешка, чтобы среди них наверняка оказались два шара 1) одного цвета, 2)разного цвета, 3) белого цвета.

Решение:1)Если предположить, что предметы – шарики, которые нужно взять (М=?), а количество ящиков - цвета N=2, то по принципу Дирихле М=3

2)если предположить, что сначала будут попадаться шары только одного цвета, то N=10,следовательно, М=11

3)если предположить, что все время будут попадаться шары черного цвета, то М=12.

4.При каком наименьшем количестве учеников школы среди них обязательно найдутся двое, у которых день и месяц рождения совпадают?

Решение: Дней в году N=365 или 366,то принципу Дирихле М= 366 или 367.

5.В лесу растет миллион елок. Известно, что на каждой из них не более 600 000 иголок. Докажите, что в лесу найдутся хотя бы две елки с одинаковым числом иголок.

6.В городе Санкт-Петербурге живет более 4млн. человек. Докажите, что у каких-то двух из них одинаковое количество волос на голове, если известно, что у любого человека на голове не более миллиона волос.

Решение: Если предположить, что у всех людей разное количество волос, то таких людей N=1000 000 (ящики), а по условию людей М=4 000 000. М>N, то по принципу Дирихле найдутся хотя бы два человека в одинаковым количеством волос.

3 тип. Обобщенный принцип Дирихле: если по N ящикам разложить предметы, число которых М больше, чем N (где к – натуральное число), то найдется ящик, в котором находятся более к предметов.

7.В магазин привезли 25 ящиков с яблоками трех сортов, причем в каждом ящике лежали яблоки какого-то одного сорта. Можно ли найти 9 ящиков с яблоками одного сорта?

Решение. 25:3=8 (ост.1). 25=8*3+1. к=3, N=8, M>N, то принципу Дирихле найдутся хотя бы один ящик, в котором находятся более, чем к=3 предметов, т.е. 4 предмета.

8.На площадке 20 собак восьми разных пород. Докажите, что среди них есть не менее трех собак одной породы.

Решение: 20:8=2(ост. 4), 20=8*2+4. к=2,N=8, М>N, то по принципу Дирихле найдутся хотя бы три собаки одной породы.

9.В классе 27 учеников. Найдется ли месяц, в котором отмечают свои дни рождения не меньше, чем три ученика этого класса?

Решение: В году 12 месяцев. 27:12=2(ост.3), 27=12*2+3. к=2,N=12,M>N, то по принципу Дирихле найдутся хотя бы три ученика, у которых дни рождения в одном месяце.

Таким образом, применяя данный метод,необходимо:

3)выбрать для решения требуемую формулировку принципа Дирихле.

1. В ящике лежат носки четырех цветов. Какое наименьшеее количество носков надо вытащить, чтобы из них можно было составить хотя бы одну пару?

Решение: N=4 (это количество цветов), То М=5.

2.В темной кладовой лежат ботинки одного размера: 10 пар черных и 10 пар коричневых. Найдите наименьшее число ботинок, которое нужно взять из кладовой,чтобы среди них оказалась хотя бы одна пара (левый и правый) одного цвета. В темноте нельзя определить не только цвет ботинок, но и левой от правого.

Решение: Если предположить (худший вариант), что подряд попадаются ботинки на одну ногу (20), а затем ботинок на другую ногу, то20+1=21, среди них будут ботинки на одну ногу.

3.В школе учится 1200 учеников. Найдется ли день, в который отмечают свои дни рождения не меньше, чем 4 ученика данной школы?

Решение: 1200:366 =3(ост. 102),к = 3, N=366-количество дней в високосном году, M>N, то по обощенному принципу Дирихле найдутся хотя бы 4>к ученика, у которых дни рождения в один день.

4.В классе 26 учеников, из них более половины мальчики. Докажите, что какие-то 2 мальчика сидят за одним столом (в классе 13 столов).

Решение: Мальчиков более половины, т.е. более 13, М>13, то М :13=1(остатка есть), М=13*1+ ост, к=1, N=13 – количество столов , то по обощенному принципу Дирихле хотя бы 2 мальчика сидят за одним столом.

1.На дискотеку в студенческое общежитие, в котором 42 комнаты, пришли 36 гостей. Докажите, что найдется комната, в которую не пришел ни один гость.

Решение. Обозначив комнаты как предметы (М), а гостей как ящики (N), получим М>N, то по принципу Дирихле найдутся хотя бы две комнаты, в которые должен был прийти один и тот же гость, т.е.пустые комнаты.

2.В классе 37 учеников. Докажите, что среди них найдутся 4 ученика, отмечающие свой день рождения в одном месяце.

Решение: 37:12=3(ост. 1),37=12*3+1. к=3, N=12-количество месяцев в году. M>N, то по обощенному принципу Дирихле найдется болеек, т.е.более 3,значит,4 ученика с днем рождения в одном месяце.

3. В доме живут 5 кошек. У них 16 котят. Докажите, что хотя бы у одной кошки не менее четырех котят.

Решение. 16:5=3(ост.1), 16=5*3+1. к=3, N=5. M>N, то по обощенному принципу Дирихле найдется хотя бы две кошки, у которых более 3, т.е. не менее 4 котят.

4.В ящике 25 белых шаров, 25 черных, 20 синих и 10 красных. На ощупь шары неотличимы друг от друга. Шары вынимают из ящика в темноте. Какое наименьшее количество шаров нужно вынуть, чтобы среди них обязательно оказалось: 1)10 шаров одного цвета; 2) 10 белых шаров?

Решение: 1)в худшем случае это будут 9 белых шаров+9 черных шаров+9 синих+9 красных=36 шаров. В любом случае, следующий шар будет иметь цвет, который станет 10. М=37.

2)В худшем случае это будут 25 черных + 20 синих + 10 красных + 10 белых шаров =65 шаров.

Задания для решения на занятии

1.В мешке лежат шарики двух разных цветов. Какое наименьшее число шариков нужновынуть из мешка, чтобы среди ни обязательно оказались два шарика одного цвета?

8.На площадке 20 собак восьми разных пород. Докажите, что среди них есть не менее трех собак одной породы.

По теме: методические разработки, презентации и конспекты

Принцип Дирихле

Разработки и решение задач с использованием принципа Дирихле.

Принцип Дирихле и его применение при решении задач.

Очень часто в задания математических олимпиад включаются задачи, при решении которых можно использовать прием, называемый принципом Дирихле. В шко.

Принцип Дирихле. Решение олимпиадных задач. Первое занятие

Материал предназначен для подготовке к олимпиаде.

Решение олимпиадных задач ,используя принцип Дирихле второе занятие

Данный материал можно использовать в рамках подготовки учащихся к олимпиаде, как дополнительный материал на кружках и элективных занятиях.

Тема самообразования "Принцип Дирихле".

Одна из главных задач педагога, обучающего детей с нарушениями зрения, является необходимость найти и применить все возможные педагогические методы и приёмы для оказания психолого-педагогической помощ.

Применение принципа Дирихле при решении задач ЕГЭ.

Разбор задач ЕГЭ.

Занятие кружка. Принцип Дирихле.

На занятии кружка рассмотрен сам принцип Дирихле. Показала как он работает. Разобрали олимпиадные задачи.

В математике существует множество принципов. Некоторые из них достаточно просты и понятны даже новичку, а некоторые требуют определенных объяснений и доказательств. Однако все они весьма эффективны, и их легко можно применять на практике. Одним из них является принцип Дирихле (известный также как принцип голубей/кроликов). Это достаточно простое утверждение, способное помочь в решении многих математических задач.

История

Современная формулировка и доказательство

На сегодняшний день существует несколько разных формулировок данного принципа. Самая понятная и простая подразумевает, что нельзя посадить 8 кроликов в 3 клетки так, чтобы в каждой было не больше 2. Более научная и сложная формулировка, объясняющая принцип Дирихле, гласит: если в k ячеек находится k+1 зайцев, то, по крайней мере, в 1 ячейке будет располагаться больше одного зайца. А если в k ячеек находится k-1 зайцев, то по крайней мере в 1 ячейке будет располагаться меньше одного зайца. Доказательство этого утверждения совсем простое, так сказать, от противного. Если предположить, что в каждой ячейке располагается зайцев меньше, чем k-1/k, тогда в k ячеек зайцев меньше чем k*k-1/k = k-1, а это противоречит первоначальным условиям.

В действительности такой простой и понятный принцип значительно облегчает решение задач по математике и доказательства многих трудоемких теорем. Просто необходимо учитывать, что зайцев и ячейки можно легко заменить на математические предметы и объекты (цифры, точки, отрезки, фигуры и т. д.).

Еще одна формулировка

Иногда задачи на принцип Дирихле - не такие простые и очевидные, как с животными в ящиках. Необходимо переносить этот принцип на математические множества, чтобы отыскать какие-либо решения. В таком случае можно опираться на другую, более сложную формулировку.

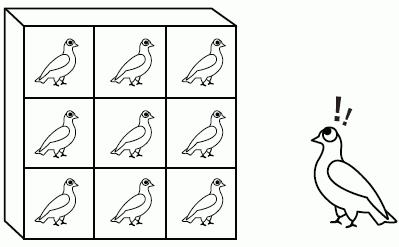
Если отобразить множество S, содержащее d+1 элементов, в множество R с совокупностью d элементов, то два элемента из множества S будут иметь одинаковый образ.

Хотя современные ФГОС по математике предъявляют к ученикам творческие требования и предлагают нестандартные варианты, решение через утверждение Дирихле не всегда такое простое и понятное. Иногда очень трудно определить, какую величину считать животным, а какую – клеткой, и каким образом факт наличия двух животных в одной клетке поможет решению задачи. Да и если удастся в этом разобраться, все равно нельзя определить, в какой именно клетке будет находиться объект. То есть можно просто доказать существование такой ячейки, но нельзя конкретизировать ее.

Пример № 1. Геометрия

Современные примеры решения задач демонстрируют, что животными и клетками могут выступать совершенное различные математические предметы.

Прямая k проходит через плоскость треугольника ABC, однако не пересекает ни одну его вершину. Необходимо доказать, что она не может пересекать три его стороны.

Представим, как прямая k разбивает треугольник на две плоскости, назовем их s1 и s2. Будем считать, что s1 и s2 открытые, то есть не содержащие прямую k. Ну а сейчас - самое время применить принцип Дирихле. Задачи с решениями могут продемонстрировать, что под кроликами и ячейками в современных условиях подразумеваются разнообразные объекты. Так, вместо зайцев мы подставим вершины треугольника, а вместо ячеек – полуплоскости. Поскольку проведенная прямая k не пересекает ни одну из вершин, то каждая из них находится в той или иной плоскости. Но поскольку вершины в треугольнике три, а плоскости у нас всего две (s1 и s2), то одна из них будет содержать две вершины. Предположим, что это вершины A и B, и находятся они в полуплоскости s2 (то есть лежат по одну сторону от k). В таком случае отрезок АВ не пересекает прямую k. То есть в треугольнике есть сторона, которую прямая k не пересекает.

Альтернативное решение

В данной задаче мы предположили, что в одной плоскости находятся точки А и В, однако принцип Дирихле не указывает конкретную ячейку, поэтому точно так же мы могли указать, что в одной плоскости разместились вершины С и В, или А и С. Для данной задачи совсем не важно, какую сторону треугольника не пересекает прямая k. Поэтому указанный принцип идеально подходит для ее решения.

Пример № 2. Геометрия

В середине равностороннего треугольника АВС (у которого АВ = ВС = АС = 1) разместилось 5 точек. Необходимо доказать, что две из них располагаются на расстоянии меньше 0,5.

Если провести в правильном треугольнике АВС средние линии, они разделят его на 4 маленьких правильных треугольника со сторонами ½ = 0,5. Предположим, что эти треугольники – ячейки, а точки внутри них – кролики. Получается, у нас есть 5 кроликов и 4 ячейки, следовательно, в одной из них будет находиться как минимум два кролика. Учитывая то, что точки не являются вершинами (так как они располагаются внутри треугольника АВС, а не на одной из его сторон), они будут размещаться внутри маленьких фигур. Следовательно, расстояние между ними будет меньше, чем 0,5 (поскольку величина отрезка внутри треугольника никогда не превышает величины его самой большой стороны).

Пример № 3. Комбинаторика

В других областях также можно удачно применять принцип Дирихле: комбинаторика и математическая физика уже давно опираются на него при решении задач.

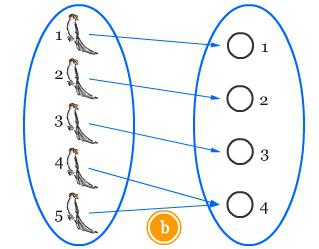
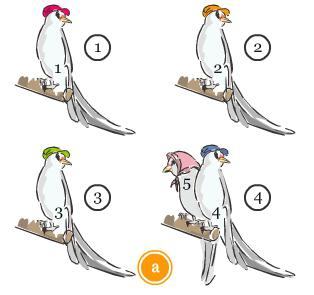
Допустим, вокруг округлённого стола стоят на равном расстоянии друг от друга m флажков разных стран, а за столом сидят m представителей от каждой страны, причем каждый из них расположился рядом с чужим флажком. Нужно доказать, что при определенном вращении стола хотя бы двое из представителей окажутся возле своих флажков.

Получается, что существует m-1 способов развернуть стол так, чтобы изменилось взаиморасположение представителей и флажков (если исключить начальное размещение стола), но при этом остается m представителей.

Приступая к решению такой задачи, важно понимать, что начальное положение – это тоже ячейка, но по условию задачи она заведомо пустует, поэтому мы уменьшаем общее количество на 1 (m-1).

Пример № 4. Теория чисел

Принцип Дирихле в теории чисел также имеет огромное значение.

Предположим, на листике тетради в клетку ученик произвольно в узлах клеточек проставил 5 точек. Необходимо доказать, что как минимум один отрезок с вершинами в этих точках пройдет через узел клеточки.

Для начала нужно изобразить на листе тетради систему координат, основа которой расположится в одном из узлов. Оси системы координат будут совпадать с линиями сетки, а за единичный отрезок принята сторона клеточки. Получается, что все 5 отмеченных точек будут находиться в системе, а их координаты будут только целым числом (четным или нечетным). Таким образом, мы получим 4 варианта координат: (четный; четный), (нечетный; четный), (четный; нечетный) и (нечетный; нечетный). А значит, 2 из 5 точек будут соответствовать одному варианту. Если посмотреть на ситуацию с позиции Дирихле, то необходимо обозначить точки как зайцев, а варианты координат - как ячейки. Мы получаем 5 зайцев и 4 клетки, соответственно, в одной из них будет минимум 2 животных. Допустим, это точки Р и А, с координатами (x₄, y₃) и (x₅, y₆). Середина отрезка, соединяющего эти две вершины, будет иметь координаты ((x₄+x₅) / 2), ((y₃+y₆) / 2)), которые будут целыми числами в условиях соответствующей четности x₄ и x_5, y₃ и y₆. Получается, что середина отрезка расположилась в узле клетки.

Пример № 5

Достаточно много задач разной сложности можно решить через принцип Дирихле. Задачи с решениями разнообразных математических и логических вопросов достаточно часто опираются на этот принцип.

На прямой дороге вырыты маленькие поперечные канавки. Расстояние между всеми канавками одинаковое и равно оно Ö2 м. Необходимо доказать, что, независимо от ширины канавок, человек, шагающий по дороге с интервалом 1 м, однажды попадет ногой в одну из них.

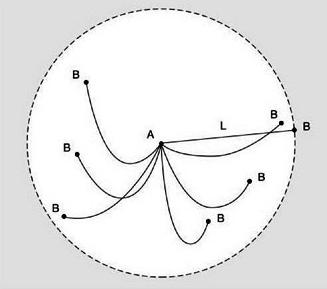
Обобщение принципа

Материалы по математике, кроме стандартных (простых и не очень) формулировок, содержат также одну обобщенную, которая используется для выявления более двух объектов, похожих друг на друга. Она утверждает, что если dm + 1 кроликов поместить в d ячеек, то как минимум m + 1 кролик окажется в одной ячейке.

Пример № 6. Обобщение

Прямоугольник с площадью 5 х 6 клеток (30 клеток), закрашенных только 19. Можно ли обнаружить квадрат площадью 2 х 2 клетки, в котором минимум три будут закрашены?

Нашу фигуру необходимо разделить на 6 блоков по 5 клеток. Исходя из утверждения Дирихле, в одной из них будет закрашено не менее 4 клеточек (19/6 = 4). Тогда в одном из квадратов площадью 4 клеточки, расположенном в одном из блоков, будет закрашено минимум 3 клетки.

Пример № 7

Класс, в котором 25 человек. Из любых случайно выбранных 3 учеников двое будут друзьями. Необходимо доказать, что в классе находится школьник, у которого больше 11 приятелей.

Два решения вопроса

Для начала возьмем двух школьников, которые не дружат с друг другом (поскольку если бы все они дружили между собой, то в каждой тройке было бы три друга и каждый ученик дружил бы с 24 другими). Оставшиеся 23 одноклассника будут дружить с одним из нашей двойки, поскольку в противном случае нашлась бы тройка, где нет друзей (а это противоречит изначальному условию задачи). Получается, что один из двух школьников будет дружить как минимум с 12 учениками. В данном случае ученики – это кролики, а условия "друзья они или нет" – это ячейки. Мы имеем 23 животных и только 2 клетки. Соответственно, в одной из них как минимум 23/2 = 11,5, т. е. 12 кроликов. То есть один из 2 выбранных нами учеников будет дружить как минимум с 12 своими одноклассниками (или даже больше). Конечно же, существуют и другие методы решения задачи, однако данный - один из самых понятных и удобных.

Читайте также: