Числовые характеристики двумерной случайной величины кратко

Обновлено: 05.07.2024

В предыдущих двух статьях (ссылки по тексту) мы рассмотрели двумерную дискретную случайную величину , в том числе с зависимыми компонентами , и теперь перейдём к двумерной непрерывной СВ. Задач запланировано немало, и поэтому сразу начинаем.

Если же компоненты – непрерывны, то непрерывна в любой точке плоскости и её график представляет собой кусочно-гладкую или даже полностью гладкую поверхность, пожалуйста: .

И из вышесказанного следует, что данная функция может принимать значения только из промежутка .

Кроме того, функция распределения обладает ещё одним свойством. Если мы устремим к , то получим:
– не что иное, как функцию распределения вероятностей случайной величины , которая рассматривается отдельно, без случайной величины .

Здесь получились одинаковыми, но в общем случае они, конечно, различны.

Помимо функции , для двумерной непрерывной СВ вводится понятие функции плотности распределения вероятностей, которая определяется как смешанная производная 2-го порядка от функции распределения:

Аналогично одномерному случаю, для функции плотности справедлив следующий факт:
, который означает, что в результате испытания случайная величина достоверно примет одно из своих возможных значений .

Если все возможные пары образуют ограниченную область (как оно часто бывает), то свойство выражается через обычный двойной интеграл по этой области:

…будём проверять свойство для нашего примера? :) Ну, конечно, будем, двойной несобственный интеграл здесь очень прост:

Сначала вычислим внутренний несобственный интеграл. Ввиду чётности подынтегральной функции, интервал интегрирования удобно споловинить, а результат удвоить:
– подставляем во внешний интеграл:
, что и требовалось проверить.

Обратно: как получить функцию , если известна плотность ?
По стандартной формуле:

В качестве разминки найдите – двойной несобственный интеграл с бесконечными нижними пределами и получИте исходную функцию распределения. Одномерный аналог этой задачи рассмотрен в Примере 6 статьи Непрерывная случайная величина.

После чего разберём более содержательное задание, узнаем новые формулы и порисуем заодно:

Непрерывная двумерная случайная величина распределена равномерно в прямоугольнике с вершинами . Требуется:

1) Составить функцию плотности распределения случайной величины и плотности распределений составляющих и .

2) Найти функцию распределения вероятностей .

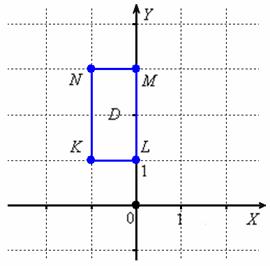
Решение: из условия следует, что случайная величина с равной вероятностью может принять любое значение из области , которая ограничена прямоугольником :

По сути, перед нами двумерная версия равномерного распределения вероятностей, и для нахождения её плотности проще всего разделить единицу на площадь области . Очевидно, что эта площадь равна и искомая функция плотности:

Сразу изобразим график, его сподручнее построить от руки:

Здесь я символически очертил всю плоскость , дабы указать, что функция определена в любой её точке. Убедимся, что мы действительно составили функцию плотности, для этого нужно проверить её характеристическое свойство:

, что и требовалось проверить.
Легко видеть, что двойной интеграл численно равен объёму цилиндрического бруса, в данном случае – параллелепипеда с основанием и высотой

Составим плотности распределения случайных величин и . Для этого есть специальные формулы:
и при иных значениях .

Примечание: поскольку компонента принимает значения лишь из промежутка от 1 до 3, то .

Проверим, что полученные функции действительно являются одномерными плотностями распределения вероятностей:

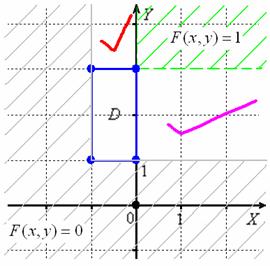
И осталось прояснить ситуацию с областями, отмеченными красной и малиновой галочками:

В области (красный цвет) событие является достоверным, и поэтому функция упрощается до функции распределения по компоненте :
– и не пренебрегаем элементарной проверкой:

В области (малиновый цвет) достоверным становится событие и поэтому:
, контроль:

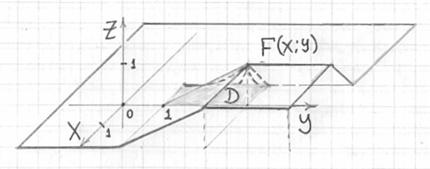
В обоих случаях получены уравнения плоскостей, и я рад представить вам свой небольшой шедевр:

…надо было заснять на веб камеру, глядишь, станет классикой постиндустриальной живописи :)

Таким образом, функция распределения вероятностей:

Обратите внимание, что в нашей задаче справедливо равенство , и это означает, что. скоро узнАем!

3) Вычислим – вероятность того, что случайная величина примет значение из указанной в скобках области. Это можно сделать двумя способами, по формуле:

Второй способ состоит в нахождении двойного интеграла от функции плотности по соответствующей области:

Вероятность вычислим по той же формуле (см. выше), принимая во внимание предельные значения :

И, наконец:
– по той причине, что этому условию удовлетворяют все точки прямоугольника за исключением нижней стороны , но с позиций геометрии её площадь равна нулю, и поэтому данный факт не принимается во внимание. О подобном парадоксе я уже рассказывал, когда мы изучали функцию распределения одномерной случайной величины.

В этой связи, кстати, задача с открытой областью будет решаться аналогично, с той поправкой, что придётся скорректировать строгость неравенств при записи функции плотности распределения.

Возможно, у вас возник вопрос: а почему я не разобрал построение функции распределения для двумерной дискретной СВ? Дело в том, что даже в простых случаях у такой функции получается 10-20 кусков, и поэтому такое задание, как правило, не предлагают для решения. Впрочем, в очень простом случае кусков будет всего 5, и я-то предложу вам маленькую факультативную задачку:

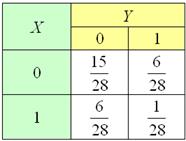
Двумерная дискретная случайная величина задана таблично:

Составить функцию распределения.

Эта СВ взята из демонстрационного примера статьи о зависимых случайных величинах, и если вам совсем трудно, то вспомните её содержательный смысл. Краткое решение совсем близко. Желающие могут построить график, и если он получился удачно – присылайте, опубликую!

И задача для закрепления материала:

Непрерывная двумерная случайная величина задана своей функцией распределения в квадрате и принимает значения только из этой области. Найти:

1) значение параметра ;

2) функцию плотности распределения и проверить, что она является таковой;

3) плотности составляющих , выполнить аналогичную проверку;

Таблица значений тригонометрических функций в помощь. И на всякий случай таблица производных и интегралов, …ну а кому сейчас легко? :) …я и сам как-то опрометчиво предположил, что решение пункта 4 легче провести через интегралы, но оно оказалось явно не легче :) Поэтому, всегда анализируйте, какой способ выгоднее.

Стараемся всё решить самостоятельно – не подглядываем!

Жду вас в заключительной части темы, где мы поговорим о независимости и зависимости двумерной непрерывной случайной величины, её условных законах распределения, математических ожиданиях, дисперсиях и коэффициентах ковариации, корреляции.

Решения и ответы:

Пример 7. Решение:

Если или , то
Если , то
Если , то (вероятности просуммировали по строке)
Если , то (вероятности просуммировали по столбцу)
Если , то

Пример 8. Решение:

1) Так как случайная величина принимает значения только из указанного квадрата, то значение функции распределения в его правом верхнем углу должно равняться единице:
, откуда следует:

2) Функцию плотности распределения найдём по формуле . В данном случае:

Таким образом, , если и при иных значениях аргументов.

Проверим выполнение свойства . В данном случае этот интеграл равен:

, что и требовалось проверить.

3) Найдём плотности распределения составляющих:

Контроль:

, что и требовалось проверить.

4) Искомые вероятности вычислим с помощью двойных интегралов от функции плотности по соответствующим областям:

Автор: Емелин Александр

(Переход на главную страницу)

cкидкa 15% на первый зaкaз, при оформлении введите прoмoкoд: 5530-hihi5

При изучении двумерных случайных величин рассматриваются числовые характеристики составляющих:

, , , , где

для дискретных составляющих X и Y и

в случае непрерывных составляющих.

Упорядоченную пару чисел называют математическим ожиданием двумерной случайной величины, а - ее дисперсия.

Отмеченные выше числовые характеристики не определяют степень зависимости составляющих X и Y. Эту роль выполняют корреляционный момент (иначе: ковариация ), который определяется следующим образом:

. (6.2.3)

Для дискретных случайных величин

(6.2.4)

Для непрерывных случайных величин

(6.2.5)

Корреляционный момент можно вычислить по формуле (6.2.6)

. (6.2.6)

Если Х и Y независимы, то . Если , то Х и Y зависимые случайные величины.

В случае случайные величины X и Y называют некоррелированными, при этом она могут быть как зависимыми, так и независимыми.

Ковариация X и Y характеризует не только степень зависимости случайных величин, но и их рассеяние вокруг точки . Кроме того, - размерная величина, что затрудняет ее использование для оценки степени зависимости для различных случайных величин.

Для оценки зависимости вводится коэффициент корреляции

, (6.2.7) где и - среднеквадратические отклонения X и Y.

Коэффициент корреляции - безразмерная величина, обладающая следующими свойствами:

1. - ограниченная величина, а именно .

2. Если X и Y – независимые случайные величины, то .

3. Если X и Y связаны линейной функциональной зависимостью , то и наоборот.

Из последнего свойства можно сделать вывод: коэффициент корреляции характеризует степень линейной зависимости случайных величин X и Y.

Пример 6.2.1.В урне содержится 4 белых и 2 черных шара. Из нее извлекают 2 шара без возвращения. Пусть X – число извлеченных белых шаров, Y – число извлеченных черных шаров. Составить закон совместного распределения двумерной случайной величины и найти коэффициент корреляции .

Решение. Как Х, так и Y могут принимать значения 0; 1; 2. Вычислим соответствующие вероятности.

, , .

X Y

0,4

Очевидно, что ,

Составим распределения X и Y.

X
p_i			0,4

Y
p_j	0,4

Найдем , .

Вычислим .

Вычислим и .

Вычислим .

Следовательно, Х и Y связаны линейной зависимостью.

Пример 6.2.2. Плотность совместного распределения случайных величин Х и Y задана формулой

Найти: 1) коэффициент с; 2) безусловные и условные плотности распределения Х и Y; 3) , ; 4) ковариацию Х и Y.

Решение. Так как , то вычислив = , получим и .

Найдем и

Условный закон распределения Х

Вычислим и .

Аналогично .

Вычислим .

При изучении двумерных случайных величин рассматриваются числовые характеристики составляющих:

, , , , где

для дискретных составляющих X и Y и

в случае непрерывных составляющих.

Упорядоченную пару чисел называют математическим ожиданием двумерной случайной величины, а - ее дисперсия.

. (6.2.3)

Для дискретных случайных величин

(6.2.4)

Для непрерывных случайных величин

(6.2.5)

Корреляционный момент можно вычислить по формуле (6.2.6)

. (6.2.6)

Если Х и Y независимы, то . Если , то Х и Y зависимые случайные величины.

Для оценки зависимости вводится коэффициент корреляции

, (6.2.7) где и - среднеквадратические отклонения X и Y.

Коэффициент корреляции - безразмерная величина, обладающая следующими свойствами:

1. - ограниченная величина, а именно .

2. Если X и Y – независимые случайные величины, то .

3. Если X и Y связаны линейной функциональной зависимостью , то и наоборот.

Решение. Как Х, так и Y могут принимать значения 0; 1; 2. Вычислим соответствующие вероятности.

, , .

X Y

0,4

Очевидно, что ,

Составим распределения X и Y.

X
p_i			0,4

Y
p_j	0,4

Найдем , .

Вычислим .

Вычислим и .

Вычислим .

Следовательно, Х и Y связаны линейной зависимостью.

Пример 6.2.2. Плотность совместного распределения случайных величин Х и Y задана формулой

Найти: 1) коэффициент с; 2) безусловные и условные плотности распределения Х и Y; 3) , ; 4) ковариацию Х и Y.

Решение. Так как , то вычислив = , получим и .

Найдем и

Условный закон распределения Х

Вычислим и .

Аналогично .

Вычислим .

Ранее мы разобрали примеры решений задач для одномерной дискретной случайной величины. Но бывает, что результат испытания описывается не одной, а несколькими случайными величинами (случайным вектором).

В случае двух величин (скажем, $X$ и $Y$) мы имеем дело с так называемой двумерной дискретной случайной величиной $(X,Y)$ (или системой случайных одномерных величин). Кратко выпишем основы теории.

Система двух случайных величин: теория

Двумерная ДСВ задается законом распределения (обычно представленным в виде таблицы распределения):

$$ P(X=x_i, Y=y_k)=p_, i=1,2. m; k=1,2. n; \quad \sum_p_=1. $$

По нему можно найти одномерные законы распределения (составляющих):

$$ p_i=P(X=x_i)=\sum_p_, i=1,2. m; \\ p_k=P(Y=y_k)=\sum_ p_, k=1,2. n. $$

Интегральная функция распределения задается формулой $F(x,y)=P(X\lt x, Y\lt y)$. Даже для самого простого закона распределения 2 на 2 функция занимает 5 строк, поэтому ее редко выписывают в явном виде.

Если для любой пары возможных значений $(X=x_i, Y=y_k)$ выполняется равенство

$$P(X=x_i, Y=y_k)=P(X=x_i)\cdot P(Y=y_k),$$

то случайные величины $X, Y$ называются независимыми.

Если случайные величины зависимы, для них можно выписать условные законы распределения (для независимых они совпадают с безусловными законами):

Для случайных величин $X,Y$, входящих в состав случайного вектора, можно вычислить ковариацию и коэффициент корреляции по формулам:

Далее вы найдете разные примеры задач с полным решением, где используются дискретные двумерные случайные величины (системы случайных величин).

Примеры решений

Задача 1. В продукции завода брак вследствие дефекта А составляет 10%, а вследствие дефекта В - 20%. Годная продукция составляет 75%. Пусть X - индикатор дефекта А, a Y - индикатор дефекта В. Составить матрицу распределения двумерной случайной величины (X, Y). Найти одномерные ряды распределений составляющих X и У и исследовать их зависимость.

Задача 2. Два баскетболиста по два раза бросают мяч в корзину. При каждом броске вероятность попадания для первого баскетболиста 0,6, для второго – 0,7. Случайная величина X – число попаданий первым баскетболистом по кольцу. Случайная величина Y – суммарное число попаданий обоими баскетболистами. Построить таблицу распределения случайного вектора (X,Y). Найти характеристики вектора (X,Y). Зависимы или независимы случайные величины X и Y.

Задача 3. Слово РОССИЯ разрезано по буквам. Случайным образом вынимаем две буквы, тогда X – количество гласных среди них, затем вынимаем еще две буквы и Y – количество гласных во второй паре. Составить закон распределения системы случайных величин X, Y.

Задача 4. $X, Y$ - индикаторы событий $A, B$, означающий положительные ответы соответственно на вопросы $\alpha, \beta$ социологической анкеты. По данным социологического опроса двумерная случайная величина $(X,Y)$ имеет следующую таблицу распределения.
Положительному ответу присвоен ранг 1, отрицательному – 0.
Найти коэффициент корреляции $\rho_$.

Задача 5. Составить закон распределения X - сумм очков и Y - числа тузов при выборе двух карт из колоды, содержащей только тузов, королей и дам (туз=11, дама=3, король=4)
Найти законы распределения величин Х и Y. Зависимы ли эти величины? Написать функцию распределения для (Х, Y). Построить ковариационный граф. Посчитать ковариацию (X,Y). Написать ковариационную матрицу. Посчитать корреляцию (X,Y) и написать корреляционную матрицу.

Задача 6. Бросаются две одинаковые игральные кости. Случайная величина X равна 1, если сумма выпавших чисел четна, и равна 0 в противном случае. Случайная величина Y равна 1, если произведение выпавших чисел четно, и 0 в противном случае. Описать закон распределения случайного вектора (X,Y). Найти D[X], D[Y] и cov[X,Y].

Задача 7. В урне лежат 100 шаров, из них 25 белых. Из урны последовательно вынимают два шара. Пусть $X_i$ – число белых шаров, появившихся при $i$-м вынимании. Найти коэффициент корреляции между величинами $X_1$ и $X_2$.

Задача 8. Для заданного закона распределения вероятностей двухмерной случайной величины (Х, Y):
Y\X 2 5
8 0,15 0,10
10 0,22 0,23
12 0,10 0,20
Найти коэффициент корреляции между величинами Х и Y.

Задача 9. Задана дискретная двумерная случайная величина (X,Y).
А) найти безусловные законы распределения составляющих;
Б) построить регрессию случайной величины Y на X;
В) построить регрессию случайной величины X на Y;
Г) найти коэффициент ковариации;
Д) найти коэффициент корреляции.
20 30 40 50 70
3 0,01 0,01 0,02 0,02 0,01
4 0,04 0,3 0,06 0,03 0,01
5 0,02 0,03 0,06 0,07 0,05
9 0,05 0,03 0,04 0,02 0,03
10 0,03 0,02 0,01 0,01 0,02

Задача 10. Система (x, y) задана следующей двумерной таблицей распределения вероятностей. Определить:
А) безусловные законы распределения составляющих;
Б) условный закон распределения y при x=1;
В) условное математическое ожидание x при y=2.
Г) вероятность того, что случайная величина (x,y) будет принадлежать области $|x|+|y|\le 3$.
-3 0 2
-1 0 0,1 0,15
1 0,05 0,3 0,05
2 0,15 0,05 0,15

Перед тем, как ввести определения и формулы вычисления основных числовых характеристик системы двух случайных величин напомним, что такое закон распределения.

Законом распределения двумерной случайной величины $(X,Y)$ - называется множество возможных пар чисел $(x_i,\ y_j)$ (где $x_i \epsilon X,\ y_j \epsilon Y$) и их вероятностей $p_$.

Чаще всего закон распределения двумерной случайной величины записывается в виде таблицы (Таблица 1).

Рисунок 1. Закон распределения двумерной случайной величины.

Введем для начала еще два обозначения:

Изобразим теперь дополненную таблицу распределения двумерной случайной величины (таблица 2).

Рисунок 2. Дополненная таблица закона распределения двумерной случайной величины.

Условие нормированности для двумерной случайной величины

Введем для начала условие, которое обязательно должно выполняться для двумерной случайной величины, для которой дана таблица распределения

Основные числовые характеристики для системы двух случайных величин

Рассмотрим теперь основные числовые характеристики для случайных величин $X$ и $Y$, которые включены в систему двух случайных величин $(X,Y)$.

Среднее квадратического отклонение:

Рассмотрим далее числовые характеристики двумерной случайной величины $(X,Y)$.

Готовые работы на аналогичную тему

. Если $K_\ne 0$, то горят, что между случайными величинами $X$ и $Y$ существует корреляционная связь. Если же $K_=0$, то говорят, что связь между величинами $X$ и $Y$ отсутствует.

. Отметим, что $\left|r_\right|\le 1$.

Пример задачи на нахождение числовых характеристик двумерной случайной величины

Случайная величина $(X,Y)$ задана следующей таблицей:

Найти коэффициент $a$, математическое ожидание, дисперсию и среднее квадратическое отклонение для случайных величин $X$ и $Y$, а также корреляционный момент и коэффициент корреляции.

Решение: Для нахождения коэффициента $a$ используем условие нормированности для двумерной случайной величины

Следовательно: $5a=1,\ a=0,2$.

Получаем следующую таблицу распределения:

Для удобства дальнейших вычислений найдем сначала $p_=\sum\limits^n_>\ и\ $$p_=\sum\limits^m_>$. Получим:

Получим расширенную таблицу распределения случайной величины:

\[M\left(X\right)=\sum\limits^3__>=7,2\cdot 0,4+10\cdot 0,3+12,8\cdot 0,3=9,72\] \[M\left(Y\right)=\sum\limits^3__>=0,8\cdot 0,29+1,6\cdot 0,47+2,4\cdot 0,24=1,56\]

Пусть дана система двух дискретных случайных величин , возможные значения СВ , СВ , соответствующее вероятности .

Тогда математические ожидания и дисперсии составляющих случайных величин

Если система двух непрерывных случайных величин задана плотностью вероятностей , то

Для описания системы двух случайных величин кроме математических ожиданий и дисперсий составляющих используют и другие характеристики; к их числу относятся корреляционный момент (ковариация) и коэффициент корреляции.

Корреляционным моментом случайных величин X и Y называют математическое ожидание произведения отклонений этих величин

Для вычисления корреляционного момента дискретных величин используют формулу

для непрерывных величин – формулу

Коэффициентом корреляции величин X и Y называют отношение корреляционного момента к произведению средних квадратических отклонений этих величин:

Две случайные величины называются независимыми, если закон распределения одной из них не зависит от того, какие возможные значения приняла другая величина.

Для независимых случайных величин выполняются следующие свойства:

Корреляционный момент и коэффициент корреляции служат для характеристики связи между величинами X и Y.

Если X и Y независимы, то корреляционный момент равен нулю. Обратное не всегда верно: если , то не всегда X и Y независимые случайные величины.

Коэффициент корреляции служит для оценки тесноты линейной связи между X и Y. Если между случайными величинами существует строгая функциональная линейная зависимость: , то при и при , причем, чем ближе абсолютная величина к единице, тем линейная связь сильнее. Если , это означает только отсутствие линейной связи между случайными величинами; любой другой вид связи может при этом присутствовать.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Пример 13.2.53. Матрица распределения системы двух дискретных случайных величин задана таблицей

Найти числовые характеристики системы .

ПРИМЕР 13.2.54. Пусть область D возможных значений двумерной случайной величины – треугольник с границами .Плотность распределения имеет вид . Найдем числовые характеристики системы.

что показывает, что между случайными величинами X и Y существует отрицательная линейная зависимость, то есть при увеличении одной из них другая имеет некоторую тенденцию уменьшаться.

Примеры и задачи для самостоятельного решения

Решить задачи, используя формулы расчета числовых характеристик системы двух случайных величин

3.2.12.1. Закон распределения двумерной случайной величины:

а) Определить закон распределения случайной компоненты X. Найти M(X) и D(X).

б) Проделать то же самое для случайной компоненты Y.

в) Найти коэффициент корреляции.

3.2.12.2. Бросаются две неразличимые игральные кости. Пусть X — сумма выпавших очков, а Y — разность между большим и меньшим числом очков на костях.

а) Построить двумерный ряд распределения.

б) Определить математическое ожидание и дисперсию компонент.

в) Найти коэффициент корреляции системы (X,Y).

X\Y	2	3	4	5	6	7	8	9	10	11	12
0	1/36	0	1/36	0	1/36	0	1/36	0	1/36	0	1/36
1	0	2/36	0	2/36	0	2/36	0	2/36	0	2/36	0
2	0	0	2/36	0	2/36	0	2/36	0	2/36	0	0
3	0	0	0	2/36	0	2/36	0	2/36	0	0	0
4	0	0	0	0	2/36	0	2/36	0	0	0	0
5	0	0	0	0	0	2/36	0	0	0	0	0

3.2.12.3. Решить предыдущую задачу в предположении, что кости помеченные, а СВ Y — разность очков на костях.

X\Y	2	3	4	5	6	7	8	9	10	11	12
-5	0	0	0	0	0	1/36	0	0	0	0	0
-4	0	0	0	0	1/36	0	1/36	0	0	0	0
-3	0	0	0	1/36	0	1/36	0	1/36	0	0	0
-2	0	0	1/36	0	1/36	0	1/36	0	1/36	0	0
-1	0	1/36	0	1/36	0	1/36	0	1/36	0	1/36	0
0	1/36	0	1/36	0	1/36	0	1/36	0	1/36	0	1/36
1	0	1/36	0	1/36	0	1/36	0	1/36	0	1/36	0
2	0	0	1/36	0	1/36	0	1/36	0	1/36	0	0
3	0	0	0	1/36	0	1/36	0	1/36	0	0	0
4	0	0	0	0	1/36	0	1/36	0	0	0	0
5	0	0	0	0	0	1/36	0	0	0	0	0

3.2.12.4. Непрерывная двумерная случайная величина (X,Y) распределена равномерно внутри прямоугольника с центром симметрии в начале координат и сторонами 2a и 2b, параллельными координатным осям.

Найти: а) двумерную плотность вероятности системы; б) плотности распределения составляющих; в) показать, что СВ X и Y независимы и .

3.2.12.5. Двумерная случайная величина (X,Y) задана плотностью распределения

а) Найти плотности распределения составляющих и показать, что X и Y зависимые.

б) Найти корреляционный момент .

Указание. Воспользоваться свойством определенного интеграла: если подынтегральная функция нечетна и пределы интегрирования симметричны относительно начала координат, то определенный интеграл равен нулю.

3.2.12.6. Задана плотность совместного распределения непрерывной двумерной случайной величины (X,Y): в квадрате ; вне квадрата . Найти математические ожидания и дисперсии составляющих.

3.2.12.7. Плотность распределения двумерной непрерывной случайной величины
где D — треугольная область плоскости, координаты точек которых положительны, но лежат ниже прямой . Определить:

а) нормировочный множитель k;

б) математические ожидания и дисперсии составляющих X и Y;

в) коэффициент корреляции между X и Y;

г) вероятность события ;

д) плотность распределения СВ X.

3.2.12.8. Плотность распределения двумерной непрерывной случайной величины

а) нормировочный множитель k;

б) математические ожидания и дисперсии X и Y;

в) коэффициент корреляции между X и Y;

д) функцию распределения случайной величины Y.

3.2.12.9. Независимые случайные величины и имеют математические ожидания и и дисперсии соответственно. Рассмотрим новые случайные величины и . Найти коэффициент корреляции между случайными величинами и .

Читайте также: