Важнейшая теорема геометрии доклад
Обновлено: 08.07.2024
Познакомиться с различными доказательствами теоремы Пифагора.
Понять, что геометрия – это просто.
Автор : Сайфутдинова Элина ,ученица 9 класса Верхнеиндырчинской основной школы Апастовского муниципального района РТ
Программа изучения этой темы:
Исторический обзор начнем с древнего Китая . Здесь особое внимание привлекает математическая книга Чу-пей. В этом сочинении так говорится о пифагоровом треугольнике со сторонами 3, 4 и 5: "Если прямой угол разложить на составные части, то линия, соединяющая концы его сторон, будет 5, когда основание есть 3, а высота 4". В этой же книге предложен рисунок, который совпадает с одним из чертежей индусской геометрии Басхары. Кантор (крупнейший немецкий историк математики) считает, что равенство 3 2 + 4 2 = 5 2 было известно уже египтянам еще около 2300 г. до н. э., во времена царя Аменемхета I (согласно папирусу 6619 Берлинского музея).
По мнению Кантора "натягиватели веревок", строили прямые углы при помощи прямоугольных треугольников со сторонами 3, 4 и 5.
Несколько больше известно о теореме Пифагора у вавилонян . В одном тексте, относимом ко времени Хаммураби , т. е. к 2000 г. до н. э., приводится приближенное вычисление гипотенузы прямоугольного треугольника. Отсюда можно сделать вывод, что в Двуречье умели производить вычисления с прямоугольными треугольниками, по крайней мере в некоторых случаях. Основываясь, с одной стороны, на сегодняшнем уровне знаний о египетской и вавилонской математике, а с другой-на критическом изучении греческих источников, Ван-дер-Варден (голландский математик) сделал следующий вывод: "Заслугой первых греческих математиков, таких как Фалес, Пифагор и пифагорейцы, является не открытие математики, но ее систематизация и обснование. В их руках вычислительные рецепты, основанные на смутных представлениях, превратились в точную науку" .
Геометрия у индусов , как и у египтян и вавилонян, была тесно связана с культом. Весьма вероятно, что теорема о квадрате гипотенузы была известна в Индии уже около 18 века до н. э. В настоящее время известно, что эта теорема не была открыта Пифагором. Однако одни полагают, что Пифагор первым дал ее полноценное доказательство, а другие отказывают ему и в этой заслуге.
Как мы видим, история математики почти не сохранила достоверных данных о жизни Пифагора и его математической деятельности. Зато легенда сообщает даже ближайшие обстоятельства, сопровождавшие открытие теоремы. Рассказывают, что в честь этого открытия Пифагор принес в жертву 100 быков.
Приведем различные формулировки теоремы Пифагора в переводе с греческого, латинского и немецкого языков.
У Евклида эта теорема гласит (дословный перевод):
"В прямоугольном треугольнике квадрат стороны, натянутой над прямым углом, равен квадратам на сторонах, заключающих прямой угол".
Латинский перевод арабского текста Аннаирици (около 900 г. до н. э.), сделанный Герхардом Клемонским (начало 12 в.), в переводе на русский гласит:
"Во всяком прямоугольном треугольнике квадрат, образованный на стороне, натянутой над прямым углом, равен сумме двух квадратов, образованных на двух сторонах, заключающих прямой угол".
В Geometria Culmonensis (около 1400 г.) в переводе теорема читается так:
"Итак, площадь квадрата, измеренного по длинной стороне, столь же велика, как у двух квадратов, которые измерены по двум сторонам его, примыкающим к прямому углу" .
В первом русском переводе евклидовых "Начал" , сделанном Ф. И. Петрушевским , теорема Пифагора изложена так:
"В прямоугольных треугольниках квадрат из стороны, противолежащей прямому углу, равен сумме квадратов из сторон, содержащих прямой угол" .
Если дан нам треугольник
И притом с прямым углом,
То квадрат гипотенузы
Мы всегда легко найдем:
Катеты в квадрат возводим,
Сумму степеней находим —
И таким простым путем
К результату мы придем.

Доказательство теоремы Пифагора учащиеся средних веков считали очень трудным и называли его Dons asinorum- ослиный мост, или elefuga- бегство “убогих”, так как некоторые “убогие” ученики, не имевшие серьезной математической подготовки, бежали от геометрии. Слабые ученики, заучившие теоремы наизусть, без понимания, и прозваны по этому “ослами”, были не в состоянии преодолеть теорему Пифагора, служившую для них вроде непреодолимого моста.
Простейшее доказательство теоремы получается в простейшем случае равнобедренного прямоугольного треугольника. Вероятно, с него и начиналась теорема. В самом деле, достаточно просто посмотреть на мозаику равнобедренных прямоугольных треугольников (рис. 1), чтобы убедиться в справедливости теоремы. Например, для ABC: квадрат, построенный на гипотенузе АС, содержит 4 исходных треугольника, а квадраты, построенные на катетах,— по два. Теорема доказана.

Дано: ABC -прямоугольный треугольник, С = 90º.
Доказать: AB 2 =AC 2 +BC 2
1) Проведем высоту CD из вершины прямого угла С .
2) По определению косинуса угла соsА = AD/AC=AC/AB , отсюда следует
3) Аналогично соsВ = BD/BC=BC/AB , значит
4) Сложив полученные равенства почленно, получим:
AC 2 +BC 2 =АВ*(AD + DB)
Дано: ABC -прямоугольный треугольник

Доказать: S ABDE =S ACFG +S BCHI
Пусть ABDE -квадрат, построенный на гипотенузе прямоугольного треугольника ABC , а ACFG и BCHI -квадраты, построенные на его катетах. Опустим из вершины C прямого угла перпендикуляр CP на гипотенузу и продолжим его до пересечения со стороной DE квадрата ABDE в точке Q ; соединим точки C и E , B и G . Очевидно, что углы CAE=GAB(=A+90°) ; отсюда следует, что треугольники ACE и AGB (закрашенные на рисунке) равны между собой (по двум сторонам и углу, заключённому между ними). Сравним далее треугольник ACE и прямоугольник PQEA ; они имеют общее основание AE и высоту AP , опущенную на это основание, следовательно
Точно так же квадрат FCAG и треугольник BAG имеют общее основание GA и высоту AC ; значит,
Отсюда и из равенства треугольников ACE и GBA вытекает равновеликость прямоугольника QPBD и квадрата CFGA ; аналогично доказывается и равновеликость прямоугольника QPAE и квадрата CHIB . А отсюда, следует, что квадрат ABDE равновелик сумме квадратов ACFG и BCHI , т.е. теорема Пифагора.
Приведем еще одно доказательство, которое имеет вычислительный характер, однако сильно отличается от всех предыдущих. Оно опубликовано англичанином Хоукинсом в 1909 году; было ли оно известно до этого - трудно сказать.
Прямоугольный треугольник ABC с прямым углом C повернем на 90° так, чтобы он занял положение A'CB'. Продолжим гипотенузу A'В' за точку A' до пересечения с линией АВ в точке D. Отрезок В'D будет высотой треугольника В'АВ. Рассмотрим теперь заштрихованный четырехугольник A'АВ'В. Его можно разложить на два равнобедренных треугольника САA' и СВВ' (или на два треугольника A'В'А и A'В'В).
Треугольники A'В'А и A'В'В имеют общее основание с и высоты DA и DB, поэтому:
S A'AB'B =c*DA/2+ c*DB/2=c(DA+DB)/2=c²/2
Сравнивая два полученных выражения для площади, получим:

Это доказательство также имеет вычислительный характер. Можно использовать рисунки для доказательства основанного на вычислении площадей двумя способами.
Для того чтобы доказать теорему пользуясь первым рисунком достаточно только выразить площадь трапеции двумя путями.
При равнивая правые части получим:


Доказательство основанное на теории подобия.
В прямоугольном треугольника АВС проведем из вершины прямого угла высоту CD; тогда треугольник разобьется на два треугольника, также являющихся прямоугольными. Полученные треугольники будут подобны друг другу и исходному треугольнику. Это легко доказать, пользуясь первым признаком подобия (по двум углам). В самом деле, сразу видно что, кроме прямого угла, треугольники АВС и ACD имеют общий угол a, треугольники CBD и АВС - общий угол b. То, что малые треугольники также подобны друг другу, следует из того, что каждый из них подобен большому треугольнику. Впрочем, это можно установить и непосредственно.

Доказательство индийского математика Басхары изображено на рисунке. В пояснение к нему он написал только одну строчку: "Смотри!". Ученые считают, что он выражал площадь квадрата ,построенного на гипотенузе, как сумму площадей треугольников (4ab/2) и площадь квадрата (a-b)². Следовательно:

Существует одно интересное приложение обобщения теоремы Пифагора, которое встречается во многих учебниках геометрии под названием теоремы о гиппократовых луночках.

Гиппократ Хиосский (вторая половина пятого века до н. э., Афины) занимался квадратурой луночек. Он называл луночкой часть плоскости, ограниченную двумя дугами окружностей. Наше предложение в том виде, как оно будет здесь сформулировано, не встречается у самого Гипократа, который нашел квадратуру только для некоторых луночек. Во всей общности теорему доказал араб Ибн Альхаитам:
"Если на гипотенузе прямоугольного треугольника как на диаметре описать полуокружность, лежащую с той же стороны гипотенузы, что и сам треугольник, то она пройдет через вершину прямого угла." Эту теорему греки приписывали Фалесу Милетскому, но в действительности ее знали еще древние вавилоняне.
Для того, чтобы доказать теорему о гиппократовых луночках, докажем следующее предложение: Если на катетах и на гипотенузе прямоугольного треугольника построены какие угодно подобные между собой фигуры Fa, Fb, Fc, так, что катеты и гипотенуза являются сходственными отрезками этих фигур, то имеет место равенство: Fa+Fb=Fc.
Для доказательства воспользуемся следующей теоремой из теории подобия: площади подобных многоугольников относятся как квадраты сходственных сторон .
Если через Fa, Fb, Fc обозначить площади подобных многоугольников, построенных на катетах a, b и гипотенузе с прямоугольного треугольника, то согласно вспомогательной теореме можно написать:
Эта пропорция означает,что можно найти число k (коэффицент пропорциональности) такое, что
Умножив обе части равенства на k и принимая во внимание предыдущие равенства, получим:
Если равенство Fa+Fb=Fc имеет место хотя бы для одной тройки подобных между собой многоугольников, построенных на катетах и на гипотенузе прямоугольного треугольника АВС так, что АС, ВС и АВ есть сходственные отрезки этих многоугольников, то
(где k имеет какое-то определенное значение, зависящее от выбора многоугольников, - нам совершенно не важно, какое именно). Но отсюда вытекает, что
а это влечет за собой тот факт,что равенство Fa+Fb=Fc выполняется для любых построенных на сторонах прямоугольного треугольника подобных многоугольников, в частности, и для квадратов.
Пусть АВС - прямоугольный треугольник с прямым углом при вершине С, построенный на векторах. Тогда справедливо векторное равенство: b+c=a
возводя обе части в квадрат, получим
Так как a перпендикулярно b, то ab=0, откуда
Нами снова доказана теорема Пифагора.
Если треугольник АВС - произвольный, то та же формула дает т. н. теорему косинусов , обобщающую теорему Пифагора.
На этой диаграмме показано на сколько больше доказательств стало в наше время


Из-за чертежей, сопровождающих теорему Пифагора, учащиеся называли ее также "ветряной мельницей", составляли стихи вроде "Пифагоровы штаны на все стороны равны", рисовали карикатуры.
Теорема Пифагора замечательна и тем, что сама по себе она вовсе не очевидна. Например, свойства равнобедренного треугольника можно видеть непосредственно на чертеже. Но сколько ни смотри на прямоугольный треугольник, никак не увидишь, что между его сторонами есть простое соотношение: c 2 =a 2 +b 2 .
Вывод. Теорема Пифагора - одна из главных и, можно сказать, самая главная теорема геометрии. Значение ее состоит в том, что из нее или с ее помощью можно вывести большинство теорем геометрии.
Рассмотрев различные типы доказательств теоремы Пифагора, я убедилась в её совершенстве, увидев её красоту, простоту и значимость.
Похожие документы:
Книга посвящена одной из самых интересных и вместе с тем дискуссионных проблем раннегреческой культуры пифагорейскому вопросу. На основе анализа античных источников автор знакомит читателя с жизнью и деятельностью Пифагора,
Книга посвящена одной из самых интересных и вместе с тем дискуссионных проблем раннегреческой культуры - пифагорейскому вопросу. На основе анализа античных источников автор знакомит читателя с жизнью и деятельностью Пифагора,
Теория и история
Людвиг фон МизесТЕОРИЯ И ИСТОРИЯИнтерпретация социально-экономической эволюцииПеревод с английского под ред.доктора экономических наук, профессора А.Г.
Цикл задуман автором как своеобразная библиотечка философской литературы по широкому кругу проблем. Он рассчитан на читателя, которому интересно философствование само по себе.
Из города Ткварчели, которая научила меня работать, когда я работаю, Аркадию Иосифовичу Слуцкому из города Краснодара, который научил меня думать, когда я думаю
Эта книга посвящается Константину Константиновичу Минджия с улицы Инге, который научил меня учиться, когда я учусь, Русудан Григорьевне Гогия из города Ткварчели, которая научила меня работать, когда я работаю, Аркадию Иосифовичу
Теория Всего Глава Тени Глава решение
Предлагаемая Вашему вниманию книга известного специалиста по квантовым компьютерам и квантовым вычислениям Дэвида Дойча своим выходом во многом обязана поддержке ректора Московского Государственного университета академика РАН В.
- Для учеников 1-11 классов и дошкольников
- Бесплатные сертификаты учителям и участникам
Автор: Попов Е.
Учитель: Попова Г.А .
2) Биография Пифагора………………………………………..…стр.4-7
4) История теоремы Пифагора…………………………….…….стр.10-12
5) Формулировки теоремы………………………………….…. стр.13
6) Различные способы доказательства теоремы Пифагора
А) Простейшее доказательство……………………………………….……… стр.14
Б) Не алгебраические доказательства теоремы …………………………. стр.14-17
6) Задачи на применение теоремы Пифагора……………….…стр.21-24
8) Источники информации, используемая литература………стр.26
Я решил провести исследования по геометрии. Меня заинтересовали вопросы, связанные с Пифагором и его знаменитой теоремой. Теорема Пифагора важнейшая теорема геометрии . На уроках мы рассматривали доказательство теоремы Пифагора, говорили о самом Пифагоре, но в школьной программе этой теме уделяется мало времени, и мне захотелось узнать ответы на свои вопросы: Кто же на самом деле открыл теорему Пифагора? Сколько существует доказательств теоремы? Почему она долгое время называлась "теоремой невесты"? и т.д.
Ответы на свои вопросы я искал в Интернете, в книгах, журналах.
Цель работы: Расширение знаний по исследуемой теме. Применение полученных знаний к решению новых познавательных задач. Формирование информационной компетентности.
В работе я кратко рассказываю о личности великого философа, о его жизни и о школе, которую основал Пифагор. Далее речь идёт об истории теоремы, формулировках и различных доказательствах. Я рассматриваю доказательства теоремы, приведённые знаменитыми учёными-математиками прошлого: Евклидом, Хоукинсом, Вальдхеймом, Басхарой, Гиппократом, Эпштейном, Перигалем и другими. Все эти доказательства чрезвычайно интересны и важны. В своей работе я привожу около 20 способов доказательства этой теоремы с целью нахождения путей применения полученных мною знаний для решения различных геометрических задач
Работа в Интернете, с дополнительными источниками позволила найти самый различный материал по данной теме.
БИОГРАФИЯ ПИФАГОРА
ПИФАГОР САМОССКИЙ
(ок. 580 – ок. 500 г. до н.э.)
Пифагор Самосский (рис.1) жил около 2,5 тысяч лет тому назад. Дошедшие до нас биографические сведения о Пифагоре отрывочны и далеко не достоверны. О жизни Пифагора известно немного. Он родился в 576 г. до н.э. в Древней Греции на острове Самос (рис.2), который находится в Эгейском море у берегов Малой Азии, поэтому его называют Пифагором Самосским.

Отцом Пифагора был рез-чик по драгоценным камням. Имя матери Пифагора не-известно. По многим антич-ным свидетельствам, родив-шийся мальчик был сказочно красив, а вскоре проявил и свои незаурядные способно-сти . Среди учителей юного Пифагора традиция называет имена старца Гермодаманта и Ферекида Сиросского (хотя и нет твердой уверенности в том, что именно Гермодамант
и Ферекид были первыми учителями Пифагора). Целые дни проводил юный Пифагор у ног старца Гермодаманта, внимая мелодии кифары и гекзаметрам Гомера.
Страсть к музыке и поэзии великого Гомера Пифагор сохранил на всю жизнь. И, будучи признанным мудрецом, окруженным толпой учеников, Пифагор начинал день с пения одной из песен Гомера. Ферекид же был философом и считался основателем италийской школы философии. Таким образом, если Гермодамант ввел юного Пифагора в круг муз, то Ферекид обратил его ум к логосу. Ферекид направил взор Пифагора к природе и в ней одной советовал видеть своего первого и главного учителя.
В 548 г. до н.э. Пифагор прибыл в Навкратис - самосскую колонию, где было у кого найти кров и пищу. Изучив язык и религию египтян, он уезжает в Мемфис. Несмотря на рекомендательное письмо фараона, хитроумные жрецы не спешили раскрывать Пифагору свои тайны, предлагая ему сложные испытания. Но влекомый жаждой к знаниям, Пифагор преодолел их все, хотя по данным раскопок египетские жрецы не многому могли его научить, т.к. в то время египетская геометрия была чисто прикладной наукой (удовлетворявшей потребность того времени в счете и в измерении земельных участков). Поэтому, научившись всему, что дали ему жрецы, он, убежав от них, двинулся на родину в Элладу. Однако, проделав часть пути, Пифагор решается на сухопутное путешествие, во время которого его захватил в плен Камбиз, царь Вавилона, направлявшийся домой. Вавилоняне ценили умных людей, поэтому он нашёл своё место среди вавилонских мудрецов. Пифагору было, чему поучится. Наука Вавилона была более развитой, нежели египетская. Наиболее поразительными были успехи алгебры. Вавилоняне изобрели и применяли при счёте позиционную систему счисления, умели решать линейные, квадратные и некоторые виды кубических уравнений.
Пифагор прожил в Вавилоне около десяти лет и в сорокалетнем возрасте вернулся на родину. Но на острове Самос он оставался недолго. В знак протеста против тирана Поликрата, который тогда правил островом, поселился в одной из греческих колоний Южной Италии в городе Кротоне.
Там Пифагор организовал тайный союз молодёжи из представителей аристократии. В этот союз принимались с большими церемониями после долгих испытаний. Каждый вступающий отрекался от своего имущества и давал клятву хранить в тайне учения основателя. Пифагорейцы, как их позднее стали называть, занимались математикой, философией, естественными науками. В школе (рис.3,4) существовал декрет, по которому авторство всех математических работ приписывалось учителю.
Пифагор–это не имя, а прозвище, данное ему за то, что он высказывал истину также постоянно, как дельфийский аракул (“Пифагор” значит “убеждающий речью”.) В результате первой же прочитанной лекции Пифагор приобрёл 2000 учеников .
Пифагорова школа
Р ис.4
Рис .5 Рафаэль.1510-1511 г
Пифагорейцами было сделано много важных открытий в арифметике и геометрии, в том числе:
теорема о сумме внутренних углов треугольника;
построение правильных многоугольников и деление плоскости на некоторые из них;
геометрические способы решения квадратных уравнений;
деление чисел на чётные и нечётные, простые и составные; введение фигурных, совершенных и дружественных чисел;
доказательство того, что не является рациональным числом;
создание математической теории музыки и учения об арифметических, геометрических и гармонических пропорциях и многое другое.
Обучение в школе Пифагора было двухступенчатым. Одни ученики назывались математиками, т.е. познавателями науки, а другие – акусматиками, т.е. слушателями.
Пифагорейская система знаний состояла из четырёх разделов:
1. Арифметика (учение о числах).
2. Геометрия (учение о фигурах и их измерениях).
3. Музыка (учение о гармонии и теории музыки).
4. Астрономия (учение о строении Вселенной)
В пифагорейской школе много внимания уделялось музыке, живописи (рис. 5 Пифагор в окружении учеников. Афинская школа 1510-1511 ). физическому развитию, здоровью. Известно, что Пифагор четыре раза был Олимпийским чемпионом. Этого крепкого юношу с упрямой шеей и коротким носом, настоящего драчуна судьи одной из первых в истории Олимпиады не хотели допускать к соревнованиям по кулачному бою, укоряя его маленьким ростом. Он пробился и победил всех противников. Пифагор не только сам участвовал в Олимпиадах, но и воспитал целую плеяду великих олимпийцев.
Союз пифагорейцев был тайным. Эмблемой или опознавательным знаком союза являлась пентаграмма (рис.6)–пятиконечная звезда. Пентаграмме присваивалась способность защищать человека от злых духов .
У немецкого поэта Гёте в трагедии "Фауст", описывается
случай, когда дьявол Мефистофель проник в жилище
учёного Фауста, потому что пентаграмма на его доме была плохо начерчена, и промежуток в уголке остался.
Мефистофель : Нет, трудновато выйти мне теперь, тут кое-что мешает мне немного: Волшебный знак у вашего порога.
Фауст: Не пентаграмма ль этому виной? Но как же, бес, пробрался ты за мной? Каким путем впросак попался?
Мефистофель: Изволили ее вы плохо начертить, и промежуток в уголку остался. Там, у дверей, и я свободно мог вскочить
Этот пятиугольник обладает интересным геометрическим свойством: поворотной симметрией пятого порядка. То есть имеет пять осей симметрии, которые совмещаются при каждом повороте на 72º.. Именно этот тип симметрии наиболее распространён в живой природе у цветков незабудки, гвоздики, колокольчика, шиповника, лапчатки гусиной, вишни (рис. 7), груши, яблони, малины, рябины и т.д. Поворотная симметрия пятого порядка встречается и в животном мире, например, у морской звезды (рис. 8) и панциря морского ежа.

. Прошло 20 лет. Около сорока лет учёный посвятил созданной им школе. Слава о братстве разнеслась по всему миру. Однажды к Пифагору приходит Килон, человек богатый, но злой, желая спьяну вступить в братство. Получив отказ, Килон начинает борьбу с Пифагором, воспользовавшись поджогом его дома. При пожаре пифагорейцы спасли жизнь своему учителю ценой своей, после чего Пифагор затосковал и вскоре, по одной из версий, покончил жизнь самоубийством, по другой из версий, в возрасте восьмидесяти лет Пифагор был убит в уличной схватке во время народного восстания . После его смерти ученики окружили имя своего учителя множеством легенд.
ЛЕГЕНДЫ, СВЯЗАННЫЕ С ИМЕНЕМ ПИФАГОРА
По одной из легенд отцом Пифагора был сириец Мнесарх. Однажды по торговым делам он прибыл из своего родного Тира на остров Самос. Год был неурожайным, население голодало, и Мнесарх устроил бесплатную раздачу хлеба народу. В благодарность его удостоили самосского гражданства.
По словам историка Апулея "Мнесарх славился среди мастеров своим искусством вырезать геммы, но стяжал скорее славу, чем богатство". Сохранилось предание, согласно которому Мнесарх вместе со своим учеником вырезал перстень дивной красоты. Этот перстень перешёл к правителю острова Самос Поликрату и ценился им превыше всего на свете.
Однажды египетский фараон Амасис, состоящий с самосским тираном в дружеских отношениях, встревожился его великим преуспеванием и написал Поликрату письмо, в котором говорил так: "приятно узнать, что друг мой счастлив. Но всё те твои успехи не радуют меня, так я знаю, сколь ревниво божество к человеческому счастью. Поэтому я желал бы, чтобы и у меня самого, и моих друзей одно удавалось, а другое – нет, чтобы лучше на своём веку мне непременно сопутствовали успехи и неудачи, чем быть счастливому всегда. Ведь мне не приходилось слышать ещё ни об одном человеке, кому бы всё удавалось, а в конце концов он не кончил плохо. Поэтому послушайся моего совета теперь и ради своего счастья поступи так: обдумай, что тебе дороже всего на свете и потеря чего может больше всего огорчить тебя. Эту вещь ты закинь так, чтобы она не попадалась никому в руки. И если и тогда успехи у тебя не будут сменяться неудачами, то и впредь применяй то же средство по моему совету". Поликрат нашёл совет Амасиса мудрым. "Посадив людей на корабль, он сам поднялся на борт и приказал затем выйти в море. Когда корабль отошёл далеко от острова, Поликрат снял перстень и на глазах у всех своих спутников бросил в море. После этого, опечаленный потерей, он вернулся во дворец.
А спустя пять или шесть дней какой-то рыбак поймал большую красивую рыбу и решил, что это достойный подарок Поликрату. Он принёс рыбу во дворец, а слуги, выпотрошив её, нашли в брюхе тот Поликратов перстень. Поликрат понял тогда, что это божественное знамение, и написал Амасису обо всём. Амасис же, прочтя послание Поликрата, убедился, что ни один человек не может уберечь другого от предречённой ему участи и что Поликрат не кончит добром, так как он преуспевает во всём и даже находит то, что забросил".
Пророчество Амасиса сбылось. Опасаясь владычества Поликрата на море, персы хитростью выманили Поликрата из Самоса, и зверски убили его.
Легенда о Поликратовом перстне, в котором нашла отражение вечная тема непостоянства земного счастья, стала популярным литературным сюжетом. Вспомним "Поликратов перстень" Шиллера:
На кровле он стоял высоко
И на Самос богатый око
С весельем гордым преклонял.
"Сколь щедро взыскан я богами!
Сколь счастлив я между царями!"
Царю Египта он сказал.
Имя матери Пифагора не сохранилось. Некоторые называли её Пифаидой, дочерью рода Анкея – основателя Самоса. Другие утверждали, будто бы сам Мнесарх назвал жену Пифаидой, а сына – Пифагором в честь дельфийской прорицательницы Пифии. Сделал же так Мнесарх после того, как получил от Дельфийского оракула весть о том, что жена подарит ему необыкновенного сына. Наконец, многие, имея на то основания, считали, что Пифагор – это не имя, а прозвище. Поскольку мудрый учитель высказывал истину столь же постоянно и авторитетно, как и дельфийская Пифия, он был прозван Пифагором.
Слово Пифагор можно перевести как вещающий (прорицающий) как Пифия. Версия о том, что Пифагор это имя не собственное, а прозвище, представляется наиболее правдоподобной. Ведь и знаменитый философ Аристокл известен нам не по своему настоящему имени, а по прозвищу, которое он получил за свою мускулатуру гимнаста, – широкий, широкоплечий, по-гречески Платон.

В процессе работы над индивидуальным проектом по математике "Теорема Пифагора" учеником 9 класса гимназии была поставлена и реализована цель рассмотреть практическое применения теоремы Пифагора в разных сферах деятельности человека и областях науки, помимо математики.
Подробнее о проекте:
В ученической исследовательской работе по математике "Теорема Пифагора" автор проводит анализ учебно-методической литературы и находит интересные сведения о Пифагоре. Также в проекте представлена правильная формулировка Теоремы Пифагора, приведено доказательство теоремы и представлены знаменитые философские высказывания Пифагора.
В готовом творческом и исследовательском проекте по математике "Теорема Пифагора" учащимся дано доказательство теоремы Пифагора через подобные треугольники, а также рассмотрено применение теоремы Пифагора в строительстве, в мобильной связи, в астрономии и в литературе. Школьник рассуждает над актуальностью применения теоремы Пифагора в повседневной жизни человека.
Оглавление
Введение
1. Это интересно знать.
2. Формулировка теоремы Пифагора.
3. Доказательство теоремы.
4. Философские высказывания Пифагора.
5. Доказательство теоремы Пифагора через подобные треугольники.
6. Применение теоремы Пифагора. Строительство.
7. Мобильная связь.
8. Астрономия.
9. Литература.
10. Применение теоремы Пифагора.
Выводы и заключение
Список литературы
Введение
На уроках геометрии мы познакомились с одной из важнейших теорем геометрии для прямоугольного треугольника, известной с древних времен – теоремой Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. Кратко познакомились с историей этой теоремы, рассмотрели одно из ее доказательств, также узнали, что существуют и другие способы доказательства.
Причина такой популярности теоремы Пифагора очевидна: простота, красота и широкая значимость. Однако теорема Пифагора проста, но не так очевидна. Это сочетание двух противоречивых начал и придает ей особую притягательную силу, делает ее красивой. Кроме этого, теорема Пифагора имеет огромное значение: она применяется в геометрии буквально на каждом шагу, и тот факт, что существует около 500 различных доказательств этой теоремы (геометрических, алгебраических, механических и т.д.) свидетельствует о гигантском числе ее конкретных реализаций. Зная теорему Пифагора, можно находить ее новые применения и способы доказательств.
С одной стороны – теорема Пифагора изучается и доказывается в школьном курсе геометрии, а с другой стороны - школьного материала явно недостаточно для того, чтобы показать ее практическую значимость в различных, в том числе и современных сферах деятельности человека.
Цель работы: Изучение практического применения теоремы Пифагора.
- Изучение биографии Пифагора.
- Изучение истории появления и развития теоремы Пифагора.
- Рассмотрение доказательства теоремы Пифагора.
- Подобрать интересные задачи, решаемые с помощью теоремы Пифагора.
Основные методы исследования: Метод исследования, систематизации и обработки данных.
Гипотеза: если теорема Пифагора так популярна и сегодня, то в ней заложены такие основы, которые позволяют использовать ее в различных, в том числе и современных сферах деятельности человека.
Объект исследования: практическое применение теоремы Пифагора в современной деятельности человека.
Предмет исследования: теорема Пифагора.
Это интересно знать
В течение 22 лет он проходил обучение в храмах Мемфиса и получил посвящение высшей степени. Здесь же он глубоко изучил математику, науку чисел или всемирных принципов, из которой впоследствии сделал центр своей системы. Кроме того, что Пифагор был математиком, он также имел отношение к литературе и философии.
Пифагора можно отнести и к великим мыслителям своего времени. Одна из самых главных заслуг Пифагора-это доказательство теоремы, которая носит его имя. Существует около 500 способов её доказательства, и это одна из теорем, которая доказывает большую часть математических теорем.
Формулировка теоремы Пифагора
Теорема Пифагора — одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника:
Сумма квадратов длин катетов равна квадрату длины гипотенузы.a²+b²=c²
Нужно знать зависимость между катетами и гипотенузой в прямоугольном треугольнике. Эту зависимость подметили еще в глубокой древности и доказали теорему, которую знают теперь почти все школьники. Эта теорема носит имя Пифагора.
Квадраты, построенные на катетах, состоят из 2-х одинаковых треугольников. А квадрат, построенный на гипотенузе, состоит из 4-х таких треугольников. Вероятно, факт, изложенный в теореме Пифагора, сначала был дан для равнобедренных треугольников. Таким образом, площадь квадрата построенного на стороне С, равна сумме площадей квадратов, построенных на сторонах А и В.
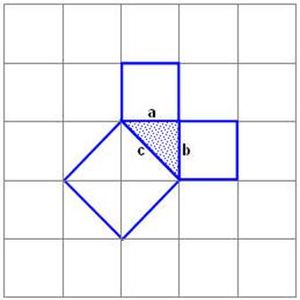
Доказательство теоремы
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. И в этом случае так же площадь квадрата построенного на гипотенузе С, будет равна сумме площадей квадратов, построенных на сторонах А и В.
Задача
Древние египтяне для построения прямоугольных треугольников пользовались веревкой с завязанными на ней на одинаковых расстояниях узелками. По одной стороне они откладывали 3 отрезка, на другой 4, а на третьей 5. Правильно ли они поступали?
Треугольник со сторонами 3, 4, 5 теперь мы называем египетским.
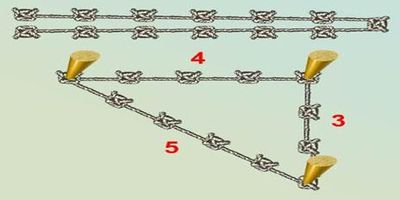
Философские высказывания Пифагора
- Делай лишь то, что впоследствии не огорчит тебя и не заставит раскаиваться.
- Статуя формой своей хороша, а человека украсят дела.
- Будь с тем, кто ношу взваливает, не будь с тем, кто ношу сваливает.
Доказательство теоремы Пифагора через подобные треугольники
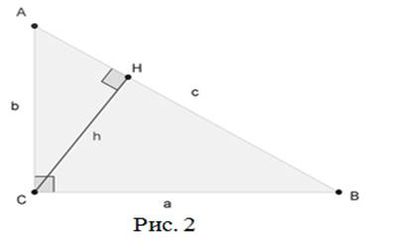
Проведём высоту из вершины C на гипотенузу AB, основание высоты обозначим как H.
Прямоугольный треугольник ACH подобен треугольнику ABC по двум углам (∠ACB=∠CHA=90%, ∠A- общий). Аналогично, треугольник CBH подобен ABC.
из подобия треугольников получаем, что
Отсюда имеем, что
Сложив полученные равенства, получаем
Что и требовалось доказать.
Применение теоремы Пифагора. Строительство
Задача 1
От столба высотой 9 м к дому натянут провод, который крепится на высоте
3 м от земли (см. рисунок). Расстояние от дома до столба 8 м. Вычислите длину провода.

Решение задачи

Изобразим рисунок схематично. Проведем отрезок СЕ, параллельный AD. AECD - прямоугольник, т.к. все углы прямые. Следовательно, СЕ=AD.
По теореме Пифагора
Задача 2
Длина стремянки в сложенном виде равна 1,85 м, а её высота в разложенном виде составляет 1,48 м. Найдите расстояние (в метрах) между основаниями стремянки в разложенном виде.
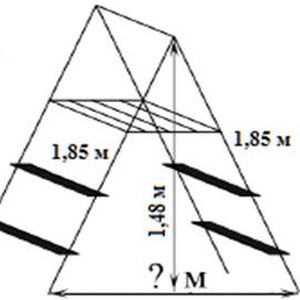
Решение задачи
Данная задача сводится к нахождению катета прямоугольного треугольника. Пусть х — искомое расстояние, тогда:
Задача 3
Девочка прошла от дома по направлению на запад 880 м. Затем повернула на север и прошла 900 м. После этого она повернула на восток и прошла ещё 400 м. На каком расстоянии (в метрах) от дома оказалась девочка?
Решение задачи
Восток и запад — противоположные направления, поэтому девочка прошла 880 − 400 = 480 м на запад. Пусть — гипотенуза прямоугольного треугольника. По теореме Пифагора, гипотенуза ищется следующим образом:
Мобильная связь
Какую наибольшую высоту должна иметь антенна мобильного оператора, чтобы передачу можно было принимать в радиусе R=200 км? (радиус Земли равен 6380 км.)
Решение задачи
Пусть AB=x, BC=R=200 км, OC=r=6380 км.
Используя теорему Пифагора, получим 23 км
Астрономия
Задача 6
На этом рисунке показаны точки A и B и путь светового луча от A к B и обратно. Путь луча показан изогнутой стрелкой для наглядности, на самом деле, световой луч - прямой. Какой путь проходит луч? Поскольку свет идет туда и обратно одинаковый путь, спросим сразу: чему равно расстояние между точками?
Решение задачи
На этом рисунке показан путь светового луча только с другой точки зрения, например из космического корабля. Предположим, что корабль движется влево. Тогда две точки, между которыми движется световой луч, станут двигаться вправо с той же скоростью. Причем, в то время, пока луч пробегает свой путь, исходная точка A смещается, и луч возвращается уже в новую точку C.
Вконце девятнадцатого века высказывались разнообразные предположения о существовании обитателей Марса подобных человеку. В шутку, хотя и не совсем безосновательно, было решено передать обитателям Марса сигнал в виде теоремы Пифагора. Неизвестно, как это сделать; но для всех очевидно, что математический факт, выражаемый теоремой Пифагора, имеет место всюду и поэтому похожие на нас обитатели другого мира должны понять такой сигнал.
Литература
Теорема Пифагора вдохновляла писателей со времен античности и продолжает это делать в наше время. Например, немецкого писателя девятнадцатого века Адельберта фон Шамиссо она вдохновила на написание сонета:
Свет истины рассеется не скоро,
Но, воссияв, рассеется навряд
И, как тысячелетия назад,
Не вызовет сомнения и спора.
Мудрейшие, когда коснется взора
Свет истины, богов благодарят;
И сто быков, заколоты, лежат –
Ответный дар счастливца Пифагора.
С тех пор быки отчаянно ревут:
Навеки всполошило бычье племя
Событие, помянутое тут.
Им кажется: вот-вот настанет время,
И сызнова их в жертву принесут
Какой-нибудь великой теореме…
Если дан нам треугольник И притом с прямым углом, То квадрат гипотенузы Мы всегда легко найдём: Катеты в квадрат возводим, Сумму степеней находим И таким простым путём К результату мы придём.
Применение теоремы Пифагора
Успех развития многих областей науки и техники зависит от развития различных направлений математики. Важным условием повышения эффективности производства является широкое внедрение математических методов в технику и народное хозяйство, что предполагает создание новых, эффективных методов, которые позволяют решать задачи, выдвигаемые практикой. Теорема Пифагора применяется в строительстве, астрономии, мобильной связи, литературе и т.д.
Заключение
В научной литературе зафиксировано 367 доказательств данной теоремы. Вероятно, теорема Пифагора является единственной теоремой со столь внушительным числом доказательств. Такое многообразие можно объяснить лишь фундаментальным значением теоремы для геометрии. Разумеется, концептуально все их можно разбить на малое число классов. Самые известные из них: доказательства методом площадей, аксиоматические и экзотические доказательства (например, с помощью дифференциальных уравнений).
Теорема Пифагора - одна из главных и, можно сказать, самая главная теорема геометрии. Теорема Пифагора триедина: это простота – красота – значимость. Мы познакомились с некоторыми доказательствами теоремы Пифагора.
Есть доказательства, которые рассчитаны на то, что по готовым рисункам, можно воспроизвести доказательство самостоятельно. А это воспитывает познавательный интерес и логическое мышление. До сих пор вызывают интерес древние практические задачи, говорящие об уровне развития прикладной математики в древние века.
1.Прямоугольный треугольник
Прямоугольный треугольник – треугольник , в котором один угол прямой (то есть равен 90˚).
Сторона, противоположная прямому углу, называется гипотенузой прямоугольного треугольника.
Стороны, прилежащие к прямому углу, называются катетами .
Признаки равенства прямоугольных треугольников
Свойства прямоугольного треугольника
1.1. Сумма острых углов прямоугольного треугольника равна 90˚.
1. 2. Катет, противолежащий углу в 30˚, равен половине гипотенузы.
И обратно, если в треугольнике катет вдвое меньше гипотенузы, то напротив него лежит угол в 30˚.
1. 3. Теорема Пифагора : С 2 = A 2 + B 2 , где А, B – катеты, С – гипотенуза.
1. 4. Площадь прямоугольного треугольника с катетами :
1. 5. Высота прямоугольного треугольника, проведенная к гипотенузе выражается через катеты и гипотенузу следующим образом:
1.6. Центр описанной окружности – есть середина гипотенузы.
1. 7. Радиус описанной окружности есть половина гипотенузы :
1. 8. Медиана, проведенная к гипотенузе, равна ее половине
2. Формулировки теоремы Пифагора
Изначально теорема была сформулирована следующим образом:
В прямоугольном треугольнике площадь квадрата, построенного на гипотенузе , равна сумме площадей квадратов, построенных на катетах .
В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
То есть, обозначив длину гипотенузы треугольника через , а длины катетов через и :
Обе формулировки теоремы эквивалентны, но вторая формулировка более элементарна, она не требует понятия площади . То есть второе утверждение можно проверить, ничего не зная о площади и измерив только длины сторон прямоугольного треугольника.
Обратная теорема Пифагора:
Для всякой тройки положительных чисел а,в,с, таких, что а 2 +в 2 =с 2 ,существует прямоугольный треугольник с катетами а,в и гипотенузой с.
3. Различные способы доказательства теоремы Пифагора.
С глубокой древности математики находят все новые и новые доказательства теоремы Пифагора, все новые и новые замыслы ее доказательств. Известно более или менее строгих доказательств около пятисот, но стремление к преумножению их числа сохранилось.
На данный момент в научной литературе зафиксировано 367 доказательств данной теоремы. Такое многообразие можно объяснить лишь фундаментальным значением теоремы для геометрии.
Все их можно разбить на малое число классов. Самые известные из них: доказательства методом площадей, аксиоматические и экзотические доказательства (например, с помощью дифференциальных уравнений).
Приведу некоторые доказательства Теоремы:
Квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на его катетах.
3.1. Простейшее доказательство теоремы получается в случае равнобедренного прямоугольного треугольника. Вероятно, с него и начиналась теорема.
В самом деле, достаточно просто посмотреть на мозаику равнобедренных прямоугольных треугольников, чтобы убедиться в справедливости теоремы. Например, для ΔABC : квадрат, построенный на гипотенузе АС , содержит 4 исходных треугольника, а квадраты, построенные на катетах, - по два. Теорема доказана .
3.2. Метод подобия
Пусть ABC есть прямоугольный треугольник с прямым углом C . Проведём высоту из C и обозначим её основание через H . Треугольник ACH подобен треугольнику ABC по двум углам. Аналогично, треугольник CBH подобен ABC . Введя обозначения ВС=а, АС=в, АВ=с
получаем а/с=|НВ|/а, в/с=|АН|/в
Что эквивалентно а 2 =с*|НВ|; в 2 =с*|АН|
Сложив, получаем а 2 + в 2 =с*(|НВ|+|АН|)=с 2 .
Или а 2 + в 2 =с 2 , что и требовалось доказать
3.3.Доказательства методом площадей
Расположим четыре равных прямоугольных треугольника так, как показано на рисунке.
Четырёхугольник со сторонами c является квадратом, так как сумма двух острых углов 90°, а развёрнутый угол — 180°.
Площадь всей фигуры равна, с одной стороны, площади квадрата со стороной (a+b), а с другой стороны, сумме площадей четырёх треугольников и площади внутреннего квадрата.
(а+в) 2 =4*(ав/2)+с 2 ; а 2 +2ав+в 2 =2ав+с 2 ; или а 2 + в 2 =с 2 , что и требовалось доказать.
3.4.Через определение косинуса угла прямоугольного треугольника
Пусть ΔАВС - данный прямоугольный треугольник с прямым углом С . Проведем высоту CD из вершины прямого угла С .
По определению косинуса угла (Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе) соsА=AD/AC=AC/AB .
Древнекитайское доказательство
3.5. Доказательство Гарфилда
На рисунке три прямоугольных треугольника составляют трапецию. Поэтому площадь этой фигуры можно находить по формуле площади прямоугольной трапеции, либо как сумму площадей трех треугольников.
3.6 . Доказательство Мёльманна
Площадь данного прямоугольника с одной стороны равна 0.5 ab , с другой 0.5 pr , где p – полупериметр треугольника, r – радиус вписанной в него окружности ( r = 0.5(a+b-c)). 0.5ab=0.5pr=0.5(a+b+c)*0.5(a+b-c) Отсюда следует , что с2=а2+b2
3.7. Доказательство Евклида
Идея доказательства Евклида состоит в следующем: попробуем доказать, что половина площади квадрата, построенного на гипотенузе, равна сумме половин площадей квадратов, построенных на катетах, а тогда и площади большого и двух малых квадратов равны.
Попытаемся доказать, что площадь квадрата DECA равна площади прямоугольника AHJK Для этого воспользуемся вспомогательным наблюдением: Площадь треугольника с той же высотой и основанием, что и данный прямоугольник, равна половине площади заданного прямоугольника. Это следствие определения площади треугольника как половины произведения основания на высоту. Из этого наблюдения вытекает, что площадь треугольника ACK равна площади треугольника AHK (не изображённого на рисунке), которая, в свою очередь, равна половине площади прямоугольника AHJK.
Докажем теперь, что площадь треугольника ACK также равна половине площади квадрата DECA. Единственное, что необходимо для этого сделать, — это доказать равенство треугольников ACK и BDA (так как площадь треугольника BDA равна половине площади квадрата по указанному выше свойству). Равенство это очевидно: треугольники равны по двум сторонам и углу между ними. Именно — AB=AK, AD=AC — равенство углов CAK и BAD легко доказать методом движения: повернём треугольник CAK на 90° против часовой стрелки, тогда очевидно, что соответствующие стороны двух рассматриваемых треугольников совпадут (ввиду того, что угол при вершине квадрата — 90°).
Рассуждение о равенстве площадей квадрата BCFG и прямоугольника BHJI совершенно аналогично.
3.8.Доказательство Леонардо да Винчи
Главные элементы доказательства — симметрия и движение.
Пользуясь поворотом на 90 градусов против часовой стрелки вокруг точки A, мы усматриваем равенство заштрихованных фигур CAJI и DABG.
Теперь ясно, что площадь заштрихованной нами фигуры равна сумме половин площадей маленьких квадратов (построенных на катетах) и площади исходного треугольника. С другой стороны, она равна половине площади большого квадрата (построенного на гипотенузе) плюс площадь исходного треугольника. Таким образом, половина суммы площадей маленьких квадратов равна половине площади большого квадрата, а следовательно сумма площадей квадратов, построенных на катетах равна площади квадрата, построенного на гипотенузе.
Применение Теоремы Пифагора.
Теорема Пифагора применяется в строительстве и архитектуре.
При проектировании любых строительных объектов возникает необходимость вычислять стороны прямоугольных треугольников по известным сторонам. Подобные задачи решаются и в нашей повседневной жизни, используя мет оды теоремы Пифагора.
В мобильной связи .
В настоящее время на рынке мобильной связи идет большая конкуренция среди операторов. Чем надежнее связь, чем больше зона покрытия, тем больше потребителей у оператора. При строительстве вышки (антенны) часто приходится решать задачу какую наибольшую высоту должна иметь антенна, чтобы передачу можно было принимать в определенном радиусе. И эти задачи решаются, применив теорему Пифагора.
Мало кто знает, что Пифагор имел отношение не только к математике, но и к литературе. Он и его теорема воспеты в литературе. О ней писали в своих произведениях римский архитектор и инженер Витрувий, греческий писатель-моралист Плутарх, греческий ученый III в. Диоген Лаэрций, математик V в. Прокл и многие другие.
5. Пифагоровы Тройки.
С теоремой Пифагора связана арифметическая задача. Имеются такие тройки натуральных (т. е. целых положительных) чисел x , y , z , что
x 2 + y 2 = z 2 . (1)
Их называют пифагоровыми тройками . Например, годятся числа x=3 , y=4 , z=5 : 9+16=25 . Это пример. А можно ли указать все пифагоровы тройки (x,y,z) ? Иными словами, можно ли найти все решения уравнения x 2 +y 2 =z 2 в натуральных числах? (В связи с терминологией обратите внимание, что решение --- это не одно число, а три.) Да. Ответ таков: каждое такое решение можно представить в виде
x=l(m 2 -n 2 ), y=2lmn, z=l(m 2 +n 2 ), (2)
где l , m , n --- натуральные числа, причем m>n , или в аналогичном виде, в котором x и y меняются местами. Можно чуть короче сказать, что x , y , z из (2) со всевозможными натуральными l и m > n суть все возможные решения (1) с точностью до перестановки x и y . Например, тройка (3,4,5) получается при l=1 , m=2 , n=1 .
То что при любых натуральных l , m , n с m>n тройка (x,y,z) , определяемая согласно (2) , является решением (1) , можно проверить непосредственно путем простого вычисления, и я на этом останавливаться не буду. Интересно другое: почему любое решение обязательно имеет вид (2) ? Об этом я и буду говорить. На самом деле, как это часто бывает, "прокручивая в обратную сторону" мои рассуждения, тоже можно доказать, что любая тройка вида (2) является решением, но на этом я тоже не буду останавливаться. Что при перестановке x и y снова получается решение --- об этом и говорить нечего.
По-видимому, вавилоняне знали этот ответ, но как они к нему пришли --- неизвестно. (Впрочем, не ясно, знали ли они, что все решения (1) представимы в виде (2) , да и задавались ли они таким вопросом. Имеется правдоподобная, хотя и гипотетическая, реконструкция их рассуждений, в которой этим вопросом не задаются, а ищут способ как-нибудь получить побольше решений.) Как его позднее доказывали древние греки --- известно; по существу, их доказательство в модернизированном виде (с явным использованием алгебры) воспроизводится во многих книгах, и, вероятно, многие из вас его знают. А я хочу рассказать несколько более простое доказательство, которое я узнал в свои студенческие годы от моего однокурсника Юры Манина. Ныне Юрий Иванович Манин --- член-корреспондент Российской академии наук, лауреат Ленинской премии, один из директоров международного Математического института им. Макса Планка в Бонне. Ни одного из этих высоких титулов вроде бы не нужно, чтобы придумать то простое рассуждение, которое я сейчас расскажу; в истории неоднократно бывало, что любители придумывали куда более затейливые вещи. Тем не менее, я нигде в литературе не встречал этого рассуждения. Впрочем, не могу поручиться, что его нигде нет или что никто, кроме Манина, такого доказательства не мог придумать. Так что не исключено, что кто-нибудь из вас это рассуждение знает. Но уж точно, что таких среди вас не может быть много --- рассуждение если и является известным, то не общеизвестным.
Сперва несколько простых замечаний, которые предшествуют и обычному доказательству. Если x , y и z имеют общий делитель k>1 , скажем x=ku , y=kv , z=kw , где u , v , w --- натуральные числа, то ясно, что тройка (u,v,w) снова является решением (1) . Обратно, если мы знаем какое-то решение (x,y,z) , то, умножив эти три числа на какое-нибудь натуральное k , мы снова получим решение. Поэтому можно ограничиться разысканием решений, не имеющих общего делителя. В данный момент речь идет об общем делителе всех трех чисел. Но если бы у двух из этих чисел, скажем у x и y , был общий делитель, то тот же делитель был бы и у третьего. Поэтому мы можем ограничиться разысканием решений, в которых любые два числа ( x и y , x и z , y и z ) не имеют общих делителей, больших 1. Это выражают словами: рассматриваемые числа x , y , z попарно взаимно просты.
x=m 2 -n 2 , y=2mn, z=m 2 +n 2 , (3)
где m , n --- натуральные числа и m>n . Заметьте, что я вовсе не утверждаю обратного: что любые (x,y,z) , получающиеся согласно (3) с натуральными m>n , являются решением (1) и попарно взаимно просты. Решением эта тройка будет, но числа x , y , z не обязательно получатся взаимно простыми. Ведь если у m и n есть общий делитель, то он войдет (даже с квадратом) и в x , и в y , и в z .
Так что если бы я хотел настаивать на обратном утверждении, что любые (x,y,z) , получающиеся согласно (3) с натуральными m>n , будут решением (1) с попарно взаимно простыми x , y , z , то я, самое меньшее, должен был бы уточнить: с взаимно простыми m и n . А было бы такого уточнения достаточно? Оказывается, нет (вначале, должен сознаться, я было подумал, что да, но меня поправили). Ведь если m и n оба нечетные, то x получится четным, а y в (3) всегда четное. Но если одно из чисел m , n четное, а другое нечетное, то x получится нечетным, и общим с y у него мог бы быть только нечетный делитель. Тогда у x и y имеется и нечетный простой делитель p . Раз 2mn делится на p , то m или n делится на p , а тогда, раз m 2 -n 2 тоже делится на p , то и второе из чисел m , n делится на p , т. е. m и n не взаимно просты, а мы уже решили, что будем брать только взаимно простые m , n . Но главное, что этого нам сейчас не нужно. Нам надо только установить, что решение (1) с взаимно простыми натуральными x , y , z обязательно представимо в виде (3) с какими-то m , n , а что при каких-то других m , n могут получиться решения с не взаимно простыми x , y , z --- это нас сейчас не касается.
Другое замечание состоит в том, что когда мы ограничиваемся решениями с попарно взаимно простыми x , y , z , то одно из чисел x и y должно быть четным, а другое --- нечетным; z при этом, конечно, нечетно. Действительно, если x и y оба четные, то они не взаимно просты, а имеют общий делитель 2. Если же они оба нечетны, то мы можем написать, что x=2r-1 , y=2s-1 с некоторыми натуральными r , s . Отсюда
z 2 =(2r-1) 2 +(2s-1) 2 =4(r 2 -r+s 2 -s)+2.
Получается, что z 2 делится на 2, но не делится на 4. Но это невозможно: если z нечетно, то z 2 и на 2 не делится, а если z четно, то z 2 делится на 4.
Раз одно из чисел x и y четно, а другое нечетно, то можно считать, что нечетно x , а четно y , --- в противном случае мы просто изменим обозначения. Вот теперь начинается главное. Перепишем (1) так:
y 2 =z 2 -x 2 , 2 - 2 =1
или, обозначая через u и через v , в виде u 2 -v 2 =1 , т. е. (u+v)(u-v)=1 . u и v суть частные двух натуральных чисел, т. е. положительные рациональные числа (дроби). u+v тоже рациональное число, причем положительное. Любое такое число представляется в виде несократимой дроби ; здесь m и n --- натуральные числа, причем взаимно простые (раз дробь несократимая). А если (u-v)=1 , то u-v= . Итак,
m 2 +n 2 где m , n --- взаимно простые натуральные числа. Рассматривая ( как линейную систему уравнений относительно u , v , решим ее, для чего достаточно сложить эти два уравнения, откуда получится 2u , и вычесть второе из первого, откуда получится 2v :
=u=, =v=. (5)
Отсюда видно, кстати, что m>n.
Мы знаем, что и --- несократимые дроби. Если бы мы знали, что дробь тоже несократимая, то из (5) сразу следовали бы соотношения (3). Но пока что мы этого не знаем; однако о дробях , мы знаем, что они несократимые. Поэтому из (5) мы вправе сделать заключение, несколько более слабое, чем (3): существует такое натуральное k, что
m 2 +n 2 =kz, 2mn=ky, m 2 -n 2 =kx. (6)
Допустим, что k имеет нечетный простой делитель p . Тогда 2mn делится на p , а раз это нечетное простое число, то m или n делится на p . Но тогда и одно из слагаемых в левой части равенства m 2 +n 2 =kz , и его правая часть делятся на p ; выходит, что и второе слагаемое в левой части тоже делится на p . Получается, что и m , и n делятся на p , хотя они взаимно просты. Итак, у k нет нечетных простых делителей, так что k есть степень двойки. Вспомним, что y --- четное число, y=2w . Получается, что 2mn=2kw , mn=kw , и если k --- степень двойки (с ненулевым показателем), то число mn четное. Тогда хотя бы одно из чисел m , n --- четное. Но из m 2 +n 2 =kz следует, что m 2 +n 2 --- четное число, и если вдобавок одно из чисел m или n --- четное, то и другое должно быть четным. Снова у m и n нашелся общий делитель. Остается признать, что k=1 , а это и означает (3) .
Читайте также:

