Теория деления многочлена на многочлен доклад 7 класс

Обновлено: 05.07.2024

Различают два вида деления многочлена на многочлен: с остатком и без.

Многочлен $p(x)$ делится на многочлен $s(x)$, если существует такой многочлен $q(x)$, что соблюдается равенство:

Для деления многочлена с остатком существует следующее тождество:

Для любых двух многочленов $p(x)$ и $s(x)$ существует пара многочленов $q(x)$ и $r(x)$, причём такая, что выполняется равенство:

$p(x)=q(x) \cdot s(x) + r(x)$

Ещё одна необходимая теорема:

Остаток от деления многочлена $p(x)$ ненулевой степени на двучлен $x-α$ равен $p(α)$, иными словами, многочлен $p(x)$ при $x= α$ равен $p(α)$.

Деление многочлена на многочлен удобно выполнять в столбик или используя правило Горнера. Ниже мы рассмотрим примеры выполнения деления полиномов в столбик.

Выполним для примера деление многочлена на многочлен и многочлена на двучлен.

Решение:

Для того чтобы разделить многочлен на другой многочлен, нужно его последовательно домножать на какой-либо одночлен до коэффициента и степени при старшем члене делимого многочлена.

Рисунок 1. Деление полинома. Автор24 — интернет-биржа студенческих работ

Например, для этого примера в первом действии $x^2-3x-1$ нужно домножить на $x$ чтобы можно было избавиться от старшего многочлена.

Во втором действии чтобы избавиться от $x^2$, нужно домножить многочлен-делитель на $1$ и полученный многочлен $x^2-3x-1$ вычесть из остатка $x^2+4x-5$, образовавшегося после предыдущего вычитания.

Остаток $7x-4$, полученный на втором этапе, имеет степень, меньшую, чем степень многочлена-делителя, а значит, деление на этом оканчивается. Разложенный многочлен теперь можно записать в виде:

Для выполнения деления многочлена на двучлен также воспользуемся делением столбиком.

Рисунок 2. Деление многочлена на двучлен. Автор24 — интернет-биржа студенческих работ

На первом этапе двучлен-делитель домножим на $2x^4$ чтобы изабиться от старшей степени. Полученное произведение $2x^5-4x^4$ отнимем от делимого многочлена $2x^5-3x^3-x+2$. В остатке имеем $4x^4-3x^3-x+2$.

Теперь для того чтобы избавиться от четвёртой степени, домножаем двучлен на $4x^3$ и отнимаем полученное произведение $4x^4-8x^3$ от остатка с предыдущего действия $4x^4-3x^3-x+2$.

Продолжаем выполнять аналогичные действия до тех пор, пока не получим остаток со степенью переменной меньше чем у двучлена-делителя, здесь он равен $40$.

Презентация на тему: " Деление многочленов Методическая разработка учителя Поляковой Е. А." — Транскрипт:

1 Деление многочленов Методическая разработка учителя Поляковой Е. А.

2 Повторение Выполнить деление: 1). 3 х³ : 3 х² 2). 4 х² : 4 х 3). 6 х³ : 3 х 6). х³ : 3 х 5). 3 х² : 2 х² 4). х³ : 2 х² Выполнить вычитание: 1). 3 х³ 5 х² 6 х 3 х³ + х² 4 х 6 х² 2 х 2). 4 х² х х² 5 х 4 х + 5 3). 6 х³ + 11 х² 1 6 х³ + 9 х² 3 х 2 х² + 3 х 1

3 Многочлены 5 х² 6 х 2; 4 х³ + 2 х² 3 х записаны в стандартном виде, и показатели степеней буквы х расположены в порядке убывания. Тогда первый член многочлена это его старший член; показатель степени буквы х в старшем члене это степень многочлена; член многочлена, не содержащий буквы х это свободный член. 5 х² 6 х 2 это многочлен второй степени; 4 х³ + 2 х² 3 х это многочлен третьей степени.

5 Разделить многочлен 3 х³ 5 х² 6 х + 8 на многочлен 3 х² + х 4. Деление можно выполнить уголком, как и деление натуральных чисел: делимое первый остаток делимое делитель делимое частное делимое остаток 3 х³ 5 х² 6 х х² + х 4 х 3 х³ + х² 4 х 6 х² 2 х 2 6 х² 2 х Остаток равен нулю, поэтому многочлен 3 х³ 5 х² 6 х + 8 делится нацело на многочлен 3 х² + х 4, т. е. в результате деления многочленов снова получился многочлен. + 8

6 Алгоритм деления многочленов уголком 1. Расположить делимое и делитель по убывающим степеням переменной х. 2. Разделить старший член делимого на старший член делителя; полученный одночлен записать первым членом частного. 3. Первый член частного умножить на делитель, результат вычесть из делимого; полученная разность является первым остатком. 4. Старший член этого остатка разделить на старший член делителя; полученный одночлен записать вторым членом частного и умножить его на делитель; результат вычесть из первого остатка; получим второй остаток и т. д. Это следует продолжить до тех пор, пока не будет получен остаток, равный нулю.

7 Как и при делении чисел, результат деления многочленов можно проверить умножением. Если многочлен степени n 1 делится нацело на многочлен степени k 1, k n и в результате получается многочлен степени m 1, m n, то справедливо равенство Это равенство называют формулой деления многочлена на многочлена многочлен называют частным отделения на при этом обязательно, чтобы n = m + k.

8 х² 2 х 35 х 7 х х² 7 х 5 х х Найти частное (результат проверить умножением): 1) (х² 2 х 35) : (х 7);2) ( 4 х² х + 5) : (4 х + 5); 4 х² х х + 5 х 4 х² 5 х 4 х х (х + 5) (х 7) = х² 7 х + 5 х 35 = х² 2 х 35; (4 х + 5) ( х + 1) = 4 х² 5 х + 4 х + 5 = 4 х² х + 5.

9 1. Найти частное (результат проверить умножением): показать 6 х³ + 7 х² 6 х + 13 х 1 2 х² 6 х³ 2 х² 9 х² 6 х + 3 х 9 х² 3 х 3 х х (2 х² + 3 х 1) (3 х 1) =6 х³ 2 х² + 9 х² 3 х 3 х + 1 = = 6 х³ + 7 х² 6 х + 1

10 2. Найти частное (результат проверить умножением): показать 6 х³ + 11 х² 1 2 х² + 3 х 1 3 х 6 х³ + 9 х² 3 х 2 х² + 3 х х² + 3 х 1 0 = 6 х³ + 11 х² 1 (3 х + 1)(2 х² + 3 х 1) = 6 х³ + 9 х² 3 х + 2 х² + 3 х 1 = 11 показать 0 3. Выполнить деление:

12 4. Выяснить, делится ли нацело многочлен Р(х) на многочлен Q(x): 2 х³ + 3 х² 0 показать Ответ: делится, т. к остаток равен нулю.

13 5. Выяснить, при каком значении а многочлен Р(х) делится нацело на многочлен Q(x): Р(х) = 5 х³ 9 х² + 13 х + а,Q(х) = 5 х + 1 Выполним деление уголком: 5 х³ 9 х² + 13 х + а 5 х + 1 х²х² 5 х³ + х² 10 х²+13 х 2 х 10 х² 2 х 15 х + а х + 3 а 3 По смыслу задания остаток а 3 должен равняться нулю, поэтому а 3 = 0, а = 3. Ответ: при а = 3.

14 7 х³ 22 х² + ах 1 х² 3 х х 7 х³ 21 х² + 7 х 7 х² 7 х+ ах х² + 3 х 1 ах 10 х По смыслу задания надо найти те значения а, при которых остаток ах 10 х = (а 10)х должен равняться нулю, поэтому а 10 = 0, а = 10. Ответ: при а = Р(х) = 7 х³ 22 х² + ах 1,Q(х) = х² 3 х + 1

15 7. Найти такой многочлен Q(х), чтобы многочлен Р(х) делился нацело на Q(х) и частное от деления равнялось М(х). 1) Р(х) = 4 х³ 5 х² + 6 х + 9,М(х) = х² 2 х + 3. Решение. По формуле деления должно выполняться равенство Р(х) = М(х) Q(х). Задача свелась к нахождению делителя по известным делимому и частному. Поэтому Q(х) = Р(х) : М(х) 4 х³ 5 х² + 6 х + 9 х² 2 х х 4 х³ 8 х² + 12 х 3 х² 6 х х² 6 х Ответ: Q(х) = 4 х + 3.

16 Деление многочленов с остатком Покажем деление многочленов в случаях, когда многочлены не делятся нацело. Разделить многочлен х³ х² 2 х + 4 на многочлен х² 3 х + 1. Выполним деление уголком: х³ х² 2 х + 4 х² 3 х + 1 х х³ 3 х² + х 2 х² 3 х х² 6 х х + 2 Дальнейшее деление невозможно, так как степень последнего остатка 1 меньше степени делителя 2. Ответ: частное х + 2, остаток 3 х + 2.

17 Формула деления многочлена степени n 1 на многочлен степени k 1, k n с остатком такова: Многочленназывают неполным частным, Деление многочленов с остатком многочлен называют остатком. При этом степень частного m = n k, степень остатка l

18 1. Написать формулу деления многочлена Р(х) на многочлен Q(х): 3) Р(х) = 6 х³ + 3 х² 4 х + 3,Q(х) = 2 х + 1 Решение. Формула деления: Выполним деление Р(х) на Q(х) с остатком: 6 х³ + 3 х² 4 х х + 1 показать 3 х² 6 х³ + 3 х² 4 х х 2 5 Р(х) = (3 х² 2) Q(х) + 5,

19 Решение. Выполним деление Р(х) на Q(х) с остатком R(x) : х³ 3 х² 2 х² + 5 показать 0,5 х х³ + 2,5 х 3 х² 2,5 х 1,5 3 х² 7,5 2,5 х + 7,5 Ответ: частное М(х) = (3 х² 2); остаток R(х) = 2,5 х + 7,5. 2. Найти частное М(х) и остаток R(x) от деления многочлена Р(х) на многочлен Q(х): 2) Р(х) = х³ 3 х²,Q(х) = 2 х² + 5

20 3 Найти такой многочлен Q(х), чтобы при делении многочлена Р(х) на Q(х) частное было равно М(х) и остаток был равен R(x). Решение. По формуле деления должно выполняться равенство Р(х) = М(х) Q(х) + R(x). Задача свелась к нахождению делителя по известным делимому, частному и остатку. Поэтому 2 х³ 3 х + 5 =(2 х 4)Q(х) + 5 х + 5, (2 х 4)Q(х) = 2 х³ 3 х 5 х, откуда Q(х) = (2 х³ 8 х) : (2 х 4). Р(х) = 2 х³ 3 х + 5,М(х) = 2 х 4,R(х) = 5 х + 5.

21 Выполним деление:2 х³ 8 х 2 х 4 х²2 х³ 4 х² 4 х² 8 х + 2 х 4 х² 8 х 0 Ответ: Q(х) = х² + 2 х.

22 Схема Горнера. Существенно сократить и упростить вычисления помогает один несложный приём сокращённого деления, называемый схемой Горнера (Горнер Вильямс Джордж английский математик ). Покажем его практическое применение на конкретном примере, затем запишем алгоритм

23 Многочлен 1 х³ 1 х² 8 х + 6 1) разделить на х 3 2) представить в виде произведения В n первых клетках второй её строки получаем коэффициенты частного, расположенные в порядке убывания степеней х; в (n + 1) - й клетке получаем остаток от деления. х³ х² 8 х + 6 = (х 3) (х² + 2 х 2). а 1 а 1 b2b2 а 2 а 2 а 3 а 3 а 0 а 0 b1b1 b0b0 R Построенная таблица и называется схемой Горнера.

24 Схема Горнера. 1. В верхней строке таблицы записываем коэффициенты при х, располагая их в порядке убывания степеней, если соответствующая порядку степень отсутствует, то соответствующий коэффициент равен Перед таблице записываем известный целый корень многочлена. 3. Нижнюю строку таблицы заполняем по правилу: а) значение первого коэффициента переписываем; б) в каждой следующей клетке записываем число, равное сумме коэффициента, стоящего над ним и произведения числа, расположенного перед таблицей, на число находящееся в соседней слева клетке.

В данной статье будут рассмотрены рациональные дроби, ее выделения целых частей. Дроби бывают правильными и неправильными. Когда в дроби числитель меньше знаменателя – это правильная дробь, а неправильная наоборот.

Рассмотрим примеры правильных дробей: 1 2 , 9 29 , 8 17 , неправильных: 16 3 , 21 20 , 301 24 .

Будем вычислять дроби, которые могут сократиться, то есть 12 16 - это 3 4 , 21 14 - это 3 2 .

При выделении целой части производится процесс деления числителя на знаменатель. Тогда такая дробь может быть представлена как сумма целой и дробной части, где дробная считается отношением остатка от деления и знаменателя.

Найти остаток при делении 27 на 4 .

Решение

Необходимо произвести деление столбиком, тогда получим, что

Значит, 27 4 = ц е л а я ч а с т ь + о с т а т о к з н а м е н а т е л ь = 6 + 3 4

Ответ: остаток 3 .

Произвести выделение целых частей 331 12 и 41 57 .

Решение

Производим деление знаменателя на числитель при помощи уголка:

Производим деление далее и получаем, что

Поэтому имеем, что 331 12 = 27 + 7 12 .

Вторая дробь является правильной, значит, целая часть равняется нулю.

Ответ: целые части 27 и 0 .

Рассмотрим классификацию многочленов, иначе говоря, дробно-рациональную функцию. Ее считают правильной, когда степень числителя меньше степени знаменателя, иначе ее считают неправильной.

Деление многочлена на многочлен происходит по принципу деления углом, а представление функции как сумма целой и дробной частей.

Чтобы разделить многочлен на линейный двучлен, используется схема Горнера.

Произвести деление x 9 + 7 x 7 - 3 2 x 3 - 2 на одночлен 2 x 2 .

Решение

Воспользовавшись свойством деления, запишем, что

x 9 + 7 x 7 - 3 2 x 3 - 2 2 x 2 = x 9 2 x 2 + 7 x 7 2 x 2 - 3 2 x 3 2 x 2 + x 2 2 x 2 - 2 2 x 2 = = 1 2 x 7 + 7 2 x 5 - 3 4 x + 1 2 - 2 2 x - 2 .

Зачастую такого вида преобразования выполняются при взятии интегралов.

Произвести деление многочлена на многочлен: 2 x 3 + 3 на x 3 + x .

Решение

Знак деления можно записать в виде дроби вида 2 x 3 + 3 x 3 + x . Теперь необходимо выделить целую часть. Производим это при помощи деления столбиком. Получаем, что

Значит, получаем, что целая часть имеет значение - 2 x + 3 , тогда все выражение записывается как 2 x 3 + 3 x 3 + x = 2 + - 2 x + 3 x 3 + x

Разделить и найти остаток от деления 2 x 6 - x 5 + 12 x 3 - 72 x 2 + 3 на x 3 + 2 x 2 - 1 .

Решение

Зафиксируем дробь вида 2 x 6 - x 5 + 12 x 3 - 72 x 2 + 3 x 3 + 2 x 2 - 1 .

Степень числителя больше, чем у знаменателя, значит, что у нас имеется неправильная дробь. При помощи деления столбиком выдели целую часть. Получаем, что

Произведем деление еще раз и получим:

Отсюда имеем, что остаток равняется - 65 x 2 + 10 x - 3 , отсюда следует:

2 x 6 - x 5 + 12 x 3 - 72 x 2 + 3 x 3 + 2 x 2 - 1 = 2 x 3 - 5 x 2 + 10 x - 6 + - 65 x 2 + 10 x - 3 x 3 + 2 x 2 - 1

Существуют случаи, где необходимо дополнительно выполнять преобразование дроби для того, чтобы можно было выявить остаток при делении. Это выглядит следующим образом:

3 x 5 + 2 x 4 - 12 x 2 - 4 x 3 - 3 = 3 x 2 x 3 - 3 - 3 x 2 x 3 - 3 + 3 x 5 + 2 x 4 - 12 x 2 - 4 x 3 - 3 = = 3 x 2 x 3 - 3 + 2 x 4 - 3 x 2 - 4 x 3 - 3 = 3 x 2 + 2 x 4 - 3 x 2 - 4 x 3 - 3 = = 3 x 2 + 2 x x 3 - 3 - 2 x x 3 - 3 + 2 x 4 - 3 x 2 - 4 x 3 - 3 = = 3 x 2 + 2 x ( x 3 - 3 ) - 3 x 2 + 6 x - 4 x 3 - 3 = 3 x 2 + 2 x + - 3 x 2 + 6 x - 4 x 3 - 3

Значит, что остаток при делении 3 x 5 + 2 x 4 - 12 x 2 - 4 на x 3 - 3 дает значение - 3 x 2 + 6 x - 4 . Для быстрого нахождения результата применяют формулы сокращенного умножения.

Произвести деление 8 x 3 + 36 x 2 + 54 x + 27 на 2 x + 3 .

Решение

Запишем деление в виде дроби. Получим, что 8 x 3 + 36 x 2 + 54 x + 27 2 x + 3 . Заметим, что в числителе выражение можно сложить по формуле куба суммы. Имеем, что

8 x 3 + 36 x 2 + 54 x + 27 2 x + 3 = ( 2 x + 3 ) 3 2 x + 3 = ( 2 x + 3 ) 2 = 4 x 2 + 12 x + 9

Заданный многочлен делится без остатка.

Для решения используется более удобный метод решения, причем деление многочлена на многочлен считается максимально универсальным, поэтому часто используемым при выделении целой части. Итоговая запись должна содержать полученный многочлен от деления.

для успешной сдачи ОГЭ и ЕГЭ по математики важно умение делить многочлены – это может заметно упростить решение задачи, но данная тема в школьной программе отсутствует. Поэтому изучение теории делимости многочленов уже в текущих классах может помочь мне при решении алгебраических задач.

Задание №21 ОГЭ

Разложим числитель на множители, используя метод группировки:

Приведём другое решение.

Последовательно разделим многочлен на одночлены в столбик:

Проблема: В школьной программе отсутствует тема деления многочленов, однако это знание может помочь при решении математических уравнений и задач.

Способы решения проблемы:

Цель: Изучение способов и свойств деления многочленов.

Задачи проекта:

1. Изучить основные понятия, теоремы и алгоритмы теории делимости;

2. Подобрать задачи и алгоритмы их решения для учащихся 7-8 классов на применение теории делимости многочленов; 3. Создать буклет-справочник для ежедневного использования.

Методы: Анализ научной литературы.

Продукт: Математический справочник на основе полученных знаний.

Ресурсы: Полученная информация, бумага, деньги.

Планируемый результат:

Этье́н Безу́, французский математик, член Французской академии наук.

Дата рождения: 31 марта 1730 г

Место рождения: страна Франция, Немур.

Дата смерти:27 сентября 1783.

Научная сфера: теория чисел.

Теорема Безу

Остаток от деления многочлена f(x ) на многочлен (x-c) равен f(c ).

Степень остатка меньше 1, следовательно, остаток — константа. Пусть r-остаток

Это равенство верно при любых значениях х, положим х = а

Что и требовалось доказать

Важнейшим следствием теоремы Безу является то, что корни целочисленного многочлена являются делителями его свободного члена

Горнер Уильям Джордж

Горнер Уильям Джордж (1786 - 1837) — английский математик. Родился в городе Бристоль в Англии. Получил образование в Кингствудской школе Бристоля. Основал свою собственную школу в 1809 году в Бате.

Многочлены от одной переменной

р(x) = a n x n + a n-1 x n-1 +…+ a 3 x 3 + a 2 x 2 + a 1 x + a o

- стандартный вид многочлена р(х)

a n x n – старший член многочлена р(х)

a n – коэффициент при старшем члене

n – степень многочлена

a о – свободный член многочлена р(х)

Если a n = 1 , то многочлен р(х) называется приведенным

Если a n ≠ 1 , то многочлен р(х) называется неприведенным

Свойства делимости многочленов

1. Если многочлен P( x ) делится на многочлен Q( x ), а многочлен Q( x ) делится на многочлен M( x ) , то многочлен P( x ) делитcя на многочлен M( x )

2. Если многочлены P( x ) и Q( x ) делятся на многочлен M( x ), то многочлены

P( x ) + Q( x ) и P( x )  Q( x ) делятся на многочлен M( x )

Если P(x) делится на Q(x); а T(x) – произвольный многочлен; то P(x) . T(x) делится на Q(x);

4. Если ненулевой многочлен P(x) делится на Q(x), то deg P(x) ≥ deg Q(x),где deg(Р(x) и Q(x)-степени этих многочленов.

5. Еесли deg P(x) = deg Q(x); то P(x) делится на Q(x) тогда и только тогда, когда эти многочлены пропорциональны.

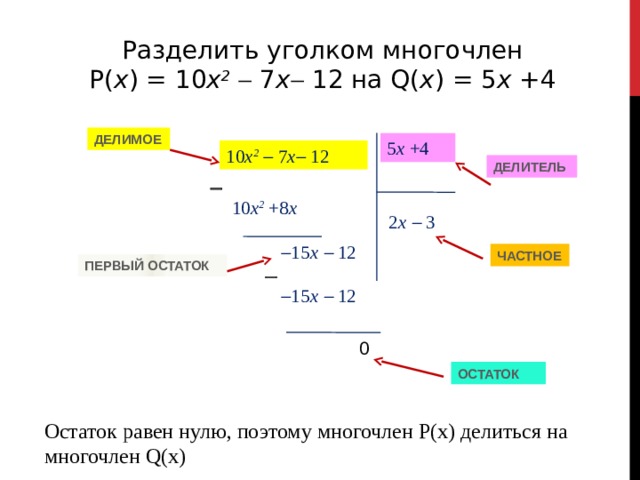
Разделить уголком многочлен

P( x ) = 10 x 2  7 х  12 на Q( x ) = 5 х +4

10 x 2  7 х  12

10 x 2 +8 х

2 х  3

 15 х  12

ПЕРВЫЙ ОСТАТОК

 15 х  12

Остаток равен нулю, поэтому многочлен P(x) делиться на многочлен Q(x)

Пример : Разделить многочлен P( x ) = 3 x 4 + 2 x 2 – 1 на многочлен

Q( x ) = x 2 + x .

3 x 4 + 2 x 2 – 1

x 2 + x

3 x 4 + 3 x 3

3 x 2 – 3 х + 5

– 3 x 3 + 2 х 2 – 1

– 3 x 3 – 3 x 2

5 x 2 – 1

5 x 2 + 5 x

– 5 x – 1

Степень остатка – 5 x – 1 меньше степени делителя x 2 + x, деление закончено.

Ответ: 3 x 2 – 3 х + 5  частное, – 5 x – 1  остаток.

2 п 2 -11 п +13

При каких натуральных значениях п выражение

является целым числом?

Разделим числитель дроби на знаменатель с остатком:

_2 п2 -11 п +13 п -3

2 п2 -6 п 2 п -5

_-5 п +13

-5 п +15

Таким образом, исходное выражение равно 2 п -5- , что

п -3

является целым числом тогда и только тогда, когда 2

нацело делится на п -3 . поскольку целыми делителями

числа 2 являются числа -2,

-1, 1, 2 и только они, получаем п =1, 2, 4, 5.

Ответ: п =1, 2, 4, 5.

Расположить делимое и делитель в убывающих степеняхх;
Разделить старший член делимого на старший член делителя; затем полученный одночлен сделать первым членом частного;
Первый член частного умножить на делитель, результат вычесть из делимого; полученная в результате разница является первым остатком;
Чтобы получить следующий член частного, нужно с первым остатком поступить так, как поступали с делимым и делителем в пунктах 2 и 3.
Это следует продолжать до тех пор, пока не будет получен остаток, равный нулю или остаток, степень которого меньше степени делителя.

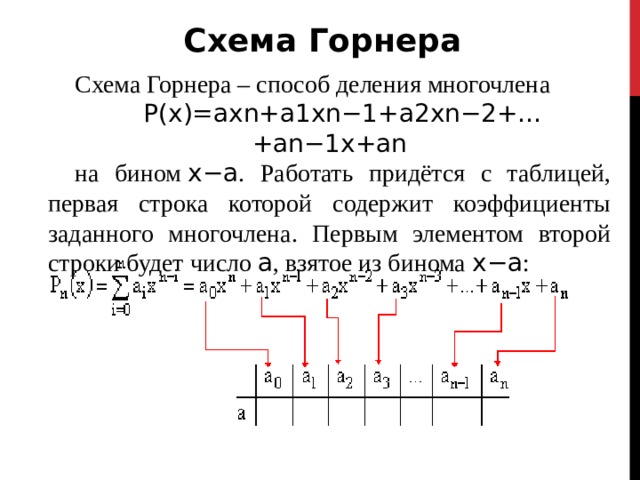
Схема Горнера

Схема Горнера – способ деления многочлена

P ( x )= axn + a 1 xn −1+ a 2 xn −2+…+ an −1 x + an

на бином x − a . Работать придётся с таблицей, первая строка которой содержит коэффициенты заданного многочлена. Первым элементом второй строки будет число a , взятое из бинома x − a :

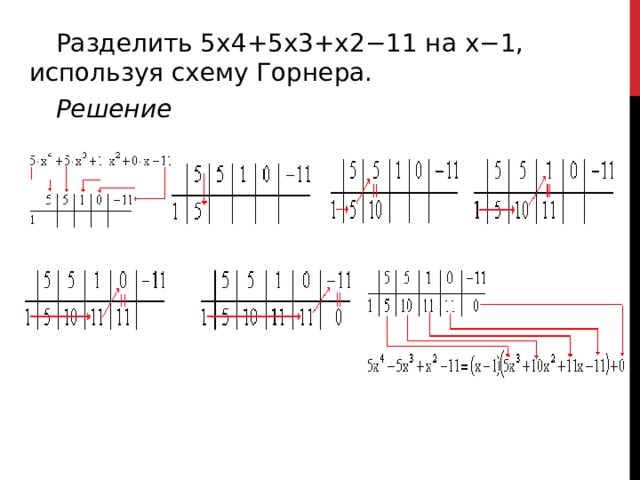
Разделить 5x4+5x3+x2−11 на x−1, используя схему Горнера.

Можно записывать решение покороче при помощи таблицы:

5 x 4 +5 x 3 + x 2 −11 делим на х – 1

Записать ответ: 5 x 4 +5 x 3 + x 2 −11 = ( 5 x 3 +10 x 2 +11 x +11 ) (х – 1) + 0

Читайте также: