Степенная функция в экономике доклад

Обновлено: 07.07.2024

Целью курсовой работы является рассмотрение понятия функции и изучение ее свойств в применении к задачам экономики.
Задачи курсовой работы:
- раскрыть понятие функции;
- изучить основные свойства функций (периодичность, монотонность и т.д.);
- исследовать примеры применения функций в экономике;
- раскрыть понятие производной функции;
- изучить понятие функции нескольких переменных и ее значение в экономике.

Содержание

Введение 3
Глава 1. Числовые функции 6
§1.1. Понятие числовой функции, графики функции, обратной функции 6
§1.2. Четные и нечетные функции 9
§1.3. Периодичность функции 10
§1.4. Монотонность функции 10
§1.5. Выпуклость функции 11
§1.6. Дробно-линейные функции 13
§1.7. Непрерывность функции 14
§1.8. Применение функций в экономике 16
§1.9. Производная функции 21
§1.10. Экономический смысл производной. Использование понятия производной в экономике 21
Глава 2. Функции нескольких переменных 25
§1.1. Основные понятия 25
§1.2. Функции нескольких переменных в экономической теории 27
Заключение 31
Список использованной литературы 34

Вложенные файлы: 1 файл

Применение функций в экономике 03.06.docx

Глава 1. Числовые функции

§1.1. Понятие числовой функции, графики функции, обратной функции

§1.2. Четные и нечетные функции

§1.3. Периодичность функции

§1.4. Монотонность функции

§1.5. Выпуклость функции

§1.6. Дробно-линейные функции

§1.7. Непрерывность функции

§1.8. Применение функций в экономике

§1.9. Производная функции

§1.10. Экономический смысл производной. Использование понятия производной в экономике

Глава 2. Функции нескольких переменных

§1.1. Основные понятия

§1.2. Функции нескольких переменных в экономической теории

Список использованной литературы

В экономических исследованиях издавна применялись простейшие математические методы. В хозяйственной жизни широко используются геометрические формулы. Так, площадь участка поля определяется путем перемножения длины на ширину или объем силосной траншеи - перемножением длины на среднюю ширину и глубину. Существует целый ряд формул и таблиц, облегчающих хозяйственным работникам определение тех или иных величин.

При изучении природных явлений, процессов, обусловленных деятельностью человека, приходится рассматривать изменение одной величины в зависимости от изменения другой, описывая эти изменения функциональными зависимостями.

Понятие величины настолько широко и всеобъемлюще, что ему трудно дать точное определение. Массы, давления, работы, заряды, длины и объемы, целые и дробные числа – все это примеры величин. На первой стадии величиной можно считать то, что выраженное в определенных единицах, характеризуется своим числовым значением (например, масса – в граммах или тоннах и т.п.).

За последние годы многие понятия, ранее воспринимавшиеся лишь качественно (такие, например, как эффективность, количество информации) переведены в разряд величин. Каждый такой перевод дает возможность применить к указанным понятиям количественный математический анализ, что часто оказывается очень эффективным.

Современная экономическая наука характеризуется широким использованием математики. Математические методы стали составной частью методов любой экономической науки, включая экономическую теорию. Ее использование в единстве с обстоятельным экономическим анализом и новыми информационными технологиями открывает новые возможности для экономической науки и практики.

Актуальность изучения математических методов в экономике обусловлена тем, что современная экономическая теория предполагает существенно более высокий уровень формализации, чем это было принято в отечественной высшей школе.

Объектом исследования курсовой работы являются математические методы, применяемые при решении задач экономики.

Предметом исследования курсовой работы являются числовые функции и их свойства, практические примеры их использования в экономике.

Целью курсовой работы является рассмотрение понятия функции и изучение ее свойств в применении к задачам экономики.

Задачи курсовой работы:

- раскрыть понятие функции;

- изучить основные свойства функций (периодичность, монотонность и т.д.);

- исследовать примеры применения функций в экономике;

- раскрыть понятие производной функции;

- изучить понятие функции нескольких переменных и ее значение в экономике.

При написании работы использовались учебники по высшей математике и математическому анализу таких авторов, как В.А. Зорич, Н.Ш. Кремер, Б.А. Путко, М. С. Красс, Б.П. Чупрынов, Л.Д. Кудрявцев, Р.З. Гильмутдинов, В.А. Ильин, Э.Г.Позняк, А.С. Солодовников, В.А. Малугин и др.; интернет-ресурсы (примеры, задачи, поиск литературы), а также учебники-практикумы по экономике.

Математические методы являются важнейшим инструментом анализа экономических явлений и процессов, построения теоретических моделей, позволяющих отобразить существующие связи в экономической жизни, прогнозировать поведение экономических субъектов и экономическую динамику. Математическое моделирование становится языком современной экономической теории, одинаково понятным для учёных всех стран мира.

Презентация по теме "Показательная функция" и ее применение в различных областях науки и техники.

Вложение	Размер
pokazatelnaya_funktsiya_i_ee_primenenie.ppt	1.07 МБ

Предварительный просмотр:

Подписи к слайдам:

Показательная функция. Функция вида у=а х ,где а-заданное число, а > 0, а ≠ 1, х-переменная, называется показательной.

Показательная функция обладает следующими свойствами: Д(у): множество R всех действительных чисел; Е(у):множество всех положительных чисел; Показательная функция у=а х является возрастающей на множестве всех действительных чисел,если а>1 ,и убывающей,если 0 1 ,то функция выпукла вниз.

Графики функции у=2 х и у=(½) х График функции у=2 х проходит через точку (0;1) и расположен выше оси Ох. а>1 Д(у): х є R Е(у): у > 0 Возрастает на всей области определения. График функции у= также проходит через точку (0;1) и расположен выше оси Ох. 0 0 Убывает на всей области определения.

Показательные уравнения. Уравнения,у которых неизвестное находится в показателе степени, называются показательными. Способы решения: По свойству степени; Вынесение общего множителя за скобки; Деление обеих частей уравнения на одно и то же выражение,принимающее значение отличное от нуля при всех действительных значениях х; Способ группировки; Сведение уравнения к квадратному; Графический. . Например:

Используя свойства возрастания и убывания показательной функции, можно сравнить числа и решать показательные неравенства. Сравнить: а) 5 3 и 5 5 ; б) 4 7 и 4 3 ; в) 0,2 2 и 0,2 6 ; г) 0,9 2 и 0,9. Решить: а) 2 х >1; б) 13 х+1 0,7; г) 0,04 х а в или а х 1, то х>в (х в) .

Способы решения показательных неравенств. 1. По свойству степени; 2. Вынесение общего множителя за скобки; 3.Сведение к квадратному; 4. Графический. Некоторые показательные неравенства заменой а х = t сводятся к квадратным неравенствам,которые решают,учитывая,что t > 0. х у

Решение систем показательных уравнений и неравенств.

Показательная функция И её применение в природе и технике.

Наглядный бытовой пример! Все, наверное, замечали, что если снять кипящий чайник с огня, то сначала он быстро остывает, а потом остывание идет гораздо медленнее. Дело в том, что скорость остывания пропорциональна разности между температурой чайника и температурой окружающей среды. Чем меньше становится эта разность, тем медленнее остывает чайник. Если сначала температура чайника равнялась То, а температура воздуха T1, то через t секунд температура Т чайника выразится формулой: T=(T1-T0)e-kt+T1, где k - число, зависящее от формы чайника, материала, из которого он сделан, и количества воды, которое в нем находится.

Когда радиоактивное вещество распадется, его количество уменьшается. Через некоторое время остается половина первоначального количества вещества. Этот промежуток времени to называется периодом полураспада. Вообще через t лет масса m вещества будет равна: m=m0(1/2)t/t0, где m0 - первоначальная масса вещества. Чем больше период полураспада, тем медленнее распадается вещество. Явление радиоактивного распада используется для определения возраста археологических находок, например, определен примерный возраст Земли, около 5,5 млрд. лет, для поддержания эталона времени.

Задача: Период полураспада плутония равен 140 суткам. Сколько плутония останется через 10 лет, если его начальная масса равна 8г ? m = ? Ответ: 1,13 •10 -7 (г).

Как видите, во всех приведенных выше исследованиях использовалась показательная функция.

Вот некоторые из Нобелевских лауреатов, получивших премию за исследования в области физики с использованием показательной функции: Пьер Кюри - 1903 г. Ричардсон Оуэн - 1928 г. Игорь Тамм - 1958 г. Альварес Луис - 1968 г. Альфвен Ханнес - 1970 г. Вильсон Роберт Вудро - 1978 г.

Она не перестаёт нас удивлять! Показательная функция также используется при решении некоторых задач судовождения, например, функцию е-x используют в задачах, требующих применения биноминального закона (повторение опытов), закона Пуассона (редких событий), закона Релея (длина случайного вектора).

Применение показательной функции в биологии .

Применение логарифмической функции в биологии. В питательной среде бактерия кишечной палочки делится каждую минуту. Понятно, что общее число бактерий за каждую минуту удваивается. Если в начале процесса была одна бактерия, то через х минут их число ( N ) станет равной 2 х , т.е. N ( х ) = 2 х .

Применение показательной функции в экономике.

Задача: Ежемесячно на банковский вклад, равный S 0 рублей начисляется р%. На сколько процентов возрастет банковский вклад за х месяцев? Решение. Пусть р = 2%, х = 12 месяцев. Тогда за год банковский вклад возрастет на Ответ: на 27%.

Автор работы награжден дипломом победителя III степени

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке "Файлы работы" в формате PDF

Целью моей работы является исследование сфер применения показательной функции.

Объект исследования: показательная функция.

Показательная функция часто применяется в физике, химии, биологии, географии, экономике и иных науках.

Рост количества бактерий, концентрация адреналина в крови, способность почек выводить из крови радиоактивные изотопы, восстановление концентрации гемоглобина в крови, рост количества древесины, количество радиоактивного вещества, изменение количества населения – все это измеряется по законам показательной функции.

В жизни нередко приходиться встречаться с такими фактами, когда скорость изменения какой-либо величины пропорциональна самой величине. В этом случает рассматриваемая величина будет изменяться по закону, имеющему вид y=y0ax

Практическая значимость работы заключается в том, что она позволяет объективно оценить значимость показательной функции, основываясь на рассмотренных фактах, раскрывая особенности применения показательной функции в современной жизни человека.

Материал исследовательской работы может быть использован в форме презентации для выступления различных публичных мероприятиях, в школе; для публикации в печатных изданиях (в научно-популярной литературе), размещения данных о проекте на сайте нашей школы и других сайтах определенной тематики.

Подбор, изучение, анализ информации о функциях, в частности, показательной функции.

Анкетирование с целью узнать, насколько люди осведомлены о сфере применения показательной функции.

Исследование свойств показательной функции.

Примеры применения показательной функции.

Задачи на показательную функцию.

Доказать, что функциональные зависимости существуют во всех сферах жизни;

Расширить знания о показательной функции и методах решения уравнений;

Узнать, какие явления из жизни и некоторых наук описывает показательная функция;

Научиться применять полученные знания в нестандартных ситуациях на основе рассмотрения примеров из реальной жизни, при решении практико-ориентированных задач.

Функция - одно из основных математических и общенаучных понятий. Оно сыграло и поныне играет большую роль в познании реального мира.

Начиная лишь с 17 века, в связи с проникновением в математику идеи переменных, понятие функции применяется явно и вполне сознательно.

Путь к появлению понятия функции заложили в 17 веке французские ученые Франсуа Виет (1540-1603) и Рене Декарт (1596-1650);

Они разработали единую буквенную математическую символику, которая вскоре получила всеобщее признание.

3.1 Аналитическое определение функции.

Готфрид Вильгельм Лейбниц (1646-1716)

Большой вклад в разрешение спора Эйлера, Даламбера, Бернулли и других ученых 18 века по поводу того, что стоит понимать под функцией, внес французский математик Жан Батист Жозеф Фурье.

Из трудов Фурье следовало, что любая кривая независимо от того, из скольких и каких разнородных частей она состоит, может быть представлена в виде единого аналитического выражения и что имеются также прерывные кривые, изображаемые аналитическим выражением.

Жан Батист Жозеф Фурье4.1 Примеры применения показательной функции

Так утверждал великий ученый, математик Леонард Эйлер. И он был в корне прав, говоря о том, что показательная функция применятся во многих сферах жизни человека.

Кроме того, перед началом исследования, мною был проведен опрос с целью узнать, осведомлены ли люди о том, что такое показательная функция и где она применяется:

В итоге, 72% опрошенных не знают, где применяется данная функция. Но в своем исследовании я решила рассказать, где же используется данная функция.

Приведем примеры, где мы сталкиваемся с показательной функцией в повседневной жизни, а также как она применяется на практике.

Напомним вид показательной функции: у=а х , где а>0, а≠1, x Є R. Показательная функция встречается в самых различных областях науки - в физике, химии, биологии, экономике.

A-изменение количества древесины во времени; A₀-начальное количество древесины; t-время; k, а - некоторые постоянные.

2. Давление воздуха убывает с высотой по закону P=P₀*a -kh , где P- давление на высоте h, P₀ - давление на уровне моря, а- некоторая постоянная.

Процессы выравнивания (именно так называют процессы, изменяющиеся по законам показательной функции) часто встречаются и в биологии.

3. Рост количества бактерийпроисходит по закону N=5 t , где N-число колоний бактерий в момент времени t;

Это закон органического размножения: при благоприятных условиях (отсутствие врагов, большое количество пищи) живые организмы размножались бы по закону показательной функции.

Также вспомним что, при испуге в кровь внезапно выделяется адреналин, который потом разрушается, причем скорость разрушения примерно пропорциональна количеству этого вещества, еще остающемуся в крови. При диагностике почечных болезней часто определяют способность почек выводить из крови радиоактивные изотопы, причем их количество в крови падает по показательному закону.

Примером обратного процесса может служить восстановление концентрации гемоглобина в крови у донора или у раненого, потерявшего много крови. В этом случае по показательному закону убывает разность между нормальным содержанием гемоглобина и имеющимся количеством этого вещества.

4. Количество радиоактивного вещества, оставшегося к моменту t,

описывается формулой , где No – первоначальное количество вещества,

T_1/2– период полураспада.

5. Площадь сечения троса связана с сопротивлением разрыва также по показательному закону.

Сейчас многие моря и океаны бороздят исследовательские корабли. В заранее установленных местах они останавливаются и спускают за борт трос, на конце которого находятся приборы. Их опускают на дно, а потом поднимают наверх и записывают показания. Но иногда происходит печальное событие — трос разрывается и все ценные приборы оказываются погребенными на дне моря.

Казалось бы, этой беды можно было бы избежать, сделав трос потолще. Но тут возникает новое осложнение — верхние части троса должны удерживать не только спускаемые приборы, но и нижнюю часть самого троса, а потому при утолщении всего троса на верхнюю часть ляжет слишком большая нагрузка.

Поэтому целесообразно делать нижнюю часть троса тоньше, чем верхнюю. Возникает вопрос: как должна меняться толщина троса для того, чтобы в любом его сечении на 1 см2 приходилась одна и та же нагрузка?

Исследование этого вопроса показало, что площадь сечения троса должна изменяться по следующему закону: , где

So — площадь его нижнего сечения,

S — площадь сечения на высоте х от нижнего сечения,

γ — удельный вес материала, из которого сделан трос,

Р — вес в воде опускаемого груза (нам пришлось написать в формуле γ — 1 вместо γ, так как и материал троса теряет в воде вес по закону Архимеда).

Такой трос называют тросом равного сопротивления разрыву.

6. Процесс изменения температуры чайника при кипении выражается формулой:

Все, наверное, замечали, что если снять кипящий чайник с огня, то сначала он быстро остывает, а потом остывание идет гораздо медленнее. Дело в том, что скорость остывания пропорциональна разности между температурой чайника и температурой окружающей среды. Чем меньше становится эта разность, тем медленнее остывает чайник. Если сначала температура чайника равнялась То, а температура воздуха T1, то через t секунд температура Т чайника выразится формулой: T=(T1-T0)e-kt+T1,где k - число, зависящее от формы чайника, материала, из которого он сделан, и количества воды, которое в нем находится.

7. При падении тел в безвоздушном пространстве скорость их непрерывно возрастает. При падении тел в воздухе скорость падения тоже увеличивается, но не может превзойти определённой величины.

8. При прохождении света через мутную среду каждый слой этой среды поглощает строго определенную часть падающего на него света. Сила света I определяется по формуле: I = I₀e -ks , где

s – толщина слоя;

k – коэффициент, характеризующий мутную среду

В ходе проведения исследований данного материала, анализа информации, моя гипотеза о том, что функциональные зависимости существуют во всех сферах жизни, подтверждена.

Также мы расширили знания о показательной функции, изучили свойства показательной функции, узнали многое об истории развития понятия функции.

К степенным функциям в теории относятся следующие виды:

линейная функция \(y = kx + b\) ;
квадратичная парабола \(y = x^\) (в общем виде: \(y = ax^ + bx + c)\) ;
кубическая парабола \(y = x^\) ;
гипербола \(y = \frac\) , которую можно представить в виде \( y = x^;\)
функция \(y =\sqrt\) , так как \(\sqrt = x^<\frac>.\)

В качестве примера можно рассмотреть описание функции: \(y=x^>\) . В первую очередь следует проанализировать функции с показателем степени \(\frac>1\) . Например, задана некая функция:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Исходя из обозначения, при x≥0, область определения рассматриваемой функции – это луч [0;+∞).

Далее следует записать таблицу значений:

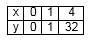
Затем можно сравнить несколько степенных функции следующим способом:

Число 2,5 находится между 2 и 3. В таком случае можно предположить, что и график рассматриваемой функции расположен между соответствующими графиками. Можно представить разные характеристики х, чтобы сравнить значения функций, которые зависят от x:

При \(0 , получается \(x^6 , но и выполняется \(\sqrt или \(x^3

При \(x>1\) , получается \(x^4 , но и выполняется \(\sqrt или \(x^2

Все графики целесообразно построить на одном рисунке. В первом случае \(0 :

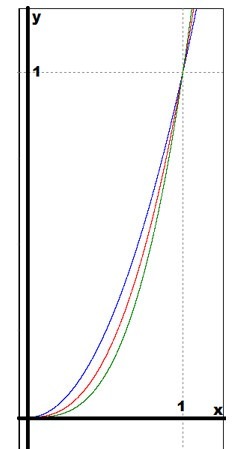
В данном случае синий цвет соответствует функции \(y=x^2\) ; красный: \( y=x^\) ; зеленый: \(y=x^3\) . На следующем этапе нужно построить графики по порядку на всей области определения функции \(y=x^\) . Цвет графиков останется прежним, как и на предыдущем рисунке:

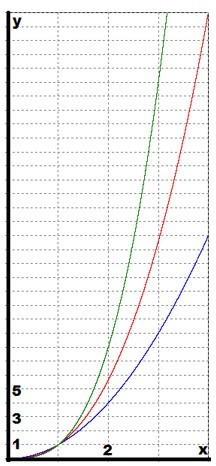
График функции \(y=x^>\) , \((m>n)\) является кривой, которая проходит через точки (0,0) и (1,1), и напоминает ветвь параболы. При увеличении показателя график функции в верхнем положении становится круче.

Линейная функция y = kx + b. Графиком данной функции является прямая линия. Для того, чтобы ее построить, требуется пара точек. При k > 0, линейная функция будет расти. При увеличении k график становится круче. Значение k представляет собой угловой коэффициент прямой и равно тангенсу угла наклона рассматриваемой прямой к положительному направлению оси X:

При использовании k

При k = 0, на графике будет изображена прямая y = b, которая параллельна оси X. В том случае, когда имеет место равенство угловых коэффициентов прямых, прямые будут параллельны друг другу.

Квадратичная функция \(y = ax2 + bx + c\) представляет собой параболу. Она обладает рядом особенностей:

Функция \(y = x^\) является кубической параболой. Можно представить ее на рисунке, а также функции \( y = x^\) и \(y = x^.\)

Можно отметить, что функции \(y = x^\) и \(y = x^\) обладают некоторыми сходствами. Графики являются симметричными по отношению к оси Y. В данном случае можно сказать, что рассматриваемые функции – четные.

Функция \(y = f(x)\) является четной, когда:

область определения функции симметрична относительно нуля;
каждое значение x из области определения соответствует справедливому равенству \(f(−x) = f(x)\) .

Графики функций \(y = x^\) и \(y = x^\) симметричны по отношению к началу координат. Данные функции являются нечетными.

Функция \(y = f(x)\) – нечетная, при условии, что:

область определения функции симметрична относительно нуля;
любой x из области определения соответствует равенству \(f(-x) = -f(x)\) .

Функция \(\small y = \frac\) в виде гиперболы также представляет собой степенную функцию. Это объясняется тем, что \(\small \frac = x^\) . Так как знаменатель не должен быть равен нулю, рассматриваемая функция не определена при \(x = 0\) . Гипербола представляет собой нечетную функцию с графиком, который симметричен по отношению к началу координат.

Построение графика функции \(\small y = \sqrt\) следует начинать с области определения. Выражение \(\small \sqrt\) определено при \(x ≥ 0\) . Поэтому областью определения функции являются все неотрицательные числа. Также \(\small y = \sqrt\) принимает только неотрицательные значения, поскольку \(\small \sqrt ≥ 0.\)

Целесообразно воспользоваться данными свойствами в процессе решения уравнений и неравенств. Уравнение вида \(\small \sqrt=g(x)\) имеет смысл только при \(f(x) ≥ 0\) и \(g(x) ≥ 0\) . Это является областью допустимых значений.

На одном графике можно построить параболу \( y = x^\) и функцию \(\small y = \sqrt\) . Следует рассмотреть правую ветвь параболы, при \(x ≥ 0\) . Заметим, что эта часть параболы и график функции \(\small y = \sqrt\) словно нарисованы по одному шаблону, по-разному расположенному в координатной плоскости. Они симметричны относительно прямой y = x.

То, что для одной из них является областью определения, для другой — представляет собой область значений. Данные функции носят название взаимно-обратных.

Виды и их свойства, область определения

Степенные функции обладают рядом специфических свойств, которые могут отличаться в зависимости от их вида. Рассмотрим основные из них.

D(y)=[0;+∞);
функцию нельзя отнести ни к четной, ни к нечетной;
возрастает на [0;+∞);
не имеет ограничений в верхней части, но ограничена в нижней;
отсутствует максимальное значение, минимальное значение равно нулю;
непрерывность;
E(f)=[0; +∞);
выпукла вниз.

В качестве примера можно рассмотреть случай, когда показатель степени является правильной дробью, у которой значение числителя меньше, чем знаменателя. График функции \( y=x^>\) , \((m>n)\) напоминает график функции \(y=\sqrt[n]\) :

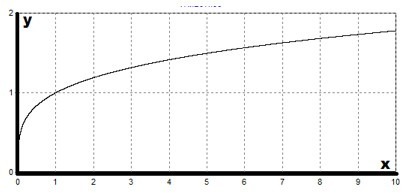
D(y)=[0;+∞);
нельзя отнести ни к четной, ни к нечетной;
возрастает на [0;+∞);
не имеет ограничений сверху, ограничена снизу;
максимальное значение отсутствует, наименьшее значение равно нулю;
непрерывность;
E(f)=[0; +∞);
выпукла вверх.

Далее следует ознакомиться с графиком функции \(y=x^>\) . Можно заметить, что он похож на гиперболу. График обладает двумя асимптотами:

График имеет следующий вид:

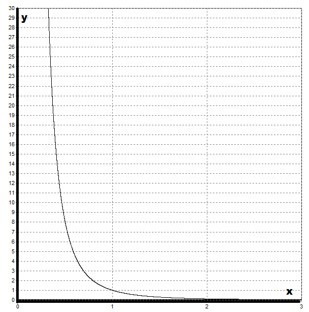
D(y)=(0;+∞);
не является ни четной, ни нечетной;
убывает на (0;+∞);
не ограничена в верхней части, обладает ограничением в нижней;
максимальное значение отсутствует, минимальное – ноль;
непрерывность;
E(f)=(0; +∞);
выпукла вниз.

В том случае, когда x>0, а r – какое-либо рациональное число, производная степенной функции \(y=x^r\) определяется, согласно формуле:

Степенная функция с рациональным и иррациональным показателем

Степень действительного числа a, обладающего рациональным показателем n вычисляется, согласно уравнению:

Функция \( f(x)=x^(r\in Q)\) представляет собой степенную функцию с рациональным показателем.

Степенью числа a, которое является положительным, c иррациональным показателем \(\alpha\) называется выражение вида \(a^\) со значением, равным пределу последовательности \(a^>\) , \(a^>, a^>\) , …, где \(\alpha_, \alpha_, \alpha_\) являются последовательными десятичными приближениями иррационального числа \(\alpha\) .

Функция \(f(x)=x^(r\in J)\) представляет собой степенную функцию с иррациональным показателем.

Как строить графики степенных функций

График функции является множеством точек, у которых абсциссы являются допустимыми значениями аргумента х, а ординаты – соответствующими значениями функции y.

Согласно определению, построить график какой-либо функции можно путем поиска всех пар соответствующих значений аргумента и функции. Как правило, в результате получается бесконечное множество точек, что затрудняет процесс построения графика. В связи с этим требуется исследовать функцию:

обозначить область определения и область изменения функции;
найти области ее убывания или возрастания;
определить асимптоты, интервалы знакопостоянства;
выявить несколько точек, принадлежащих графику;
соединить найденные точки плавной кривой.

Задачи со степенной функцией

Необходимо определить максимальное и минимальное значения для функции \(y=x^>\) на отрезке:

Показатель степени рассматриваемой функции обладает положительным значением. В этом случае, учитывая свойства записанной функции, можно заключить, что она возрастает на всей области определения. Таким образом, функция достигает своего максимума и минимума на концах заданных отрезков (если она определена в этих точках).

На промежутке (2,10) максимальное и минимальное значения функции отсутствуют, в связи с тем, что промежуток является открытым, и точки 0 и 4 к данному интервалу не относятся.

На луче [9;+∞) наибольшее значение отсутствует

Требуется определить максимальное и минимальное значение на отрезке [1;9] для функции:

Вычислим производную рассматриваемой функции:

Так как производная существует на всей области определения исходной функции, можно заключить, что критические точки отсутствуют.

Далее определим стационарные точки:

Заданному отрезку принадлежит только одно решение \(x_2=4\)

Построим таблицу значений нашей функции на концах отрезка и в точке экстремума:

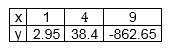
График функции \(y=x^>\) будет возрастать, а график функции \(у=24-х\) – убывать. Известно, что когда одна функция возрастает, а вторая убывает, то будет лишь одна точка, в которой эти функции пересекаются. Следовательно, уравнение обладает всего одним решением. Можно заметить, что:

Таким образом, при х=8 уравнение преобразуется в справедливое равенство: 16=16, что является ответом к задаче.

Необходимо построить график функции с объяснениями: \(y=(x-3)^\frac+2\)

График рассматриваемой функции можно получить из графика функции:

Требуется сместить этот график на 3 единицы в правую сторону и на 2 единицы вверх:

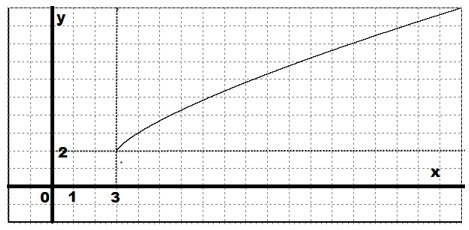
Требуется записать уравнение для касательной к прямой \(y=x^>\) в точке х=1.

Читайте также: