Построение логических функций по таблице истинности доклад
Обновлено: 02.07.2024
Логическим элементом называется дискретный преобразователь, который после обработки входных двоичных сигналов выдает на выходе сигнал, являющийся значением одной из логических операций.
Логические элементы компьютера оперируют сигналами, представляющими собой электрические импульсы. Есть импульс – логический смысл сигнала – 1, нет импульса – 0. На входы логического элемента поступают сигналы-значения аргументов, на выходе появляется сигнал-значение функции.
Преобразование сигнала логическим элементом задается таблицей состояния, которая фактически является таблицей истинности, соответствующей логической функции.
Рассмотрим условные обозначения (схемы) базовых логических элементов, реализующих логическое умножение (конъюнктор), логическое сложение (дизъюнктор) и отрицание (инвертор).
например,
например,
ИЛИ ДРУГОЙ ВИД ЛОГИЧЕСКИХ ЭЛЕМЕНТОВ
Устройства компьютера (сумматоры в процессоре, ячейки памяти в оперативной памяти и др.) строятся на основе базовых логических элементов.
Если элемент имеет входное напряжение от 0 до 0,4В, то оно рассматривается как логический 0, если напряжение в пределах от 0,7 до 1,5В, то оно рассматривается как 1. Примерно такие же характеристики имеет выходное напряжение.
Построить схемы
Пример 1. Составить схему
Пример 2. Составить схему
Пример 3. Составить схему
Пример 4. Составить схему
Пример 5. Составить схему
Пример 6. Составить схему
Пример 7. Составить схему
II. Выполним задачу обратную данной. Составим логическое выражение по заданной логической схеме:
Данное логическое выражение можно упростить.
Операция И - логическое умножение, ИЛИ - сложение. Запишем выражение, заменяя знаки & и U на * и + соответственно.
Упростим , затем запишем
и тогда логическая схема примет вид:
Вывод: Логические схемы, содержащие минимальное количество элементов, обеспечивают большую скорость работы и увеличивают надёжность устройства.
Алгебра логики дала конструкторам мощное средство разработки, анализа и совершенствования логических схем. Проще, и быстрее изучать свойства и доказывать правильность работы схемы с помощью выражающей её формулы, чем создавать реальное техническое устройство.
По заданной логической функции построить логическую схему.
Наше построение схемы, мы начнем с логической операции, которая должна выполняться последней. В нашем случае такой операцией является логическое сложение, следовательно, на выходе логической схемы должен быть дизъюнктор. На него сигналы будут подаваться с двух конъюнкторов, на которые в свою очередь подаются один входной сигнал нормальный и один инвертированный (с инверторов).

Пример 2. Выписать из логической схемы соответствующую ей логическую формулу:

Построение логических схем.
По заданной логической функции построить логическую схему и таблицу истинности.


2. Выписать из логической схемы соответствующую ей логическую формулу:

1. По заданной логической функции построить логическую схему и таблицу истинности.
Решение:


2. Выписать из логической схемы соответствующую ей логическую формулу:

По заданной логической функции построить логическую схему и таблицу истинности.
Перечислите основные логические операции.
Что такое логическое умножение?
Что такое логическое сложение?
Что такое инверсия?
Что такое таблица истинности?
Что такое сумматор?
Что такое полусумматор?
Информатика и информационные технологии. Учебник для 10-11 классов,Н. Д. Угринович – 2007г.;
2. Практикум по информатике и информационным технологиям. Учебное пособие для общеобразовательных учреждений, Н. Д. Угринович, Л. Л. Босова, Н. И. Михайлова – 2007г.
Эта лицензия позволяет другим редактировать, поправлять и брать за основу ваше произведение в некоммерческих целях до тех пор пока они указывают вас в качестве автора и лицензируют их новые творения на идентичных условиях.
Основы логики. Логические операции и таблицы истинности
На данной странице будут рассмотрены 6 логических операций: конъюнкция, дизъюнкция, инверсия, импликация, эквивалентность и исключающие или, которых вам будет достаточно для решения сложных логических выражений. Также мы рассмотрим порядок выполнения данных логических операций в сложных логических выражениях и представим таблицы истинности для каждой логической операции.
Высказывание - это повествовательное предложение, про которое можно определенно сказать истинно оно или ложно (истина (логическая 1), ложь (логический 0)).
Логические операции - мыслительные действия, результатом которых является изменение содержания или объема понятий, а также образование новых понятий.
Логическое выражение - устное утверждение или запись, в которое, наряду с постоянными величинами, обязательно входят переменные величины (объекты). В зависимости от значений этих переменных величин (объектов) логическое выражение может принимать одно из двух возможных значений: истина (логическая 1) или ложь (логический 0).
Сложное логическое выражение - логическое выражение, состоящее из одного или нескольких простых логических выражений (или сложных логических выражений), соединенных с помощью логических операций.
Конъюнкция - это сложное логическое выражение, которое считается истинным в том и только том случае, когда оба простых выражения являются истинными, во всех остальных случаях данное сложенное выражение ложно.
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
2) Логическое сложение или дизъюнкция:
Дизъюнкция - это сложное логическое выражение, которое истинно, если хотя бы одно из простых логических выражений истинно и ложно тогда и только тогда, когда оба простых логических выраженbя ложны.
Обозначение: F = A v B.
Таблица истинности для дизъюнкции
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
3) Логическое отрицание или инверсия:
Инверсия - это сложное логическое выражение, если исходное логическое выражение истинно, то результат отрицания будет ложным, и наоборот, если исходное логическое выражение ложно, то результат отрицания будет истинным. Другими простыми слова, данная операция означает, что к исходному логическому выражению добавляется частица НЕ или слова НЕВЕРНО, ЧТО.
Обозначение: F = ¬ A.
Таблица истинности для инверсии
| A | ¬ А |
| 1 | 0 |
| 0 | 1 |
4) Логическое следование или импликация:
Импликация - это сложное логическое выражение, которое истинно во всех случаях, кроме как из истины следует ложь. То есть данная логическая операция связывает два простых логических выражения, из которых первое является условием (А), а второе (В) является следствием.
Обозначение: F = A → B.
Таблица истинности для импликации
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
5) Логическая равнозначность или эквивалентность:
Эквивалентность - это сложное логическое выражение, которое является истинным тогда и только тогда, когда оба простых логических выражения имеют одинаковую истинность.
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
6) Операция XOR (исключающие или)
Обозначение: F = A ⊕ B .
| A | B | F |
| 1 | 1 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
Порядок выполнения логических операций в сложном логическом выражении
1. Инверсия;
2. Конъюнкция;
3. Дизъюнкция;
4. Импликация;
5. Эквивалентность.
Для изменения указанного порядка выполнения логических операций используются скобки.
Таблицы истинности можно составить и для произвольной логической функции F(a, b, c…).
В общем случае таблицы истинности имеют размер 2 N строк комбинаций для N независимых логических переменных.
Поскольку таблица истинности выражения состоит из строк со всеми возможными комбинациями значений переменных, она полностью определяет значение выражения.
Законы алгебры логики
Те, кому лень учить эти законы, должны вспомнить алгебру, где знание нескольких способов преобразования позволяет решать очень сложные уравнения.
Строго говоря, это не законы, а теоремы. Но их доказательство не входит в программу изучения. Впрочем, доказательство обычно основывается на построении полной таблицы истинности.
Замечание. Знаки алгебры логики намеренно заменены на сложение и умножение.
Замена операций импликации и эквивалентности
Операций импликации и эквивалентности иногда нет среди логических операций конкретного компьютера или транслятора с языка программирования. Однако для решения многих задач эти операции необходимы. Существуют правила замены данных операций на последовательности операций отрицания, дизъюнкции и конъюнкции.
Так, заменить операцию импликации можно в соответствии со следующим правилом:
A → B = ¬ A \/ B
Для замены операции эквивалентности существует два правила:
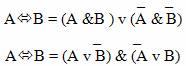
В справедливости данных формул легко убедиться, построив таблицы истинности для правой и левой частей обоих тождеств.

ГОСТ
Логическая функция – функция, переменные которой принимают одно из двух значений: $1$ или $0$.
Любую логическую функцию можно задать с помощью таблицы истинности: набор всех возможных аргументов записывается в левой части таблицы, а соответствующие значения логической функции – в правой части.
Таблица истинности – таблица, которая показывает, какие значения примет составное выражение при всех возможных наборах значений простых выражений, входящих в него.
При составлении таблицы истинности важно учитывать следующий порядок выполнения логических операций:

Приоритетом в выполнении порядка выполнения операций пользуются скобки.
Алгоритм построения таблицы истинности логической функции
Определяют количество строк: кол-во строк = $2^n + 1$ (для строки заголовка), $n$ – количество простых выражений. Например, для функций двух переменных существует $2^2 = 4$ комбинации наборов значений переменных, для функций трех переменных – $2^3 = 8$ и т.д.
Определяют количество столбцов: кол-во столбцов = кол-во переменных + кол-во логических операций. При определении количества логических операций учитывают также порядок их выполнения.
Заполняют столбцы результатами выполнения логических операций в определенной последовательности, учитывая таблицы истинности основных логических операций.
Готовые работы на аналогичную тему

Составить таблицу истинности логического выражения $D=\bar \vee (B \vee C)$.
Решение:
Определим количество строк:
Количество простых выражений – $n=3$, значит
кол-во строк = $2^3 + 1=9$.
Определим количество столбцов:
Количество переменных – $3$.
Количество логических операций и их последовательность:
Кол-во столбцов = $3 + 3=6$.
Заполним таблицу, учитывая таблицы истинности логических операций.

По данному логическому выражению построить таблицу истинности:
Решение:
Определим количество строк:
Количество простых выражений – $n=3$, значит
кол-во строк = $2^3 + 1=9$.
Определим количество столбцов:
Количество переменных – $3$.
Количество логических операций и их последовательность:
- отрицание ($\bar$);
- дизъюнкция, т.к. она находится в скобках ($A \vee B$);
- конъюнкция ($(A\vee B)\bigwedge \overline$);
- отрицание, которое обозначим $F_1$ ($\overline<(A\vee B)\bigwedge \overline>$);
- дизъюнкция ($A \vee C$);
- конъюнкция ($(A\vee C)\bigwedge B$);
- отрицание, которое обозначим $F_2$ ($\overline<(A\vee C)\bigwedge B>$);
Кол-во столбцов = $3 + 8 = 11$.
Заполним таблицу, учитывая таблицу истинности логических операций.

Алгоритм построения логической функции по ее таблице истинности
- Выделяют в таблице истинности строки со значением функции, равным $1$.
- Выписывают искомую формулу как дизъюнкцию нескольких логических выражений. Количество этих выражений равно количеству выделенных строк.
- Каждое логическое выражение в этой дизъюнкции записать как конъюнкцию аргументов функции.
- В случае, когда значение какого-то из аргументов функции в соответствующей строке таблицы принимает значение $0$, то этот аргумент записать в виде его отрицания.
По данной таблице истинности некоторой логической функции $Y(A,B)$ cоставить соответствующую логическую функцию.

Решение:
- Значение функции равно $1$ в $1$-й и $3$-й строках таблицы.
- Поскольку имеем $2$ строки, получим дизъюнкцию двух элементов:
Таблица истинности — это таблица, описывающая логическую функцию, а именно отражающую все значения функции при всех возможных значениях её аргументов.
Таблица истинности необходима для совершения логических операций. Она включает в себя n+1 столбцы и 2 n строки, где n - число используемых переменных. В первых n столбцах представлены разные значения аргументов функции, а в n+1 столбце представлены значения функции, которые она принимает на данном наборе аргументов.
Набором называется совокупность значений переменных. А = 0, В = 1. В случае, когда количество переменных n, число различных наборов будет равно 2 N . Например, для трех переменных число разных наборов будет равно 2 3 = 8.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Для создания таблиц истинности используются обозначения логических значений 0 (ложь) и 1 (истина).
Можно встретить вариацию таблицы, в которой число столбцов равно n + число используемых логических операций. В подобной таблице в первые n столбцы, так же как и в первом варианте, вписаны наборы аргументов, а остальные столбцы заполнены значениями подфункций, которые входят в запись функции. Благодаря этим промежуточным вычислениям, упрощается расчет конечного значения функции.
Применение таблиц истинности чаще всего встречается в булевой алгебре и в цифровой электронной технике для описания работы логических схем.
Логические операции
Логические операции — построение из одного или нескольких высказываний нового высказывания.
Результатом может являться не только образование нового высказывания, но и изменение содержания или объема уже данных высказываний. В случае логической операции истинность значения нового высказывания всецело определяется истинностью значения исходных высказываний.
К логическим операциям относятся конъюнкция, дизъюнкция, импликация, разделительная дизъюнкция, эквиваленция, антиконъюнкция, антидизъюнкция.
Логические выражения
Их можно разделить на два типа:
-
выражения, использующие операции сравнения и принимающие логические значения. Например, выражение a Определение
Инверсия или логическое отрицание — это логическая операция, при выполнении которой из данного высказывания получается новое высказывание. Это высказывание является отрицанием исходного высказывания.
Унарной в данном случае называется операция, которая используется относительно одной величины.
Конъюнкция
Конъюнкция может быть истинной только в том случае, если оба высказывания истинны. Например, A ∧ B, если A = ложь, а B = истина, является ложным.
Дизъюнкция
Логическое высказывание будет истинным, если истинно хотя бы одно из условий. Например, A ∨ B истинно, даже если А = истина, а В = ложь. Высказывание будет ложным только в том случае, если ложны и А, и В.
Правила составления таблицы истинности
Таблицу истинности можно построить для любого логического выражения. В этой таблице будут отражены все значения, которые принимает выражение при всех наборах значений входящих в него переменных.
Строить таблицы истинности необходимо по следующему алгоритму:
- Вычислить число переменных в выражении (n).
- Вычислить общее количество логических операций в выражении.
- Определить последовательность, в которой будут выполняться логические операции.
- Установить количество столбцов в таблице — количество переменных и количество операций.
- Внести в шапку таблицы переменные и операции, соблюдая последовательность, определенную в пункте 3.
- Высчитать количество строк в таблице, используя формулу m = 2 n
- Занести в таблицу наборы входных переменных. Они представляют собой целый ряд n-разрядных двоичных чисел от 0 до 2 n −1.
- Заполнить таблицу, совершая логические операции.
Примеры построения таблицы истинности
Задача
Построим таблицу истинности и решим выражение \( F = (A \vee B) \wedge (¬A \vee ¬B)\) . Будем пользоваться приведенным выше алгоритмом.
- Число переменных в выражении n = 2.
- Общее количество логических операций в выражении — 5.
- Последовательность выполнения логических операций — 1, 5, 2, 4, 3.
- Количество столбцов — 7. Логические переменные (А и В) + логические операции \(\vee\) , \(\wedge\) , \(¬\) , \(\vee\) , \(¬\) = 2 +5 = 7.
- Количество строк — 5, исходя из m =2 n , таким образом 2 2 = 4, 4+1 (строка заголовков столбцов) = 5.
- Заполним таблицу.
Решение
| А | В | \(А \vee В\) | ¬А | ¬В | \(¬А \vee ¬В\) | \((A \vee B) \wedge (¬A \vee ¬B)\) |
| 0 | 0 | 0 | 1 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 |
После заполнения таблицы, ответ будет выглядеть следующим образом:
F = 0 при A = B = 0 и A = B = 1
Задача
Построим еще одну таблицу истинности и решим выражение \(F = X \vee Y \wedge ¬Z\)
Читайте также:

