Обновлено: 17.05.2024

Определение и характеристика главных свойств тригонометрических и обратных тригонометрических функций. Изучение основных типов тригонометрических неравенств. Рассмотрение формул, упрощающих выражения и содержащих обратные тригонометрические функции.

Рубрика	Математика
Вид	контрольная работа
Язык	русский
Дата добавления	15.01.2017
Размер файла	332,0 K

Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.

1. Основные понятия и формулы тригонометрии

2. Изучение основных типов тригонометрических уравнений и методы их решения

3. Изучение основных типов тригонометрических неравенств и методы их решения

3.1 Решение простейших тригонометрических неравенств

3.2 Решение тригонометрических неравенств с помощью единичной окружности

3.3 Решение тригонометрических неравенств графическим методом

Введение

Специфика математики, ее роль в современных условиях позволяет через математику, через ее использование показать различные стороны многих современных процессов.

Значительную часть школьного курса математики составляет материал, связанный с уравнениями и неравенствами. Это объясняется тем, что уравнения и неравенства широко используются в различных разделах математики, в решении важных прикладных задач.

Данная работа посвящена методам решения тригонометрических уравнений и неравенств.

В первом параграфе приведены основные теоретические сведения:

определение и свойства тригонометрических и обратных тригонометрических функций; таблица значений тригонометрических функций для некоторых аргументов; выражение тригонометрических функций через другие тригонометрических функции, что очень важно для преобразования тригонометрических выражений, в особенности содержащих обратные тригонометрические функции; кроме основных тригонометрических формул, хорошо известных из школьного курса, приведены формулы упрощающие выражения, содержащие обратные тригонометрические функции.

Во втором параграфе изложены основные методы решения тригонометрических уравнений. Рассмотрены решение элементарных тригонометрических уравнений, метод разложения на множители, методы сведения тригонометрических уравнений к алгебраическим.

В третьем параграфе рассматриваются тригонометрические неравенства. Подробно рассмотрены методы решения элементарных тригонометрических неравенств, как на единичной окружности, так и графическим методом.

1. Основные понятия и формулы тригонометрии

В тригонометрии угол рассматривается как мера вращения, при котором один луч, вращаясь вокруг вершины угла, переходит в положение другого луча. При этом первый луч называют начальной стороной угла, а конечное положение второго (подвижного) луча называют конечной стороной угла. тригонометрический неравенство формула

Угол считается положительным, если переход от его начальной стороны к конечной совершается вращением подвижного луча против часовой стрелки, и отрицательным, если такой переход совершается вращением по часовой стрелке.

Единичный круг - круг с центром в начале координат и радиусом, равным по длине единице. Окружность этого круга называется единичной окружностью.

Координатные оси делят единичный круг и его окружность на четыре равные части, которые называются четвертями, или квадрантами.

Синус - отношение ординаты конца подвижного радиуса к длине этого радиуса.

Косинус - отношение абсциссы конца подвижного радиуса к длине этого радиуса.

Тангенс - отношение ординаты конца подвижного радиуса к его абсциссе.

Котангенс - отношение абсциссы конца подвижного радиуса к его ординате.

Секанс - отношение длины подвижного радиуса к абсциссе его конца.

Косеканс - отношение длины подвижного радиуса к ординате его конца.

Линия тангенсов - касательная к единичной окружности в конце горизонтального диаметра.

Линия котангенсов - касательная к единичной окружности в конце вертикального диаметра.

Синус и косинус угла равны соответственно ординате и абсциссе конца подвижного радиуса единичной окружности.

Если продолжить единичный радиус до пересечения с линией тангенсов, то тангенс угла равен ординате соответствующей точки на линии котангенсов.

Если продолжить единичный радиус до пересечения с линией котангенсов, то котангенс угла равен абсциссе соответствующей точки на линии котангенсов.

Основные тригонометрические тождества:

Тождественные преобразования тригонометрических выражений.

Функция называется четной, если значение не изменяется при замене на , т.е. функция ) называется четной, если .

Функции , , - четные функции, а , , - нечетные.

Теоремы сложения позволяют, зная значения тригонометрических функций двух аргументов и , вычислять значения тригонометрических функций от суммы и разности этих аргументов.

Формулы, при помощи которых тригонометрические функции произвольного угла можно выразить через тригонометрические функции острого угла, называются формулами приведения.

Формулы удвоения и деления аргумента.

Формулы преобразования произведения тригонометрических функций в сумму

2. Изучение основных типов тригонометрических уравнений и методы их решения

Тригонометрические уравнения - обязательная тема любого экзамена по математике. Основные приемы их решения - замена переменной и разложение на множители. Для успешного решения тригонометрических уравнений нужно хорошо знать тригонометрические формулы, причем не только основные, но и дополнительные (преобразование суммы тригонометрических функций в произведение и произведения в сумму, формулы понижения степени и другие).

Разумеется, должны четко знать стандартные формулы корней простейших тригонометрических уравнений (полезно помнить или уметь получать с помощью тригонометрической окружности упрощенные формулы для корней уравнений

Определение. Тригонометрическим уравнением называется уравнение, содержащее переменную под знаком тригонометрических функций.

Определение. Простейшие тригонометрические уравнения - это уравнения вида

В таких уравнениях переменная находится под знаком тригонометрической функции, -- данное число.

При решении тригонометрических уравнений все задачи сводятся к тому, чтобы привести к такому виду, чтобы слева стояла элементарная тригонометрическая функция, а справа - число. После того, как это будет достигнуто, следует найти значение аргумента функции, используя одну из основных формул выражения аргумента через обратные тригонометрические функции.

Методы решения тригонометрических уравнений.

1) Алгебраический метод.

Этот метод нам хорошо известен из алгебры (метод замены переменной и подстановки).

Пример. Решить уравнение

Решение. Используя формулы приведения, имеем

откуда следует два случая:

2) Разложение на множители.

Приводим уравнение к виду и представляем левую часть уравнения в виде произведения ). Тогда данное уравнение приводится к совокупности уравнений: . Следует помнить, что эта совокупность не всегда равносильна исходному уравнению и что здесь надо руководствоваться правилом: произведение равно нулю тогда и только тогда, когда один из множителей равен нулю, а все остальные при этом имеют смысл.

Этот метод рассмотрим на примере.

Пример. Решить уравнение .

Решение. Перенесём все члены уравнения влево

преобразуем и разложим на множители выражение в левой части уравнения:

3) Приведение к однородному уравнению.

Уравнение называется однородным относительно и , если все его члены одной и той же степени относительно и одного и того же угла. Чтобы решить однородное уравнение, надо:

а) перенести все его члены в левую часть;

б) вынести все общие множители за скобки;

в) приравнять все множители и скобки нулю;

г) скобки, приравненные нулю, дают однородное уравнение меньшей степени, которое следует разделить на ( или ) в старшей степени;

д) решить полученное алгебраическое уравнение относительно .

Пример. Решить уравнение: .

корни этого уравнения: , отсюда

3.1 Решение простейших тригонометрических неравенств

Большинство авторов современных учебников по математике предлагают начать рассмотрение данной темы с решения простейших тригонометрических неравенств. Принцип решения простейших тригонометрических неравенств основан на знаниях и умениях определять на тригонометрической окружности значения не только основных тригонометрических углов, но и других значений.

Между тем, решение неравенств вида можно осуществлять следующим образом: сначала находим какой-нибудь промежуток , на котором выполняется данное неравенство, а затем записываем окончательный ответ, добавив к концам найденного промежутка число кратное периоду синуса или косинуса: . При этом значение находится легко, т.к. или . Поиск же значения опирается на интуицию учащихся, их умение заметить равенство дуг или отрезков, воспользовавшись симметрией отдельных частей графика синуса или косинуса. А это довольно большому числу учащихся иногда оказывается не под силу. В целях преодоления отмеченных трудностей в учебниках в последние годы применялся разный подход к решению простейших тригонометрических неравенств, но улучшения в результатах обучения это не давало.

Мы на протяжении ряда лет для нахождения решения тригонометрических неравенств довольно успешно применяем формулы корней соответствующих уравнений.

Изучение данной темы осуществляем таким образом:

1. Строим графики и , считая, что .

Затем записываем уравнение и его решение . Придавая , находим три корня составленного уравнения: . Значения являются абсциссами трёх последовательных точек пересечения графиков и . Очевидно, что всегда на интервале () выполняется неравенство , а на интервале - неравенство .

Добавив к концам этих промежутков число, кратное периоду синуса, в первом случае получим решение неравенства в виде: ; а во втором случае - решение неравенства в виде: .

2. Далее проводим аналогичные рассуждения для косинуса

Только в отличие от синуса из формулы , являющейся решением уравнения , при получаем два корня , а третий корень при в виде . И опять являются тремя последовательными абсциссами точек пересечения графиков и . В интервале выполняется неравенство , в интервале - неравенство .

Теперь нетрудно записать решения неравенств и . В первом случае получим: ; а во втором: .

Подведём итог. Чтобы решить неравенство или , надо составить соответствующее уравнение и решить его. Из полученной формулы найти корни и , и записать ответ неравенства в виде: .

При решении неравенств , из формулы корней соответствующего уравнения находим корни и , и записываем ответ неравенства в виде: .

Данный приём позволяет научить решать тригонометрические неравенства всех учащихся, т.к. этот приём полностью опирается на умения, которыми учащиеся владеют прочно. Это умения решать простейшие и находить значение переменной по формуле. Кроме того, становится совершенно необязательным тщательное прорешивание под руководством учителя большого количества упражнений для того, чтобы продемонстрировать всевозможные приёмы рассуждений в зависимости от знака неравенства, значения модуля числа a и его знака. Да и сам процесс решения неравенства становится кратким и, что очень важно, единообразным.

Ещё одним из преимуществ данного способа является то, что он позволяет легко решать неравенства даже в том случае, когда правая часть не является табличным значением синуса или косинуса.

Продемонстрируем это на конкретном примере. Пусть требуется решить неравенство . Составим соответствующее уравнение и решим его: .

Найдём значения и .

Записываем окончательный ответ данного неравенства:

В рассмотренном примере решения простейших тригонометрических неравенств недостаток может быть только один - наличие определенной доли формализма. Но если всё оценивать только с этих позиций, то тогда можно будет обвинить в формализме и формулы корней квадратного уравнения, и всех формул решения тригонометрических уравнений, и многое другое.

Предложенный метод хоть и занимает достойное место в формировании умений и навыков решения тригонометрических неравенств, но нельзя и преуменьшать важность и особенности других методов решения тригонометрических неравенств.

3.2 Решение тригонометрических неравенств с помощью единичной окружности

При решении тригонометрических неравенств вида , где - одна из тригонометрических функций, удобно использовать тригонометрическую окружность для того, чтобы наиболее наглядно представить решения неравенства и записать ответ. Основным методом решения тригонометрических неравенств является сведение их к простейшим неравенствам типа . Разберём на примере, как решать такие неравенства.

Пример. Решите неравенство .

Решение. Нарисуем тригонометрическую окружность и отметим на ней точки, для которых ордината превосходит .

Для решением данного неравенства будут . Ясно также, что если некоторое число будет отличаться от какого-нибудь числа из указанного интервала на , то также будет не меньше . Следовательно, к концам найденного отрезка решения нужно просто добавить . Окончательно, получаем, что решениями исходного неравенства будут все .

Для решения неравенств с тангенсом и котангенсом полезно понятие о линии тангенсов и котангенсов. Таковыми являются прямые и

соответственно, касающиеся тригонометрической окружности.

Легко заметить, что если построить луч с началом в начале координат, составляющий угол с положительным направлением оси абсцисс, то длина отрезка от точки до точки пересечения этого луча с линией тангенсов в точности равна тангенсу угла, который составляет этот луч с осью абсцисс. Аналогичное наблюдение имеет место и для котангенса.

3.3 Решение тригонометрических неравенств графическим методом

Заметим, что если - периодическая функция, то для решения неравенства необходимо найти его решения на отрезке, длина которого равна периоду функции . Все решения исходного неравенства будут состоять из найденных значений , а также всех , отличающихся от найденных на любое целое число периодов функции .

Пример. Рассмотрим решение неравенства .

Решение. Рассмотрим график функции .

и выберем из промежутка на оси значения аргумента , которым соответствуют точки графика, лежащие выше оси . Таким промежутком является интервал . Учитывая периодичность функции все решения неравенства можно записать так:

Проблема отбора корней, отсеивания лишних корней при решении тригонометрических уравнений весьма специфична и обычно оказывается более сложной, чем это имело место для уравнений алгебраических. Приведем решения уравнений, иллюстрирующие типичные случаи появления посторонних корней и методы > с ними.

Пример. Найти корни уравнения: .

Решение этого уравнения распадается на два этапа: 1) решение уравнения, получающегося из данного возведением в квадрат обеих его частей; 2) отбор тех корней, которые удовлетворяют условию . При этом заботится об условии нет необходимости. Все значения , удовлетворяющие возведенному в квадрат уравнению, этому условию удовлетворяют.

Первый шаг нас приводит к уравнению , откуда .

Теперь надо определить, при каких будет . Для этого достаточно для рассмотреть значения т. е. >, поскольку дальше значения косинуса начнут повторяться, получившиеся углы будут отличаться от уже рассмотренных на величину, кратную .

Итак, основная схема отбора корней состоит в следующем. Находится наименьший общий период всех тригонометрических функций входящих в уравнение. На этом периоде отбираются корни, а затем оставшиеся корни периодически продолжаются.

Литература

3. Шабашова О.В. Приемы отбора корней в тригонометрических уравнениях //Математика в школе. 2004. №1. С.20-24.

6. Мордкович А.Г . Алгебра и начала анализа. 10-11 кл.: Учебник для общеобразовательных учреждений. - М.: Мнемозина, 2000. - 336с.:ил.

7. Мордкович А.Г. Методические проблемы изучения тригонометрии в общеобразовательной школе // Математика в школе. 2002. №6.

Подобные документы

Углы и их измерение, тригонометрические функции острого угла. Свойства и знаки тригонометрических функций. Четные и нечетные функции. Обратные тригонометрические функции. Решение простейших тригонометрических уравнений и неравенств с помощью формул.

учебное пособие [876,9 K], добавлен 30.12.2009

История развития тригонометрии, характеристика ее основных понятий и формул. Общие вопросы, цели изучения и способы определения тригонометрических функций числового аргумента в школьном курсе. Рекомендации и методы решения тригонометрических уравнений.

курсовая работа [257,7 K], добавлен 19.10.2011

Тригонометрические уравнения и неравенства в школьном курсе математики. Анализ материала по тригонометрии в различных учебниках. Виды тригонометрических уравнений и методы их решения. Формирование навыков решения тригонометрических уравнений и неравенств.

дипломная работа [1,9 M], добавлен 06.05.2010

Элементарные тригонометрические уравнения и методы их решения. Введение вспомогательного аргумента. Схема решения тригонометрических уравнений. Преобразование и объединение групп общих решений тригонометрических уравнений. Разложение на множители.

курсовая работа [1,1 M], добавлен 21.12.2009

Характеристика тригонометрических понятий. Свойства тригонометрических функций, особенности их практического применения в электротехнике. Исследование электрических сигналов путем визуального наблюдения графика сигнала на экране с помощью осциллографа.

презентация [287,9 K], добавлен 28.05.2016

Углы и их измерение. Соответствие между углами и числовым рядом. Геометрический смысл тригонометрических функций. Свойства тригонометрических функций. Основное тригонометрическое тождество и следствия из него. Универсальная тригонометрическая подстановка.

учебное пособие [1,4 M], добавлен 18.04.2012

Частные случаи производной логарифмической функции. Производная показательной функции, экспоненты, степенной, тригонометрических функций. Производная синуса, косинуса, тангенса, котангенса, арксинуса. Производные обратных тригонометрических функций.

• Для учеников 1-11 классов и дошкольников
• Бесплатные сертификаты учителям и участникам

МБОУ Алтайская СОШ №1

Учащаяся 9 а класса

МБОУ Алтайская СОШ №1

Бабаева Галина Яковлевна,

МБОУ Алтайской СОШ №1

С. Алтайское , Алтайский район, 2019 год.

II . Основная часть

2. Как графически решить уравнение________________________стр.4

3. Какие бывают функции ?________________________________стр.4

4. Графическое решение линейного уравнения с одной переменной.стр.5

5. Решение квадратного уравнения графическим способом._____ стр6-8

8. Решение линейных неравенств графическим способом стр 14

IV . Список литературы______________________________________стр.16

I .Введение.

Цель моей работы – изложить графический метод решения уравнений и неравенств, который дает возможность определить корни или доказать ,что уравнение корней не имеет ( или решением неравенства является пустое множество).

Актуальность темы : графический метод, опирающийся на знания элементарных функций, удобно применять при решении задач на нахождение числа корней и на нахождение корней уравнений.

Изучение поведения функций и построение их графиков является важным разделом математики. Свободное владение техникой построения графиков часто помогает решать многие задачи и порой является единственным средством решения. Кроме того, умение строить графики функций представляет большой самостоятельный интерес. В данной исследовательской работе я показала как наиболее удобным способом преобразовывать уравнения . чтобы сводить к построению элементарных функций.

Часто построение графиков связано с исследованием поведения функций. Однако необходимость построения графиков не ограничивается только этим. В ряде случаев графики облегчают нахождение решений уравнений и неравенств, сокращая и упрощая аналитические выкладки, и часто при этом являются единственным методом решения таких задач. Данный метод может использоваться не только для одиночных уравнений, но и для их систем, а также неравенств

II . Основная часть

1.Основные понятия.

Уравнение – выражение, содержащее переменную.

Решить уравнение – это значит найти все его корни, или доказать, что их нет.

Корень уравнения – это число, при подстановке которого в уравнение получается верное числовое равенство.

График функции – это множество всех точек координатной плоскости, абсциссы которых равны значениям аргументов, а ординаты – соответствующим значениям функции.

Решение уравнений графическим способом позволяет найти точное или приближенное значение корней, позволяет найти количество корней уравнения.

При построении графиков и решении уравнений используются свойства функции, поэтому метод чаще называют функционально-графическим. Графиком функции y = f(x) называется множество всех точек координатной плоскости.

Заметим , что так как функция f сопоставляет каждому x D(f) одно число f(x) , то график функции f пересекается любой прямой, параллельной оси ординат, не более, чем в одной точке. И наоборот: всякое непустое множество точек плоскости, имеющее со всякой прямой, параллельной оси ординат, не более одной общей точки, является графиком некоторой функции.

Не всякое множество точек координатной плоскости является графиком какой-либо функции. Например, множество точек окружности не может быть графиком функции, поскольку значению абсциссы внутри окружности, соответствует два значения ординаты.

В общем случае уравнение с одной переменой х можно записать в виде f(x)=g(x),где f(x) и g(x) - некоторые функции. Функция f(x) является левой частью , а g(x) - правой частью уравнения.

Тогда для решения уравнения необходимо построить в одной системе координат графики функций f(x) и g(x). Абсциссы точек пересечения будут являться решениями данного уравнения.

Использование монотонности функций при решении уравнений: если функция строго возрастает, а функция строго убывает на некотором множестве, то графики этих функций имеют не более одной точки пересечения, а уравнение на этом множестве имеет не более одного решения. Поэтому, чтобы решить такие уравнения можно подобрать (если это удается) число, которое является их корнем.

2. Как графически решить уравнение.

Иногда уравнения решают графическим способом. Для этого надо преобразовать уравнение так (если оно уже не представлено в преобразованном виде), чтобы слева и справа от знака равенства стояли выражения, для которых легко можно нарисовать графики функций. Графическим решением уравнения являются абсциссы точек пересечения графиков построенных функций. Графики могут пересекаться в нескольких точках, в одной точке, вообще не пересекаться. Отсюда следует, что уравнение может иметь несколько корней, или один корень, или вообще их не иметь.

3. Какие бывают функции .

Линейная функция задаётся уравнением у = k*x+ b , где k и b – некоторые числа. Графиком этой функции является прямая. Для построения прямой достаточно в таблице значений взять только две точки. Это вытекает из аксиомы планиметрии

Функция обратной пропорциональности у =k/x , где. График этой функции называется гиперболой.

Функция (х– a)^2+ (у – b)^2 = r^2 , где а , b и r – некоторые числа. Это окружность радиуса r с центром в т. А ( а , b ).

Квадратичная функция y = a *х 2 + b*x+ c , где а, b, с – некоторые числа и

а не равно 0. Графиком этой функции является парабола.

Графики линейных функций, содержащих выражение под знаком модуля.

Для построения графиков функций, содержащих выражение под знаком модуля, сначала находят корни выражений, стоящих под знаком модуля. Эти корни разбивают числовую прямую на промежутки. График строят в каждом промежутке отдельно.

В простейшем случает, когда только одно выражение стоит под знаком модуля и нет слагаемых без знака модуля, можно построить график функций,

опустив знак модуля, а затем часть графика, расположенного в области отрицательных значений y , отобразить симметрично оси ОХ.

Элементарная функций, содержащая модуль :

4. Графическое решение линейного уравнения с одной переменной.

Как мы уже знаем, графиком линейного уравнения является прямая линия, отсюда и название данного вида. Линейные уравнения достаточно легко решать алгебраическим путем – все неизвестные переносим в одну сторону уравнения, все, что нам известно – в другую и уравнение решено. Мы нашли корень .А я покажу , как это сделать графическим способом.

Задание . Решить графическим способом уравнение : 2 x − 10 = 2

1)Перенесем слагаемые следующим образом: 2 x = 12.

2) Построим графики функций: y=2x и y=12.

Но можно решать и по-другому.

Для рассмотрения альтернативного решения вернемся к нашему уравнению:

Построим графики функций: y=2 x − 10 y =2

5. Решение квадратного уравнения графическим способом.

Задание. Решить уравнение : х 2 + 2 x − 8 = 0

Для этого преобразуем уравнение к виду: х 2 =-2x+8 . Построим графики функций: у = -2x+8 и у = х 2

Получим точки пересечения графиков данных функций.

В ответ запишем абсциссы этих точек : x = -4 и x =2.

Данное уравнение можно решить , переписав уравнение следующим образом: x^2 – 8 = -2x

Тогда будем строить графики функций: y = x^2 – 8 и y = -2x.

А также уравнение можно решить , переписав следующим образом:

Тогда будем строить графики следующих функций : y = x^2 + 2x и y = 8 .

При этом абсциссы точек пересечения графиков будут одинаковые :

Задание. Решить уравнение: x² – 2x = 0

Перепишем уравнение в виде : x² = 2x

Построим графики функций y = x² и y = 2 и найдем точки их пересечения :

Задание. Решить уравнение: х 2 +2=0

Преобразуем так: х 2 = -2

Построим графики функций: у=-2 и у= х 2

Графики функций не пересекаются ,поэтому уравнение решений не имеет.

Ответ : решений нет.

6. Графическое решение смешанных уравнений.

Задание. Решить уравнение: 3/х +2 =х

1)Перенесем слагаемые таким образом: 3/ х = х-2

2) Построим графики функций от каждой части уравнения.

Найдем координаты точек пересечения графиков данных функций.

Из построения видно, что графики функций пересекаются в точках с координатами : (3;1) и(-1;-3).

Задание. Решить уравнение: 2 х^3 – x - 1=0

Перепишем его так : 2 х 3 = x + 1

Построим графики функций от левой и правой части уравнения:

у= 2 х 3 (графиком этой функции является кубическая парабола) и график от правой части уравнения :у=х+1

Из построения видно, что абсцисса точки пересечения является х=1. значит, в ответ нужно записать: х=1

Решим графическим способом такое уравнение : х 3 =8.

Строим графики функций: у = х 3 и у=8., затем найдем абсциссу точки пересечения графиков этих функций.

Задание. Решить уравнение: √x – 0.5x = 0

Перепишем так: √x = 0.5x

Построим графики функций: у= 0.5x и у = √x

Как видно из построения, графики функций пересекаются в двух точках:

Нас интересует только координата x.

Значит уравнение √x – 0.5x = 0 имеет два корня: x ₁ = 0 и x ₂ = 4.

7. Решение квадратных неравенств графическим способом.

Способ , который нам хорошо известен при изучении данной темы по учебнику.

Я же предлагаю переписать неравенство следующим образом : х^2-4>3х.

Построим графики функций от левой и правой частей неравенства.

Выделим ту часть, где график от левой части выше графика от правой части.

На мой взгляд такое решение более красивое , интересное и более понятное.

8. Решение линейных неравенств и систем неравенств графическим способом.

,

Называют ся линейными неравенствами .

График линейного или квадратного неравенства строится так же, как строится график любой функции (уравнения).

Разница заключается в том, что неравенство подразумевает наличие множества решений, поэтому график неравенства представляет собой не просто точку на числовой прямой или линию на координатной плоскости.

С помощью математических операций и знака неравенства можно определить множество решений неравенства

Вообще графический способ решения неравенств с одной переменной применяется не только для решения квадратных неравенств, но и неравенств других видов.

Суть графического способа решения неравенств следующая:

рассматривают функции y = f(x) и y = g(x) , которые соответствуют левой и правой частям неравенства, строят их графики в одной прямоугольной системе координат и выясняют, на каких промежутках график одной из них располагается ниже или выше другого.

Те промежутки, на которых график функции у = f (х) выше графика функции y = g(х) являются решениями неравенства f(x)>g(x) ;

график функции y = f(х) не ниже графика функции y = g(x) являются решениями неравенства f(x) ≥ g(x) ;

график функции у = f (х) ниже графика функции y = g(х) являются решениями неравенства f(x) ;

график функции y = f(х) не выше графика функции y = g(х) являются решениями неравенства f(x) ≤ g(x) .

Также скажем, что абсциссы точек пересечения графиков функций y = f(x) и y = g(x) , являются решениями уравнения f(x) = g(x) .

III . Заключение.

Мы рассмотрели графический метод решения уравнений и квадратных неравенств; рассмотрели конкретные примеры, при решении которых использовали некоторые свойства функций.

Иногда при графическом решении некоторых уравнений и неравенств корни определяются только приближённо в силу того, что невозможно с высокой точностью построить график функции, измерить абсциссы или ординаты точек пересечения графика с осями координат или с другими графиками. Тем не менее, той точности, которую обеспечивает графический метод, бывает вполне достаточно для практических нужд.

Построение графиков основывается на знании основных элементарных функций, и на основные методы построения графиков функций. В работе представлено достаточное количество примеров, раскрывающих графический метод решения линейных и квадратных уравнений и неравенств, который доступен для понимания .

Работа может быть использована для углубления и расширения знаний в области построения графиков функций и использовании графического метода при решении некоторых видов уравнений и неравенств. Теорию можно использовать так же при подготовки к экзаменам , к олимпиадам.

Это и закрепление изученных свойств функций, и прекрасная демонстрация их применения на практике.

В старших классах я буду ещё знакомиться с другими функциями , с другими уравнениями и неравенствами и м не интересно будет продолжить свой проект.

* Данная работа не является научным трудом, не является выпускной квалификационной работой и представляет собой результат обработки, структурирования и форматирования собранной информации, предназначенной для использования в качестве источника материала при самостоятельной подготовки учебных работ.

Ставропольский Государственный Университет

РЕФЕРАТ

работу выполнил:

IV курса, Физ-Мат Факультета,

отделения МИИТ, гр. ”Б”

Неботов Виталий Дмитриевич

Ставрополь 1997 г.

1. Вступительное слово. 3

2. Этапы “большого пути”. 3

3. Тригонометрические отношения. 3

4. Тригонометрические функции. 3

5. Тригонометрические уравнения. 3

6. Тригонометрические неравенства. 3

7. Способы решения тригонометрических неравенств. 4

8. В помощь начинающему . 5

10. Список использованной литературы. 6

Решение тригонометрических неравенств стоит в одном ряду с такими важными темами, как решение числовых неравенств и решение систем неравенств с одной переменной. Исторически сложилось, что тригонометрическим уравнениям и неравенствам уделялось особое место в школьном курсе. Еще греки, на заре человечества, считали тригонометрию важнейшей из наук, ибо геометрия - царица математики, а тригонометрия - царица геометрии. Поэтому и мы, не оспаривая древних греков, будем считать тригонометрию одним из важнейших разделов школьного курса, да и всей математической науки в целом.

С чего же начинается обучение решению тригонометрических неравенств в школе? Естественно, с самих тригонометрических функций. Сначала даются сами отношения sin x, cos x, tg x и ctg x. Делается это на конкретных примерах рассматриваемых треугольников. Затем делается важный переход от синуса и косинуса в прямоугольном треугольнике к этим же отношениям, но уже в произвольном угле. Sin и cos освобождаются от конкретной геометрической привязки и эти понятия становятся шире.

Следующим этапом введения понятий sin x, cos x, tg x и ctg x является рассмотрение функциональных зависимостей или попросту функций y = sin x, y = cos x, y = tg x и y = ctg x соответственно. На этом этапе даются все основные свойства этих функций, рассматриваются области определения и значений, промежутки знакопостоянства, и главное - графики этих функций. Анализ функции нельзя считать полным, так как еще не усвоен и не применялся аппарат дифференцирования, но для решений тригонометрических неравенств почва уже подготовлена и ребята хорошо “вооружены” теоретическими знаниями.

Наконец последний подготовительный этап “большого пути” - решение тригонометрических уравнений. Здесь отрабатываются последние нюансы, ребенок учится оперировать сложными тригонометрическими конструкциями, но главное, именно сейчас даются основные тригонометрические тождества и производные от них. Помощь этого тригонометрического аппарата трудно переоценить. Знаниями полученными здесь и сейчас ученики смогут пользоваться всю оставшуюся жизнь. Мощь блока тригонометрических тождеств поистине потрясает, так как с его помощью управляться с громоздкими, “трехэтажными” тригонометрическими выражениями становится также просто, как и с алюминиевой вилкой.

И только теперь, хорошо освоив все предыдущие разделы ученики подходят к нашей теме, а именно решение тригонометрических неравенств. Естественно начинают решение таких неравенств с самых простейших: sin x > a, sin x a, cos x a, tg x 2 + ОУ 2 = R 2 . Таким образом, подставив синус и косинус получим: sin 2 x + cos 2 x = 1. Вот так мы и вышли на основное тригонометрическое тождество. Именно поэтому тригонометрический круг единичного радиуса.

Как я уже сказал, мы, с помощью тригонометрических тождеств, приводим неравенство к простейшему виду, а затем решаем его используя тригонометрический круг или график. Для успешного решения необходимо также знать следующее:

Примеры решения простейших тригонометрических неравенств

Простейшими тригонометрическими неравенствами называются неравенства вида

где – один из знаков , .

Вы должны прежде, конечно, хорошо ориентироваться в тригонометрическом круге и уметь решать простейшие тригонометрические уравнения (часть I, часть II).

Кстати, умение решать тригонометрические неравенства может пригодиться, например, в заданиях №11 ЕГЭ по математике.

Сначала мы рассмотрим простейшие тригонометрические неравенства с синусом и косинусом . Во второй части статьи – с тангенсом, котангенсом.

Пример 1.

Отмечаем на оси косинусов

Все значения , меньшие – левее точки на оси косинусов.

Отмечаем все точки (дугу, точнее – серию дуг) тригонометрического круга, косинус которых будет меньше

Полученную дугу мы проходим против часовой стрелки (!) , то есть от точки до .

Обратите внимание, многие, назвав первую точку вместо второй точки указывают точку , что неверно!

Становится видно, что неравенству удовлетворяют следующие значения

Вот так выглядит графическое решение неравенства не на тригонометрическом круге, а в прямоугольной системе координат:

Пример 2.

Отмечаем на оси косинусов

Все значения , большие или равные – правее точки , включая саму точку.

Тогда выделенные красной дугой аргументы отвечают тому условию, что .

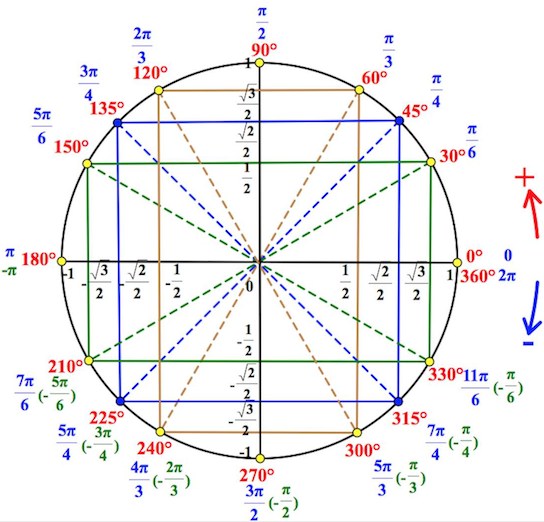
Пример 3.

Отмечаем на оси синусов

Все значения , большие или равные – выше точки , включая саму точку.

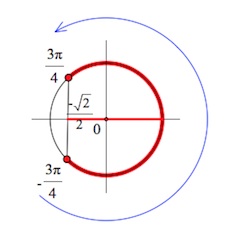
Пример 4.

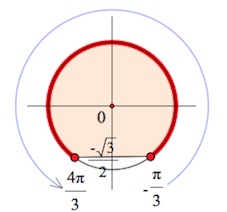
Пример 5.

Неравенство равносильно уравнению , так как область значений функции –

Пример 6.

Действия – аналогичны применяемым в примерах выше. Но дело мы имеем не с табличным значением синуса.

Здесь, конечно, нужно знать определение арксинуса.

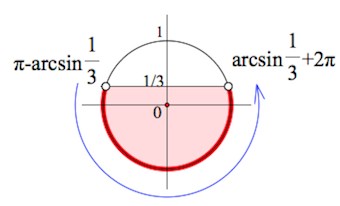
Если не очень понятно, загляните сюда –>+ показать

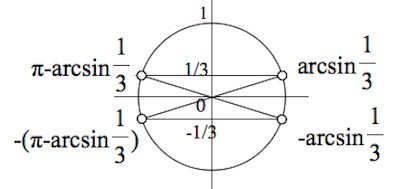
Согласны с таким вариантом (одним из) названия углов, соответствующих тому, что синус в них равен

А теперь мы должны позаботиться о том, чтобы правый конец промежутка, являющего собой решение неравенства, был бы больше левого конца.

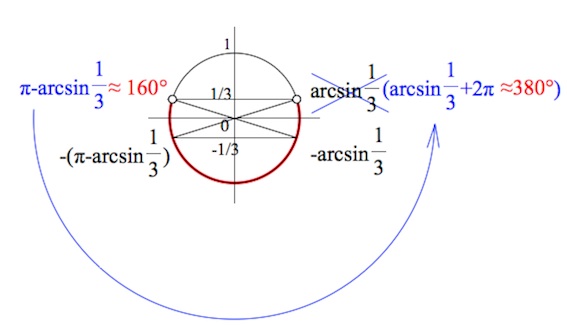
Тренируемся в решении простейших тригонометрических неравенств

Имейте ввиду , решения (ответы) к одному и тому же неравенству могут выглядеть по-разному, неся один и тот же смысл собою. Например, в задании 2 ответ можно было записать и так:

Читайте также:

  
• Битва при каннах по ливию и полибию доклад
  
• Доклад по орксэ 4 класса молитва буддистов
  
• Доклад на тему толерантность педагога
  
• Благодарность за доклад на конференции
  
• Принципы организации рекламных агентств доклад