Доклад по теме неевклидова геометрия

Обновлено: 05.07.2024

Статья написана в легком развлекательном стиле. И попытки разобраться в каких-то математических определениях могут вызвать некоторый интерес.

Правила в природе есть, обязательно и непреложно, хоть у песчинки, хоть у капли воды, а человек только правила обнаруживает и их осмысливает. Причем, поиски решений многовариантны, как и сама Природа и пути развития. Да Вы и сам в конце статьи это признаете.
Поэтому, два плюс три будет равно пяти - это следствие действий законов природы, по которым функционируют мозг, органы чувств и симпатическая система человека. Опять же, если не понимать смысла почему умножение выполняется в первую очередь, то зачем вообще браться за эту тему? Еще и интегрирование гении придумали для простоты применения в хозяйственной деятельности.
Вот чего в Природе точно нет, так это прямых линий.

Странно, чем четырехмерное пространство имеет бОльшую ограниченность, чем трехмерное?

Опять же, чтобы, как вы выразились, перейти к реальному положению вещей в природе до построения точки в плоской математической модели, мы сначала определяем пространство, которое хотим изучать. Точка - это уже объект. И эта точка как объект описывается как минимум одной функцией. Если это сложный объект, то точка имеет очень много функций. Но математически она может лежать как в двухмерном изображении, так и в любом многомерном изображении. Смотря какое пространство, какой процесс, среду или объект вы рассматриваете. Проведенная через точку прямая - это тоже функция. Как "считает земная логика" - это исключительно субъективное восприятие. Главное, что для человека существует по его интеллектуальной природе определенные взаимосвязи в познании от простого к сложному. Интеллект делится условно по качеству: 1. кристаллизующийся из накопленного опыта и навыков, отвечает за извлечение знаний и применение их в привычных условиях от частного - к общему, где не требуется включения подвижного интеллекта, основывается на вербальных процессах; 2. подвижный отвечает за построение сложных образных конструктов и раскрытие причинно-следственных связей, дедуктивное мышление от общего - к частному, оперирование с массивами информации.

/Опять же, если не понимать смысла почему умножение выполняется в первую очередь, то зачем вообще браться за эту тему?/
Опять же, если предъявляете непонимание по какому-то вопросу, и не приводите оснований, то зачем вообще спрашивать?
/Странно, чем четырехмерное пространство имеет бОльшую ограниченность, чем трехмерное?/
Это где Вы нашли у меня такое?

Роман, Вы же пишете: ". бОльшая ограниченность всегда получается зависимой от меньшей. Т.е., сначала идёт более многомерное пространство, а затем менее многомерное. " Поэтому, я интересуюсь аргументами из вашего залючения: "чем четырехмерное пространство имеет бОльшую ограниченность, чем трехмерное?

Большая ограниченность зависима от меньшей – значит то, что больше ограничено, зависимо от того, что ограничено меньше. 3хмерка больше ограничена, значит, она зависима от того, что ограничено меньше – 4хмерки. Не наоборот.

Портал Проза.ру предоставляет авторам возможность свободной публикации своих литературных произведений в сети Интернет на основании пользовательского договора. Все авторские права на произведения принадлежат авторам и охраняются законом. Перепечатка произведений возможна только с согласия его автора, к которому вы можете обратиться на его авторской странице. Ответственность за тексты произведений авторы несут самостоятельно на основании правил публикации и законодательства Российской Федерации. Данные пользователей обрабатываются на основании Политики обработки персональных данных. Вы также можете посмотреть более подробную информацию о портале и связаться с администрацией.

Вложение	Размер
Неевклидова геометрия	775.58 КБ

Предварительный просмотр:

МКОУ ВАШУТИНСКАЯ ОСНОВНАЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА

История возникновения и значение неевклидовой геометрии в современной науке

Работу по геометрии выполнила:

ученица 9 класса

Седых Елена Валерьевна

2.История создания новой геометрии………………………………. 4

3. Неевклидова геометрия…………………………………………… 8

4.Отзывы и доказательства …………………………………………. 11

4. Значение Неевклидовой геометрии……………………………… 15

6.Используемая литература…………………………………………. 18

Тот путь, на который впервые стал Лобачевский, в значительной степени определил лицо современной науки, произвёл настоящую революцию в математике.

Открытие неевклидовой геометрии произвело переворот не только в геометрии и даже не только в математике, но можно сказать, в развитии человеческого мышления вообще. И то , что евклидова геометрия не является единственно возможной, сделанное в начале прошлого века Гауссом, Лобачевским и Больяи, оказало влияние на мировоззрение человечества. Однако мало кому известно, что начиная с конца прошлого века неевклидова геометрия, наряду с евклидовой, является одним из рабочих инструментов математики, несмотря на то что "пространство, в котором мы живем", в доступных нашему пониманию пределах является скорее евклидовым, чем неевклидовым [ 2].

Характер математических теорий таков, что различным образом представляя основные понятия этих теорий, в геометрии, например, это точки, прямые, движения и т.д., мы можем применять их к объектам различного рода. Поэтому, и геометрия может применяться не только к пространству, в котором мы живем, но и к другим пространствам, возникающим в математических и физических теориях. Геометрии этих пространств оказываются различными; в частности, они могут не быть евклидовыми.

Цель работы : установить, что послужило созданию неевклидовой геометрии. Гипотеза : развитие науки было на таком этапе, что невозможно было не прийти к созданию неевклидовой геометрии.

I.История создания новой геометрии

Рисунок 1. Евклид

Одновременно и независимо к аналогичным выводам пришёл Янош Бойяи (рис.2), а Карл Фридрих Гаусс (рис.3) пришёл к таким выводам ещё раньше.

Рисунок 2. Янош Бойяи

Однако труды Бойяи не привлекли внимания, и он вскоре оставил эту тему, а Гаусс вообще воздерживался от публикаций, и о его взглядах можно судить лишь по нескольким письмам и дневниковым записям.

Рисунок 3 . Карл Фридрих Гаусс

Из Академии наук пришел уничтожающий отзыв, появляются статьи, где Лобачевского называют провинциальным шарлатаном, невежественным самодовольным ничтожеством. Авторы этих отзывов опирались на то, что все, что изложено господином Лобачевским (рис.4) в своих трудах не имеет места в природе и, поэтому, совершенно для разума непонятно и абсурдно. Лобачевского никто не поддержал, но у него хватило мужества отстаивать свои идеи до конца.

Рисунок 4. Лобачевский Николай Иванович

Пятый постулат Евклида стал своего рода толчком к созданию другой геометрии, или продолжением геометрии Евклида. Одновременно учёные многих стран пришли к одним и тем же выводам. Однако одних учёных не поняли, как Лобачевского, другие боялись опубликовать свои труды.

Создателями неевклидовой геометрии стали такие яркие учёные, как сам Евклид, Гаусс, Бойяи, Лобачевский. У некоторых учёных открытия в неевклидовой геометрии происходили одновременно, независимо друг от друга.

Лобачевский считал аксиому параллельности Евклида произвольным ограничением. С его точки зрения, это требование слишком жёсткое, ограничивающее возможности теории, описывающей свойства пространства, и поэтому в создании неевклидовой геометрии он использовал плоскостные постулаты Евклида как частный, предельный случай и отказался от V постулата, приняв независимость аксиомы о параллельных прямых Евклида от остальных аксиом.

Через точку С, лежащую вне прямой АВ, можно, предположил Лобачевский, провести хотя бы две прямые а и b, которые не пересекутся с прямой АВ (рис.5). Точно так же не пересекают прямую АВ и прямые m, n, p, проходящие через точку С. [4].

Рисунок 5. Предложение, противоположное V постулату Евклида.

Рисунок 6. Треугольник в геометрии Лобачевского.

В плоскости Лобачевского не существует никакого подобия. Ведь все теоремы о подобии выводятся только с помощью аксиомы Евклида о параллельности. Н.И. Лобачевский установил, что на предельной поверхности, называемой орисферой, внутренняя геометрия является евклидовой.

Разработанная Лобачевским новая геометрия не включает в себя евклидову геометрию, однако евклидова геометрия может быть из неё получена предельным переходом (при стремлении кривизны пространства к нулю). В самой геометрии Лобачевского кривизна отрицательна. Уже в первой публикации Лобачевский детально разработал тригонометрию неевклидова пространства, дифференциальную геометрию (включая вычисление длин, площадей и объёмов) и смежные аналитические вопросы.

В пространстве Лобачевского были выделены криволинейные геометрические образы, подчинённые геометрии Евклида. Этот замечательный результат Лобачевский использовал для вывода тригонометрических соотношений между элементами прямолинейных треугольников в его пространстве. Но итоговые соотношения гораздо сложнее евклидовых. Эти соотношения имеют не только тригонометрические функции углов, не просто длины сторон, а некоторые функции от них [ 4] .

Сделав свое знаменитое открытие, Н. И. Лобачевский не опроверг евклидову геометрию, а лишь раздвинул границы науки, существовавшей в Древнем мире. Любые факты планиметрии Лобачевского не противоречат геометрии Евклида. Однако созданная геометрия существенно отличается от прежней. Лобачевский, очевидно, хотел подчеркнуть противоречие V постулату: на плоскости через точку, лежащую вне данной прямой, проходит более одной прямой, не пересекающей данную. И тем самым заменил евклидов постулат более общей аксиомой параллельности и сохранил все рассуждения геометрии Евклида.

III. Отзывы и доказательства

В последние годы жизни Лобачевский безуспешно пытался доказать непротиворечивость своей геометрии.

Чтобы получить такое доказательство, надо было построить модель геометрии. В 1868 году (через 12 лет после смерти Лобачевского) итальянский ученый Э. Бельтрами исследовал вогнутую поверхность называемую псевдосферой и доказал, что на этой поверхности действует геометрия Лобачевского (рис.7). [ 5].

В 1868г. Итальянский математик Э. Бельтрами исследовал вогнутую поверхность, называемую псевдосферой, и доказал, что на этой поверхности действует геометрия Лобачевского.

Рисунок 7. Псевдосфера

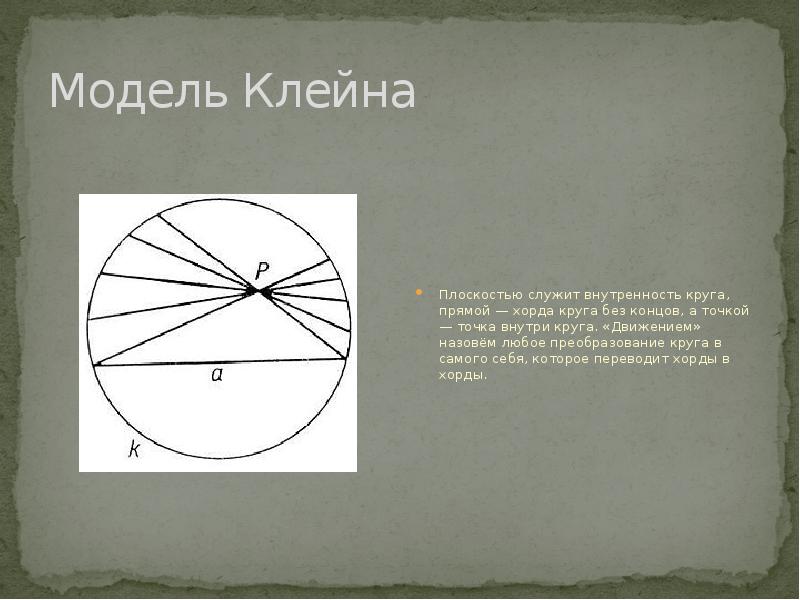
А через 2 года немецкий математик Клейн предлагает другую модель плоскости Лобачевского (рис.8).

Рисунок 8. Модель Клейна.

Рисунок 9 . Модель Пуанкаре.

В конце прошлого века в работах Пуанкаре и Клейна была установлена прямая связь геометрии Лобачевского с теорией функций комплексной переменной и с теорией чисел (точнее, арифметикой неопределенных квадратичных форм). С тех пор аппарат геометрии Лобачевского стал неотъемлемым компонентом этих разделов математики. В последние 15 лет значение геометрии Лобачевского еще более возросло благодаря работам американского математика Тёрстона (лауреата Филдсовской медали 1983 г.), установившего ее связь с топологией трехмерных многообразий (рис.10). Десятки работ ежегодно публикуются в этой области. В связи с этим можно говорить о конце романтического периода в истории геометрии Лобачевского, когда основное внимание исследователей было обращено на ее осмысление с точки зрения оснований геометрии вообще. Современные исследования все больше требуют делового владения геометрией Лобачевского [ 2].

Рисунок 10. Вильям Паул Тёрстон

Важное замечание, касающееся чертежей, изображающих поведение прямых на плоскости Лобачевского. Как показывают опыты, наше физическое пространство по свойствам или евклидово, или очень мало от него отличается. Оперируя с чертежом, вынуждены ограничиться его малым размером, а отклонение от евклидовости, если оно существует, будет наблюдаться только при очень больших протяжениях. Поэтому для наглядности обычно принято изображать прямые, слегка их искривляя, чтобы отчётливее выразить характер их сближения или расхождения на плоскости Лобачевского. Однако Лобачевский такие вольности себе не разрешал[ 4].

Сколько времени нужно было учёным, чтобы проверить на различных моделях: псевдосфере Клейна, модель Пуанкаре, трёхмерные многообразия математика Тёрстона, что геометрия Лобачевского действует? Какие сомнения возникали у самого Лобачевского в правильности его идей?! Но именно элементы геометрии Лобачевского стали основой таких разделов математики, как теория чисел и теория функций комплексной переменной и многих других.

IV. Значение Неевклидовой геометрии

Открытие новой геометрии стало началом многочисленных исследований выдающихся математиков 19 века. Геометрия послужила толчком к развитию науки, а значит и пониманию мира, который на окружает.

А в начале 20-говека было обнаружено, что геометрия Лобачевского совершенно необходима в современной физике. Например, в теории относительности Эйнштейна, в расчетах современных синхрофазотронов, в космонавтике.

Создателями неевклидовой геометрии стали такие яркие учёные, как сам Евклид, Гаусс, Бойяи, Лобачевский. Евклид делал попытки доказать пятый постулат, но у него не получалось. У некоторых учёных открытия в неевклидовой геометрии происходили одновременно, независимо друг от друга.

Н. И. Лобачевский раздвинул границы науки, существовавшей на тот момент. Любые факты планиметрии Лобачевского не противоречат геометрии Евклида. Однако созданная геометрия существенно отличается от прежней. Лобачевский, очевидно, хотел подчеркнуть противоречие V постулату: на плоскости через точку, лежащую вне данной прямой, проходит более одной прямой, не пересекающей данную. И тем самым заменил евклидов постулат более общей аксиомой параллельности и сохранил все рассуждения геометрии Евклида.

Много времени понадобилось учёным, чтобы проверить на различных моделях: псевдосфере Клейна, модель Пуанкаре, трёхмерные многообразия математика Тёрстона, что геометрия Лобачевского действует? Какие сомнения возникали у самого Лобачевского в правильности его идей?! Но именно элементы геометрии Лобачевского стали основой таких разделов математики, как теория чисел и теория функций комплексной переменной и многих других.

Вы можете изучить и скачать доклад-презентацию на тему Неевклидова геометрия. Презентация на заданную тему содержит 20 слайдов. Для просмотра воспользуйтесь проигрывателем, если материал оказался полезным для Вас - поделитесь им с друзьями с помощью социальных кнопок и добавьте наш сайт презентаций в закладки!

Выполнил: ученик 10 А класса Чуриков Сергей Юрьевич Руководитель проекта: учитель математики Пласкунова Надежда Анатольевна

Введение Много веков геометрия во всех своих основах казалась наукой, совершенно застывшей в ее древних эллинских формах. Ученых всех времен интересовало доказательство или опровержение V постулата Евклида, одного из основных для его геометрии. В XIX веке Николай Иванович Лобачевский одним из первых доказал возможность существования геометрии, отличной от Евклидовой. Его идеи привели к широкой и многообразной эволюции геометрии. Изучение этой геометрии способствует лучшему пониманию законов физического пространства, т.к. геометрия Евклида описывает пространство приближенное, идеальное. Геометрия Лобачевского более точная, она учитывает кривизну пространства-времени. В школе мы изучаем геометрию Евклида. А живем мы в какой геометрии? Неевклидова геометрия - это другая геометрия, отрицающая Евклидову? Как новые геометрические идеи повлияли на развитие естествознания? Как развиваются неевклидовы геометрии? Исследованию этих вопросов посвящен этот проект. В процессе работы были рассмотрены основные положения геометрии Лобачевского, доказана её непротиворечивость, рассмотрены сферы её применения в реальной жизни. Для освещения основных положений изучалась специальная литература, для доказательства противоречивости рассмотрены простейшие модели, на которых справедлива геометрия Лобачевского.

История развития геометрии Геометрия- одна из древнейших наук. Её возникновение связано с практическими занятиями человека.

Аристотель Основные принципы дедуктивного построения науки впервые были сформулированы Аристотелем. Он считал, что доказывая то или иное утверждение, необходимо опираться на ранее доказанные. Из этого следует, что существуют утверждения, с которых начинается построение науки. Такие утверждения называются аксиомами и не требуют доказательств.

Постулаты Евклида 1. От всякой точки до всякой точки можно провести прямую. 2. Ограниченную прямую можно непрерывно продолжать по прямой. 3. Из всякого центра и всяким раствором может быть описан круг. 4. Все прямые углы равны между собой. 5. Если прямая, падающая на две прямые, образует внутренние односторонние углы, в сумме меньшие двух прямых, то, продолженные неограниченно, эти две прямые встретятся с той стороны, где углы в сумме меньше двух прямых.

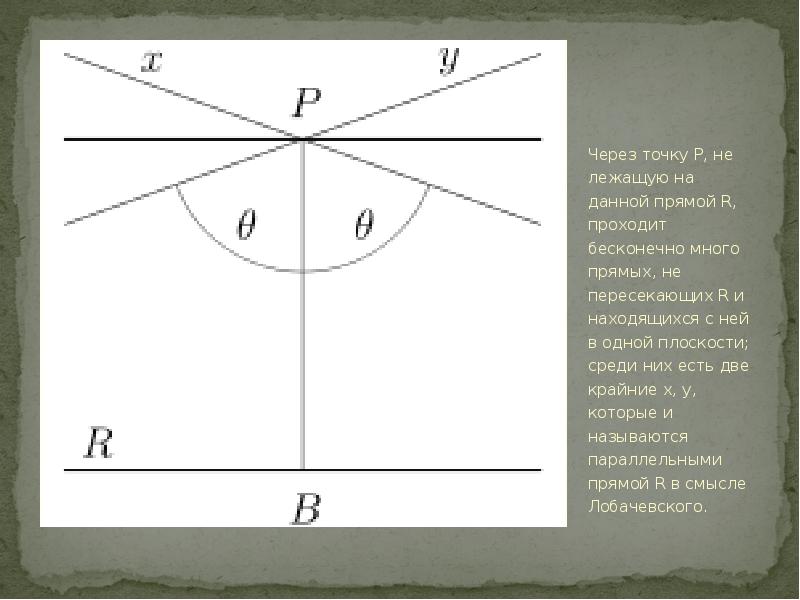
Через точку P, не лежащую на данной прямой R, проходит бесконечно много прямых, не пересекающих R и находящихся с ней в одной плоскости; среди них есть две крайние x, y, которые и называются параллельными прямой R в смысле Лобачевского.

Псевдосфера Э.Бельтрами Если точкам и прямым на конечном куске плоскости Лобачевского сопоставлять точки и кратчайшие линии (геодезические) на псевдосфере и движению в плоскости Лобачевского сопоставлять перемещение фигуры по псевдосфере с изгибанием, то есть деформацией, сохраняющей длины, то всякой теореме геометрии Лобачевского будет отвечать факт, имеющий место на псевдосфере. При этом длины, углы, площади понимаются в смысле естественного измерения их на псевдосфере. Но эта модель является локальной интерпретацией геометрии, неспособной отобразить всю плоскость Лобачевского.

Геометрия Лобачевского в наши дни В наши дни геометрия Лобачевского используется в космонавтике для прокладывания дальних маршрутов, вычисления траектории полета, в современной физике и во многих других естественных науках.

Хотелось бы остановиться на эволюции принципа относительности в физике и её связи с геометрией. Теория относительности – теория, описывающая универсальные пространственно-временные свойства физических процессов.

Мифы о неевклидовой геометрии Миф первый. Геометрия Лобачевского не имеет ничего общего с Евклидовой. Миф второй. В теории Лобачевского параллельные прямые пересекаются. Миф третий. Геометрия Лобачевского - единственная неевклидова геометрия. Миф четвертый. Геометрия Лобачевского не применима в реальной жизни. Миф пятый. Лобачевский первым создал неевклидову геометрию.

Выводы В процессе работы рассмотрены основные положения геометрии Лобачевского, доказана её непротиворечивость, указаны некоторые сферы её применения в реальной жизни: в физике( в частности астрономии и космонавтике) и многих других естественных науках. Работа показывает существование геометрии, отличной от Евклидовой, ее суть и развитие. Изучая литературу я понял ,что из неевклидовой геометрии пошел новый научный замысел. В прежние времена одна научная теория сменяла другую, стирая прежнюю. Теперь стала действовать другая схема: теория, объясняющая явления по существу, но все же с дефектами в отдельных пунктах, заменяется более общей, содержащей параметры, при частных значениях которых она возвращается к установившейся. На основе идей Н.И. Лобачевского геометрия разрослась в огромное здание, в котором, изучаемая нами, геометрия Евклида составляет основной камень в его фундаменте. Неевклидова геометрия почти полностью решила задачу обоснования геометрии Евклида и дала схему обоснования всякой дедуктивной науки. Неевклидова геометрия получила применение в анализе и теории функций –одном из основных вопросов теории познания. Она в широком смысле составляет базу важнейших учений современной физики. Развитие неевклидовой геометрии продолжается. Поставленная перед проектом цель достигнута.

НЕЕВКЛИДОВА ГЕОМЕТРИЯ, геометрия, сходная с геометрией Евклида в том, что в ней определено движение фигур, но отличающаяся от евклидовой геометрии тем, что один из пяти ее постулатов (второй или пятый) заменен его отрицанием. Отрицание одного из евклидовых постулатов (1825) явилось значительным событием в истории мысли, ибо послужило первым шагом на пути к теории относительности.

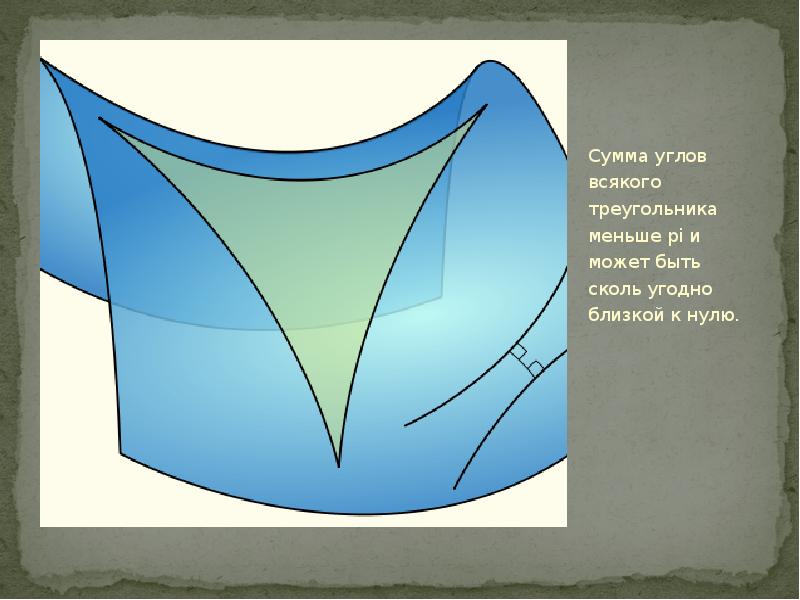
Из этих пересмотренных постулатов следовало, что сумма углов треугольника, равная 180 ° в евклидовой геометрии, больше 180 ° в эллиптической геометрии и меньше 180 ° в гиперболической геометрии.

История.

В 1854 Б.Риман (1826–1866) заметил, что из неограниченности пространства еще не следует его бесконечная протяженность. Смысл этого утверждения станет яснее, если представить, что в неограниченной, но конечной вселенной астроном в принципе мог бы увидеть в телескоп, обладающий достаточно высокой разрешающей способностью, свой собственный затылок (если отвлечься от небольшой детали, связанной с тем, что свет, отраженный от затылка, достиг бы глаза астронома через тысячи миллионов лет). В своем доказательстве того, что внешний угол при любой вершине треугольника больше внутреннего угла при любой из двух остальных вершин, Евклид неявно использовал бесконечную длину прямой. Из этой теоремы тотчас же следует теорема о том, что сумма любых двух углов треугольника меньше суммы двух прямых углов. Если отказаться от бесконечной длины прямой, то гипотеза Саккери о тупом угле становиться верной и из нее следует, что сумма углов треугольника больше суммы двух прямых. Такое положение дел было давно известно в сферической тригонометрии, где стороны треугольника являются дугами больших кругов. Риман внес эпохальный вклад, распространив представление о конечном, но неограниченном пространстве с двух на три и большее число измерений.

Эллиптическая плоскость.

Геометрия порядка.

Абсолютная геометрия.

Гиперболическая плоскость.

П(x) = 2arctg e –x .

Евклидовы модели неевклидовых геометрий.

А.Пуанкаре (1854–1912) открыл представление гиперболического пространства с помощью конформной модели, в которой геометрическое место концов имеет вид плоскости W в евклидовом пространстве, а сферам с центрами в W соответствуют плоскости гиперболического пространства. Заменив сферы полусферами, Пуанкаре получил возможность представить все гиперболическое пространство с помощью половины евклидова пространства, а именно всеми точками, лежащими по одну сторону от W . Один пучок концентрических орисфер представлен плоскостями, параллельными W ; можно доказать, что евклидовы расстояния в такой плоскости пропорциональны соответствующим геодезическим на орисфере, что полностью согласуется с наблюдением Вахтера.

Рассматривая сечение трехмерной модели Пуанкаре плоскостью, перпендикулярной W , мы получим модель аналогичную модели Пуанкаре для гиперболической плоскости. В этой модели геометрическое место концов имеет вид евклидовой прямой. В другой модели геометрическое место концов имеет вид окружности w , а прямые на гиперболической плоскости – дуг окружностей, ортогональных w . Две параллельные дуге r, проходящие через точку B, – просто дуги, проходящие через точку B и касающиеся дуги r в ее концах, как на рис. 5.

Читайте также: