Доклад о многоугольниках или треугольниках

Обновлено: 04.07.2024

Вы можете изучить и скачать доклад-презентацию на тему Многоугольники. Виды многоугольников. Презентация на заданную тему содержит 13 слайдов. Для просмотра воспользуйтесь проигрывателем, если материал оказался полезным для Вас - поделитесь им с друзьями с помощью социальных кнопок и добавьте наш сайт презентаций в закладки!

Содержание. Определение _____________________ Слайд № 4 Из чего состоит многоугольник? ____ Слайд № 5 Виды многоугольников ____________ Слайд № 6 Формулы ________________________ Слайд № 9 Медианы, диагонали, высоты и биссектрисы _____ ____________________________________ Слайд № 10 Окружность и многоугольник ______ Слайд № 11 Заключение ______________________ Слайд № 12

Определение. Давайте подумаем на счёт того, что же такое многоугольник. Многоугольник – это геометрическая фигура, состоящая из замкнутой ломанной и имеющая более 1 угла (вершины). Из определения можно сделать вывод, что любая замкнутая фигура является многоугольником. Многоугольник является обобщением для ряда других замкнутых фигур, таких как треугольники, четырёхугольники, пятиугольники и т. д.

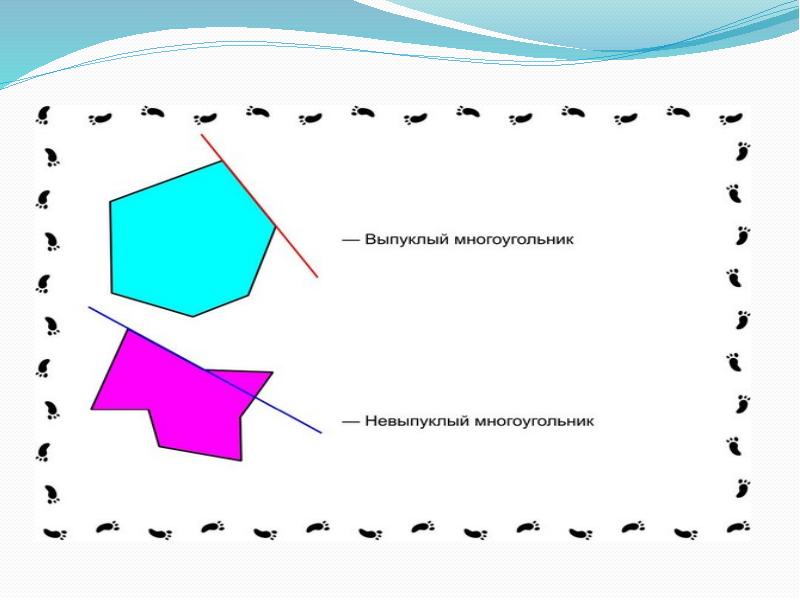
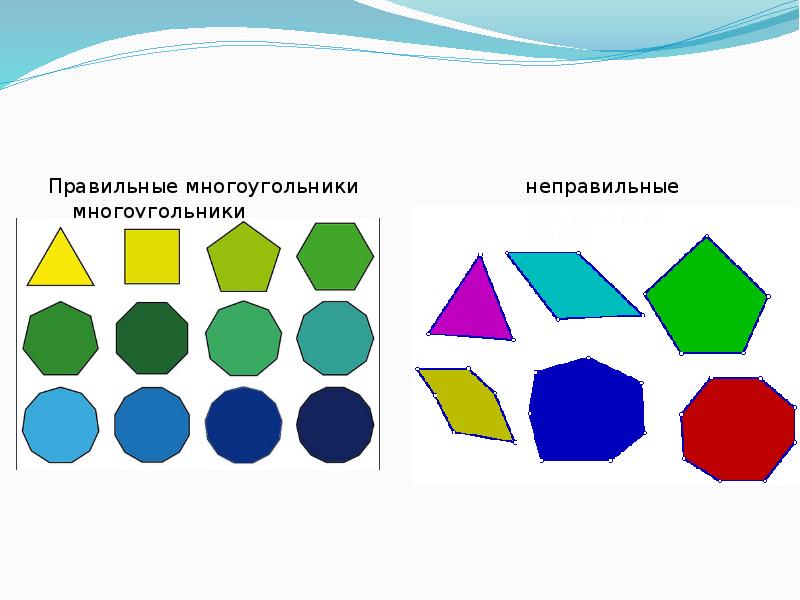
Виды многоугольников. Многоугольники бывают выпуклыми и невыпуклыми (Выпуклый многоугольник – это многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через 2 его соседние вершины). А выпуклые в свою очередь подразделяются на правильные и неправильные (Правильный многоугольник – это выпуклый многоугольник, у которого все стороны и углы равны). Также многоугольники делятся на: Треугольники. Треугольник – это многоугольник, состоящий из 3 вершин, не лежащих на одной прямой и соединённые смежными отрезками. Четырёхугольники (Определение схожее с треугольниками). N-угольники. N-угольники – это фигуры, имеющие n-количество вершин и сторон.

Определение 1. Многоугольник − замкнутая ломаная линия.

Объединение многоугольника и ограниченной им части плоскости также называют многоугольником. Поэтому представим другое определение многоугольника:

Определение 2. Многоугольник − это геометрическая фигура, которая является частю плоскости, ограниченная замкнутой ломаной.

Вершины ломаной называются вершинами многоугольника. Звенья ломаной называются сторонами многоугольника.

Любой многоугольник разделяет плоскость на две части, одна из которых называется внутренней областью многоугольника, а другая внешней областью многоугольника.

Виды многоугольников

Многоугольник с тремя вершинами называется треугольником, с четыремя вершинами − четырехугольником, с пяти вершинами − пятиугольником, и т.д. Многоугольник с \( \small n \) вершинами называется \( \small n- \)угольником.

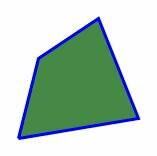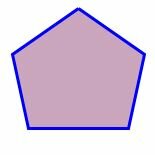На рисунке 1 представлены различные виды многоугольников.

Обозначение многоугольника

Обозначают многоугольник буквами, стоящих при его вершинах. Называют многоугольник чередовав буквы при его вершинах по часовой стрелке или против часовой стрелки. Например, многоугольник на рисунке 2 называют \( \small A_1A_2A_3A_4A_5A_6 \) или \( \small A_6A_5A_4A_3A_2A_1 \).

Соседние вершины многоугольника

Вершины многоугольника называются соседними, если они являются концами одной из его сторон.

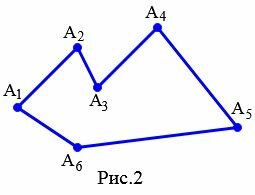На рисунке 2 вершины \( \small A_2 \) и \( \small A_3 \) являются соседними, так как они являются концами стороны \( \small A_2A_3. \)

Смежные стороны многоугольника

Стороны многоугольника называются смежными, если они имеют общую вершину.

На рисунке 2 стороны \( \small A_4A_5 \) и \( \small A_5A_6 \) являются смежными, так как они имеют общую вершину \( \small A_5. \)

Простой многоугольник. Самопересекающийся многоугольник

Многоугольник называется простым, если его несмежные стороны не имеют общих точек (внутренних или концевых).

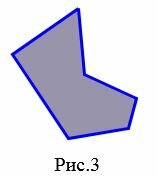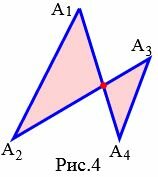На рисунке 3 изображен простой многоугольник так как стороны многоугольника не имеют самопересечений. А на рисунке 4 многоугольник не является простым, так как стороны \( \small A_1A_4 \) и \( \small A_2A_3 \) пересекаются. Такой многоугольник называется самопересекающийся многоугольник.

Выпуклый многоугольник

Многоугольник называется выпуклым, если она лежит по одну сторону от прямой, проходящей через любую его сторону.

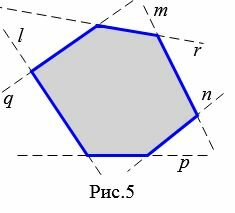На рисунке 5 многоугольник лежит по одну сторону от прямых \( \small m, \ n, \ l, \ p, \ q, \ r\) проходящих через стороны многоугольника.

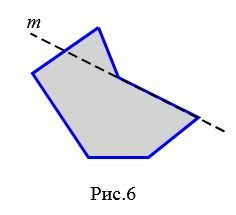На рисунке 6 прямая \( \small m\) делит многоугольник на две части, т.е. многоугольник не лежит по одну сторону от прямой \( \small m\). Следовательно многоугольник не является выпуклым.

Правильный многоугольник

Простой многоугольник называется правильным, если все его стороны равны и все углы равны. Например равносторонний треугольник является правильным многоугольником, поскольку все его стороны равны, и все его углы равны 60°. Квадрат является правильным многоугольником, так как все его стороны равны и все его углы равны 90°.

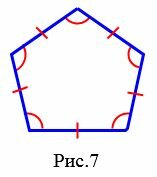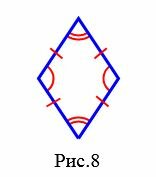На рисунке 7 изображен правильный многоугольник (пятиугольник), так как у данного многоугольника все стороны равны и все углы равны. Многоугольник (ромб) на на рисунке 8 не является правильным, так как все стороны многоугольника равны, но все углы многоугольника не равны друг другу. Прямоугольник также не является правильным многоугольником, так как несмотря на то, что все углы прямоугольника равны, но все четыре стороны прямоугольника не равны друг другу.

Звездчатый многоугольник

Самопересекающийся многоугольник, все стороны которого равны и все углы равны, называется звездчатым или звездчато-правильным.

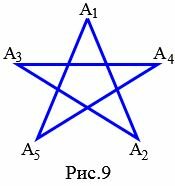На рисунке 9 представлен звездчатый пятиугольник поскольку все углы \( \small A_1, \ A_2, \ A_3, \ A_4, \ A_5 \) равны и равны все стороны: \( \small A_1A_2=A_2A_3=A_3A_4=A_4A_5=A_5A_1. \)

Периметр многоугольника

Сумма всех сторон многоугольника называется периметром многоугольника. Для многоугольника \( \small A_1A_2. A_A_n \) периметр вычисляется из формулы:

Угол многоугольника

Углом (внутренним углом) многоугольника при данной вершине называется угол между двумя сторонами многоугольника, сходящимися к этой вершине. Если многоугольник выпуклый, то все углы многоугольника меньше 180°. Если же многоугольник невыпуклый, то он имеет внутренний угол больше 180° (угол \( \small A_3 \) на рисунке 2).

Внешний угол многоугольника

Внешним углом многоугольника при данной вершине называется угол смежный внутреннему углу многоугольника при данной вершине.

На рисунке 10 угол 1 является внешним углом данного многоугольника при вершине \( \small E. \)

Диагональ многоугольника. Количество диагоналей

Диагоналями называют отрезки, соединяющие две несоседние вершины многоугольника.

Выведем форулу вычисления количества диагоналей многоугольника. Пусть задан \( \small n \)-угольник. Выберем одну вершину многоугольника и проведем мысленно все отрезки, соединяющие эту вершину с остальными вершинами. Получим \( \small n-1 \) отрезков. Но поскольку две вершины для выбранной вершины являются соседними, а по определнию диагональ − это отрезок соединяющий несоседние вершины, то из \( \small n-1 \) вычтем 2. Получим \( \small n-3 \). Всего \( \small n \) вершин. Следовательно количество вычисленных диагоналей будет \( \small n(n-3). \) Учитывая, что каждый диагональ − это отрезок соединяющий две вершины, то получится, что мы вычислили каждый диагональ дважды. Поэтому полученное число нужно делить на два. Получим количество диагоналей \( \small n- \)мерного многоугольника:

Сумма углов выпуклого многоугольника

Выведем формулу вычисления суммы углов выпуклого многоугольника. Для этого проведем из вершины \( \small A_1 \) все диагноали многоугольника \( \small A_1A_2. A_A_n \) (Рис.11):

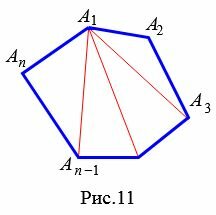Количество диагоналей, проведенной из одной вершиы, как выяснили из предыдующего параграфа равно \( \small n-3 \). Следовательно, эти диагонали разделяют многоугольник на \( \small n-3+1=n-2 \) треугольников. Поскольку сумма углов треугольника равна 180°, то получим, что сумма углов выпуклого многоугольника равна: \( \small 180°(n-2). \)

где \( \small n \) −количество сторон (вершин) выпуклого многоугольника.

Угол правильного многоугольника

Поскольку у правильного многоугольника все углы равны, то используя формулу (1) получим угол правильного многоугольника:

где \( \small n \) −количество сторон (вершин) правильного многоугольника.

Никогда не было интересно, почему в треугольнике 180 градусов?

А в других фигурах сколько? Да постой, положи транспортир!

Сейчас ты узнаешь много нового о такой, казалось бы, простой теме, как многоугольники.

Многоугольники — коротко о главном

Многоугольник – это замкнутая линия, которая образовывается, если взять \( \displaystyle n\) каких-либо точек \( \displaystyle >,\text< >>,\text< >…,~>\) и соединить их последовательно отрезками.

Многоугольник с \( \displaystyle n\) сторонами называют \( \displaystyle n\)-угольником.

Например: многоугольник c \( \displaystyle 4\) сторонами называют четырехугольником, многоугольник с \( \displaystyle 6\) сторонами — шестиугольником и так далее по аналогии.

Выпуклый многоугольник – многоугольник лежащий по одну сторону от любой прямой, соединяющей его соседние вершины.

Сумма внутренних углов выпуклого n-угольника равна \( \displaystyle 180<>^\circ \cdot (n-2)\) или \( \displaystyle _>+_>+\text< >…~+_>\), где \( \displaystyle _>\) – внутренний угол многоугольника.

Правильный выпуклый многоугольник – многоугольник все стороны и внутренние углы которого равны.

Внутренний угол правильного \( \displaystyle n\)-угольника равен \( \displaystyle \alpha =\frac\cdot 180<>^\circ \).

Любой правильный многоугольник можно вписать в окружность и вокруг любого правильного многоугольника можно описать окружность.

Центры вписанной в правильный многоугольник окружности и окружности, описанной около него, совпадают.

Если многоугольник такой, что в него можно вписать окружность, то его площадь выражается формулой: \( \displaystyle S=pr\), где \( \displaystyle p=\frac>>+>>+…+>>>\).

Многоугольник — подробнее

Многоугольник – это замкнутая линия, которая образовывается, если взять \( \displaystyle n\) каких-либо точек \( \displaystyle >,\text< >>,\text< >…,~>\) и соединить их последовательно отрезками.

При этом смежные стороны (имеющие общую вершину) не должны лежать на одной прямой, а несмежные стороны не должны иметь общих точек (то есть не должны пересекаться).

Многоугольник с \( \displaystyle n\) сторонами называют \( \displaystyle n\)-угольником.

Произвольные многоугольники

Давай-ка нарисуем, какие бывают многоугольники.

А теперь вопрос: какой из этих многоугольников выпадает из ряда?

Посмотри внимательно на второй многоугольник — он отличается от всех остальных. Чем же?

Это не выпуклый многоугольник. Это, конечно, математическое название, но с человеческой интуицией не расходится.

Ну вот, а мы будем рассматривать только выпуклые многоугольники, то есть такие, как 1),3),4) и т.п.

Итак, основной факт:

Давай сразу к примерам:

Четырехугольник

Пятиугольник

Шестиугольник

Ах да, про треугольник забыли.

Треугольник

Сумма углов многоугольника. Доказательство.

А теперь давай все-таки разберемся, откуда же взялась формула суммы углом многоугольника \( \displaystyle 180^\circ(n-2)\).

Понимаешь, приемчик, который мы сейчас применим, часто оказывается полезным при решении разных задач.

Несмотря на то, что теорема о сумме углов многоугольника верна для всякого многоугольника, доказательство красивое и простое только для выпуклых многоугольников.

Итак, давай разделим многоугольник на треугольники.

Вот так: из одной точки проведем все диагонали, что можно. Сколько их будет? Считаем:

Всего вершин: \( \displaystyle n\)

Из вершины \( \displaystyle B\) можем провести диагонали во все вершины, кроме:

Самой вершины B
Вершины A
Вершины C

Значит всего диагоналей \( \displaystyle (n-3)\). А на сколько треугольников распался наш многоугольник?

Представь себе: на \( \displaystyle n-2\). Порисуй, посчитай – удостоверься, что треугольников оказывается ровно на один больше.

Итак, у нас ровно \( \displaystyle n-2\) треугольника. И сумма углов многоугольника просто равна сумме углов треугольников, на которые мы разбили многоугольник.

Чему равна сумма углов треугольника? Помнишь? Конечно \( \displaystyle 180<>^\circ \).

Ну вот, \( \displaystyle n-2\) треугольника, в каждом по \( \displaystyle 180<>^\circ \), значит:

Сумма углов многоугольника равна \( \displaystyle 180<>^\circ \)\( \displaystyle (n-2)\)

Что же из этого может оказаться полезным? Два момента:

Читать далее…

Мы хотим постоянно улучшать этот учебник и вы можете нам в этом помочь.
Оформите доступ и пользуйтесь учебником ЮКлэва без ограничений (100+ статей по всем темам ОГЭ и ЕГЭ, 2000+ разобранных задач, 20+ вебинаров-практикумов)

Правильные многоугольники

Многоугольник называется правильным, если все его углы и все его стороны равны.

Так, например: квадрат – правильный четырехугольник, а вот прямоугольник – нет, хоть и все углы у него равные, и ромб – нет, хоть и все стороны равны. Нужно непременно, чтобы все углы и все стороны были равны.

Первый вопрос:

А можно ли найти величину одного (а значит и всех) угла правильного многоугольника?

Давай посмотрим на примере.

Пусть есть, скажем, правильный восьмиугольник:

А сколько всего углов? Восемь конечно, и они все одинаковые.

Значит любой угол, скажем \( \displaystyle \angle A\) можно найти:

\( \displaystyle \angle A=\frac^\circ >=135<>^\circ \).

Что мы еще должны знать?

Любой правильный многоугольник можно вписать в окружность и вокруг любого правильного многоугольника можно описать окружность.

При этом центры этих окружностей совпадают.

Смотри, как это выглядит!

И более того, всегда можно посчитать соотношение между радиусом вписанной и описанной окружностей.

Давай опять на примере восьмиугольника.

Посмотри на \( \displaystyle \Delta OKG\). В нем \( \displaystyle OK=r,OG=R.\)

Значит, \( \displaystyle \frac=\sin \angle x\) – и это не только в восьмиугольнике!

Чему же равен в нашем случае \( \displaystyle \angle x\)?

Ровно половине \( \displaystyle \angle G\), представь себе!

Значит \( \displaystyle \angle x=\frac^\circ >=67,5<>^\circ \).

Смешно? Но так и есть! Поэтому для восьмиугольника \( \displaystyle \frac=\sin 67,5<>^\circ \).

И тот же ответ: конечно можно!

Опять рассмотрим наш восьмиугольник. Вот мы хотим найти \( \displaystyle \angle \alpha\) (то есть \( \displaystyle \angle HOG\)).

Читать далее…

И так можно все находить не только для восьмиугольника, но и для любого правильного многоугольника.

Бонус. Вебинар из нашего курса подготовки к ЕГЭ по математике

ЕГЭ 6. Описанная окружность. Многоугольники

Вы этом видео вы узнаете, что такое описанная окружность, где находится её центр, и другие свойства.

Около каких фигур можно, а вокруг каких нельзя описать окружность.

Также мы узнаем, что такое правильные многоугольники, и какие у них свойства; как они связаны с описанной окружностью.

Научимся решать задачи из ЕГЭ на описанную окружность и правильные многоугольники.

Наши курсы по подготовке к ЕГЭ по математике, информатике и физике

Курсы для тех, кому нужно получить 90+ и поступить в топовый ВУЗ страны.

Алексей Шевчук — ведущий курсов

А теперь твоя очередь!

Теперь ты знаешь все о многоугольниках!

Особенно эти знания пригодятся тебе, когда будешь решать задачи про окружности. Задачи олимпиадного уровня. Да и просто так знать полезно 🙂

А сейчас мы хотим услышать тебя. Понравилась ли тебе статья? Ты во всем разобрался?

Кстати, пытался строить многоугольники циркулем?

Напиши в комментариях ниже!

И задай любые вопросы, если они возникли! Мы непременно ответим!

Добавить комментарий Отменить ответ

3 комментария

Даша :

Як разбить чатырох угольник так, чтоб палучился трохвугольник и чатырохвугольник

Алексей Шевчук :

Даша, например, можно провести отрезок из вершины в середину противоположной стороны.

Александр Кель :

Некоторые комментарии прошлых лет к этой статье:

Сергей
19 февраля 2018
Просто огромное спасибо. Хоть что-то начал понимать.

Александр (админ)
19 февраля 2018
Просто огромное пожалуйста. 🙂 Очень приятно слышать от вас такие слова.

Вероника
18 марта 2020
Спасибо большое, а то на карантине приходится самим разбирать темы!

Сима
01 июля 2020
Блин, действительно очень круто изложили. А главное- понятно и просто. Начала подготовку к егэ, в следующем году сдавать. Очень помогли разобраться с этой темой! Спасибо)

Александр (админ)
01 июля 2020
Блин, Сима, до чертиков приятно слышать такие слова! 🙂 Если начала подготовку к ЕГЭ, то будь на связи, мы сейчас делаем крутейший курс подготовки к ЕГЭ, где вот так вот просто все будет объяснять Алексей Шевчук.

Треугольник – это геометрическая фигура, которая состоит из трёх точек, не лежащих на одной прямой (вершин треугольника) и трёх отрезков с концами в этих точках (сторон треугольника).

Углами (внутренними углами) треугольника называются три угла, каждый из которых образован тремя лучами, выходящими из вершин треугольника и проходящими через две другие вершины.

Внешним углом треугольника называется угол, смежный внутреннему углы треугольника.

Сумма углов треугольника равна 180°:

Внешний угол равен сумме двух внутренних углов, не смежных с ним, и больше любого внутреннего, с ним не смежного:

Длина каждой стороны треугольника больше разности и меньше суммы длин двух других сторон:

В треугольнике против большего угла лежит большая сторона, против большей стороны лежит больший угол:

Средней линией треугольника называется отрезок, который соединяет середины двух его сторон.

Средняя линия треугольника параллельна одной из его сторон и равна её половине:

Треугольники называются равными, если у них соответствующие стороны равны и соответствующие углы равны:

У равных треугольников все соответствующие элементы равны (стороны, углы, высоты, медианы, биссектрисы, средние линии и т.д.)

В равных треугольниках против равных сторон лежат равные углы, а против равных углов – равные стороны.

Первый признак равенства треугольников.

Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны:

Второй признак равенства треугольников.

Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны:

Третий признак равенства треугольников.

Если три стороны одного треугольника равны соответственно трём сторонам другого треугольника, то такие треугольники равны:

Подобными называются треугольники, у которых соответствующие стороны пропорциональны.

Коэффициент пропорциональности называется коэффициентом подобия:

Два треугольника подобны, если:

Два угла одного треугольника равны двум углам другого треугольника.
Две стороны одного треугольника пропорциональны двум сторонам другого, и углы, образованные этими сторонами, равны.
Стороны одного треугольника пропорциональны сторонам другого.

У подобных треугольников соответствующие углы равны, а соответствующие отрезки пропорциональны:

Отношение периметров подобных треугольников равно коэффициенту подобия.

Отношение площадей подобных треугольников равно квадрату коэффициента подобия.

Прямая, пересекающая две стороны треугольника, и параллельная третьей, отсекает треугольник, подобный данному:

Три средние линии треугольника делят его на четыре равных треугольника, подобные данному, с коэффициентом подобия ½:

Медианой треугольника называется отрезок, который соединяет вершину треугольника с серединой противолежащей стороны.

Три медианы треугольника пересекаются в одной точке, делящей медианы в отношении 2:1, считая от вершины:

Медиана делит треугольник на два равновеликих (с равными площадями) треугольника.
Три медианы треугольника делят его на шесть равновеликих треугольников:

Длины медиан, проведённых к соответствующим сторонам треугольника, равны:

Биссектрисой треугольника, проведённой из данной вершины, называется отрезок биссектрисы угла треугольника, соединяющий эту вершину с точкой на противолежащей стороне.

Биссектрисы внутренних углов треугольника пересекаются в одной точке, находящейся внутри треугольника, равноудалённой от трёх его сторон, которая является центром окружности, вписанной в данный треугольник.

Биссектриса внутреннего угла треугольника делит противолежащую углу сторону на отрезки, пропорциональные двум другим сторонам:

Длина биссектрисы угла А :

Биссектрисы внутреннего и смежного с ним внешнего угла перпендикулярны.

Биссектриса внешнего угла треугольника делит (внешне) противолежащую сторону на отрезки, пропорциональные двум другим сторонам.

BL – биссектриса угла В ;

ВЕ – биссектриса внешнего угла СВК :

Высотой треугольника называется перпендикуляр, опущенный из любой вершины треугольника на противолежащую сторону или на продолжение стороны.

Высоты треугольника пересекаются в одной точке, которая называется ортоцентром треугольника.

Высоты треугольника обратно пропорциональны его сторонам:

Длина высоты, проведённой к стороне а :

Серединный перпендикуляр – это прямая, которая проходит через середину стороны треугольника перпендикулярно к ней.

Три серединных перпендикуляра треугольника пересекаются в одной точке, которая является центром окружности, описанной около данного треугольника.

Точка пересечения биссектрисы угла треугольника с серединным перпендикуляром противолежащей стороны лежит на окружности, описанной около данного треугольника.

Окружность называется вписанной в треугольник, если она касается всех его сторон.

Точки касания вписанной окружности сторон треугольника отсекают от его сторон три пары равных между собой отрезков:

Радиус вписанной в треугольник окружности – расстояние от её центра до сторон треугольника:

Окружность называется описанной около треугольника, если она проходит через все его вершины.

Радиус описанной окружности:

Треугольник называется равнобедренным, если у него две стороны равны. Равные стороны называют боковыми сторонами, а третью – основанием равнобедренного треугольника.

В равнобедренном треугольнике углы при основании равны: ∠ A = ∠ C.

В равнобедренном треугольнике медиана, проведённая к основанию, является и биссектрисой, и высотой: BL – медиана, биссектриса, высота.

Основные формулы для равнобедренного треугольника:

Треугольник у которого все стороны равны называется равносторонним или правильным треугольником.

Центры вписанной и описанной окружностей правильного треугольника совпадают.

Все углы равностороннего треугольника равны:

Каждая медиана равностороннего треугольника совпадает с биссектрисой и высотой, которые проведены из той же вершины:

Основные соотношения для элементов равностороннего треугольника

Треугольник называется прямоугольным, если у него есть прямой угол.

Стороны, прилежащие к прямому углу, называются катетами, противолежащая прямому углу – гипотенузой.

Прямоугольные треугольники равны если у них равны:

два катета;
катет и гипотенуза;
катет и прилежащий острый угол;
катет и противолежащий острый угол;
гипотенуза и острый угол.

одному острому углу;
из пропорциональности двух катетов;
из пропорциональности катета и гипотенузы.

Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе:

Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе:

Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему:

Котангенсом острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему:

Катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу:

Высота прямоугольного треугольника, проведённая из вершины прямого угла, есть среднее пропорциональное между проекциями катетов на гипотенузу:

Высота прямоугольного треугольника, проведённая из вершины прямого угла, может быть определена через катеты и их проекции на гипотенузу:

Медиана, проведённая из вершины прямого угла, равна половине гипотенузы:

Высота прямоугольного треугольника, проведённая из вершины прямого угла, делит данный треугольник на два треугольника, подобные данному:

Площадь прямоугольного треугольника можно определить

через катеты:

через катет и острый угол:

через гипотенузу и острый угол:

Центр описанной окружности совпадает с серединой гипотенузы.

Радиус описанной окружности:

Радиус вписанной окружности:

Три окружности, каждая из которых касается одной стороны (снаружи) и продолжений двух других сторон треугольника, называются вневписанными.

Центр вневписанной окружности лежит не пересечении биссектрисы одного внутреннего угла и биссектрис внешних углов при двух других вершинах.

Так точка О₁ , центр одной из вневписанных окружностей Δ ABC , лежит на пересечении биссектрисы ∠ A треугольника ABC и биссектрис BО₁ и C О₁ внешних углов Δ ABC при вершинах B и C .

Таким образом, шесть биссектрис треугольника – три внутренние и три внешние – пересекаются по три в четырёх точках – центрах вписанной и трёх вневписанных окружностей.

Δ ABC является ортоцентричным в Δ О₁О₂О₃ (точки A , B и C – основания высот в Δ О₁О₂О₃ ).

В Δ ABC углы равны 180°–2 О₁ , 180°–2 О₂ , 180°–2 О₃ .

Радиус окружности, описанной около Δ О₁О₂О₃ , равен 2 R , где R – радиус окружности, описанной около Δ ABC .

Δ ABC имеет наименьший периметр среди всех треугольников, вписанных в Δ О₁О₂О₃ .

Если r_a , r_b , r_с – радиусы вневписанных окружностей в Δ ABC , то в Δ ABC верно:

для r –

для R –

для S –

для самих r_a , r_b , r_с –

Теорема косинусов. Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними:

если c 2 > a 2 +b 2 , то угол γ – тупой ( cos γ
если c 2 2 +b 2 , то угол γ – острый ( cos γ > 0 );
если c 2 = a 2 +b 2 , то угол γ – прямой ( cos γ = 0 ).

Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих углов. Коэффициент пропорциональности равен диаметру описанной окружности:

Читайте также: