Обновлено: 15.05.2024

Вокруг изобретателей новых цен­ностей вращается мир — неслышно вращается он.

История неевклидовой геометрии — самый замечательный пример развития Математической Идеи. Для нас эта история интересна вдвойне, т. к. ее главный участ­ник — гениальный русский математик Николай Ивано­вич Лобачевский.

Каким же образом Евклид сумел изложить геомет­рию так просто и с таким изяществом, что покорил целые поколения, а по числу изданий и читаемости его книга сравнима только с Библией?

Аксиомы должны быть достаточно простыми и соответствовать нашему опыту. А дальнейшее развитие теории состоит в доказательстве теорем, вытекающих толь­ко из заданных аксиом.

Система аксиом Евклида на протяжении более 2000 лет совершенствовалась многими авторами. В настоящее время существует много различных редакций системы аксиом евклидовой геометрии. Вот одна из них.

Аксиомы евклидовой геометрии на плоскости

Первая группа: аксиомы связи

1. Через две различные точки проходит одна и толь­ко одна прямая.

2. На каждой прямой имеются по крайней мере две различные точки.

3. Существуют три точки, не лежащие на одной прямой.

Вторая группа: аксиомы порядка

1. Если точка В лежит между точками А и С, то В лежит между С и А.

2. Из трех различных точек на прямой одна и толь­ко одна лежит между двумя другими.

3. Всякая прямая разбивает плоскость на две части таким образом, что для любого отрезка на плоскости выполняется следующее: если концы отрезка принад­лежат одной и той же части, то прямая не пересекает этот отрезок; если же концы отрезка принадлежат раз­ным частям, то прямая его пересекает.

Третья группа: аксиомы движения

1. Каждое движение сохраняет принадлежность точ­ки прямой.

2. Каждое движение сохраняет порядок точек на прямой.

3. Композиция двух движений также является движением.

4. Для каждого движения существует обратное движение.

5. Если некоторое движение оставляет на месте луч и его начало, то оно оставляет на месте каждую точку этого луча.

6. Какую бы пару точек мы ни взяли, существует движение, которое переставляет их местами.

7. Какую бы пару лучей с общим началом мы ни взяли, существует движение, которое переставляет их местами.

Четвертая группа: аксиома непрерывности (Дедекинда)

Пусть все точки прямой разбиты на два непустых класса так, что каждая точка первого класса предше­ствует каждой точке второго класса. Тогда либо в пер­вом классе существует точка, следующая за всеми ос­тальными точками первого класса, либо во втором клас­се существует точка, предшествующая всем точкам вто­рого класса.

Пятая группа: аксиома параллельности (пятый пос­тулат Евклида)

На плоскости через точку М, не лежащую на прямой А, можно провести одну и только одну прямую, парал­лельную прямой А.

Аксиома параллельности — самое знаменитое математическое предложение в истории. Ее обсуждение на протяжении 2000 лет завершилось гениальным откры­тием Лобачевского и привело к открытию неевклидовых геометрий, возникновению новых областей в математи­ке и новым взглядам на пространство и время.

Почему же так получилось? Дело в том, что, начи­ная со времен Евклида, многие математики не воспринимали аксиому параллельности именно как аксиому, а стремились ее доказать, потому что она казалась слож­нее остальных аксиом. Позже появился другой мотив. Утверждение, содержащееся в пятом постулате, стало казаться настолько соответствующим действительности и человеческому опыту, что никто из математиков до Лобачевского (кроме великого Гаусса) не сомневался в существовании доказательства.

На плоскости через точку М, не лежащую на прямой а, проходит более одной прямой, параллельной данной прямой а,

Оставив остальные аксиомы Евклида без изменения. За­тем он стал доказывать с помощью новой системы акси­ом различные теоремы в надежде получить противоре­чие. Если бы на некотором этапе рассуждений таковое оказалось, то это означало бы, что аксиома параллель­ности Лобачевского неверна, а следовательно, верна толь­ко аксиома Евклида. Но, доказав несколько десятков теорем, Лобачевский никакого противоречия не получил. И тогда он понял, что с математической точки зрения его система аксиом имеет такое же право на существование как и система аксиом Евклида. Так родилась неевклидова геометрия. Датой рождения считается 1826 год, когда Лобачевский доложил результаты своих исследо­ваний на заседании математического факультета Казан­ского университета.

Изменение всего лишь одной аксиомы привело к удивительным фактам. В новой, неевклидовой геометрии

Сумма углов любого треугольника оказалась меньше 180°, причем эта сумма зависела от площади S треугольника:

Здесь K — некоторая постоянная, определяемая выбором масштаба. Из этой формулы видно, что площадь любого треугольника не может быть более K2.

Далее, оказалось, что в геометрии Лобачевского нет подобных фигур! Например, получалась такая теорема: если у двух треугольников углы равны, то эти треуголь­ники равны. Этот удивительный факт объясняется тем, что теория подобия основана на понятии параллельности. Отменяя аксиому параллельности Евклида, мы отменя­ем и подобие.

Кроме параллельных и пересекающихся прямых, на плоскости Лобачевского существуют Расходящиеся или Сверхпараллельные прямые; помимо обычных окружно­стей, есть окружности, центр которых находится в бес­конечности, и т. д.

Лобачевский понимал, что, открыв новую геомет­рию, он должен найти ответ на некоторые вопросы. Важнейший из них такой: как новая геометрия соотно­сится с реальным миром? Лобачевский был убежден, что его геометрия — не абстрактная математическая теория, не только плод его ума, а что она отражает свойства реального пространства. Он считал, что во Все­ленной действует именно его геометрия, но люди этого не замечают, т. к. различие между евклидовой и новой геометрией проявляется только при измерении очень больших расстояний. Если же измерять небольшие фи­гуры, то результаты, полученные с помощью формул старой и новой геометрии, отличаются настолько мало, что это различие заметить практически невозможно. Точнее: чем меньше измеряемые фигуры, тем геометрия Лобачевского ближе к геометрии Евклида.

Чтобы проверить эту гипотезу, Лобачевский решил найти сумму углов треугольника, две вершины которого находятся в противоположных концах земной орбиты, а третья — на звезде Сириус. Если бы сумма углов оказа­лась меньше 180°, то гипотеза Лобачевского получила бы подтверждение.

Проведя предварительные вычисления, Лобачевский установил, что если сумма углов в этом треугольнике и окажется меньше чем 180°, то не более чем на 4 милли­онных секунды! (Секунда — 1/3600 часть градуса.) По­этому практические измерения выполнить невозможно, т. к. ни один из астрономических приборов не обладал (и до сих пор не обладает) требуемой точностью.

Другая важная проблема заключалась в необходимо­сти выяснить, не содержит ли система аксиом новой геометрии каких-либо внутренних противоречий? Ведь никто не может доказать Все теоремы, поэтому нужно как-то гарантировать, что пользуясь аксиомами, мы ни­когда не получим взаимоисключающих результатов. Лобачевский много работал над этой проблемой, но она оказалась настолько глубокой и сложной, что завершить ее удалось только через несколько десятилетий усилия­ми многих замечательных математиков.

Расстояние (в смысле геометрии Лобачевского) между точками A И В вычисляется по следующей формуле

Аналогичную формулу можно записать и для углов.

Расстояние (в смысле геометрии Лобачевского) между точками А и В вычисляется по формуле

Для вычисления углов специальная формула не нужна: на модели Пуанкаре углы в смысле геометрии Лобачев­ского — это обычные углы.

Есть и другие модели геометрии Лобачевского.

Существование моделей доказывает, что система ак­сиом Лобачевского является Непротиворечивой. Так решается одна из важнейших проблем, над которой в последние годы жизни работал сам Лобачевский.

С другой стороны, наличие моделей, или как еще говорят, Реализации геометрий Евклида и Лобачевского, закрывает проблему 2000-летней давности: можно ли Доказать аксиому параллельности, т. е. вывести ее из других аксиом? Теперь ясно, что нельзя, потому что эта аксиома Не зависит от остальных аксиом. Независи­мость вытекает из того факта, что после замены аксио­мы параллельности Евклида на аксиому параллельности Лобачевского мы вновь получаем непротиворечивую си­стему аксиом.

Переоценить значение открытия Лобачевского не­возможно. Никакой другой математический результат не имел столько значительных последствий. Благодаря открытию геометрии Лобачевского возникли новые важнейшие области математики: основания геометрии, основания математики, математическая логика. Мате­матики поняли силу аксиоматического метода и стали его широко применять во всех разделах математики и даже в физике. Далее, поскольку возник новый матема­тический объект — система аксиом — появились и спе­циальные методы его исследования, так называемая ме­таматематика. Бурно развилась теория алгоритмов, тесно связанная с математическими основами функциони­рования электронно-вычислительных устройств. В итоге было подвергнуто анализу все здание математики.

История пятого постулата показывает, как конкретная математическая идея, пройдя тысячелетия, как бы связала различные эпохи и стала одним из тех стержней, около которых вращается мир. Гениальные умы и великие мас­тера вращают наш мир, создавая настоящие ценности, и среди них математика — одна из звезд первой величины.

Ни одно из замечательных открытий в математике не остается без приложений. Совершенную теорию ко­нических сечений* создал еще греческий математик Аполлоний за 200 лет до н. э. Первое же практическое приложение этой теории было дано только в начале XVII в. величайшим астрономом Кеплером, который сформулировал один из своих законов так: Все планеты движутся по эллиптическим орбитам, в одном из фо­кусов которых находится Солнце.**

* Это эллипсы, гиперболы и параболы, которые получаются как линии пересечения кругового конуса с различными плоскостями.

** Напомним, что Эллипсом называется кривая, все точки которой обладают одним и тем же свойством: сумма расстояний от каждой точки эллипса до двух фиксированных точек, на­зываемых фокусами, есть величина постоянная, т. е. одна и та же для всех точек эллипса.

Таким образом, теория конических сечений ждала своего приложения 1800 лет.

Когда Лобачевский открыл свою геометрию, многие его современники, в том числе даже такой выдающийся математик, как Остроградский, считали неевклидову геометрию не более чем подозрительной забавой. Но уже через 50 лет появилось много неевклидовых геометрий, а через 75 лет Эйнштейн сформулировал принципы тео­рии относительности, и с этого момента неевклидовы геометрии стали рабочим инструментом физиков.

Еще меньше времени прошло от рождения матема­тической логики, которая вначале считалась сугубо формальной наукой, до того момента, когда вдруг выяс­нилось, что развитые ею методы — основа для создания будущих ЭВМ.

И таких примеров немало. Все они показывают, что на великом дереве математики зреет может быть и не так много плодов, но каждый из них, созрев, продвига­ет человечество на шаг вперед.

Проникновение геометрии в Древнюю Грецию превратило ее из эмпирической и установленной на глаз науки в цепь связанных между собой постулатов и аксиом, каждые из которых заняли определенное место в создаваемой строгой науке. Именно в Древней Греции геометрия приобрела тот современный вид, который мы помним из средней школы: каждое предположение логически вытекает из предыдущего, вместе с которым обусловливает последующее.

Нужно отметить, что, попав на благодатную почву, геометрия как наука стала бурно развиваться и даже превращаться в своеобразный культ. Каждая теорема, которую логически выводили на основании других, была маленькой победой человеческого ума, так как знания, полученные опытным путем, подтверждались строгими правилами. Ученые Древней Греции старались свести к необходимому минимуму те факты, которые устанавливают опытным путем, то есть созерцанием и наблюдением. Превратить геометрию в науку, каждое положение которой выводится по правилам логики, — вот какой была цель научной школы Платона. Согласно тенденциям этой школы любая научная дисциплина, в том числе и геометрия, должна выводиться или развиваться из как можно меньшего числа исходных положений, которые составляют костяк данной науки. Кроме этого, Платон и его последователи старались освободить изложение геометрии от наглядных выводов.

Фундаментальный и основополагающий труд Евклида состоит из тринадцати книг и предлагает значительный объем знаний — от учения о параллельных линиях до теоремы Пифагора.

• Нужно потребовать, чтобы от каждой точки к каждой другой точке можно было провести прямую линию.
• И чтобы ограниченную прямую можно было непрерывно продолжать по прямой.
• И чтобы вокруг любого центра любым радиусом можно было провести окружность.
• И чтобы все прямые углы были равны друг другу.
• И чтобы, когда прямая, пересекая две прямые, образует внутренние односторонние углы, составляющие в сумме меньше двух прямых углов, эти прямые при продолжении пересекались в точке, лежащей с той стороны, где расположены эти углы.

Геометрия Лобачевского

Разрешить проблему параллелей удалось русскому математику Николаю Ивановичу Лобачевскому. Однако доказательство было выполнено косвенно. Он просто допустил, что пятый постулат неверен, и на основании этого вывел новую (так называемую не евклидову) геометрию. Тот факт, что новая геометрия непротиворечива, удалось доказать лишь спустя тридцать лет. Отсюда следует, что проблема параллелей снимается сама собой.

Лобачевский вместо пятого постулата сформулировал новую аксиому параллельных прямых, которая по смыслу оказалась прямо противоположна пятому постулату Евклида:

Через точку вне прямой можно провести не одну прямую, не встречающуюся с данной прямой, а по крайней мере две.

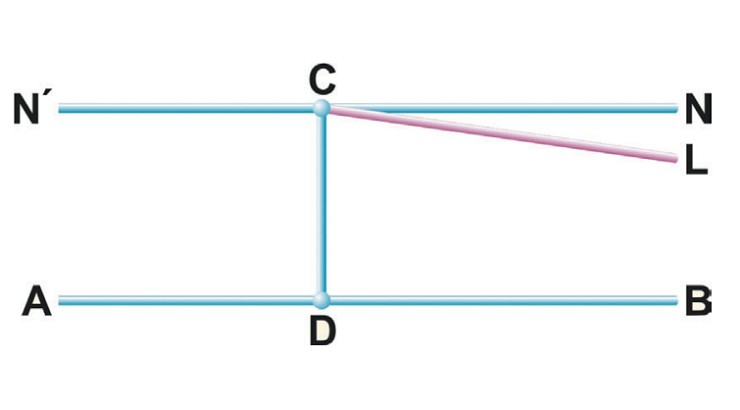
Если из точки С, расположенной вне прямой AB, опустить на прямую AB перпендикуляр СD, а затем еще к прямой CD построить перпендикуляр CN, то легко доказывается, что NN (прямая, полученная продолжением CN) будет параллельна прямой AB. Из пятого постулата Евклида следует, что из всех прямых плоскости ABC, которые проходят через точку С, только одна прямая NN не будет встречаться с прямой AB. Нам кажется это очевидным! Однако Лобачевский отказался от этого утверждения и допустил, что через точку С проходит по крайней мере еще одна прямая (например, CL), которая тоже не пересекает AB

На основании этой теоремы и остальных четырех постулатов абсолютной геометрии Лобачевский и получил свою, которая была так же логически безупречна, как и геометрия Евклида.

Аксиома Лобачевского на первый взгляд может показаться абсурдной или как минимум странной. Кажется, что он подменяет очевидное неочевидным, противоречит установившимся геометрическим представлениям. Но если этот вопрос рассмотреть глубже, то неочевидность именно пятого постулата Евклида будет налицо.

Так, если внимательно прочитать первые четыре постулата Евклида, можно заметить, что они относятся к фигурам ограниченного размера, а пятый — нет. Он оперирует неограниченной, бесконечной прямой. В итоге если мы захотим проверить правильность данного постулата на практике, то не сможем это сделать, поскольку такой эксперимент осуществить невозможно. Можно представить следующую ситуацию. Например, если предположить, что угол MCL очень маленький, а затем продлить отрезки CL и AB, то, даже обладая необширной фантазией, можно представить, что при таких условиях эти прямые не пересекутся даже на расстоянии, выходящем за пределы нашей планеты! В то же время если взять какую-либо ограниченную часть пространства, например круг, то каким бы большим он ни был, мы можем провести множество прямых, проходящих через точку С и не пересекающих прямую AB.

Поэтому нет никаких оснований считать утверждение Лобачевского неправильным.

Отличие двух противоположных по своей сути предположений заключается только в том, что евклидов постулат более понятен человеческому сознанию.

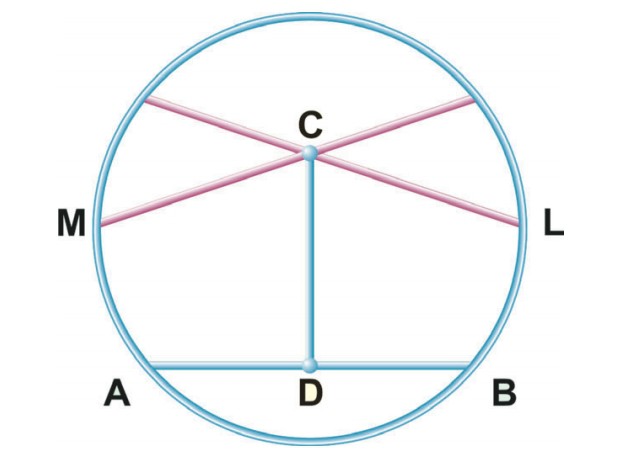
В ограниченном пространстве (круге) через точку С можно провести более одной прямой (CL и CM), не пересекающей прямую AB

Он соответствует нашему обыденному восприятию, в конце концов мы к нему привыкли… В этом случае можно вспомнить, что у древних было распространено представление, будто Земля плоская, а факт, что она круглая (как предполагала революционная гелиоцентрическая теория Коперника), полностью отрицался. Однако в отличие от теории Коперника, в которой говорилось об ином расположении и движении тел в пространстве, понимание идеи Лобачевского требует более абстрактного мышления.

Доказательства непротиворечивости геометрии Лобачевского

Не секрет, что геометрия Лобачевского не получила признания при его жизни из-за необычности. Более того, он был осмеян и к концу своих дней морально опустошен, так как считал, что теории суждено умереть вместе с создателем. Все осложнялось тем, что ученому не удалось найти объективных доказательств непротиворечивости своей теории. Для признания правоты Лобачевского потребовалось не только время, но и дальнейшее развитие математической науки, нахождение связей между различными ее разделами.

Теория Лобачевского прошла проверку временем и не оказалась пустышкой, которая, как думали его современники, в будущем сама уничтожит себя.

Фактический материал, который позволил устранить сомнения в непротиворечивости новой геометрии, был получен при разработке теории поверхностей. Если проследить за изменением свойств фигур, расположенных на изгибаемых поверхностях, то можно сделать некоторые неожиданные выводы. Сама теория поверхностей разрабатывалась немецким математиком Карлом Фридрихом Гауссом, а затем развивалась российским ученым Фердинандом Миндингом. Одним из главных понятий в теории поверхностей были так называемые геодезические линии, которые можно сравнить с обыкновенными прямыми на плоскости. И геодезические линии, и прямые выполняют одну и ту же функцию — определяют кратчайшее расстояние между точками. Разница лишь в том, что в искривленном пространстве геодезические линии представляют собой, грубо говоря, искривленные линии. Например, на сфере геодезическими линиями являются большие окружности, опоясывающие ее.

В результате Миндинг вывел формулы для геодезических треугольников (в них стороны образованы геодезическими линиями), которые совпали с планиметрией Лобачевского. Удивительно, но факт — доказательства непротиворечивости новой геометрии практически лежали на поверхности и существовали уже при жизни ученого. Однако ни один из математиков не заметил этого, так как они не были знакомы с работами друг друга. Потребовалось время, и только через 28 лет после открытия Миндинга (по прошествии 12 лет после смерти Лобачевского) итальянский геометр Эудженио Бельтрами сопоставил эти два исследования, провел строгие расчеты и вывел модель геометрии Лобачевского — три псевдосферические поверхности.

Таким образом и была убедительно доказана непротиворечивость, иными словами — верность геометрии Лобачевского. Она выражает свойства определенных криволинейных фигур в пространстве Евклида (таком, которое описывается аксиомами геометрии Евклида), а значит, не может быть противоречивой. Если бы она была таковой, то тогда геометрия Евклида противоречила бы сама себе, что не является истиной. Со временем было показано, что данная модель лишь частично доказывает непротиворечивость неевклидовой геометрии. Однако начало было положено.

Как только была доказана непротиворечивость геометрии Лобачевского, идеи на ее основе стали оказывать влияние на дальнейшее развитие математической науки.

Интересно, что вскоре была опубликована переписка Гаусса, в которой фигурировало его настоящее мнение о Лобачевском, скрываемое в годы непризнания неевклидовой геометрии. Ведь симпатия к ученому и его открытию тогда грозила всеобщим осмеянием.

Полная реабилитация Лобачевского дала импульс к появлению новых моделей неевклидовой геометрии, полностью подтверждающих непротиворечивость геометрии ученого.

Александр Фридман пришел к выводу, что Вселенная расширяется с течением времени и пространство такой Вселенной обладает геометрией Лобачевского, то есть подчиняется законам неевклидовой геометрии

Сферы применения неевклидовой геометрии Лобачевского

Лобачевский показал, что в пределах Солнечной системы для расчетов достаточно применять простую евклидову геометрию. Свою геометрию он использовал для математического анализа, а точнее — для вычисления определенных интегралов. Будучи уверенным в верности собственной теории и в том, что классическая геометрия — частный (а вернее — предельный) случай неевклидовой геометрии, ученый был убежден, что его система имеет гораздо больший потенциал: она не может не описывать более глобальные закономерности природы.

После того как непротиворечивость геометрии Лобачевского была доказана, на нее обратили внимание самые выдающиеся математики того времени. В 1881-м на ее основе была создана новая дисциплина — теория автоморфных функций, построенная великим французским математиком и физиком Анри Пуанкаре, которая имеет огромное значение для фундаментальной науки.

Важное практическое приложение геометрии Лобачевского нашел русский физик Александр Фридман. Используя в 1922 году идеи теории относительности и решая уравнение Эйнштейна, он пришел к выводу, что Вселенная расширяется с течением времени.

Медаль 1895 года, выдававшаяся в Казанском императорском университете рецензентам работ, представленных на соискание премии им. Н. И. Лобачевского

Следующим важным применением геометрии Лобачевского является то, что она оказалась естественной частью теории относительности.

Законы сложения относительных скоростей, полученные Альбертом Эйнштейном, напрямую связаны с геометрией Лобачевского.

Прошение Л. Н. Толстого о приеме в Казанский императорский университет, написанное на имя ректора Н. И. Лобачевского, при котором учебное заведение переживало свои лучшие времена. В нем читали лекции самые лучшие преподаватели, в него стремились лучшие абитуриенты

А в 1950-х годах советский физик Н. А. Черников стал успешно использовать геометрию Лобачевского для исследования столкновений элементарных частиц в ускорителе, а также при изучении других вопросов физики элементарных частиц и ядерных реакций.

Все идеи, которые были выдвинуты на основании геометрии Лобачевского, описать практически невозможно. Многие еще только находятся на пути развития, и до их практического применения остается еще много времени. Однако сама фундаментальность открытия дает полную уверенность в том, что неевклидова геометрия будет приводить к новым изобретениям, так как потенциал ее безграничен.

Краткая биография

Любая теория современной науки считается единственно верной, пока не создана следующая. Это своеобразная аксиома развития науки.

Участь эта не обошла и геометрию. Традиционная Евклидова геометрия переросла в неевклидову, геометрию Лобачевского. Именно этому разделу математики, его истории и особенностям и посвящен этот проект.

История геометрии.

Считается, что геометрия началась в так называемой Ионийской школе. Её основателем считается Фалес Милетский (640-540 (546?) гг. до н. э.). Он считался одним из семи мудрецов Греции, первым математиком, астрономом и философом. Он доказал, что углы при основании равнобедренного треугольника равны, что вертикальные углы равны, что диаметр делит окружность пополам и ещё множество теорем. Предсказание затмения солнца в 585 году также приписывается ему.

Огромный импульс развития этой школе дал Пифагор (569-470 гг. до н. э.). В основном о его личных качествах пишут то же самое, что и о Фалесе. Но к этому ещё можно добавить титул чемпиона по боксу на олимпийских играх – звание, среди математиков редкое.

1. Разделить угол на три части (задача о трисекции угла).

2. Построить квадрат, равный по площади данному кругу (задача о квадратуре круга).

3. Построить куб, равный по объему данному (задача об удвоении куба).

Нерешаемость этих задач была доказана только в 19 веке, но перед этим они успели вызвать настоящую бурю: например, задача №2 вызвала появление интегрального исчисления.

Метод доказательства от противного – тоже его заслуга. Он же сформулировал пять постулатов геометрии:

1. Через два точки можно провести одну и только одну прямую.

2. Прямая продолжается бесконечно.

3. Из любого центра можно провести окружность любым радиусом.

4. Все прямые углы равны между собой.

Пятый постулат является своеобразным философским камнем геометрии и будет подробнее описан в шестой части.

Биография Николая Ивановича

Лобачевского.

1729 – 1856

Лобачевский пользовался уважением и любовью студентов и коллег. Когда упразднили должность директора университета, то его кандидатуру на пост главного ректора утвердили без возражений. Не высказался даже его главный соперник – Симонов.

в 1842 году, во время большого пожара в Казани он героически спас древние книги, до этого, во время эпидемии холеры, превратил университет в мини-госпиталь – из-за чего умерло гораздо меньше студентов, чем в других ВУЗ’ах.

Когда негде было разместить второй класс Казанской гимназии, он предложил свой дом, обещав потом построить для гимназии дворец. Понятно, что в 1845 году он получил должность управляющего Казанским учебным округом, а после стал член-кореспондентом Гуттенгенского университета.

Но жизнь нанесла ещё один удар: он начал слепнуть. Он начал играть со своей женой в страшную игру, пытаясь убедить её, что ещё хорошо видит. Она закатывала истерики, уговаривала лечиться, но все тщетно – Лобачевский ослеп. Но, тем не менее, он продолжал преподавать и пользоваться безграничной любовью и уважением учеников. Знаменателен случай, когда молодого студента, засмеявшегося над споткнувшимся Лобачевским, однокурсники заставили уйти из университета. Лобачевский об этом даже не узнал.

Ему поставлен памятник – и поэт В. Фирсов написал о нем:

Высокий лоб, нахмуренные брови,

В холодной бронзе – отраженный луг…

Но даже неподвижный и суровый,

Он, как живой, - спокоен и могуч.

Когда – то здесь, на площади широкой,

Задумчивый, неторопливый, строгий,

Он шел на лекции – великий и живой.

Пусть новых линий не начертят руки,

Он здесь стоит, взнесенный высоко,

Как утверждение бессмертья своего,

Как вечный символ торжества науки.
Другие авторы.

Тога Гаусс написал Фаркашу Больяи то, что тот сам говорил сыну: время для этих выкладок ещё не пришло. Януш же посчитал, что Гаусс решил присвоить его труд. Но Гаусс не публиковал его – ведь он был королем математики того периода, и боялся, что его сочтут свихнувшимся.

Гаусс в то время хотел уехать – куда-нибудь далеко, где никто не помешает. Он думал о Петербурге или Казани. Но из-за бюрократии российских чиновников поездка расстроилась.

Через шесть лет Гаусс все ещё думает о Лобачевском. Но он понимает, что слишком стар, чтобы защищать новые идеи. А Лобачевский погибал без поддержки.

За год до этого, зимой 1848 года, к Гауссу пришел студент. Его звали Бернард Риман. Но Гаусс оттолкнул его. Тогда Риман, сжав зубы, уехал в Берлин. Но мир тесен, и, защитив докторскую диссертацию, он решает стать профессором. Удивительно, но тему пробной лекции утверждает и принимает именно Гаусс.

Риман создал геометрию, где прямые замкнуты, где нет параллельных прямых, а сумма углов треугольника больше 180 о . Она похожа на геометрию сферы Гаусса.

Краткое описание геометрии Лобачевского.

Иногда говорят, что в геометрии Лобачевского параллельные прямые пересекаются в бесконечности. Но это не совсем так. Есть только немного другое свойство параллельности: через одну точку вне прямой можно провести бесконечно много прямых, параллельных данной. Это видно на рисунке 1. Причем параллельность сохраняется только в сторону уменьшения расстояния между прямыми. Этот, казалось бы, простой факт, меняет всю геометрию. Как, например, в геометрии Евклида доказывается, что сумма углов треугольника равна 180 о ? Классическое доказательство приведено на рисунке 2. Используется свойство углов при накрест лежащих прямых, и выходит, что Ð1+Ð2+Ð3=180 о . Но так как в геометрии Лобачевского параллельность сохраняется только в одном направлении, то для нахождения суммы углов треугольника*, то нужно провести две прямые, параллельные данной в разные стороны. Что получается, видно на рисунке 3. Понятно, что теперь сумма углов треугольника меньше 180 о . Эта разница была названа Лобачевским дефектом треугольника.

Одними из важных объектов на плоскости Лобачевского являются пучки прямых. Но чтобы описать эти пучки, сначала надо уяснить, что в плоскости Лобачевского есть три типа расположения прямых: прямые или параллельны, или пересекаются, или являются расходящимися.
_______

* Здесь и далее подразумевается геометрия Лобачевского, если нет оговорки на геометрию Евклида.

Так вот, первый вид пучков образован прямыми, имеющими общую точку – центр пучка (рис. 4а). Пучок расходящихся прямых – это перпендикуляры к одной прямой – оси пучка (рис. 4б). Из этого определения выходит интересное и, казалось бы, абсурдное утверждение, что два перпендикуляра к одной прямой непараллельны, и отличие от геометрии Евклида.

И, наконец, пучок, образуемый прямыми, параллельными данной прямой в заданном направлении (рис. 4в).

Следующими объектами геометрии Лобачевского являются кривые. Для их построения Лобачевским было введено понятие соответственных точек. В пучке первого рода это точки на прямых, равноудаленные от центра (рис. 5а). В пучке второго рода это точки прямых, лежащие по одну сторону от оси и отстоящие от нее на одинаковые расстояния (рис. 5б). Наконец, в пучке третьего рода они расположены симметрично относительно биссектрисы полосы между двумя прямыми, на которых лежа эти точки (рис. 5в).

Соединив соответствующие точки первого пучка, мы получим окружность. В случае второго пучка мы получаем линию равных расстояний, а в третьем случае – так называемую предельную линию.

Примеры таких построений – на рисунке 6.

Из определения предельных линий выходит, что она бесконечна. Поэтому в теоремах используется понятие предельной дуги, или дуги предельной линии.

Для концентрических предельных дуг существуют несколько правил: во-первых, равным хордам соответствуют равные дуги, большей хорде – большая дуга; отрезки осей, заключенные между дугами, равны, и отношение двух предельных дуг, заключенных между одинаковыми осями, зависит только от расстояния. Причем это отношение при S₁ >S₂ равно , где х – расстояние, а к – некотрая константа. Сам Лобачевский дает её определение так: к – это расстояние между двумя предельными дугами, заключенными между двумя осями, отношение которых равно е . Физический смысл этой константы заключается в отображении кривизны пространства Лобачевского.

Лобачевским была создана и стереометрия. Прямые в пространстве могут или скрещиваться, или лежать в одной плоскости. Скрещивающиеся прямые имеют смысл двух прямых, имеющих общий перпендикуляр, определяющий кратчайшее расстояние между ними. У параллельных прямых есть два основных свойства: во-первых, если через две параллельные прямые провести две пересекающиеся плоскости, то прямая пересечения плоскостей будет параллельна двум другим; во-вторых, две прямые, параллельные третей, параллельны одна другой в том же направлении – даже если третья прямая не лежит в плоскости первых двух.

Для анализа расположения прямой и плоскости, на плоскость опускается проекция. Если прямая и плоскость параллельны, то прямая и её проекция на плоскость тоже параллельны, и наоборот. Так же определяется и расположение двух плоскостей – с тем лишь отличием, что, если нельзя провести плоскость, перпендикулярную двум выбранным плоскостям и проходящую через выбранную прямую и её проекцию, то плоскости обязательно пересекутся.

Аналогию пучкам в пространстве составляют связки. Связки также делятся на три рода: первые образуются прямыми и плоскостями, проходящими через одну точку – центр связки; вторые образованны прямыми и плоскостями, перпендикулярными некой плоскости; и, наконец, третьи образованы прямыми и плоскостями, параллельными данной плоскости в одном направлении. Точно так же определяются соответствующие точки. В случае связки первого рода они формируют сферу, второго – поверхность равных расстояний, третьего – предельную поверхность. Предельная поверхность обладает удивительным свойством: на ней справедлива геометрия Евклида. Этот факт свидетельствует о том, что неевклидова геометрия не опровергает евклидову, а включает её в себя как органичную часть.

В процессе нахождения тригенометрических формул, Лобачевский проецировал прямоугольный треугольник с предельной плоскости на плоскость, касательную к ней. Пользуясь формулами и , вывод которых приведен в приложении, он получил тригинометрические формулы своего пространства. Соотношения в прямоугольном треугольнике при этом остаются одинаковыми, но cos , sin и tg определяются по-другому: , , , где с – сторона против прямого угла, а – против a , в – противb .

Несмотря на все кажущиеся странности, геометрия Лобачевского является настоящей геометрией нашего мира, и Евклидова является только её составной частью. Но в пределах ежедневных измерений Евклидова геометрия дает исчезающе малые ошибки, и мы пользуемся именно ею.

5 постулат.

Конечно, ещё сам Евклид пытался вывести этот сложный постулат из более простых. После него этой проблемой занимались почти все известные математики, но чаще всего это заканчивалось тем, что постулат выводился только при принятии каких-то дополнительных предположений. У менее удачливых математиков не получалось вообще ничего.

Самую известную попытку доказать пятый постулат методом от противного предпринял итальянский монах Джироламо Саккерти в 1733 году. Но отрицание пятого постулата – это и есть главное отличие геометрии Лобачевского от геометрии Евклида. Он, как и другой математик И. Г. Ламберт в 1766 году, вплотную подошел к неевклидовой геометрии, но не нашел её реальной.

Гаусс, изучая поверхности, обнаружил, что на поверхностях отрицательной кривизны сумма углов треугольника меньше 180 о . Он был в шаге от опровержения пятого постулата.

Попыток было много – и именно недоказуемость этого предположения привела к открытию неевклидовой геометрии.

Геометрия Лобачевского в реальном мире.

Если геометрия Евклида является только частью геометрии Лобачевского, то выходит, что наш мир – не мир Евклида, как принято считать? Почему же мы не замечаем разницы?

Как пример можно привести тот факт, что видимый звездный свод это ни что иное, как предельная плоскость. Астрономам после признания достижений Лобачевского пришлось пересчитывать все расстояния между звездами – и ошибки достигали 1/6.

История возникновения неевклидовой геометрии. Основные понятия Лобачевского о пространственных структурных отношениях и их обобщение, области применения. Нахождение моделей плоскости и протяженности. Аксиома о параллельных прямых и уравнение сферы.

Рубрика	Математика
Вид	реферат
Язык	русский
Дата добавления	04.09.2014
Размер файла	1,5 M

Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.

на тему: Неевклидова геометрия, геометрия Лобачевского, Риманова геометрия

1. История возникновения неевклидовой геометрии

Но никто не сомневался в истинности постулатов Евклида, что касается и V постулата. Между тем уже в древности именно постулат о параллельных привлек к себе особое внимание ряда геометров, считавших неестественным помещение его среди постулатов. Вероятно, это было связано с относительно меньшей очевидностью и наглядностью V постулата: в неявном виде он предполагает достижимость любых, как угодно далеких частей плоскости, выражая свойство, которое обнаруживается только при бесконечном продолжении прямых.

Сам Евклид и многие ученые пытались доказать постулат о параллельных. Одни старались доказать постулат о параллельных, применяя только другие постулаты и те теоремы, которые можно вывести из последних, не используя сам V постулат. Все такие попытки оказались неудачными. Их общий недостаток в том, что в доказательстве неявно применялось какое-нибудь предположение, равносильное доказываемому постулату. Другие предлагали по-новому определить параллельные прямые или же заменить V постулат каким-либо, по их мнению, более очевидным предложением. [3]

Но многовековые попытки доказательства пятого постулата Евклида привели, в конце концов, к появлению новой геометрии, отличающейся тем, что в ней V постулат не выполняется. Эта геометрия теперь называется неевклидовой.

Независимо от Лобачевского, существование новой геометрии установили великий немецкий математик Карл Фридрих Гаусс и замечательный венгерский математик Янош Бойяи, сын Фаркаша Бойяи. Названные три автора первоначально шли тем путем, который указан выше. Стремясь доказать V постулат от противного, они глубоко развили аксиоматическую систему, получающуюся при отрицании истинности V постулата, но не обнаружили при этом никаких противоречий. Однако, в противоположность своим предшественникам, эти три великих математика сделали из полученных ими результатов вывод о существовании геометрической системы, отличной от евклидовой. При этом они продолжали исследовать новую геометрию, получая дальнейшие относящиеся к ней теоремы.

Огромное впечатление, произведённое на умы математиков открытием Лобачевского, Бойяи и Гаусса, быть может, было бы несколько менее сильным, если бы люди заметили, что ещё задолго до Лобачевского они фактически уже владели содержательной геометрической схемой, отличной от традиционной геометрии Евклида, т.е. уже знали одну из неевклидовых геометрий. Однако твёрдое убеждение всех учёных в универсальности системы Евклида не позволило им оценить по достоинству тот запас знаний, которым они располагали. Именно поэтому первым примером геометрической системы, отличной от классической геометрии Евклида, считается обычно неевклидова геометрия Лобачевского. Значительно же более простая схема, по существу разработанная с большими деталями за много веков до Лобачевского, связывается обычно с именем гениального немецкого математика Бернхарда Римана, впервые обратившего внимание на родство этой схемы с классической геометрией Евклида и неевклидовой геометрией Лобачевского. Риман целиком пересмотрел основы геометрии Евклида, вместо них предложил свои собственные принципы построения геометрии, исходя из весьма общих соображений.[19]

Таким образом, основным пунктом, откуда начинается разделение геометрии на обычную евклидову (употребительную) и неевклидову (воображаемую геометрию) является, как известно, постулат о параллельных линиях. Плоскость Лобачевского -- это плоскость (множество точек), в которой определены прямые линии, а также движения фигур (вместе с тем -- расстояния, углы), подчиняющиеся всем аксиомам евклидовой геометрии, за исключением аксиомы о параллельных, которая заменяется указанной выше аксиомой Лобачевского. Сходным образом определяется пространство Лобачевского. Задача выяснения реального смысла геометрии Лобачевского состояла в нахождении моделей плоскости и пространства Лобачевского, т. е. в нахождении таких объектов, в которых реализовались бы соответствующим образом истолкованные положения планиметрии и стереометрии геометрии Лобачевского. [5]

2. Геометрия Лобачевского

2.1 Основные понятия геометрии Лобачевского

Лобачевский определяет основные понятия геометрии, не зависящие от V постулата, и, заметив, что сумма углов прямолинейного треугольника не может быть , как это имеет место у сферических треугольников, он заявляет: “Мы видели, что сумма углов прямолинейного треугольника не может быть . Остается предполагать эту сумму или . То и другое может быть принято без всякого противоречия впоследствии, от чего и происходят две Геометрии: одна, употребительная доныне по своей простоте, соглашается со всеми измерениями на самом деле; другая, воображаемая, более общая и потому затруднительная в своих вычислениях, допускает возможность зависимости линий от углов”.

Лобачевский указывает, что в “воображаемой геометрии” сумма углов треугольника всегдаи две прямые могут не пересекаться в случае, когда они образуют с секущей углы, в сумме меньшие . Параллельные прямые определяются как такие, которые не пересекаются, но могут быть получены предельным переходом из пересекающихся. Через каждую точку плоскости проходят две прямые, параллельные данной прямой, лежащей в этой плоскости; эти прямые делят пучок прямых, проходящих через данную точку, на четыре области, в двух из которых проходят прямые, пересекающие данную прямую, а в двух - прямые, которые не пересекают эту прямую и не могут быть получены предельным переходом из пересекающихся - такие прямые называются расходящимися; параллельные прямые разграничивают пресекающие прямые от расходящихся (на рис.1 условно изображены прямые и , проведенные через точку А параллельно прямой , прямые и , проведенные через точку А и пресекающие прямую , и прямые и , расходящиеся с прямой )

Рисунок 1._ Аксиома Лобачевского о параллельных прямых

Угол между прямой, проведенной через точку А параллельно прямой p, и перпендикуляром, опущенным из А на p, Лобачевский называет “углом параллельности” и показывает, что функция, выражающая зависимость этого угла от длины перпендикуляра, может быть (в современных обозначениях) записана в виде:

где q - некоторая постоянная. При угол параллельности всегда острый, причем он стремится к при, постоянная же q может служить на плоскости Лобачевского абсолютной единицей длины, аналогичной абсолютной единицей длины, аналогичной единице угла в евклидовом пространстве. Лобачевский устанавливает также, что расходящиеся прямые обладают общим перпендикуляром и удаляются друг от друга по обе стороны от него, а две параллельные прямые приближаются друг к другу и расстояния точек одной из них от другой стремится к 0 при неограниченном удалении этих точек. Сумма углов треугольника в геометрии Лобачевского всегда меньше , и если - “угловой дефект” треугольника, то есть разность между и суммой его углов, то площадь треугольника S равна:

где q - та же постоянная, что и в формуле (1).

Далее рассмотрим тот факт, что в геометрии Лобачевского, круг при стремлении его радиуса к бесконечности, переходит не в прямую, а в особого рода кривую “предельного круга” - в настоящее время такие кривые называют орициклами. Сфера при тех же обстоятельствах переходит не в плоскость, а в кривую поверхность, которую Лобачевский назвал “предельной сферой”, а в настоящее время именуют орисферой. Лобачевский отмечает, что на орисфере имеет место евклидова геометрия, причем роль прямых на ней играют орициклы. Это позволяет Лобачевскому, опираясь на евклидову тригонометрию на орисфере, вывести тригонометрию на плоскости в его геометрической системе. Название “воображаемая геометрия” подчеркивает, что эта геометрия относится к евклидовой, “употребительной”, по терминологии Лобачевского, как мнимые числа, “воображаемые”.

Лобачевский сразу же поставил вопрос об экспериментальной проверке того, какая геометрия имеет место в реальном мире - “употребительная” или “воображаемая”, для чего он решил измерить сумму углов треугольника, образованного двумя диаметрально противоположными положениями Земли на ее орбите и Сириусом и, считая один из углов этого треугольника прямым, а другой - равным углу параллельности, Лобачевский нашел, что эта сумма отличается от на разность, меньшую ошибки угломерных инструментов в его время. “После того, - пишет Лобачевский, - можно вообразить, сколько эта разность, на которой основана наша теория параллельных, оправдывает точность всех вычислений обыкновенной геометрии и дозволяет принятые начала рассматривать как бы строго доказанными”.

Это объясняет, что под “строгим доказательством теоремы о параллельных” в докладе 1826 г. Лобачевский понимал невозможность установить экспериментальным путем, какая из двух геометрий имеет место в реальном мире, откуда вытекает, что на практике можно пользоваться “употребительной геометрией”, не рискуя впасть в ошибку.

Наиболее полно изложена система Лобачевского в его “Новых началах с полной теорией параллельных” (1835-1838). Изложение геометрии у Лобачевского основывается на чисто топологических свойствах прикосновения и сечения, конгруэнтность тел и равенство отрезков определяются по существу с помощью движения.

В позднейших работах Лобачевский ввел координаты и вычислил из геометрических соображений целый ряд новых определенных интегралов, которым он специально посвятил работу[13].

2.2 Непротиворечивость геометрии Лобачевского

Выведя уже в своей первой работе “О началах геометрии” формулы тригонометрии своей новой системы, Лобачевский заметил, что “эти уравнения переменяются в… (уравнения) сферической Тригонометрии, как скоро вместо боков . b, c ставим в ??-1, b-1, c-1, но в обыкновенной Геометрии и сферической Тригонометрии везде входят одни содержания (т.е. отношения) линий: следовательно, обыкновенная Геометрия, Тригонометрия и эта новая геометрия всегда будут согласованы между собой”. Это означает, что если мы запишем теорему косинусов, теорему синусов и двойственную теорему косинусов сферической тригонометрии для сферы радиуса r в виде:

то формулы тригонометрии Лобачевского можно записать в том же виде, заменив стороны . b, c треугольника произведениями ??i, bi, ci; так как умножение сторон a, b, c на i равносильно умножению на i радиуса сферы, то, полагая r=qi и воспользовавшись известными соотношениями:

cos(ix) = ch x, sin(ix) = ish x, (6)

мы можем переписать соответственные формулы тригонометрии Лобачевского в виде:

Читайте также:

  
• Проблема зарождения науки и специфика протонауки доклад
  
• Франция долгий путь к единству 6 класс доклад
  
• Мышление доклад по биологии
  
• Методы формирования сознания личности педагогика доклад
  
• Личность и агрессия доклад