Числа фибоначчи и золотое сечение доклад

Обновлено: 02.07.2024

Предисловие.

Кроме того, и это являются фундаментальным фактом истории математики нашего времени, существенно сместился центр математических исследований в целом. В частности, утратила свои доминирующие позиции теория чисел и резко повысился удельный вес экстремальных задач. В самостоятельную отрасль математики сложилась теория игр. По существу возникла вычислительная математика.

Глава 1: Числа Фибоначчи и их свойства.

Введение.

Из выше приведенной задачи становится ясно, что Фибоначчи вывел особый ряд чисел. Примечательно, что первые два члена этой последовательности равны 1, следующее же члены равны сумме двух предыдущих.

2.Перейдем от кроликов к числам рассмотрим следующею числовую последовательность:

в которой каждый член равен сумме двух предыдущих членов, т.е. при всяком n>2

Такие последовательности, в которых каждый член определяется, как некоторая функция предыдущих в математике называется рекуррентными или по-русски, возвратными последовательностями. Сам процесс последовательного определения элементов таких последовательностей называется рекуррентным процессом, а равенство(2) – возвратным (рекуррентным) уравнением. Число рекуррентно – индуктивно по его номеру.

Заметим, прежде всего, что по одному этому условию (2) члены последовательности (1) вычислять нельзя.

Можно составить сколько угодно различных числовых последовательностей, удовлетворяющих этому условию; например,

значит для однозначного построения последовательности (1) условия (2) явно недостаточно, и нам следует указать некоторые дополнительные условия. Например, мы можем задать несколько первых членов последовательности (1). Сколько первых членов последовательности (1) мы должны задать, чтобы можно было вычислить все следующие члены, пользуясь при этом только условием (2)?

Начнем с того, что не всякий член последовательности может быть получен при помощи (2) уже хотя бы потому, что не у каждого члена (1) имеется два предшествующих; например. Перед первым членом последовательности вообще не стоит ни одного члена, а перед вторым её членом стоит только один, значит вместе с условием (2) для определения последовательности (1) знать два ее первых члена необходимо.

3.Обратимся теперь к важному частному случаю последовательности (1), когда u 1 =1 и u 2 =1. Условие (2). как было отмечено, дает нам возможность вычислять последовательно один за другим все члены этого ряда. Нетрудно проверить, что в этом случае первыми четырнадцатью его членами будут числа

которые уже встречались в задаче о кроликах.

В честь автора этой задачи вся последовательность(1) при u 1 =u 2 =1 называется рядом Фибоначчи , а члены её – числами Фибоначчи.

Также в этом труде содержалось множество других задач. Л. Фибоначчи неоднократно путешествовал по странам Востока и в своей книге использовал труды арабских математиков.

1.Разделим отрезок АВ единичной длины на две части так, чтобы большая из его частей являлась средним пропорциональным между меньшей его частью и всем отрезком.

Обозначим для этого искомую длину большей части отрезка через х. Очевидно, длина его меньшей части при этом будет равна 1-х, и условие нашей задачи дает нам пропорцию

откуда х 2 =1-х (1.2)

положительным корнем(1.1) являются _-1_+_√_5_

так что отношения в пропорции (1.1) равны

_1_ = ___2___ = ___2(1+√5)__ = _1+√5_ = а

каждое такое деление (точкой С 1 ) называется делением в среднем и крайнем отношении . Его часто называют также золотым делением или золотым пропорцией (сечением).

Если взять отрицательный корень этого уравнения, то делящая точка С 2 окажется вне отрезка АВ (такое деление в геометрии называется внешним делением ). Как это видно на рисунке. Легко показать, что и здесь мы имеем дело с золотым сечением:

_С 2 В_ = _А В_ = а

2.Фактическое построение точки, делящей отрезок золотым сечение, осуществляется без труда.

Пусть АВ=1; востановим из точки перпендикуляр и возьмем точку Е, для которой АЕ=1/2 (рис. 3). Тогда ЕВ = √ 1+(1/2) 2 = √5/2.

Проведя из Е, как из центра дугу через А до пересечения с ЕВ в точке D, мы получаем

Наконец проведя через D дугу с центром в В, мы находим искомую точку С 1 .точку внешнего деления С 2 можно найти из условия АС 2 = ВС 1 .

3.Золотое сечение довольно часто встречается в геометрии, например, для квадрата, вписанного в полукруг (см. рис. 4), точка С делит золотым сечением отрезок АВ.

Сторона правильного десятиугольника (рис.5) вписанного в круг радиуса R, как известно равна

2R sin 360°/2,10 т.е. 2R sin 18°

а 10 =2R _√5-1_ = R _√5-1_ = _R_

ными словами а 10 равно большей части радиуса круга, разделенного золотым сечением.

4.Рассмотрим правильный пятиугольник. Его диагонали образуют правильный звездчатый пятиугольник (рис. 6).Точка С делит отрезок АD золотым сечением.

Золотая пропорция просматривается и в других геометрических фигурах.

6.Природа дает нам многочисленные примеры расположения однородных предметов, описываемых числами Фибоначчи. В разнообразных спиралевидных расположениях мелких частей мелких частей растений обычно можно усмотреть два семейства спиралей. В одном из этих семейств спирали завиваются по часовой стрелке, а в другом против. Числа спиралей того и другого типов часто оказываются соседними числами Фибоначчи.

Так взяв молодую сосновую веточку, легко заметить, что хвоинки образуют две спирали, идущие слева снизу направо вверх.

На многих шишках семена расположены в трех спиралях, полого навивающихся на стержень шишки. Они же расположены в пяти спиралях, круто навивающихся в противоположном направлении. В крупных шишках удается наблюдать 5 и 8 и даже 8 и 13 спиралей. Хорошо заметны такие спирали и на ананасе: обычно их бывает 8 и 13.

У многих сложноцветных (например, у маргаритки или ромашки) заметно спиральное расположение отдельных цветков в соцветиях-корзинках. Число спиралей бывает здесь 13 в одном направлении и 21 в другом или даже соответственно 21 и 34. Особенно много спиралей можно наблюдать в расположении семечек крупного подсолнуха. Их число в каждом из направлений может достигать собственно 55 и 89.

Про то, как первозданная и необузданная природа функционирует и развивается по математическим законам, описанными числами Фибоначчи, мы попробуем разобраться в следующей главе.

Золотое сечение гармоническая пропорция

. . Ясно одно: Золотое Сечение и числа Фибоначчи отражают некоторые фундаментальные закономерности живой природы. А теперь . открытии, устанавливающим связь генетического кода с числами Фибоначчи и Золотым Сечением. В 1990 г. французский исследователь .

Теория чисел Фибоначчи

. золотое сечение), живое поныне, а много раньше, в 1202 г., открытием ряда Фибоначчи было обнажено фундаментальное свойство золотого сечения . – подход к определению золотого сечения. Через золотое сечение числа Фибоначчи проявляют свои свойства в .

Тайны Золотого Сечения

. на Золотом сечении и математических закономерностях, которые определяют также строение Вселенной и всего живого на . теории чисел и теории измерения. С Золотым сечением также связаны числа Фибоначчи, открытые в ХIII веке итальянским .

Божественная пропорция

. такое золотое сечение? Какова его связь с рядом Фибоначчи? 2) Выяснение общих закономерностей развития живой и неживой . частей, формирующих конические раковины, отвечает числам Фибоначчи. Так, раковины фораминифер имеют 13 .

Геометрические символы

Актуальность исследования. На мой взгляд в настоящие дни уделяется мало внимания математическим теоремам и фактам, известным из истории развития науки. На примере чисел Фибоначчи я хотел бы показать насколько они могут глобальны и широко применимы не только в математике, но и в повседневной жизни.

Целью моей работы является изучение истории, свойств, применения и связей чисел Фибоначчи с золотым сечением.

Глава 1. Числа Фибоначчи и их история.

[1]

Мы можем обозначить кол-во кроликов в любой из двенадцати месяцев как u_n. Мы получаем ряд чисел:

В ряде этих чисел каждый член равен сумме двух предыдущих. Получается, что любой член уравнения можно определить по уравнению:

Рассмотрим важный частный случай для этого уравнения, когда u₁ и u₂ =1. Мы получим последовательность чисел 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377… Эту же последовательность чисел мы получали в задачу про кроликов. Эти числа названы числами Фибоначчи в честь автора.

Эти числа а также уравнение (2) обладает многими свойствами, который будут рассматриваться в моей работе.

Глава 2. Связь между рядом Чисел Фибоначчи и прогрессиями. Основные свойства ряда.

Для того, чтобы вывести основные свойства ряда возьмем как пример первые пять чисел: 1, 1, 2, 3, 5, 8. Мы видим, что каждое новое число равно сумме двух предыдущих. Отсюда мы можем вывести формулу получения любого числа ряда, а также формулу суммы любого кол-ва чисел из ряда.

Мы видим, что формулы кардинально отличаются от формул свойственных арифметической и геометрической прогрессий. А также мы можем сказать что только первые два числа из ряда могут относится к каким либо прогрессиям.

У арифметической и геометрических прогрессий имеются только две ранее упомянутые формулы, и чтобы посчитать например сумму четных, нечетных или сумму квадратов чисел каждый раз приходится решать задачу для отдельно взятого ряда. Но так как ряд чисел Фибоначчи является неизменным (не имеет шагов, знаменателей и различных первых членов прогрессии), то это значит, что для него можно вывести формулу получения сумм отдельных элементов ряда. Вот например формула для получения суммы чисел ряда под четными номерами:

Существует аналогичная формула для чисел из ряда под нечетными номерами:

Также есть формула для получения суммы чисел из ряда возведенных в квадрат:

Глава 3. Золотое сечение и числа Фибоначчи.

Золотое сечение (золотая пропорция, деление в крайнем и среднем отношении) — деление непрерывной величины на две части в таком отношении, при котором меньшая часть так относится к большей, как большая ко всей величине. [10]

Попробуем объяснить это на примере бесконечной прямой. Примем всю прямую с за единицу. Разделим ее на две части a и b, которые делят прямую на отрезки равный по отношению к 1, как 0.618 и 0.382 соответственно. А эти числа являются одними из коэффициентов ряда чисел Фибоначчи. Мы получаем, что отношение больших частей этой прямой к меньшим асимптотически приближается к числу .

Существует две основные фигуры, в которых отражается принцип золотого сечения.

Золотое сечение было известно еще древним грекам. Архимед считается открывателем Архимедовой спирали. Её смысл состоит в том, что каждый новый завиток увеличивается в определенное число, и отношение этих завитков равно числу .

Вторая фигура – золотой треугольник. Это равнобедренный треугольник, в котором отношение боковых сторон к основанию равно . На его основе построены такие фигуры как пентаграмма и пятиконечная звезда.

Многие ученые и поэты обращали на то, что многое в природе напоминает спирали. Это действительно так. Строение раковины полностью совпадает с архимедовой спиралью.

Паук строит свою паутину спиралевидно, бивни мамонтов и рога многих животных строятся на основе архимедовой спирали.

Ботаники совместно с математиками долгое время изучали строение растений и их плодов. Они пришли к интересным выводам. Оказывается, что стебли и листья всех растений растут импульсивно по принципу уменьшения в пропорции золотого сечения. Если весь стебель обозначить за 100, то первый этап роста будет равен 62, второй – 38, третий – 24.

На самом деле строение нашего тела тоже можно рассмотреть относительно золотой пропорции. Любую часть нашего тела можно разделить также как и бесконечную прямую в начале этой главы.

Также было установлено, что молекулу нашей ДНК составляют две спирали “сноскавикипедия”длиной 34 ангстрема и шириной 21 ангстрем.[11] А так как это числа ряда Фибоначчи, их отношение равно золотой пропорции.

Золотое сечение является основополагающим и в строении галактик.

Например, даже млечный путь выстроен по принципу Архимедовой спирали.

Золотое сечение также широко распространено в искусстве и архитектуре.

Особенно это ярко выраженно в картинах Леонардо Да Винчи.

Пирамида в Гизе, которая является одной большой математической головоломкой, тоже содержит в себе золотой принцип: Длина ребра основания пирамиды в Гизе равна 783.3 фута (238.7 м), высота пирамиды -484.4 фута (147.6 м). Длина ребра основания, деленная на высоту, приводит к соотношению Ф=1.618. [12]

После подробного изучение большого объема информации связанного с темой моего реферата можно сделать следующие выводы:

· Числовая последовательность Фибоначчи проявляется во многих разделах математики, биологии, искусства и т.д.

· Числа Фибоначчи являются универсальными, так как справедливы независимо от области применения.

· Золотое сечение является одним из ярких примеров использования ряда чисел Фибоначчи.

· Числа Фибоначчи и Золотое сечение требуют подробного изучения.

Ссылка действительна на 27.04.2012

Воробьев Н.Н. Числа Фибоначчи. Издание четвертое. Дополненное. – М. Наука, 1978

Вы что-нибудь слышали о Божественной гармонии или Золотом сечении? Задумывались ли о том, почему нам что-то кажется идеальным и красивым, а что-то отталкивает?

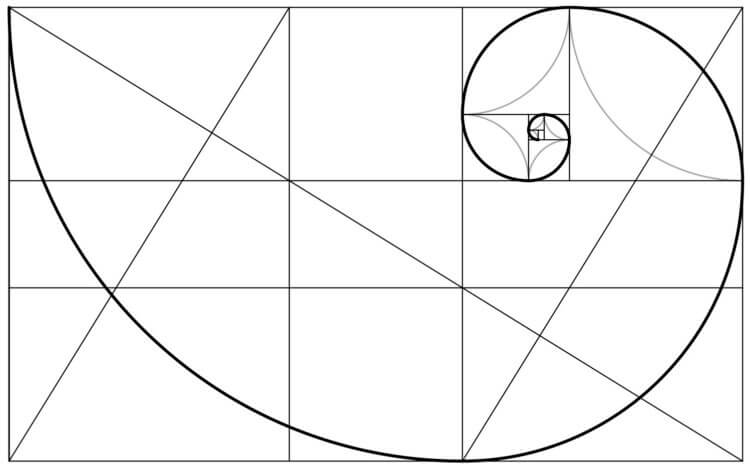
Если нет, то вы удачно попали на эту статью, потому что в ней мы обсудим золотое сечение, узнаем что это такое, как оно выглядит в природе и в человеке. Поговорим о его принципах, узнаем что такое ряд Фибоначчи и многое многое другое, включая понятие золотой прямоугольник и золотая спираль.

Да, в статье много изображений, формул, как-никак, золотое сечение — это еще и математика. Но все описано достаточно простым языком, наглядно. А еще, в конце статьи, вы узнаете, почему все так любят котиков =)

Что такое золотое сечение?

Если по-простому, то золотое сечение — это определенное правило пропорции, которое создает гармонию?. То есть, если мы не нарушаем правила этих пропорций, то у нас получается очень гармоничная композиция.

Наиболее емкое определение золотого сечения гласит, что меньшая часть относится к большей, как большая ко всему целому.

До наших современников золотое сечение дошло со времен Древней Греции, однако, бытует мнение, что сами греки уже подсмотрели золотое сечение у египтян. Потому что многие произведения искусства Древнего Египта четко построены по канонам этой пропорции.

Золотое сечение в математике

В чем же уникальность этой пропорции (а она, поверьте, есть)? Давайте для начала попробуем разобраться на примере отрезка. Итак, берем отрезок и делим его на неравные части таким образом, чтобы его меньшая часть относилась к большей, как большая ко всему целому. Понимаю, не очень пока ясно, что к чему, попробую проиллюстрировать наглядней на примере отрезков:

Итак, берем отрезок и делим его на два других, таким образом, чтобы меньший отрезок а, относился к большему отрезку b, так же, как и отрезок b относится к целому, то есть ко всей линии (a + b). Математически это выглядит так:

Этот правило работает бесконечно, вы можете делить отрезки сколь угодно долго. И, видите, как это просто. Главное один раз понять и все.

Кто такой Фибоначчи?

Последовательность Фибоначчи

Иными словами, последовательность Фибоначчи выглядит так:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987 и так далее.

Каждое число из ряда Фибоначчи, разделенное на последующее, имеет значение, стремящееся к уникальному показателю, которое составляет 1,618. Первые числа ряда Фибоначчи не дают настолько точное значение, однако по мере нарастания, соотношение постепенно выравнивается и становится все более точным.

Леонардо Пизанский — тот самый создатель числа Фибоначчи

Где используется число Фибоначчи

Проявление золотого сечения в природе

Эстетичность такой гармонизации мироздания воспринимается человеком, который всегда стремился улучшить окружающую его действительность, в качестве стабилизирующего природу закона. Находя золотое сечение в лице того или иного человека, мы инстинктивно воспринимаем собеседника в качестве гармоничной личности, чье развитие происходит без сбоев и нарушений. Этим можно объяснить то, почему иногда нам по непонятным причинам больше нравится одно лицо, чем другое. Оказывается, о наших возможных симпатиях позаботилась природа!

Как вы считаете, является ли повсеместное применение числа Фибоначчи в природе совпадением или свидетельством наличия некоего вселенского разума? Давайте попробуем обсудить этот вопрос в нашем Telegram-чате.

Наиболее распространенное определение золотого сечения гласит, что меньшая часть так относится к большей, как большая часть относится ко всему целому. Уникальное правило встречается во всех областях природы, науки и искусства, позволив некоторым именитым исследователям Средних Веков сделать предположение, что три основные части золотого сечения олицетворяют собой христианских Отца, Сына и Святого Духа.

Правилу золотого сечения следуют даже галактики. Наш Млечный Путь в этом плане не является исключением

Что такое золотое сечение

С точки зрения математики, золотое сечение представляет собой некую идеальную пропорцию, к которой каким-то образом стремится все живое и неживое в природе.

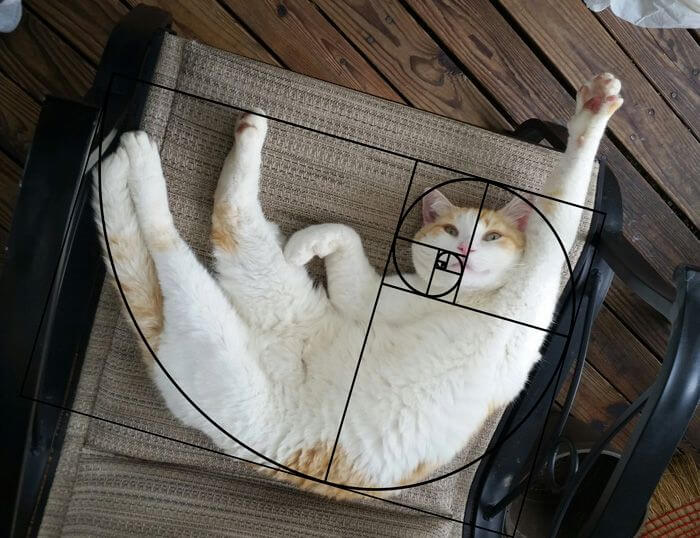
Даже коты неосознанно (хотя, кто знает?) следуют принципу золотого сечения, становясь любимцами большей части населения планеты

Есть ли в природе гармония? Несомненно, есть. А ее доказательством служит число Фибоначчи, происхождение которого нам еще только предстоит отыскать.

Свободное общение и обсуждение материалов

В Казахстане образовался 14-метровый вулкан, из жерла которого выплескивается вода. 🌋 Такие большие ледяные вулканы большая редкость, но самое явление возникает часто. Рассказываем, из-за чего они возникают и в каких местах. Они есть даже в космосе.

Знаете ли вы, что абсолютно все живые организмы нашей планеты имеют одного общего предка? Данное утверждение стало реальностью после изучения генетического к…

Зачастую мы ищем научное подтверждение ненаучных событий. Этим озадачивались многие ученые во все времена. Благо нынешние технологии подливают "масло в огонь…

Читайте также: