Какие приемы используют для доказательства тождеств кратко

Обновлено: 05.07.2024

Доказать тождество — это значит показать, что его обе части равны, т. е. его левая часть тождественно равна правой части для любых допустимых значений переменных.

1. преобразовать выражение в левой части и получить выражение в правой части;
2. преобразовать выражение в правой части и получить выражение в левой части;
3. преобразовать выражение в левой части, отдельно преобразовать выражение в правой части и получить одинаковые выражения;
4. преобразовать разность левой и правой частей и показать, что она равна нулю.

Преобразуем выражение в левой части:
a + b a + b 2 a − b − a − b a − b 2 a + b = a + b 2 − a − b 2 2 a − b a + b = a 2 + 2 ab + b 2 − a 2 − 2 ab + b 2 2 a − b a + b = = a 2 + 2 ab + b 2 − a 2 + 2 ab − b 2 2 a − b a + b = 4ab 2 a 2 − b 2 = 4 ⋅ a ⋅ b 2 ⋅ a 2 − b 2 = 2ab a 2 − b 2 .

b a − b − b 2 − ab a 2 − b 2 = b a + b a − b − b 2 − ab a − b a + b = b a + b a − b a + b − b 2 − ab a − b a + b = = b a + b − b 2 − ab a − b a + b = ab + b 2 − b 2 + ab a − b a + b = 2ab a 2 − b 2 .

В ходе изучения алгебры мы сталкивались с понятиями многочлен (например ($y-x$ ,$\ 2x^2-2x$ и тд) и алгебраическая дробь( например $\frac$ , $\frac$,$\ \frac$ и тд). Сходство этих понятий в том, что и в многочленах, и в алгебраических дробях присутствуют переменные и числовые значения, выполняются арифметические действия: сложение, вычитание, умножение, возведение в степень. Отличие этих понятий состоит в том, что в многочленах не производится деление на переменную, а в алгебраических дробях деление на переменную можно производить.

И многочлены, и алгебраические дроби в математике называются рациональными алгебраическими выражениями. Но многочлены являются целыми рациональными выражениями, а алгебраические дроби- дробно- рациональными выражениями.

Можно получить из дробно --рационального выражения целое алгебраическое выражение используя тождественное преобразование, которое в данном случае будет являться основным свойством дроби- сокращением дробей. Проверим это на практике:

Выполнить преобразование:$\ \frac$

Решение: Преобразовать данное дробно-рациональное уравнение можно путем использования основного свойства дроби- сокращения, т.е. деления числителя и знаменателя на одно и то же число или выражение, отличное от $0$.

Сразу данную дробь сократить нельзя,необходимо преобразовать числитель .

Преобразуем выражние стоящее в числителе дроби,для этого воспользуемся формулой квадрата разности:$a^2-2ab+b^2=^2$

Дробь имеет вид

Теперь мы видим, что в числителе и в знаменателе есть общий множитель --это выражение $x-2$, на которое произведем сокращение дроби

После сокращения мы получили, что исходное дробно-рациональное выражение $\frac$ стало многочленом $x-2$, т.е. целым рациональным.

Теперь обратим внимание на то, что тождественными можно считать выражения $\frac$ и $x-2\ $ не при всех значениях переменной, т.к. для того, чтобы дробно-рациональное выражение существовало и было возможно сокращение на многочлен $x-2$ знаменатель дроби не должен быть равен $0$ ( так же как и множитель, на который мы производим сокращение. В данном примере знаменатель и множитель совпадают, но так бывает не всегда).

Значения переменной, при которых алгебраическая дробь будет существовать называются допустимыми значениями переменной.

Поставим условие на знаменатель дроби: $x-2≠0$,тогда $x≠2$.

Значит выражения $\frac$ и $x-2$ тождественны при всех значениях переменной, кроме $2$.

Готовые работы на аналогичную тему

Тождественно равными выражениями называются те, которые равны при всех допустимых значениях переменной.

Тождественным преобразованием является любая замена исходного выражения на тождественно равное ему .К таким преобразованиям относятся выполнение действий: сложения, вычитания, умножение, вынесение общего множителя за скобку, приведение алгебраических дробей к общему знаменателю, сокращение алгебраических дробей, приведение подобных слагаемых и т.д. Необходимо учитывать ,что ряд преобразований , такие как, сокращение, приведение подобных слагаемых могут изменить допустимые значения переменной.

Приемы, использующиеся для доказательств тождеств

Привести левую часть тождества к правой или наоборот с использованием тождественных преобразований

Привести обе части к одному и тому же выражению с помощью тождественных преобразований

Перенести выражения , стоящие в одной части выражения в другую и доказать, что полученная разность равна $0$

Какое из приведенных приемов использовать для доказательства данного тождества зависит от исходного тождества.

Доказать тождество $^2- 2(ab+ac+bc)=a^2+b^2+c^2$

Решение: Для доказательства данного тождества мы используем первый из приведенных выше приемов, а именно будем преобразовывать левую часть тождества до ее равенства с правой.

Рассмотрим левую часть тождества:$\ ^2- 2(ab+ac+bc)$- она представляет собой разность двух многочленов. При этом первый многочлен является квадратом суммы трех слагаемых.Для возведения в квадрат суммы нескольких слагаемых используем формулу:

Далее для преобразования раскроем скобку $2(ab+ac+bc).$

Для этого нам необходимо выполнить умножение числа на многочлен.Вспомним, что для этого надо умножить общий множитель,стоящий за скобками на каждое слагаемое многочлена,стоящего в скобках.Тогда получим:

Теперь вернемся к исходному многочлену,он примет вид:

$^2- 2(ab+ac+bc)=\ a^2+b^2+c^2+2ab+2ac+2bc-(2ab+2ac+2bc)= a^2+b^2+c^2+2ab+2ac+2bc-2ab-2ac-2bc$

Приведем подобные слагаемые,тогда получим, что одночлены $2ab$, $2ac$,$\ 2bc$ и $-2ab$,$-2ac$, $-2bc$ взаимно уничтожатся, т.е. их сумма равна $0$.

$^2- 2(ab+ac+bc)=\ a^2+b^2+c^2+2ab+2ac+2bc-(2ab+2ac+2bc)= a^2+b^2+c^2+2ab+2ac+2bc-2ab-2ac-2bc=a^2+b^2+c^2$

Значит путем тождественных преобразований мы получили тождественное выражение в левой части исходного тождества

Заметим, что полученное выражение показывает, что исходное тождество --верно.

Обратим внимание, что в исходном тождестве допустимы все значения переменной, значит мы доказали тождество используя тождественные преобразования, и оно верно при всех допустимых значениях переменной.

Тождества в основном применяются для решения линейных уравнений.

Тождеством называется равенство, которое верно при всех значениях переменных.

Или другими словами, тождество — это равенство, которое выполняется на всём множестве значений переменных, входящих в него, например:

В этих выражениях при всех значениях a и b равенство верное.

2 выражения с равными значениями при всех значениях переменных являются тождественно равными.

Равенство x+2=5 может существовать не при всех значениях x, а лишь при x=3. Это равенство не будет тождеством, это будет уравнением. Кроме того, тождеством будет равенство, которое не содержит переменные, например 25 2 =625.

Примеры тождеств.

- Тождество Эйлера (кватернионы);

- Тождество Эйлера (теория чисел);

- Тождество четырёх квадратов;

- Тождество восьми квадратов;

Тождественные преобразования.

Тождественное преобразование выражения (преобразование выражения) – это подмена одних выражений другими, тождественно равными друг другу.

Для тождественных преобразований используют формулы сокращенного умножения, законы арифметики и другие тождества.

Выполним тождественные преобразования с такой дробью: .

Полученное тождество, при х ≠ 0 и х ≠ 1 (недопустимые значения), т.к. знаменатель левой части не может быть равен нулю.

Доказательство тождеств.

Для того, чтоб доказать тождество нужно сделать тождественные преобразования обеих или одной части равенства, и получить слева и справа одинаковые алгебраические выражения.

Например, доказать тождество:

Вынесем х за скобки:

Это равенство есть тождество, при х≠0 и х≠1.

Чтоб доказать, что равенство не является тождеством, нужно найти 1-но значение переменной (которое допустимо) у которой числовые выражения (которые были получены) станут не равными друг другу.

5−1 ≠ 5+1 — подставим, к примеру, 5.

Это равенство не тождество.

Разница между тождеством и уравнением.

Тождество верно при всех значениях переменных, а уравнение – это равенство, которое верно только при одном либо нескольких значениях переменной.

Логические законы объективны и не зависят от человеческого сознания. Это основа процесса мышления. Одним из главных можно назвать закон тождества, который находит применение не только в области логики, но и в других научных знаниях: математике, информатике, криминалистике, физике, химии и юриспруденции.

Основные законы логики

Логика — это раздел философии. Он представляет собой науку о формах и законах правильного мышления. Закон логики — необходимая связь между логическими формами в процессе построения последовательного рассуждения. Цель его состоит в формулировании правил и рекомендаций, с помощью которых можно найти путь к истине. Это не законы самого окружающего мира, а правила мышления о нём.

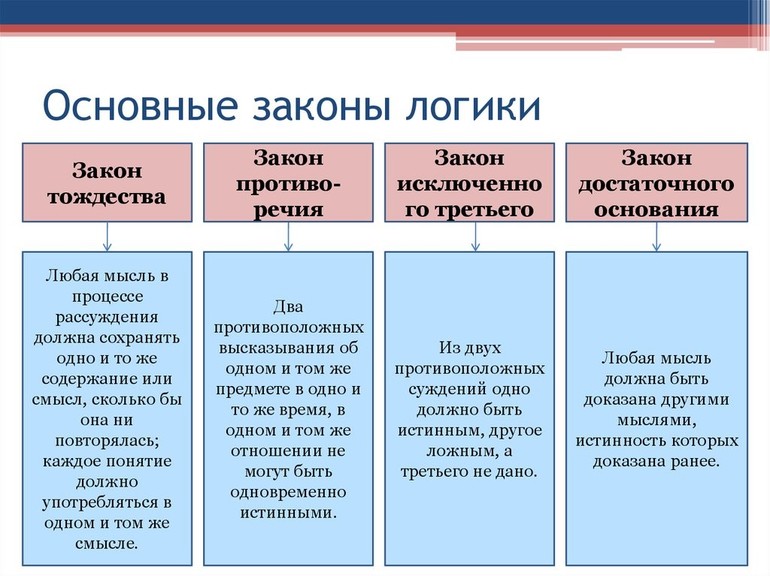
Аристотель, который создал классификацию свойств бытия, всесторонне определяющих субъект, впервые сформулировал три из четырёх логических законов и подразумевал под этим предпосылку для объективной связи мыслей в процессе размышления. Основными в формальной логике считаются законы:

• тождества;
• исключённого третьего;
• непротиворечия;
• достаточного основания.

Без этого закона невозможно установить, что такое логическое следование, и понять смысл доказательства.

Логический принцип тождественности

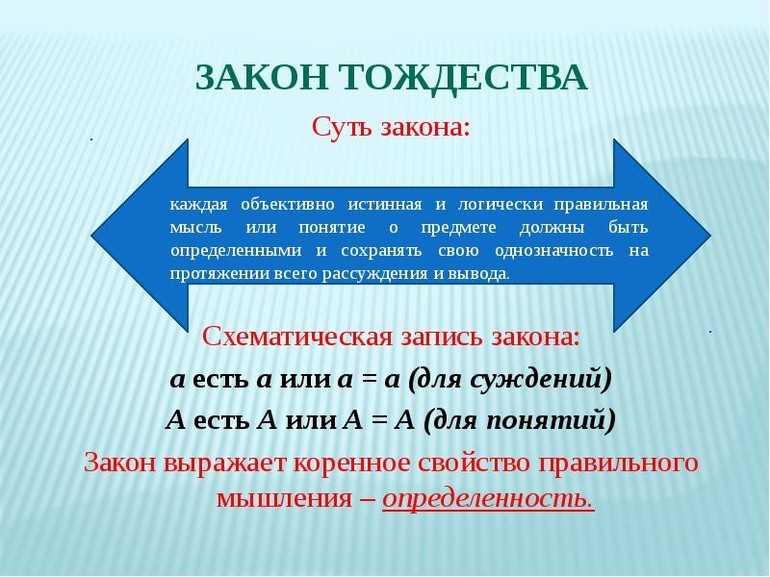
Тождество — это примерное равенство, сходство объектов по какому-либо показателю. Принцип (синоним слова закон) его — один из основных логических законов формальной логики как науки, в соответствии с которым в процессе размышления любое суждение должно оставаться тождественными самому себе.

• пусть установлено: по определённым признакам мысль А тождественна В. Тогда верно и утверждение, что В по тем же признакам тождественна А;
• если А по какому-то показателю равна В, а В при этом соответствует С, то А будет равна С.

1. Не сделал, то есть не совершил что-то плохое, за что можно наказать.
2. Не сделал что-то, что должен был выполнить.

Получилось, что в одно и то же понятие было вложено два различных смысла. Нарушение закона может выражаться в следующих формах:

1. Подмена или потеря предмета мысли.
2. Намеренное искажение.
3. Замена тезиса — нетождественность положения, которое пытаются доказать, исходному тезису.

Нарушение закона тождества ведёт к неясности мысли, что совершенно недопустимо во многих областях, например, в юриспруденции. Неточное определение или неправильно истолкованное понятие в сфере права способствует появлению беззакония и произвола, поэтому в процессе мышления принцип тождественности выступает в виде важного правила.

Этот закон вводит требование об отсутствии в ходе размышлений подмены или смешения мысли об объекте или замены предмета мысли. Нужно учитывать, что даже в законодательных актах часто попадаются двусмысленности, а это обязательно приводит к разночтениям в истолковании и неоднозначности в применении.

Виды преобразований

Тождеством в математике называется равенство, которое верно при всех значениях, входящих в него переменных для различных классов функций. Значение этого слова — полное сходство, подобие объектов, явлений друг другу или самим себе. К тождествам можно отнести:

1. Формулы сокращённого умножения в алгебре.
2. Тождество параллелограмма. Оно гласит, что сумма квадратов длин сторон параллелограмма равна сумме квадратов длин его диагоналей.
3. Основное тригонометрическое тождество sin 2 α + cos 2 α = 1, которое связывает квадраты функций синуса и косинуса для любых значений углов.
4. Тождество Эйлера (комплексный анализ).

Тождество Эйлера — e iπ + 1 = 0 — часто приводят как пример феноменального результата, который устанавливает неочевидную зависимость между геометрией (число пи) и математическим анализом (экспонента). Формула связывает пять фундаментальных математических констант:

• число e — основание натурального логарифма;
• i — мнимую единицу;
• число пи — соотношение длин окружности и диаметра;
• 1 и 0 — нейтральные элементы по операциям умножения и сложения соответственно.

Тождественным преобразованием называются операции, которые проводятся для замены исходного выражения на тождественно равное. Например, x 3 — xy 2 = x (x — y)(x + y) — это тождество, так как вынесение за скобки общего множителя и применение формул сокращённого умножения являются тождественными преобразованиями. Для демонстрации подставим вместо переменных x и y произвольные значения. Пусть x = 5; y = 4. Получим слева: 125 — 5 x 16 = 45, справа 5 (5 — 4)(5 + 4) = 45. Совпадение обеих частей равенства доказывает тождественность.

Способы доказательства

Равенство и тождество, которое относится к предельному случаю равенства, — это термины, используемые в математике при решении уравнений. Для доказательства тождества нужно сделать тождественные преобразования выражений в одной или обеих частях равенства и получить одинаковые результаты. При выполнении преобразований необходимо обращать внимание на область допустимых значений (ОДЗ) переменных. Эти операции могут суживать ОДЗ или оставлять её прежней.

При переходе от выражения x + (-y) к выражению (x — y) область допустимых значений переменных x и y будет прежняя. Переход от выражения (x — 5) к отношению (x — 5) 2 / (x — 5) приводит к сужению ОДЗ переменной x от (-ꚙ, +ꚙ) до (-ꚙ, 5) U (5, +ꚙ). Способы доказательства:

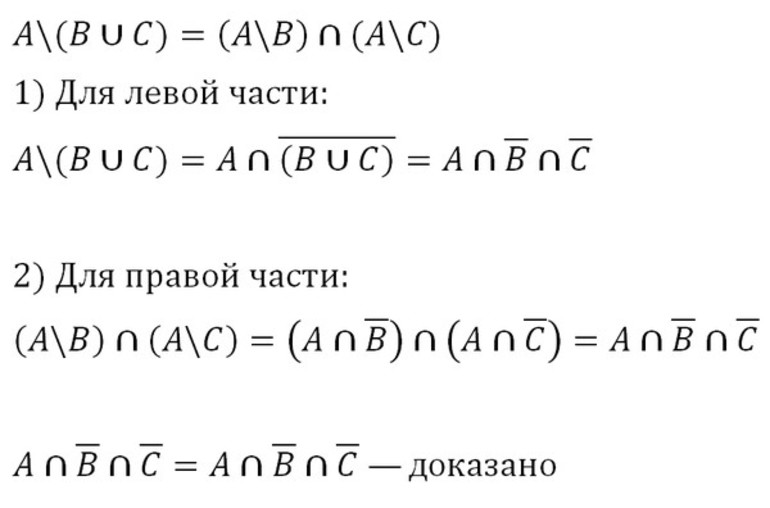
1. Применить тождественные преобразования к левой части. Если получится выражение, стоящее в правой части, то тождество считается доказанным.
2. Преобразовать таким же способом правую часть равенства. Если в результате получится выражение, стоящее в левой части, то доказательство получено.
3. Сделать тождественные преобразования левой и правой части равенства. Если будет достигнут одинаковый результат, то это служит доказательством тождественности обеих частей.
4. От правой части равенства отнять левую. Выполнить над разностью равносильные преобразования. Получение в итоге нуля считается доказательством тождественности частей.
5. Из левой части равенства вычесть правую и произвести над разностью тождественные преобразования. В итоге должен получиться нуль. Тождество будет верным.

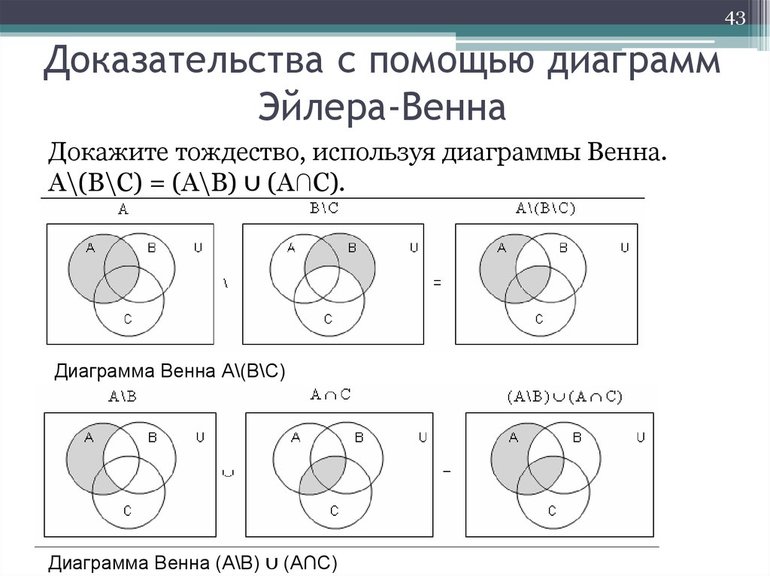
В теории множеств для доказательства тождественности часто используются круги или диаграммы Эйлера.

В них графическими методами наглядно можно представить различные операции над множествами: пересечение, объединение, разность, симметрическую разность. Существуют методы построения пересекающихся кругов Эйлера для любого выражения онлайн. Это тоже упрощает доказательство тождественности.

Чтобы доказать нетождественность двух частей выражения, требуется найти хотя бы одно значение переменной из области допустимых значений. При ее подстановке числовые выражения частей получатся неравными друг другу. Разница между уравнением и тождеством заключается в том, что первое может быть выполнено только при некоторых значениях переменных, которые будут его решением, а второе — при всех значениях.

Тождество — это многозначный термин, применяемый в философии, математике, физике. Понятие тождественности уникально по охвату им различной проблематики. С ним сталкиваются и школьники на уроках алгебры и геометрии, и крупные учёные при проведении многочисленных исследований в современной науке.

Читайте также:

  
• Как ты понимаешь изречение уважая человека уважаешь себя кратко
  
• Школа 2 златоуст педагогический состав
  
• Почему закон кулона является основным законом электростатики ответ кратко
  
• Что такое биоразнообразие кратко
  
• Школа апогей почему закрыли