Как появились логарифмы кратко
Обновлено: 05.07.2024
Цель:Узнать о широком применении логарифмов в сферах деятельности человека.
1. Найти и изучить историю о возникновении логарифмов.
2. Найти и рассмотреть ,где применяют логарифмы в жизни.
3. Найти интересные и удивительные факты о логарифмах.
4. Проанализировать полученную информацию и сделать выводы.
Основополагающий вопрос: Зачем нужны логарифмы"
Предметные вопросы:
•Кто создал логарифмы?
•Для чего они нужны?
•Где впервые применили логарифмы?
Объект исследования : Логарифм
Предмет исследования : Математика
Продукт: Презентация
Ход работы
1. Найти и изучить информацию о логарифмах.
2. Выяснить, где встречаются логарифмы в обычной жизни.
3. Сделать презентацию.
Источники информации
1. Интернет источники:
Основная часть
Глава 1 : История возникновения логарифма
Глава 2 : Создание собственного теста. Тестирование учащихся нашей школы.
Один из наиболее распространенных пауков, Эпейра, сплетая паутину, закручивает нити вокруг центра по логарифмическим спиралям.

Логарифмы возникли в 16 веке в связи с необходимостью проведения большого объема приближенных вычислений в ходе решения практических задач, и в первую очередь задач астрономии, (в частности, при определении положения судов по звездам и по Солнцу).
История возникновения логарифмов
Логарифмы с основанием ввел учитель математики Спейдел. Слово основание заимствовано из теории о степенях и перенесено в теорию логарифмов Эйлером. Глагол “логарифмировать” появился в 19 веке у Коппе. Коши первый предложил ввести различные знаки для десятичных и натуральных логарифмов. Обозначения, близкие к современным ввел немецкий математик Прингсхейм в 1893 году. Именно он обозначал логарифм натурального числа через ln. Определение логарифма как показателя степени данного основания можно найти у Валлиса (1665 год), Бернулли (1694 год).
Понятия функции тогда ещё не было, и Непер определил логарифм кинематически, сопоставив равномерное и логарифмически-замедленное движение; например, логарифм синуса он определил следующим образом
Логарифм данного синуса есть число, которое арифметически возрастало всегда с той же скоростью, с какой полный синус начал геометрически убывать.
К сожалению, все значения таблицы Непера содержали вычислительную ошибку после шестого знака. Однако это не помешало новой методике вычислений получить широчайшую популярность, и составлением логарифмических таблиц занялись многие европейские математики, включая Кеплера.
В 1620-е годы Эдмунд Уингейт и Уильям Отред изобрели первую логарифмическую линейку, до появления карманных калькуляторов — незаменимый инструмент инженера.

Эйлеру принадлежит и заслуга распространения логарифмической функции на комплексную область.
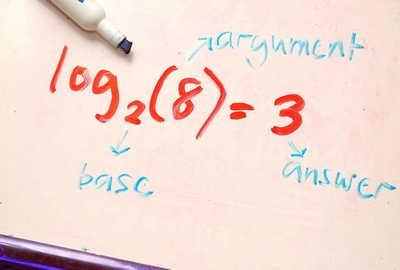
P. S. Старинные летописи рассказывают: А если у вас есть трудности с понимаем сущности логарифмов, как впрочем и других непростых понятий в высшей математике, то вам всегда поможет хороший репетитор по математике, которого можно найти в репетиторском центре “Гильдия наук” в городе Сочи. Данный центр оказывает образовательные услуги выпускникам школ при подготовке к ЕГЭ и ОГЭ и поможет вам получить высшие балы, как по математике, так и по другим дисциплинам.
Посвящаю памяти своей мамы Лидии Васильевны Семёновой, впервые познакомившей меня с логарифмами.
Долгожданный помощник астрономов
Логарифм тесно связан с более привычной всем функцией возведения в степень (1) и является одной из двух обратных функций к ней, наряду с операцией извлечения корня (2):

Если в формуле (1) переменной служит величина А, то мы имеем дело со степенной функцией. При переменном показателе степени х та же формула (1) определяет показательную функцию, которую иногда называют ещё антилогарифмом по основанию А. Логарифмирование (3) представляет собой поиск неизвестного показателя степени x из (1). Величина A называется основанием логарифма. Наиболее часто используют логарифмы по основанию 10, которые носят названия десятичных и обозначаются lg x, и логарифмы по основанию е = 2,71828… — натуральные логарифмы −ln x. Менее популярны, но имеют важное и самостоятельное значение двоичные логарифмы, которые с недавнего времени, согласно стандарту ISO 31-11, имеют пока ещё малоизвестное собственное обозначение lb x, но чаще записываются как log2x.
Например, если мы возводим число 10 в квадрат, в куб, в четвёртую степень, то соответственно имеем результатом 100, 1000 и 10000. Тогда логарифмами этих чисел по основанию 10 будут соответственно величины 2, 3 и 4 — показатели степени, в которые возводится число:

Поскольку мы используем десятичную систему счисления, логарифмы таких чисел совпадают с количеством нулей после единицы.

Графики трёх наиболее часто используемых логарифмических функций: двоичного, натурального и десятичного логарифмов.
Поясним это на простом примере умножения чисел 1265 и 432. Пусть в нашем распоряжении имеется таблица десятичных логарифмов. Тогда находим по ней lg 1265 и lg 432, подсчитываем их сумму. Получили логарифм ответа, который находим снова по таблице. В математической форме то, что мы проделали, выглядит так:
lg 1265·432 = lg 1265 + lg 432 ≈ 3,1020905+ + 2,6354837 = 5,7375742 ≈ lg 546480. Ответ: 1265·432 = 546480.
Точность ответа определяется числом знаков, с которым вычислены логарифмы в таблице.
На рубеже XVI—XVII веков такая замена была особенно долгожданной, поскольку развивающиеся науки требовали всё большего количества вычислений. По словам французского математика Пьера-Симона Лапласа (1749—1827), открытие логарифма как бы подарило учёным, в первую очередь астрономам, дополнительные годы жизни за счёт значительного сокращения громоздких расчётов.
Логарифмы Непера

Первооткрыватель
логарифмов
Джон Непер
(John Napier).
Как же Непер вычислял свои логарифмы? Со времён Архимеда было известно, что если составить последовательность целых чисел x в виде арифметической прогрессии и подставить эти числа в выражение (1), то полученные значения величины y будут располагаться в геометрической прогрессии — каждое следующее число будет больше предыдущего в A раз. Однако при попытке перейти в формуле (1) к дробным, а тем более к иррациональным величинам x возникали сложности, которые до Джона Непера никому так и не удалось решить. Фактически надо было перейти от последовательностей целых чисел к непрерывной функции с произвольным значением показателя степени x.
Гениальность подхода Джона Непера заключалась в том, что он для вычислений использовал так называемый кинематический метод. Непер задал равномерное движение точки x, которому соответствовало равнозамедленное движение точки у.

При вычислении логарифмов Джон Непер использовал кинематический метод. Он сопоставил движение двух точек по двум прямым: равномерное движение точки N на бесконечной прямой с началом в точке N0 и движение точки M на прямой конечной длины М0R. Скорость движения точки M равномерно уменьшалась пропорционально расстоянию, которое ей оставалось пройти до конечной точки R. При устремлении точки N в бесконечность точка M стремилась в точку R, не имея возможности её достигнуть. Если отметить на обеих прямых положения точек M и N, в которых они будут находиться через несколько равных промежутков времени, то на шкале логарифмов N получается арифметическая прогрессия, а на шкале аргументов M образуется прогрессия геометрическая из расстояний между соседними положениями этой замедленно движущейся точки. Такое соответствие точек на двух прямых как раз и представляло искомую логарифмическую зависимость между величинами.
По сути, Джон Непер предвосхитил дифференциальное исчисление в те времена, когда ещё не было самого понятия функции, функциональной связи между величинами. Для читателей, знающих высшую математику, скажем, что его зависимость между х и у выражается несложным дифференциальным уравнением:

Решение этого уравнения как раз и даёт логарифмическую зависимость в виде y = C − 10 7 ln x. Неопределённый коэффициент C у Непера из условия y(10 7 ) = 0 равен С = 10 7 ln(10 7 ) = 161180956,5.
Таким образом, полученная функция, которую Непер назвал логарифмом, заметно отличается от логарифмов современных, так как на самом деле имеет вид:



— фактическое основание логарифма непера, сам Непер основание логарифма не вводил.
Логарифмы Непера были рассчитаны для тригонометрических функций углов, находящихся в диапазоне 0—90 о с шагом в одну угловую минуту, с точностью до восьмого знака. Итогом расчётов стала первая в истории человечества таблица логарифмов. Она действительно позволяла заменить умножение многозначных чисел сложением, а их деление вычитанием, хотя это получалось немного более сложным образом, чем при использовании современных логарифмических функций.
Синусы, косинусы и тангенсы присутствовали в этих таблицах из-за того, что основной целью Непера являлось упрощение тригонометрических вычислений, с которыми связаны многие его работы. Надо отметить среди научных заслуг Джона Непера также вывод ряда формул из сферической тригонометрии, которые носят его имя.
Непер использовал оригинальные формулы для вычисления логарифмов и больше полагался на интуицию, чем на строгие доказательства. Из-за этого в его алгоритме была допущена ошибка, делавшая неверными цифры после шестого знака, что, впрочем, не помешало популярности метода. Таблицы Непера с подробным описанием их составления и использования до сих пор вызывают удивление и восхищение как пытливостью ума их автора, так и его терпением и настойчивостью.
Соавторы и продолжатели
Читайте также:

