Как определить внутренний угол зная дирекционные углы его сторон кратко

Обновлено: 02.07.2024

Внутренние углы треугольника с вершинами A , B , C находятся по формуле: Если сумма углов треугольника окажется меньше 180 0 , то при вычислении был найден не внутренний угол треугольника, а внешний, смежный с ним.
Известно, что если в треугольнике квадрат большей стороны больше суммы квадратов двух других сторон, то этот треугольник тупоугольный. Например, если AB 2 > BC 2 + AC 2 , то сторона AB лежит против тупого угла.

Правила ввода данных

Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus .
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).

Поиск

Строительные работы, а также перепланировка квартиры и подготовка к ее ремонту требуют не только строительных навыков, но и познаний в математике, геометрии и пр. Так, часто бывает нужно найти внутренний угол треугольника.

Как найти внутренний угол
Как найти углы правильного многоугольника
Как найти величину угла треугольника

Для нахождения внутреннего угла треугольника вспомните теорему о сумме углов треугольника.
Теорема: сумма углов треугольника равна 180°.
Из этой теоремы выделите пять следствий, которые могут помочь в расчете внутреннего угла.
1. Сумма острых углов прямоугольного треугольника равна 90°.
2. В равнобедренном прямоугольном треугольнике каждый острый угол равен 45°.
3. В равностороннем треугольнике каждый угол равен 60°.
4. В любом треугольнике либо все углы острые, либо два угла острые, а третий тупой или прямой.
5. Внешний угол треугольника равен сумме двух внутренних углов.

Пример 1:
Найти углы треугольника АВС, зная, что угол С на 15° больше, а угол И на 30° меньше угла А.
Решение:
Обозначьте градусную меру угла А через Х, тогда градусная мера угла С равна Х+15°, а угол В равен Х-30°. Так как сумма внутренних углов треугольника равна 180°, то вы получите уравнение:
Х+(Х+15)+(Х-30)=180
Решая его, вы найдете Х=65°. Таким образом угол А равен 65°, угол В равен 35°, угол С равен 80°.

Поработайте с биссектрисой угла. В треугольнике АВС угол А равен 60°, угол В равен 80°. Биссектриса АD этого треугольника отсекает от него треугольник АСD. Попробуйте найти углы этого треугольника. Постройте график для наглядности.
Угол DAB равен 30°, так как AD – биссектриса угла А, угол ADC равен 30°+80°=110° как внешний угол треугольника ABD (следствие 5), угол С равен 180°-(110°+30°)=40° по теореме о сумме углов треугольника ACD.

Еще для нахождения внутреннего угла вы можете использовать равенство треугольников:
Теорема 1: Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

На основе Теоремы 1 устанавливается Теорема 2.
Теорема 2: Сумма любых двух внутренних углов треугольника меньше 180°.
Из предыдущей теоремы вытекает Теорема 3.

Теорема 3: Внешний угол треугольника больше любого внутреннего угла, не смежного с ним.
Также для вычисления внутреннего угла треугольника можно использовать теорему косинусов, но только в том случае, если известны все три стороны.

Вспомните теорему косинусов: Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:
a2=b2+c2-2bc cos A
или
b2=a2+c2- 2ac cos B
или
с2=a2+b2-2ab cos C

Прямой геодезической задачей называется способ определения координат какой-либо точки по известным координатам другой точки, дирекционному углу и расстоянию между ними.

Пусть точка A (рисунок 30) имеет координаты х₁ и у₁. Из точки А на точку В определен дирекционный угол α_1,2 и между точками измерено расстояние S.

Необходимо найти координаты х₂ и у₂ точки В.

Решение. Проведем через точки А и В линии, параллельные осям координат. Из образовавшихся построений искомые координаты точки выразятся:

Следовательно, решение прямой задачи сводится к отысканию значений отрезков АС и СВ.

Отрезки АС и СВ являются катетами прямоугольного треугольника ABC и равны проекциям линии АВ на оси координат.

Проекции горизонтальных проложений линии S на оси X и Y называются приращениями координат и обозначаются соответственно AС = Δх и ВС=Δу.

Приращения координат Δх и Δу могут быть положительными и отрицательными. Знак приращения определяется значением дирекционного угла линии АВ.

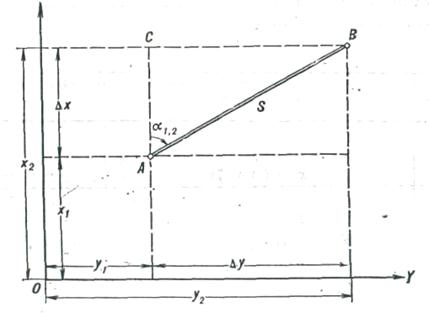
Рисунок 30 – Прямая (обратная) геодезическая задача

Пример. Приращения координат точки В относительно точки А будут положительными (I четверть). Приращения координат точки A относительно точки В будут отрицательными (III четверть).

Значения приращений координат находят из соотношений прямоугольного треугольника ABC:

Δх = S·cos α_{1, 2}; Δу = S·sin α_{1, 2} (8)

отсюда значения координат точки Вбудут:

Практическое решение прямой геодезической задачи производится на вычислительных машинах с использованием таблиц натуральных значений тригонометрических функций.

Вычисления выполняют в следующим порядке (таблица 6).

Таблица 6 – Порядок решения прямой геодезической задачи

№ действия	Элементы формул	Величина
α_{1, 2} х₂ = (1) + (7)	200 о 48'00" 6 о 106 о 845,1

Продолжение таблицы – 6

№ действия	Элементы формул	Величина
х₁ Δх = (3)·(6) Cos α_{1, 2} S Sin α_{1, 2} Δу = (3) · (5) y₁ y₂ = (2) + (8) s_конр =	6 о 115 105,3 - 8 260,2 - 0,934 826 8 836,1 - 0,55 107 - 3 137,8 7 534 664,7 7 531 526,9 8 836,1

- выписывают значения исходных данных х₁, y₁, S и α_{1, 2} (действия 1 ‑ 4);

- вычисляют приращения координат Δх и Δу (действия 5 – 8);

- вычисляют координаты х₂, y₂ точки В (действия 9 и. 10);

- проводят контроль вычислений путем определения значения s_конр по формуле

Расхождение S и S_конр более чем на единицу последнего знака свидетельствует о наличии ошибок, которые выявляют повторной проверкой всех вычислений.

Обратной геодезической задачей называется способ определения дирекционного угла и расстояния между двумя точками по известным их координатам.

Возвратимся к рисунку 30. Из условия обратной задачи известны: прямоугольные координаты точек А и В (х₁ и y₁; х₂ и y₂).

Необходимо найти расстояние s между точками А и В и дирекционный угол α_{1, 2} из точки А на точку В.

Решение. Искомые величины находят из соотношений прямоугольного треугольника ABC:

По значению тангенса с помощью тригонометрических таблиц определяют величину только острого угла. Острый угол, отсчитываемый от ближайшего направления оси абсцисс (северного или южного) до направления данной линии, называется румбом и обозначается буквой r.

Для отыскания значения дирекционного угла по значению румба определяют четверть, в которой находится искомое направление.

Четверть, в которой находится направление АВ, определяют по знакам приращений координат Δх и Δу, вычисляемых как разности абсцисс и ординат:

Формулы перехода от румба к дирекционному углу в зависимости от знака приращения координат приведены в таблице 7.

Таблица 7 – Переход от румба к дирекционному углу

Четверть круга	Знак приращения	Формулы перехода от румба к дирекционному углу
Δх	Δу
I II III IV	+ – – +	+ + – –	α = r α = 180 o – r α = 180 o + r α = 360 o – r

Искомое расстояние S определяют по формулам (10).

Наличие двух вариантов формул обеспечивает надежный контроль вычисления расстояния.

Вычисление расстояний и дирекционных углов при решении обратной геодезической задачи производят с использованием вычислительных машин и таблиц натуральных значений тригонометрических функций в следующем порядке, таблица 8:

Таблица 8 – Решение обратной геодезической задачи.

№ действия	Элементы формул	Величина
y₂ у₁. Δу = (4) – (2) x₂ x₁ Δх = (3) – (1) tg α_{1, 2} = (6) : (5) r	7 579 739,3 7 580 202,1 - 462,8 6 406 199,0 6 411 279,2 - 5 080,2 0,091 099 5о 12'19"

Продолжение таблицы 8

№ действия	Элементы формул	Величина
α_{1, 2} Sin α_{1, 2} Cos α_{1, 2} S₁ S₂ S_ср	185 о 12'19" 0,090 724 0,995 786 5 101,2 5 101,2 50 101,2

- выписывают координаты исходных пунктов. х₁, y₁, х₂, у₂ (действия 1 ‑ 4);

- вычисляют приращения координат Δх и Δу (действия 5 и 6); при этом всегда из координат второй точки алгебраически вычитают координаты первой точки;

- вычисляют тангенс дирекционного угла (действие 7);

- по тангенсу угла находят румб, который затем переводят в дирекционный угол с помощью таблицы 7, выбирают из таблиц синус и косинус этого угла (действия 8 – 11);

- дважды вычисляют расстояние s и за окончательное значение берут среднее из обоих результатов, при этом расхождение S₁ – S₂ не должно превышать более двух единиц последнего знака (действия 12 – 14).

Решением треугольника называется определение всех его сторон и углов по трем известным элементам, из которых хотя бы один должен быть его стороной.

Решение треугольника осуществляют по формулам соотношений его элементов, известных из курса тригонометрии.

Обозначив в треугольнике AВС (рисунок 31) стороны через а, в и с, а углы через А, В и С, запишем основные соотношения:

А + В + С = 180° (теорема суммы углов);

а 2 = в 2 + с 2 – 2·в·сcos A (теорема косинусов);

и дополнительные соотношения:

Sin A = Sin· (B + C);

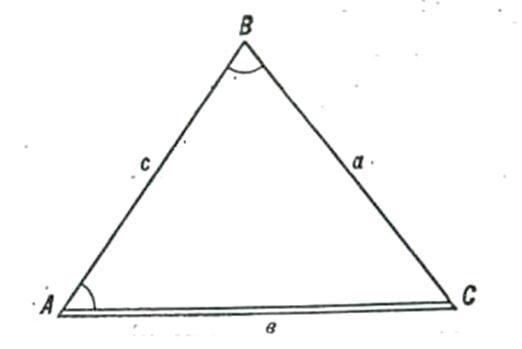
Рисунок 31 – Треугольник

Пример. Пусть в треугольнике ABC (рисунок 31) известны сторона в и углы А и В. Необходимо найти угол С и стороны а и с.

Решение проводят в следующем порядке:

- угол С находят по теореме суммы углов

- стороны а и с вычисляют по теореме синусов

- контроль вычислений осуществляют по формуле

Пример вычислений приведен в таблице 9.

Таблица 9 – Решение треугольника

№ действия	Элемент формулы	Величина
А	86 о 15'43"
В С = [180 o – (1) + (2)] Контроль: (1) + (2) +(4) = 180 о	46 о 34'52" 47 о 09'25" 180 о 00'00"
Sin A Sin B Sin C	0,997 873 0,726 348 0,733 220
а = (3) в с = (3) Контроль: а_контр = (10)	6 о 448,3 4 о 693,7 4 о 738,1 6 о 448,3

Контрольные вопросы и упражнения:

1. Дать определение прямой и обратной геодезических задач.

2. Дать вывод формул решений прямой (обратной) геодезической задачи.

3. Решить прямую задачу по данным: x₁ =6 104 172,8; y₁ = 5 565 542,8;

s = 4 021,4; α_{1, 2} =57°57'54".

Ответ: x₂ = 6 106 212,4; у₂ = 5 568 802,5.

4. Решить обратную задачу по данным:

x₁ = 6 114 133,5; х₂ = 6 107 134,0; у₁ = 5.565 596,8; у₂ = 5 574 985,3.

Ответ: α_{1, 2} = 126°42'21"; s =11710,5.

5. Решить треугольник по данным:

а) A = 86°49'11"; В = 36°52'12"; в = 7 211,2.	Ответ: С = 56°18'37"; а = 12 000,1; с = 10 000,1.
б) а=5590,2; s = 9 340,7; С = 84°46'51".	Ответ: с = 10 440,2; А = 32°13'26"; В = 62°59'43".
в) а = 10 440,2; в = 12530,0; с = 8 944,2.	Ответ: А = 55°10'30"; В = 80°08'05"; С = 44°41 '25".

Обратная геодезическая задача

Прямая геодезическая задача

Необходимо найти координаты х₂ и у₂ точки В.

Следовательно, решение прямой задачи сводится к отысканию значений отрезков АС и СВ.

Рисунок 30 – Прямая (обратная) геодезическая задача

Значения приращений координат находят из соотношений прямоугольного треугольника ABC:

Δх = S·cos α_{1, 2}; Δу = S·sin α_{1, 2} (8)

отсюда значения координат точки Вбудут:

Вычисления выполняют в следующим порядке (таблица 6).

Таблица 6 – Порядок решения прямой геодезической задачи

№ действия	Элементы формул	Величина
α_{1, 2} х₂ = (1) + (7)	200 о 48'00" 6 о 106 о 845,1

Продолжение таблицы – 6

№ действия	Элементы формул	Величина
х₁ Δх = (3)·(6) Cos α_{1, 2} S Sin α_{1, 2} Δу = (3) · (5) y₁ y₂ = (2) + (8) s_конр =	6 о 115 105,3 - 8 260,2 - 0,934 826 8 836,1 - 0,55 107 - 3 137,8 7 534 664,7 7 531 526,9 8 836,1

- выписывают значения исходных данных х₁, y₁, S и α_{1, 2} (действия 1 ‑ 4);

- вычисляют приращения координат Δх и Δу (действия 5 – 8);

- вычисляют координаты х₂, y₂ точки В (действия 9 и. 10);

- проводят контроль вычислений путем определения значения s_конр по формуле

Необходимо найти расстояние s между точками А и В и дирекционный угол α_{1, 2} из точки А на точку В.

Решение. Искомые величины находят из соотношений прямоугольного треугольника ABC:

Таблица 7 – Переход от румба к дирекционному углу

Четверть круга	Знак приращения	Формулы перехода от румба к дирекционному углу
Δх	Δу
I II III IV	+ – – +	+ + – –	α = r α = 180 o – r α = 180 o + r α = 360 o – r

Искомое расстояние S определяют по формулам (10).

Наличие двух вариантов формул обеспечивает надежный контроль вычисления расстояния.

Таблица 8 – Решение обратной геодезической задачи.

№ действия	Элементы формул	Величина
y₂ у₁. Δу = (4) – (2) x₂ x₁ Δх = (3) – (1) tg α_{1, 2} = (6) : (5) r	7 579 739,3 7 580 202,1 - 462,8 6 406 199,0 6 411 279,2 - 5 080,2 0,091 099 5о 12'19"

Продолжение таблицы 8

№ действия	Элементы формул	Величина
α_{1, 2} Sin α_{1, 2} Cos α_{1, 2} S₁ S₂ S_ср	185 о 12'19" 0,090 724 0,995 786 5 101,2 5 101,2 50 101,2

- выписывают координаты исходных пунктов. х₁, y₁, х₂, у₂ (действия 1 ‑ 4);

- вычисляют тангенс дирекционного угла (действие 7);

Решение треугольника осуществляют по формулам соотношений его элементов, известных из курса тригонометрии.

А + В + С = 180° (теорема суммы углов);

а 2 = в 2 + с 2 – 2·в·сcos A (теорема косинусов);

и дополнительные соотношения:

Sin A = Sin· (B + C);

Рисунок 31 – Треугольник

Решение проводят в следующем порядке:

- угол С находят по теореме суммы углов

- стороны а и с вычисляют по теореме синусов

- контроль вычислений осуществляют по формуле

Пример вычислений приведен в таблице 9.

Таблица 9 – Решение треугольника

№ действия	Элемент формулы	Величина
А	86 о 15'43"
В С = [180 o – (1) + (2)] Контроль: (1) + (2) +(4) = 180 о	46 о 34'52" 47 о 09'25" 180 о 00'00"
Sin A Sin B Sin C	0,997 873 0,726 348 0,733 220
а = (3) в с = (3) Контроль: а_контр = (10)	6 о 448,3 4 о 693,7 4 о 738,1 6 о 448,3

Контрольные вопросы и упражнения:

1. Дать определение прямой и обратной геодезических задач.

2. Дать вывод формул решений прямой (обратной) геодезической задачи.

3. Решить прямую задачу по данным: x₁ =6 104 172,8; y₁ = 5 565 542,8;

1. Проверка полевых вычислений и определение поправок в измерения длин линий

_______ Камеральные работы при теодолитной съемке заключаются в вычислении координат точек теодолитного хода и в построении плана .

_______ Далее вычисляются средние значения длин линии:

_______ В каждую длину линии вводятся поправки по формуле:

_______ Поправки вводятся при:

_______ После уравнивания углов производится вычисление дирекционных углов всех сторон теодолитного хода. _______ Вычисленные дирекционные углы переводятся в румбы.

2. Связь между дирекционными углами и горизонтальными углами теодолитного хода

_______ Дирекционный угол линии последующей равен дирекционному углу линии предыдущей плюс 180 0 минус угол вправо по ходу лежащий.

3. Обработка угловых измерений замкнутого теодолитного хода

_______ где f_β – угловая невязка.

_______ где n –вершина углов, следовательно:

_______ Если полученная невязка является допустимой , она распределяется поровну на все углы. Поправки в углы вводятся со знаком, противоположным знаку невязки. Сумма исправленных углов должна быть в точности равна теоретической сумме.

4. Угловая невязка разомкнутого теодолитного хода

Для вычисления ∑β _теор. найдем дирекционные углы всех сторон хода:

_______ где α_нач. и α_кон. – дирекционные углы сторон опорной сети, тогда:

_______ Подсчет допустимой невязки и ее распределение производится так же, как и для замкнутого хода .

5. Невязки в диагональном ходе

_______ Диагональный ход является разомкнутым ходом , поэтому его обработка производится так же, как и у разомкнутого хода. Например, для следующего рисунка.

_______ После обработки угловых измерений вычисляются дирекционные углы и румбы всех сторон хода.

_______ Причем вычисление дирекционных углов производится обязательно с контролем .

6. Прямая и обратная геодезические задачи

6.1. Прямая геодезическая задача: по координатам отрезка прямой (начала), его длине и направлению определить координаты конца отрезка

_______ Прямая геодезическая задача применяется при вычислении координатных точек теодолитного хода.

6.2. Обратная геодезическая задача: по координатам начала и конца отрезка прямой найти его длину и направление

_______ Далее вычисляют arctg и находят числовое значение румба. Название румба определяют по знакам приращений координат, от румба переходят к дирекционному углу.
Длина линии может быть найдена по следующим формулам:

_______ Обратная геодезическая задача применяется при подготовке данных для перенесения проектов сооружений в натуру.

7. Уравнивание приращений координат

_______ Уравниванием называется совокупность математических операций, выполняемых для получения вероятнейшего значения геодезических координат точек земной поверхности и для оценки точности результатов измерений.

_______ Уравнивание проводится для устранения невязок, обусловленных наличием ошибок в избыточно измеренных величинах, и для определения вероятнейших значений искомых неизвестных или их значений, близких к вероятнейшим. В процессе уравнвиания это достигается путём определения поправок к измеренным величинам (углам, направлениям, длинам линий или превышениям).

7.1. Вычисление координат точек теодолитного хода

_______ Из решения прямой геодезической задачи по известным длинам сторон и румбам вычисляются приращения координат для каждой стороны хода по формулам:

_______ Далее вычисляются невязки в приращениях координат замкнутого хода.

7.2. Вычисление невязок в приращениях координат замкнутого хода

_______ Из геометрии известно, что сумма проекций сторон многоугольника на любую ось равна нулю, следовательно:

_______ Под влиянием ошибок измерений замкнутый полигон будет разомкнутым на величину f_р – абсолютная невязка в периметре полигона.

_______ Если полученная невязка недопустима, то необходимо произвести повторное измерение длин линий.

_______ Если невязки допустимы, то они распределяются на приращения координат пропорционально длинам сторон с противоположным знаком, то есть сумма исправленных приращений должна быть точно равна теоретической сумме – в данном случае равна нулю.

7.3. Вычисление невязок в приращениях координат разомкнутого теодолитного хода

_______ Определение допустимости невязок и их распределения производится так же, как для замкнутого теодолитного хода.

Для диагонального хода, например:

_______ По исправленным значениям приращений координат вычисляются координаты всех точек хода по формулам:

8. Построение плана

_______ Построение плана выполняются в следующей последовательности :
1) построение координатной сетки,
2) нанесение вершин теодолитного хода по координатам,
3) нанесение на план контуров местности,
4) оформление плана.

8.1. Построение координатной сетки

_______ Координатная сетка строится обычно со стороной 10х10 см .
Используется два способа :

_______ 1) построение сетки с помощью линейки Дробышева:

_______ Построение сетки основано на построении прямоугольного треугольника с катетами 50x50 см и гипотенузой 70,711 см ;

2) построение сетки с помощью циркуля, измерителя и масштабной линейки:

_______ Этот способ применяется при размере плана меньше, чем 50 см . Сетка контролируется путем сравнения длин сторон или диагоналей квадратов. Допустимое отклонение – 0,2 мм . Построенную сетку подписывают координатами так, чтобы участок поместился.

_______ Вершины теодолитного хода наносятся на план по координатам относительно сетки с помощью измерителя и поперечного масштаба.

_______ Контроль правильности построения точек выполняется по известным расстояниям между точками. Допустимое расхождение – 0,3 мм в масштабе плана.

_______ Например: 1:2000 – 0,6 м .

_______ Контуры местности наносятся на план в соответствии с абрисами.

_______ Оформление плана выполняется в строгом соответствии с условными знаками, установленными для данного масштаба.

Дирекционный угол (α) – это угол между проходящими через данную точку направлением на ориентир и линией параллельной оси абсцисс, отчитываемой от северного направления оси абсцисс по ходу часовой стрелки оси 0 до 360°.

Рисунок 1. — Дирекционный угол.

Дирекционные углы направлений измеряются преимущественно по карте или определяются по магнитным азимутам.

Дирекционный угол ориентирного направления может определяться геодезическим или гироскопическим способом, из астрономических наблюдений, с помощью магнитной стрелки буссоли и по контурным точкам карты (аэрофотоснимка).

При геодезическом способе ориентирования дирекционный угол ориентирного направления может быть получен непосредственно из каталога (списка) координат, решением обратной геодезической задачи по координатам геодезических пунктов, при выполнении засечек или прокладке полигонометрического хода одновременно с определением координат привязываемых точек, а также путем передачи угловым ходом от направления с известным дирекционным углом.

При гироскопическом способе ориентирования с помощью гирокомпаса определяют истинный (астрономический) азимут ориентирного направления, а затем переходят к дирекционному углу этого направления. Азимут ориентирного направления с помощью гирокомпаса определяется по двум, трем (четырем) точкам реверсии. Увеличение числа точек реверсии до трех (четырех) обеспечивает контроль и повышает точность определения дирекционного угла.

При астрономическом способе ориентирования дирекционный угол ориентирного направления определяют путем перехода от азимута светила к азимуту ориентирного направления, а от последнего — к дирекционному углу. Азимут светила вычисляют по результатам наблюдений, выполненных на местности с данной точки. Азимут ориентирного направления из астрономических наблюдений может быть получен и с помощью азимутальной насадки АНБ-1 к буссоли ПАБ-2А непосредственно на местности без выполнения вычислений.

Способ определения дирекционного угла ориентирного направления из астрономических наблюдений является наиболее точным.

Работы в поле при этом способе заключаются в измерении горизонтального угла Q между направлением на светило и заданным направлением в момент времени наведения прибора на светило. По моменту времени наблюдения светила вычисляют азимут а светила, от него переходят к астрономическому азимуту А направления на ориентир: A’ = a + Q. Зная значение сближения меридианов у в точке наблюдения, определяют дирекционный угол с ориентирного направления: a = A — y.

При определении дирекционного угла ориентирного направления с помощью магнитной стрелки буссоли на местности сначала получают магнитный азимут ориентирного направления, а затем, учитывая поправку буссоли, переходят к дирекционному углу. Дирекционный угол ориентирного направления определяется по формуле: а = Ат + (±dАт).

По карте (аэрофотоснимку) дирекционный угол ориентирного направления получают решением обратной геодезической задачи по координатам двух контурных точек Координаты контурных точек при этом определяются по карте (аэрофотоснимку) с помощью циркуля измерителя и поперечного масштаба. Точность полученного дирекционного угла будет тем выше, чем больше расстояние между начальной и ориентирной точками и чем точнее определены координаты этих точек.

Дирекционный угол по карте также можно определить с помощью хордоугломера. Для этого опознают на карте исходную и ориентирную точки, проводят через них прямую линию и получают на карте ориентирное направление. Измерив с помощью хордоугломера угол между северным направлением вертикальной линии километровой сетки карты и ориентирным направлением, получают дирекционный угол этого направления.

Свойства дирекционных углов: дирекционные углы α₁=α₂=α₃ так как параллельные линии пересекаются одной линией. Следовательно, углы равны.

Рисунок 2. — Дирекционные углы.

Дирекционные углы могут быть прямыми и обратными (они отличаются на 180°):

Рисунок 3. — Прямые и обратные дирекционные углы.

В зависимости от выбора системы поверхностных координат или проекции земного эллипсоида на плоскость дирекционный угол может иметь собственное название. Например, геодезическийдирекционный угол, гауссов дирекционный угол и т.д.

Читайте также: