Что значит разложить вектор по двум данным векторам 9 класс кратко
Обновлено: 28.06.2024
В данной публикации мы рассмотрим, каким образом можно разложить вектор по двум базисным векторам, а также разберем пример решения задачи по этой теме.
Принцип разложения вектора
Для того, чтобы разложить вектор b по базисным векторам , требуется определить такие коэффициенты , при которых линейная комбинация векторов равняется вектору b , то есть:
Пример задачи
Разложим вектор по двум базисным векторам и .
Решение:
1. Векторное уравнение выглядит так:
3. Теперь нужно решить систему. Из второго уравнения получаем:
.
Подставляем полученное выражение в первое уравнение:
2 · (1 + 3y) + y = 16
2 + 6y + y = 16
7y = 14
y = 2
Урок 4: Координаты вектора. Разложение вектора по двум неколлинеарным векторам
Координаты вектора. Разложение вектора по двум неколлинеарным векторам.
Если векторы a ⃗ и b ⃗ коллинеарны и a ⃗ ≠ 0 ⃗ , то существует такое число k, что b ⃗ = k a ⃗ .
Пусть a ⃗ и b ⃗ – два данных вектора. Если вектор p представлен в виде p ⃗ = x a ⃗ + y b ⃗ , где x и y – некоторые числа, то говорят, что вектор p ⃗ разложен по векторам a ⃗ и b ⃗ . Числа x и y называются коэффициентами разложения.
Теорема
На плоскости любой вектор можно разложить по двум данным неколлинеарным векторам, причем коэффициенты разложения определяются единственным образом.
Напомню, что для задания прямоугольной системы координат нужно провести две взаимно перпендикулярные прямые, на каждой из них выбрать направление (оно обозначается стрелкой) и выбрать единицу измерения отрезков. При выбранной единице измерения отрезков длина каждого отрезка выражается положительным числом.
В дальнейшем под длиной отрезка мы будем понимать это число.
i ⃗ и j ⃗ так, чтобы направление вектора i ⃗ совпало с напралением оси Ox, а направление вектора j ⃗ – с направлением оси Oy. Векторы i ⃗ и j ⃗ назовем координатными векторами.
Координатные векторы не коллинеарны, поэтому любой вектор p ⃗ можно разложить по координатным векторам, т.е. представить в виде p ⃗ = x i ⃗ + y j ⃗ , причем коэффициенты разложения (числа x и y) определяются единственным образом. Коэффициенты разложения вектора p ⃗ по координатным векторамназываются координатными векторами p ⃗ в данной системе координат. Координаты вектора будем записывать в фигурных скобках после обозначения вектора: p ⃗ < x ; y >.
Так как нулевой вектор можно представить в виде 0 ⃗ = 0 . i ⃗ + 0 . j ⃗ , то его координаты равны нулю: 0 ⃗ < 0 ; 0 >. Если векторы a ⃗ = x 1 i ⃗ + y 1 j ⃗ и b ⃗ = x 2 i ⃗ + y 2 j ⃗ равны, то x1 = x2 и y1 = y3. Таким образом, координаты равных векторов соответственно равны.
Рассмотрим правила, позволяющие по координатам векторов находить координаты их суммы, разности и произведения вектора на число.
Каждая координата суммы двух или более векторов равна сумме соответствующих координат этих векторов.
Докажем это утверждение для двух векторов. Рассмотрим векторы a < x 1 ; y 1 >и b < x 2 ; y 2 >. Так как a ⃗ = x 1 i ⃗ + y 1 j ⃗ и b ⃗ = x 2 i ⃗ + y 2 j ⃗ ,то, пользуясь свойствами сложения векторов и умножения вектора на число, получим:
a ⃗ + b ⃗ = x 1 i ⃗ + y 1 j ⃗ + x 2 i ⃗ + y 2 j ⃗ = ( x 1 + x 2 ) i ⃗ + ( y 1 + y 2 ) j ⃗ .
Следовательно, что координаты вектора a ⃗ + b ⃗ равны < x 1 + x 2 ; y 1 + y 2 >.
Аналогично доказывается следующее утверждение:
Каждая координата разности двух или более векторов равна разности соответствующих координат этих векторов.
Иными словами, если a ⃗ < x 1 ; y 1 > и b ⃗ < x 2 ; y 2 > – данные векторы, то вектор a ⃗ – b ⃗ имеет координаты < x 1 - x 2 ; y 1 - y 2 >.
Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число.
В самом деле, пусть вектор a ⃗ имеет координаты < x ; y >. Найдем координаты вектора k a ⃗ , где k – произвольное число. Так как a ⃗ = x i ⃗ + y j ⃗ , то kx i ⃗ + ky j ⃗ . Отсюда следует, что координаты вектора k a ⃗ равны < kx ; ky >.
Рассмотренные правила позволяют определить координаты любого вектора, представленного в виде алгебраической суммы данных векторов с известными координатами.
Найти координаты вектора a ⃗ + b ⃗ , если a ⃗ < 3 ; 2 >, b ⃗
Чтобы найти координаты вектора суммы, надо сложить соответствующие координаты данных векторов, получим:
a ⃗ + b ⃗ имеет координаты , то есть
Найти координаты вектора 2 a ⃗ , если a ⃗
Значит, вектор 2 a ⃗ имеет координаты , то есть
Итак, сегодня мы узнали, что любой вектор можно разложить по двум неколлинеарным векторам, ввели понятие координат вектора и рассмотрели правила, позволяющие находить координаты суммы, разности векторов, и произведения вектора на число. А в следующий раз мы найдем связь между координатами вектора и координатами его начала и конца.
Докажем сначала лемму 1 о коллинеарных векторах.

Возможны два случая: Рассмотрим эти случаи в отдельности.
1) Возьмём число Так как k ≥ 0, то векторы сонаправлены (рис. 273, а). Кроме того, их длины равны: Поэтому .
2) Возьмём число Так как k Лемма доказана.

Пусть и — два данных вектора. Если вектор представлен в виде где х и у — некоторые числа, то говорят, что вектор разложен по векторам и . Числа х и у называются коэффициентами разложения. Докажем теорему о разложении вектора по двум неколлинеарным векторам.
Пусть и — данные неколлинеарные векторы. Докажем сначала, что любой вектор можно разложить по векторам и Возможны два случая.
1) Вектор коллинеарен одному из векторов и , например вектору . В этом случае по лемме о коллинеарных векторах вектор можно представить в виде , где у — некоторое число, и, следовательно, т. е. вектор разложен по векторам и .
2) Вектор не коллинеарен ни вектору , ни вектору . Отметим какую-нибудь точку О и отложим от неё векторы (рис. 274). Через точку Р проведём прямую, параллельную прямой ОВ, и обозначим через A1 точку пересечения этой прямой с прямой О А. По правилу треугольника Но векторы коллинеарны соответственно векторам и , поэтому существуют такие числа х и у, что . Следовательно, , т. е. вектор разложен по векторам и .

Докажем теперь, что коэффициенты х и у разложения определяются единственным образом. Допустим, что наряду с разложением имеет место другое разложение Вычитая второе равенство из первого и используя правила действий над векторами, получаем Это равенство может выполняться только в том случае, когда коэффициенты х - х1 и у - у1 равны нулю. В самом деле, если предположить, например, что х - x1 ≠ 0, то из полученного равенства найдём а значит, векторы и коллинеарны.

Но это противоречит условию теоремы. Следовательно, х - х1 = 0 и у - у1 = 0, откуда х = х1 и у = у1. Это и означает, что коэффициенты разложения вектора определяются единственным образом. Теорема доказана.
Координаты вектора
Понятие прямоугольной системы координат (или, как иногда говорят, декартовой системы координат) нам известно из курса алгебры.
Напомним, что для задания прямоугольной системы координат нужно провести две взаимно перпендикулярные прямые, на каждой из них выбрать направление (оно обозначается стрелкой) и выбрать единицу измерения отрезков. При выбранной единице измерения отрезков длина каждого отрезка выражается положительным числом.
В дальнейшем под длиной отрезка мы будем понимать это число.
Отложим от начала координат О единичные векторы (т. е. векторы, длины которых равны единице) и так, чтобы направление вектора совпало с направлением оси Ох, а направление вектора — с направлением оси Оу (рис. 275). Векторы и назовём координатными векторами.

Координатные векторы не коллинеарны, поэтому любой вектор можно разложить по координатным векторам, т. е. представить в виде , причём коэффициенты разложения (числа х и у) определяются единственным образом. Коэффициенты разложения вектора по координатным векторам называются координатами вектора в данной системе координат. Координаты вектора будем записывать в фигурных скобках после обозначения вектора: . На рисунке 275 и .
Так как нулевой вектор можно представить в виде то его координаты равны нулю: Если векторы и равны, то х1 = х2 и у1 = у2. Таким образом, координаты равных векторов соответственно равны.
Рассмотрим правила, позволяющие по координатам векторов находить координаты их суммы, разности и произведения вектора на число.
| 1 0 . Каждая координата суммы двух или более векторов равна сумме соответствующих координат этих векторов. |
Докажем это утверждение для двух векторов. Рассмотрим векторы 1; j1> и 2; у2>. Так как и то, пользуясь свойствами сложения векторов и умножения вектора на число, получим:

Отсюда следует, что координаты вектора + равны 1 + х2; у1 + у2).
Аналогично доказывается следующее утверждение:
| 2 0 . Каждая координата разности двух векторов равна разности соответствующих координат этих векторов. |
Иными словами, если 1; у1) и 2; у2> — данные векторы, то вектор - имеет координаты 1 - х2; y1 - у2). Проведите доказательство самостоятельно.
| 3 0 . Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число. |
В самом деле, пусть вектор имеет координаты .
Рассмотренные правила позволяют определить координаты любого вектора, представленного в виде алгебраической суммы данных векторов с известными координатами. Пусть, например, требуется найти координаты вектора , если известно, что , ,
По правилу 3 0 вектор 2 имеет координаты , а вектор координаты . Так как то координаты вектора можно найти по правилу 1 0 : .

Итак, вектор имеет координаты .
Задачи
911. Найдите такое число k, чтобы выполнялось равенство если известно, что:
а) векторы противоположно направлены и ;
б) векторы сонаправлены и ;
в) векторы противоположно направлены и ;
г) векторы сонаправлены и .
912. Диагонали параллелограмма ABCD пересекаются в точке О, М — середина отрез ка АО. Найдите, если это возможно, та кое число k, чтобы выполнялось равенство:

913. Векторы и коллинеарны. Коллинеарны ли векторы: Ответ обоснуйте.
914. Докажите, что если векторы + и - не коллинеарны, то:
а) векторы и не коллинеарны;
б) векторы 2- и и не коллинеарны;
в) векторы + и + 3 не коллинеарны.
915. Точка М лежит на диагонали АС параллелограмма ABCD, причём AM : МС = 4:1. Разложите вектор по векторам .
916. Векторы и не коллинеарны. Найдите числа х и у, удовлетворяющие равенству:

917. Начертите прямоугольную систему координат Оху и координатные векторы и . Постройте векторы с началом в точке О, заданные координатами
918. Разложите векторы изображённые на рисунке 276, а, б, в, по координатным векторам и и найдите их координаты.

919. Выпишите координаты векторов



920. Запишите разложение по координатным векторам и
вектора:
921. Найдите числа х и у, удовлетворяющие условию:

922. Найдите координаты вектора - если:

923. Найдите координаты вектора + если:

924. Найдите координаты векторов если .
925. Даны векторы Найдите координаты векторов, противоположных данным.

926. Найдите координаты вектора если:

927. Докажите, что если два вектора коллинеарны, то координаты одного вектора пропорциональны координатам другого. Сформулируйте и докажите обратное утверждение.

928. Даны векторы . Укажите среди этих векторов попарно коллинеарные векторы.
Ответы к задачам
911. а) -4; б) 20; в) -1; г) 5.
912. б) 1/2; в) - 1/2; г) 1; д) -1; е) - 1/4; ж) 3; з) - 3/4 и) число k не существует.
914. Указание. Доказательство провести методом от противного и воспользоваться леммой о коллинеарных векторах.

915.
916. а) х = -1, у = 3; б) х = 4, у = -5; в) х = 0, у = 3; г) x = -1, у = 1/3.

918.

919.

920.
921. а) х=5, у = -2; б) x = -3, у = 7; в) д: = -4, у = 0; г) х = 0, у = 0.

924.
927. Указание. Воспользоваться леммой о коллинеарных векторах.

928.
1 Леммой называется вспомогательная теорема, с помощью которой доказывается следующая теорема или несколько теорем.

Сколько векторов равных данному можно отложить от точки…..

Два коллинеарных вектора направленные одинаково называются ……

Векторы называются равными ,если…..

Разложение вектора по двум неколлинеарным векторам
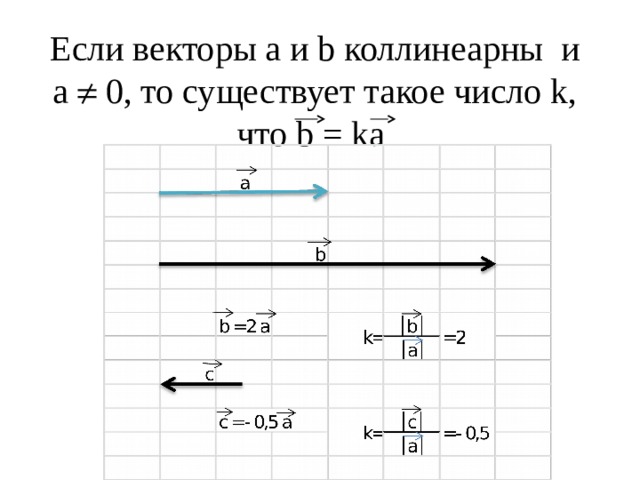
Если векторы а и b коллинеарны и а 0, то существует такое число k, что b = ka
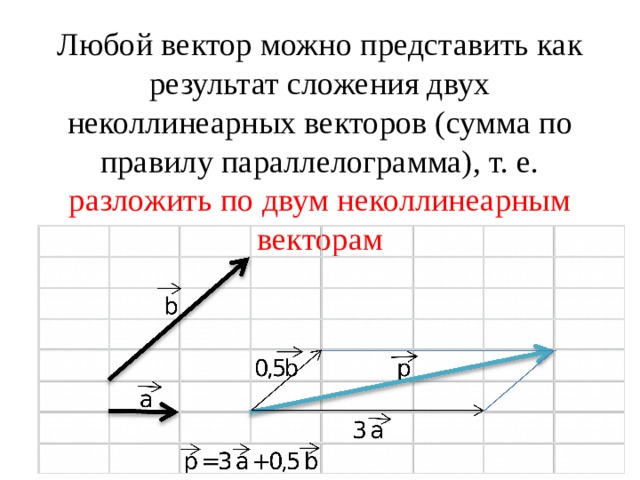
Любой вектор можно представить как результат сложения двух неколлинеарных векторов (сумма по правилу параллелограмма), т. е. разложить по двум неколлинеарным векторам
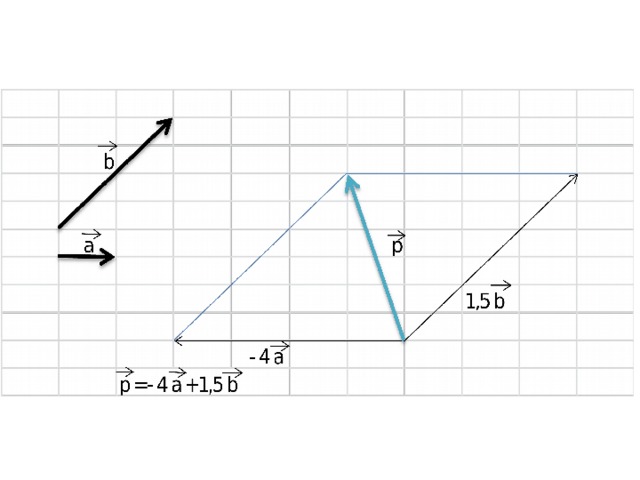

Чтобы разложить вектор по двум векторам надо: 1) отложить все три вектора от одной точки; 2) достроить до параллелограмма; 3) вычислить значения k для каждого вектора
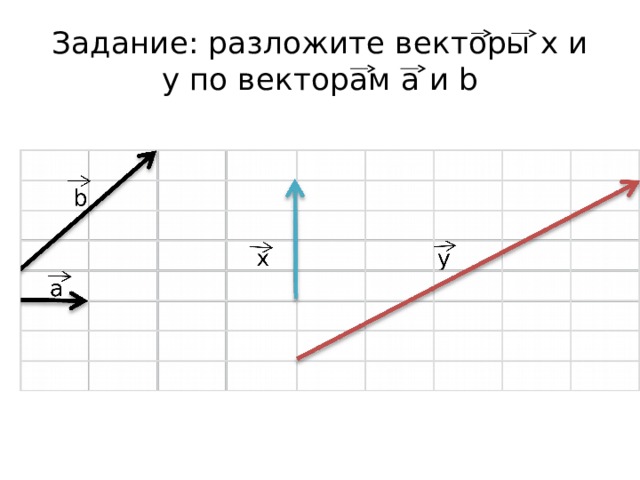
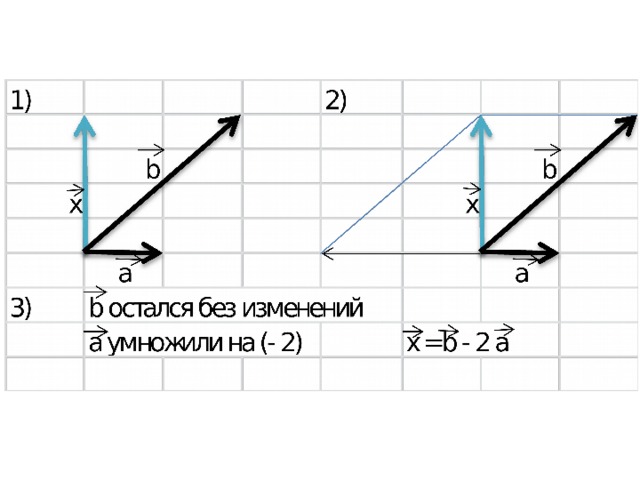
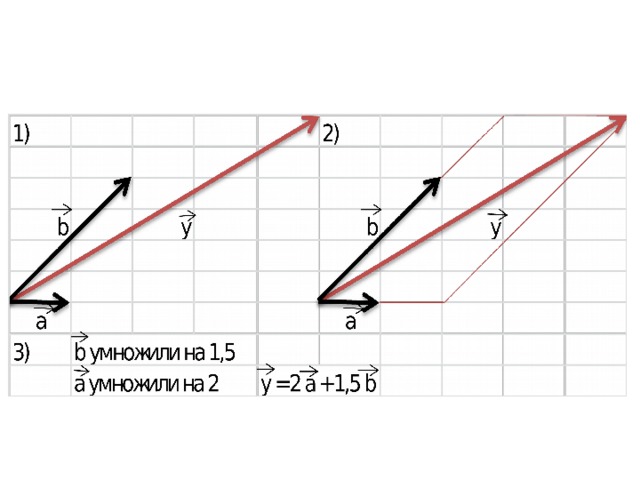
Задание: разложите векторы x и y по векторам a и b

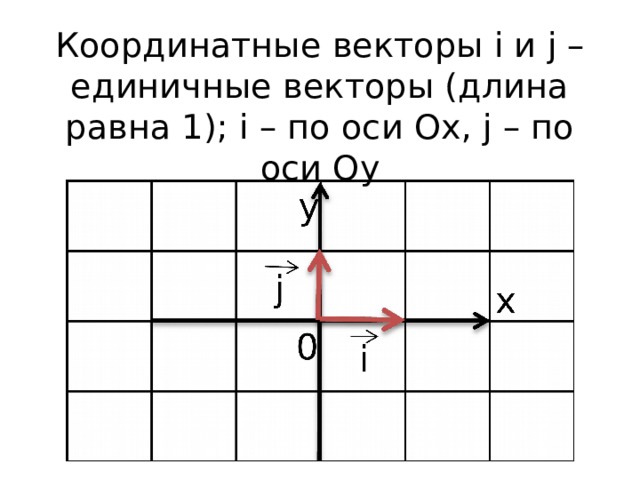
Координатные векторы i и j – единичные векторы (длина равна 1); i – по оси Ox, j – по оси Oy
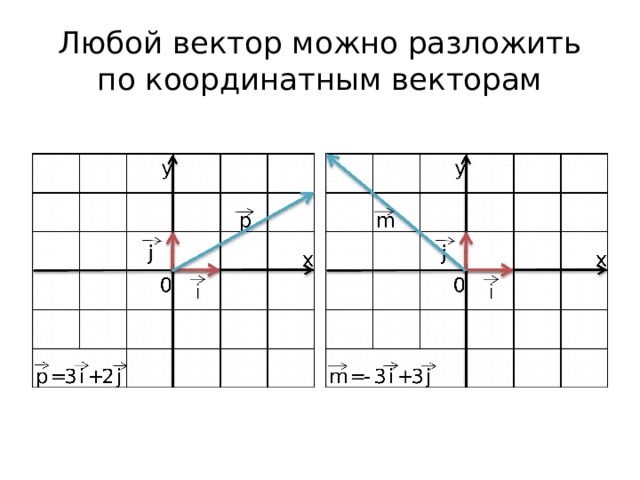
Любой вектор можно разложить по координатным векторам
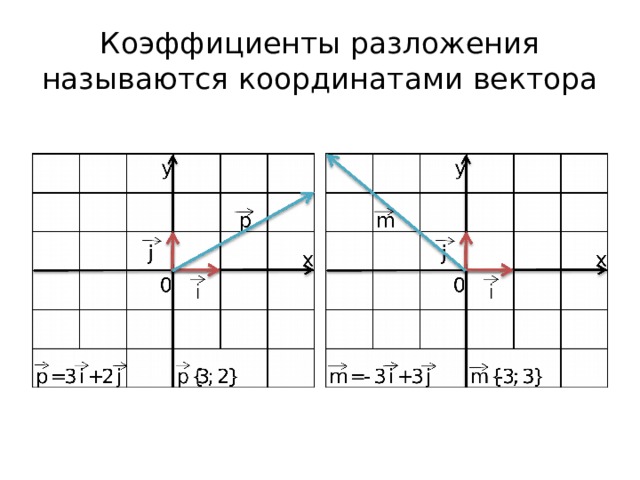
Коэффициенты разложения называются координатами вектора

1. Каждая координата суммы векторов равна сумме соответствующих координат a + b = c 2. Каждая координата разности векторов равна разности соответствующих координат a - b = c

3. Каждая координата произведения вектора на число равна произведению соответствующей координаты на это число если a , то -4 a

Задание: найти координаты вектора p = 2 a – 1/3 b + c , если a , b , c 1) 2a , 2a 2) – 1/3b <0*(-1/3); 3*(-1/3)>, - 1/3 b 3) c 4) p , p
Читайте также:

