Что такое сочетание в математике кратко

Обновлено: 05.07.2024

Комбинаторика - это раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов. Основы комбинаторики очень важны для оценки вероятностей случайных событий, т.к. именно они позволяют подсчитать принципиально возможное количество различных вариантов развития событий.

Основная формула комбинаторики

Пусть имеется k групп элементов, причем i-я группа состоит из n_i элементов. Выберем по одному элементу из каждой группы. Тогда общее число N способов, которыми можно произвести такой выбор, определяется соотношением N=n₁*n₂*n₃*. *n_k.

Пример 1. Поясним это правило на простом примере. Пусть имеется две группы элементов, причем первая группа состоит из n₁ элементов, а вторая - из n₂ элементов. Сколько различных пар элементов можно составить из этих двух групп, таким образом, чтобы в паре было по одному элементу от каждой группы? Допустим, мы взяли первый элемент из первой группы и, не меняя его, перебрали все возможные пары, меняя только элементы из второй группы. Таких пар для этого элемента можно составить n₂. Затем мы берем второй элемент из первой группы и также составляем для него все возможные пары. Таких пар тоже будет n₂. Так как в первой группе всего n₁ элемент, всего возможных вариантов будет n₁*n₂.

Пример 2. Сколько трехзначных четных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, 6, если цифры могут повторяться?
Решение: n₁=6 (т.к. в качестве первой цифры можно взять любую цифру из 1, 2, 3, 4, 5, 6), n₂=7 (т.к. в качестве второй цифры можно взять любую цифру из 0, 1, 2, 3, 4, 5, 6), n₃=4 (т.к. в качестве третьей цифры можно взять любую цифру из 0, 2, 4, 6).
Итак, N=n₁*n₂*n₃=6*7*4=168.

В том случае, когда все группы состоят из одинакового числа элементов, т.е. n₁=n₂=. n_k=n можно считать, что каждый выбор производится из одной и той же группы, причем элемент после выбора снова возвращается в группу. Тогда число всех способов выбора равно n k . Такой способ выбора в комбинаторики носит название выборки с возвращением.

Пример 3. Сколько всех четырехзначных чисел можно составить из цифр 1, 5, 6, 7, 8?
Решение. Для каждого разряда четырехзначного числа имеется пять возможностей, значит N=5*5*5*5=5 4 =625.

Рассмотрим множество, состоящие из n элементов. Это множество в комбинаторике называется генеральной совокупностью.

Число размещений из n элементов по m

Определение 1. Размещением из n элементов по m в комбинаторике называется любой упорядоченный набор из m различных элементов, выбранных из генеральной совокупности в n элементов.

Пример 4. Различными размещениями из трех элементов по два будут наборы (1, 2), (2, 1), (1, 3), (3, 1), (2, 3),(3, 2). Размещения могут отличаться друг от друга как элементами, так и их порядком.

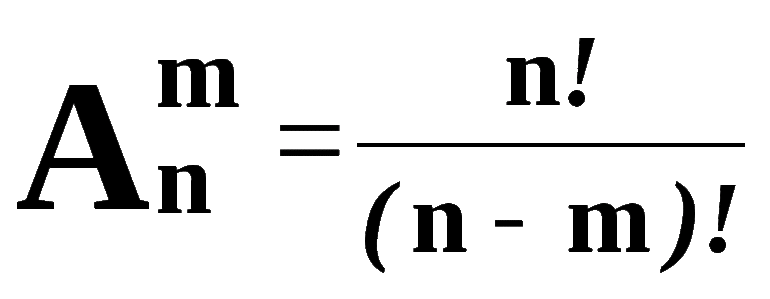
Число размещений в комбинаторике обозначается A_n m и вычисляется по формуле:

Замечание: n!=1*2*3*. *n (читается: "эн факториал"), кроме того полагают, что 0!=1.

Пример 5. Сколько существует двузначных чисел, в которых цифра десятков и цифра единиц различные и нечетные?
Решение: т.к. нечетных цифр пять, а именно 1, 3, 5, 7, 9, то эта задача сводится к выбору и размещению на две разные позиции двух из пяти различных цифр, т.е. указанных чисел будет:

Определение 2. Сочетанием из n элементов по m в комбинаторике называется любой неупорядоченный набор из m различных элементов, выбранных из генеральной совокупности в n элементов.

Пример 6. Для множества сочетаниями являются , , .

Число сочетаний из n элементов по m

Число сочетаний обозначается C_n m и вычисляется по формуле:

Пример 7. Сколькими способами читатель может выбрать две книжки из шести имеющихся?

Решение: Число способов равно числу сочетаний из шести книжек по две, т.е. равно:

Перестановки из n элементов

Определение 3. Перестановкой из n элементов называется любой упорядоченный набор этих элементов.

Пример 7a. Всевозможными перестановками множества, состоящего из трех элементов являются: (1, 2, 3), (1, 3, 2), (2, 3, 1), (2, 1, 3), (3, 2, 1), (3, 1, 2).

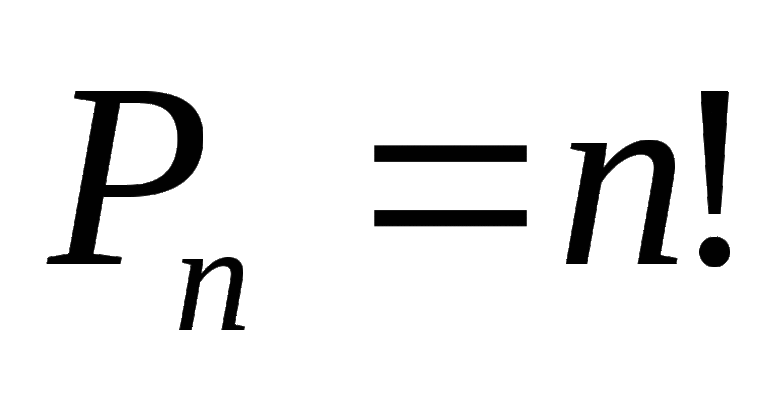
Число различных перестановок из n элементов обозначается P_n и вычисляется по формуле P_n=n!.

Пример 8. Сколькими способами семь книг разных авторов можно расставить на полке в один ряд?

Решение:эта задача о числе перестановок семи разных книг. Имеется P₇=7!=1*2*3*4*5*6*7=5040 способов осуществить расстановку книг.

Во-первых, от того, из какого количества элементов мы можем комбинировать их наборы (насколько велика генеральная совокупность элементов).

Во-вторых, результат зависит от того, какой величины наборы элементов нам нужны.

И последнее, важно знать, является ли для нас существенным порядок элементов в наборе. Поясним последний фактор на следующем примере.

Пример 9. На родительском собрании присутствует 20 человек. Сколько существует различных вариантов состава родительского комитета, если в него должны войти 5 человек?
Решение: В этом примере нас не интересует порядок фамилий в списке комитета. Если в результате в его составе окажутся одни и те же люди, то по смыслу для нас это один и тот же вариант. Поэтому мы можем воспользоваться формулой для подсчета числа сочетаний из 20 элементов по 5.

Иначе будут обстоять дела, если каждый член комитета изначально отвечает за определенное направление работы. Тогда при одном и том же списочном составе комитета, внутри него возможно 5! вариантов перестановок, которые имеют значение. Количество разных (и по составу, и по сфере ответственности) вариантов определяется в этом случае числом размещений из 20 элементов по 5.

Задачи для самопроверки
1. Сколько трехзначных четных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, 6, если цифры могут повторяться?
Т.к. число четное на третьем месте может стоять 0, 2, 4, 6, т.е. четыре цифры. На втором месте может стоять любая из семи цифр. На первом месте может стоять любая из семи цифр кроме нуля, т.е. 6 возможностей. Результат =4*7*6=168.
2. Сколько существует пятизначных чисел, которые одинаково читаются слева направо и справа налево?
На первом месте может стоять любая цифра кроме 0, т.е. 9 возможностей. На втором месте может стоять любая цифра, т.е. 10 возможностей. На третьем месте тоже может стоять любая цифра из, т.е. 10 возможностей. Четвертая и пятая цифры определены заранее, они совпадают с первой и второй, следовательно, число таких чисел 9*10*10=900.
3. В классе десять предметов и пять уроков в день. Сколькими способами можно составить расписание на один день?

4. Сколькими способами можно выбрать 4 делегата на конференцию, если в группе 20 человек?

n = C₂₀ 4 = (20!)/(4!*(20-4)!)=(16!*17*18*19*20)/((1*2*3*4)*(16!))=(17*18*19*20)/(1*2*3*4)=4845.
5. Сколькими способами можно разложить восемь различных писем по восьми различным конвертам, если в каждый конверт кладется только одно письмо?
В первый конверт можно положить 1 из восьми писем, во второй одно из семи оставшихся, в третий одно из шесть т.д. n = 8! = 1*2*3*4*5*6*7*8 = 40320.
6. Из трех математиков и десяти экономистов надо составить комиссию, состоящую из двух математиков и шести экономистов. Сколькими способами это можно сделать?

Число способов выбрать математика С₃ 2 =3!/(2!*(3-2))!=3/2, число способов выбрать экономиста С₁₀ 6 =10!/(6!*(10-6))!=7*8*9*10/(1*2*3*4)=210. n=С₃ 2 *С₁₀ 6 =3*210=630.

Сочетанием из \(n\) элементов по \(m\) элементов m ≤ n называется выборка элементов \(m\) из данного неупорядоченного множества.

1. даны \(3\) элемента .

Это можно сделать \(3\) способами — ; ; — по формуле: C 3 2 = 3 ! 2 ! ⋅ 3 − 2 ! = 3 ⋅ 2 ! 2 ! ⋅ 1 ! = 3 .

Это тоже можно сделать \(3\) способами — ; ; — по формуле: C 3 1 = 3 ! 1 ! ⋅ 3 − 1 ! = 3 ⋅ 2 ! 1 ! ⋅ 2 ! = 3 .

2. У Светланы есть \(12\) платьев. Сколькими способами из них можно выбрать \(3\) платья для поездки на курорт?

Решение:
так как порядок выбора платьев неважен, нужно вычислить сочетания по \(3\) элемента из \(12\) элементов, т. е. \(n = 12\) и \(m = 3\).

C 12 3 = 12 ! 3 ! ( 12 − 3 ) ! = 12 ! 3 ! ⋅ 9 ! = 9 ! ⋅ 10 ⋅ 11 ⋅ 12 3 ! ⋅ 9 ! = 10 ⋅ 11 ⋅ 12 1 ⋅ 2 ⋅ 3 = 1320 6 = 220 .

3. Из \(6\) человек (\(2\) женщин и \(4\) мужчин) нужно выбрать \(1\) женщину и \(2\) мужчин. Сколькими способами это можно сделать?

так как порядок выбора неважен (в конце концов команда будет той же), нужно вычислить, сколькими способами из \(2\) женщин можно выбрать \(1\), а из \(4\) мужчин — двоих.

В многогранной комбинаторике огромное значение имеет число сочетаний, а также вытекающие из этого понятия правила. Этот раздел математики занимается изучением уравнений выбора и последующего размещения задействованных элементов из общепринятого множества в соответствии с действующими нормами. Базовые формулы и принципы комбинаторики часто применяются в теории вероятностей для подсчёта случайных событий.

Краткое описание
Ключевые нюансы
Выборки и подсчёт суммы
Действующее правило произведения
Решение примеров комбинированного типа
Доступные размещения с повторениями и без них

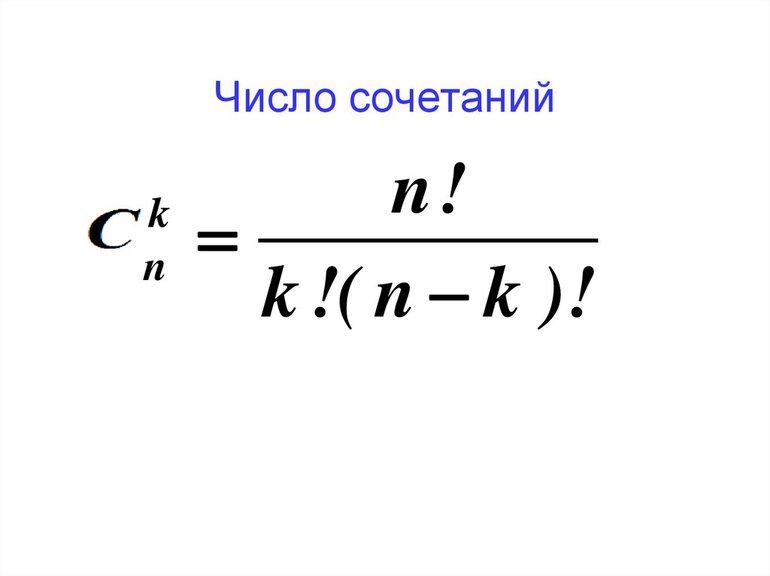
Краткое описание

Изучение математических правил не может обойти стороной число сочетаний из n по k. Формулы комбинаторики как науки активно используются во всех жизненных отраслях. Этот раздел включён в школьную программу старших классов и вступительные испытания многих вузов России. Удивительная комбинаторика лежит в основе прикладного искусства.

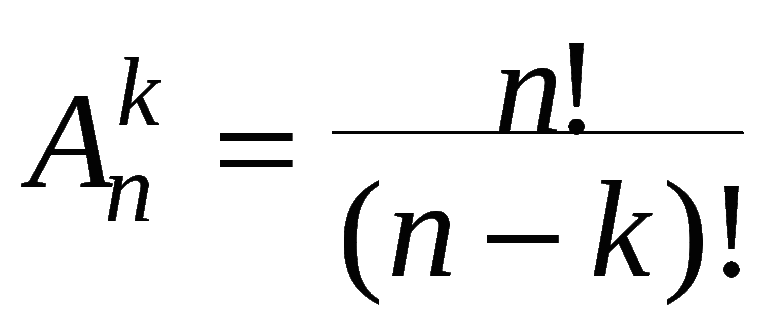
Это направление науки начало активно развиваться ещё шесть веков назад. Достоверно известно, что первые комбинаторные задачи присутствовали в трудах философов и талантливых математиков Средневековья. В те времена представители стремительно развивающегося научного мира всячески пытались найти актуальные методы решения поставленных задач, хотели определить основные правила и понятия, а также утвердить уникальные в своём роде формулы и математические уравнения для тех, кто ещё не знаком с этим научным направлением.

Актуальные формулы и нормы комбинаторики применяются в распространённой теории вероятностей, где специалисты могут быстро и качественно подсчитать процент случайных событий, чтобы в итоге получить закон реального распределения случайных величин. При правильном подходе можно углублённо изучать закономерности тех или иных событий, что очень важно для понимания статистических природных правил, которые неизбежно проявляются в окружающей природе и эксплуатируемой технике.

Ключевые нюансы

Используемое в математике число сочетаний с повторениями можно подробно изучить по книгам и специальным изданиям. Комбинаторика подробно описана в том разделе науки, который занимается многофункциональными операциями с множеством задействованных элементов.

Экспертами было доказано, что это направление затрагивает довольно большой математический пласт, в котором ученикам предлагается изучить, сколько в мире существует различных комбинаций, подчиняющихся определённым условиям. Основной задачей этой науки можно считать требование размещения различных объектов по специальным правилам и последующее нахождение точного количества способов таких расположений.

На просторах интернета можно встретить много различных учебников и другого познавательного материала по информатике/математике для школьников, а также специальные сборники уравнений и сложных примеров для студентов, где в доступном и максимально подробном виде объяснена довольно увлекательная и познавательная комбинаторика. В начальных классах задачи на эту тему решают на специальных кружках, а вот в гимназиях с углублённым изучением точных наук ей посвящают основные уроки. Многоуровневые задачи по комбинаторике включены в программу олимпиады.

Существует ряд базовых понятий, которые нужно усвоить учащимся:

Если в конкретном примере f = n, то эти размещения называются исключительно перестановками.
Размещение. В этом случае речь касается совершенно любого упорядоченного подмножества f из задействованных элементов множества n.
Сочетания. В качестве основы может быть задействовано любое подмножество из элементов f, которые принадлежат изучаемому множеству, состоящему из n — различных элементов.

Необходимо отметить тот факт, что за основу может быть взят объект или целое явление, которое попадает в искомое множество. Перестановка затрагивает элементы, которые находятся в большом количестве и определённом порядке. Сочетание — своеобразные подмножества, пребывающие в произвольной форме. Размещение представляет собой упорядоченные подмножества в исходном множестве. Правильно посчитать нужный коэффициент можно при помощи многофункциональных онлайн-калькуляторов, которые обладают всеми необходимыми функциями.

Выборки и подсчёт суммы

Если предположить, что А = — множество из n элементов, то их совокупность будет называться выборкой объёма k из n. В этом случае действует ряд важных правил. Выборка может считаться правильно упорядоченной только в том случае, если итоговая последовательность следования всех задействованных элементов в ней была задана учеником заранее. Исключений не предусмотрено.

Различными выборками называются только те математические примеры, которые отличаются исключительно порядком следования элементов. Если отличия незначительные, тогда ученику предстоит работать с неупорядоченной комбинацией. В отдельных примерах могут допускаться или не должны допускаться повторения задействованных элементов.

Чаще всего перед учащимися возникает необходимость подсчёта точного числа вероятных выборок с определёнными математическими параметрами. Довольно часто для контроля над вероятными комбинаторными объектами используется два ключевых приёма — правила произведения и суммы. На каждый случай специалисты предусмотрели ряд важных правил, которые призваны обезопасить учащегося от различных ошибок.

Базовое требование математического произведения основано на том, что когда исследуемый объект А может быть выбран различными f способами, то итоговый выбор А и B в указанном ранее порядке может быть осуществлён f * n методами. Правило суммы отличается тем, что если ученик имеет несколько возможностей выбрать точку А, тогда поиск А или В можно будет осуществить по специальной системе f + n.

Действующее правило произведения

Именно это направление в комбинаторике является одним из базовых для решения поставленных задач. При тщательном выборе элемента А из n способов (В из m) правильным считается то утверждение, в соответствии с которым одновременно подобрать пару А и В можно n * m методами, что очень важно. На этот случай действует три основных утверждения:

Если ученику на каждом новом шаге известно количество доступных вариантов выбора, то для правильного определения суммарного количества способов необходимо все имеющиеся данные перемножить между собой.
Когда есть возможность выбрать первый искомый элемент в задействованной комбинации любым a способом, а для второго примера можно применить вариант d, то общее число действий будет соответствовать формуле a * b. Это утверждение является наиболее распространённым.
Если k способами можно безошибочно выбрать элемент x, а для Y подойдут имеющиеся m методы, тогда для пары x и y выполняется расчёт по формуле k * m. Данные можно записать в виде таблицы.

В эффективности описанных правил можно убедиться, благодаря некоторым примерам. По условиям задачи дано два ромба, три мяча, четыре гантели и пять кубов. Ученику нужно определить, сколькими способами можно будет вытянуть ромб, мяч, гантель и куб. Решение элементарное: 2*3*4*5= 120. Стоит отметить, что в этой задаче может быть задействован факториал, с помощью которого всегда можно вычислить более сложные варианты и решить трудные задачи.

По условиям следующего примера дано два мяча и пять скакалок. Задача состоит в том, чтобы определить, какова вероятность достать 1 скакалку и 1 мяч. Решение: 2*5=10.

Решение примеров комбинированного типа

Специфический магический квадрат. По условиям необходимо отыскать фигуру, в которой итоговая сумма всех задействованных чисел в столбцах и рядах будет одинакова (основной тип — латинский квадрат). Для решения таких уравнений понадобятся рекуррентные соотношения. А вот для поиска правильного ответа придётся задействовать гораздо меньше элементов, которые применяются в востребованных формулах и правилах.
Математические задачи про торговцев. Суть состоит в том, чтобы отыскать все реальные способы прохождения людей из стартового пункта A в точку B. В этом случае действует метод траектории. Для этой разновидности задач свойственно элементарное геометрическое проектирование возможных способов решения.
Математические примеры с размещением. Классическая производственная задача (к примеру, используется в лоскутной методике) — отыскать все доступные способы разложения некоторого количества задействованных элементов в специальные ячейки, но только в чётком порядке. В этом случае действуют включения и исключения. Этот вариант применяется специалистами при доказательстве различных выражений.

Экспертами неоднократно было подтверждено, что комбинаторика является интересной и познавательной наукой, так как в наш век быстрой модернизации инновационных технологий постоянно будут нужны профессиональные специалисты, которые способны в полном объёме предоставить разнообразные решения для тех или иных практических задач.

Доступные размещения с повторениями и без них

Работа с различными математическими комбинациями подразумевает использование определённых правил, в противном случае избежать распространённых ошибок будет крайне сложно. Если имеющаяся l различных элементов может повториться m раз, оказавшись на имеющихся m местах, тогда при составлении вывода количество размещений с последующими повторениями вычисляется по определённой комбинаторной формуле — Am / l = l m . Именно под этим определением принято понимать чёткий набор компонентов m из множества l: A m/l = l * (l-1) * (l -2) *… * (l—m +1) = l!/(l—m)!.

Изучаемое число сочетаний без повторений сопряжено с некоторыми дополнительными нюансами. В этом случае в распоряжении учащегося имеется n разных математических элементов. Многих в такой ситуации интересует, сколько именно можно будет составить актуальных k расстановок.

Два базовых подхода считаются различными только при условии, если они отличаются друг от друга минимум одним элементом или состоят из аналогичных элементов, которые расположены в разном порядке. Каждый нюанс должен быть учтён, так как от этого зависит итоговый результат.

Описанные правила и формулы позволяют решать довольно сложные и многоуровневые задачи. К примеру, из трёх предъявленных цифр нужно выбрать только две, чтобы в итоге получились разные двузначные числа. По условиям описанной задачи нужно определить, сколько вариантов существует в этом случае. Ответ: (4а) А2/3=3*2 = 6. Но также уместно следующее решение: А2/3 = 3!/(3−2)! = 3!/1! = 1*2*3/1 = 6. В этом случае каждый существующий элемент может быть расположен по несколько раз, что соответствует условиям задачи. Для этой ситуации уместна следующая формула: (5) Ak / l = l k .

Комбинаторика – раздел математики, который изучает задачи выбора и расположения элементов из некоторого основного множества в соответствии с заданными правилами. Формулы и принципы комбинаторики используются в теории вероятностей для подсчета вероятности случайных событий и, соответственно, получения законов распределения случайных величин. Это, в свою очередь, позволяет исследовать закономерности массовых случайных явлений, что является весьма важным для правильного понимания статистических закономерностей, проявляющихся в природе и технике.

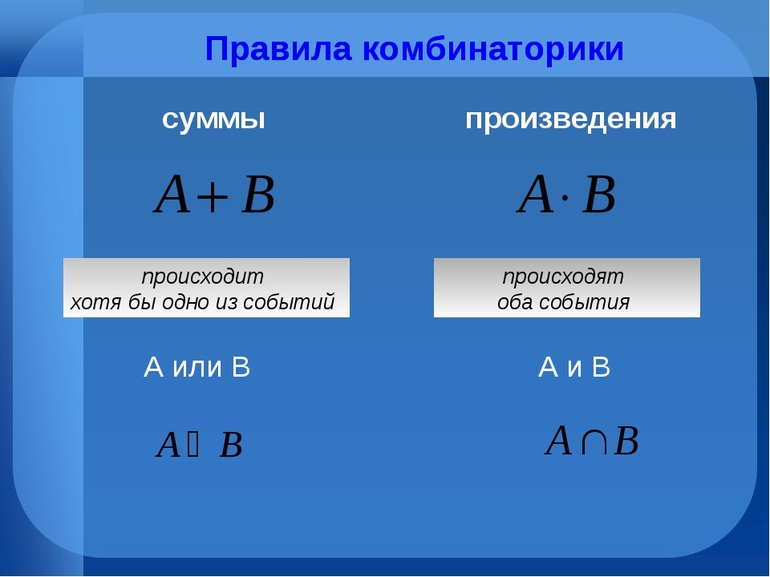
Правила сложения и умножения в комбинаторике

Правило суммы. Если два действия А и В взаимно исключают друг друга, причем действие А можно выполнить m способами, а В – n способами, то выполнить одно любое из этих действий (либо А, либо В) можно n + m способами.

Пример 1.

В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить одного дежурного?

Дежурным можно назначить либо мальчика, либо девочку, т.е. дежурным может быть любой из 16 мальчиков, либо любая из 10 девочек.

По правилу суммы получаем, что одного дежурного можно назначить 16+10=26 способами.

Правило произведения. Пусть требуется выполнить последовательно k действий. Если первое действие можно выполнить n₁ способами, второе действие n₂ способами, третье – n₃ способами и так до k-го действия, которое можно выполнить n_k способами, то все k действий вместе могут быть выполнены:

Пример 2.

В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить двух дежурных?

Первым дежурным можно назначить либо мальчика, либо девочку. Т.к. в классе учится 16 мальчиков и 10 девочек, то назначить первого дежурного можно 16+10=26 способами.

После того, как мы выбрали первого дежурного, второго мы можем выбрать из оставшихся 25 человек, т.е. 25-ю способами.

По теореме умножения двое дежурных могут быть выбраны 26*25=650 способами.

Сочетания без повторений. Сочетания с повторениями

Классической задачей комбинаторики является задача о числе сочетаний без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать m из n различных предметов ?

Пример 3.

Необходимо выбрать в подарок 4 из 10 имеющихся различных книг. Сколькими способами можно это сделать?

Нам из 10 книг нужно выбрать 4, причем порядок выбора не имеет значения. Таким образом, нужно найти число сочетаний из 10 элементов по 4:

Рассмотрим задачу о числе сочетаний с повторениями: имеется по r одинаковых предметов каждого из n различных типов; сколькими способами можно выбрать m () из этих (n*r) предметов?

Пример 4.

В кондитерском магазине продавались 4 сорта пирожных: наполеоны, эклеры, песочные и слоеные. Сколькими способами можно купить 7 пирожных?

Т.к. среди 7 пирожных могут быть пирожные одного сорта, то число способов, которыми можно купить 7 пирожных, определяется числом сочетаний с повторениями из 7 по 4.

Размещения без повторений. Размещения с повторениями

Классической задачей комбинаторики является задача о числе размещений без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать и разместить по m различным местам m из n различных предметов?

Пример 5.

В некоторой газете 12 страниц. Необходимо на страницах этой газеты поместить четыре фотографии. Сколькими способами можно это сделать, если ни одна страница газеты не должна содержать более одной фотографии?

В данной задаче мы не просто выбираем фотографии, а размещаем их на определенных страницах газеты, причем каждая страница газеты должна содержать не более одной фотографии. Таким образом, задача сводится к классической задаче об определении числа размещений без повторений из 12 элементов по 4 элемента:

Таким образом, 4 фотографии на 12 страницах можно расположить 11880 способами.

Также классической задачей комбинаторики является задача о числе размещений с повторениями, содержание которой можно выразить вопросом: сколькими способами можно выбрать и разместить по m различным местам m из n предметов, среди которых есть одинаковые?

Пример 6.

У мальчика остались от набора для настольной игры штампы с цифрами 1, 3 и 7. Он решил с помощью этих штампов нанести на все книги пятизначные номера– составить каталог. Сколько различных пятизначных номеров может составить мальчик?

Можно считать, что опыт состоит в 5-кратном выборе с возращением одной из 3 цифр (1, 3, 7). Таким образом, число пятизначных номеров определяется числом размещений с повторениями из 3 элементов по 5:

Перестановки без повторений. Перестановки с повторениями

Классической задачей комбинаторики является задача о числе перестановок без повторения, содержание которой можно выразить вопросом: сколькими способами можно разместить n различных предметов на n различных местах?

Пример 7.

Для случая, когда среди выбираемых n элементов есть одинаковые (выборка с возвращением), задачу о числе перестановок с повторениями можно выразить вопросом: сколькими способами можно переставить n предметов, расположенных на n различных местах, если среди n предметов имеются k различных типов (k

Пример 8.

Читайте также: