Что такое метод монжа кратко

Обновлено: 30.06.2024

Монж впервые дал научное обоснование общего метода построения изображений, предложив рассматривать плоский чертёж, состоящий из двух проекций, как результат совмещения двух взаимно перпендикулярных плоскостей проекций. Для получения изображений предметов на чертежах Монж предложил использовать метод параллельного прямоугольного проецирования на взаимно перпендикулярные плоскости проекций (фронтальная плоскость проекций V, горизонтальная плоскость проекций H, профильная плоскость проекций W).Плоскости проекций, пересекаясь в пространстве, делят его на восемь частей, которые называются октантами. Три взаимно перпендикулярные плоскости проекций делят пространство на восемь подпространств – октантов. Для получения изображения предмет располагают в 1-ой октанте между наблюдателями и плоскостями проекций. Плоскости проекций пересекаются между собой по линиям, которые называются осями проекций. Эти оси пересекаются в точке О- точке начала координат. Оси проекций принимают за оси координат – натуральной системой прямоугольных координат. Две взаимно перпендикулярные плоскости проекций делят пространство на четыре подпространства - четверти.

Прямые общего положения. Следы прямой

Прямые общего положения не параллельны, а соответственно, и не перпендикулярны плоскостям проекций H, V и W. Поэтому на чертеже их проекции не параллельны и не перпендикулярны осям проекций Х, У и Z и искажают натуральную величину этих прямых.

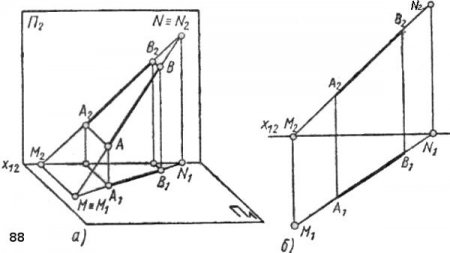
Теорема о принадлежности точки прямой: если точка принадлежит прямой, то на чертеже проекции точки лежат на одноименных проекциях прямой. Следы прямой называются точки ее пересечения с плоскостями проекций.

Вопрос Плоскость общего положения и ее проекции

Плоскость общего положения.Плоскость а, наклонная ко всем плоскостям проекций, называется плоскостью общего положения (фиг.223,а).

Особенностью этой плоскости является то, что всякая кривая и фигура, лежащие в этой плоскости, при проектировании не имеют ни одной проекции, равной натуральной (истинной) величине. Все ее следы k, L и m наклонены к осям х, z и у, замыкаясь, образуют фигуру треугольника, называемого треугольником следов. Такую плоскость можно изображать проекциями ее следов.

Образование поверхности. Определитель поверхности. Каркас поверхности.

Поверхность- совокупность всех последовательных положений перемещающейся в пространстве линии по определенному закону. Этот подход предполагает формирование поверхности в результате перемещения одной кривой U (образующей) по другой кривой V (направляющей) в соответствии с рисунком 1.

Рисунок 1 .Поверхность будет определена, если возможно в любой момент движения образующей знать ее положение и форму. Наложение условий на форму образующей линии, направляющей линии, закон перемещения образующей позволяет формировать практически любые поверхности.Описанный способ образования поверхности называется кинематическим. Другим способом образования поверхности и ее изображения на чертеже является задание поверхности множеством принадлежащих ей точек или линий. Точки и линии выбирают так, чтобы они давали возможность с достаточной степенью точности определять форму поверхности и решать на ней метрические и позиционные задачи. Множество точек или линий, определяющих поверхность, называют ее каркасом. Каркасы подразделяются на точечные и линейчатые, в соответствии с рисунком 2.

Рисунок 2. Линейным каркасом называется множество линий, имеющих единый закон образования и связанных между собой определенной зависимостью. Закон образования линии каркаса называется законом каркаса. Зависимость, устанавливающая связь между его линиями называется зависимостьюкаркаса. Зависимость каркаса характеризуется некоторой изменяемой величиной - параметром каркаса. Линейный каркас считается непрерывным, если параметр каркаса – непрерывная функция, и дискретным – в противном случае.Определитель поверхности.При задании поверхностей кинематическим способом образованияиспользуют понятие определителя. Определитель – это совокупностьнезависимых условий, однозначно задающих поверхность.В число условий, входящих в состав определителя включаются:1) геометрические фигуры (точки, линии, поверхности), с помощьюкоторых образуется поверхность;2) алгоритм формирования поверхности из данных геометрическихфигур со сведениями о характере формы образующей и законе ееперемещения.Структурная формула произвольной поверхности имеет следующий вид:Ф (Г) [A], (1)где (Г) – геометрическая часть;[A] – алгоритмическая часть.В определителе указываются параметры формы и положения. Кпараметрам формы относится величина радиуса сферы R. Задавая число,указывающее значение R, мы определяем единственную сферу. Дляконической поверхности вращения параметром может служить угол ϕмежду образующей и осью конической поверхности.Число параметров, характеризующих форму поверхности, может бытьлюбым целым положительным числом, начиная с нуля. Число параметров,характеризующих положение поверхности в пространстве, не может бытьменьше трех и больше шести. Для плоскости оно равно трем, для эллипсоидашести.Ввиду того, что поверхность может быть образована различнымиспособами, то одна и та же поверхность может иметь различныеопределители. Например: поверхность прямого кругового цилиндра скинематической точки зрения можно представить:1) как след, оставленный в пространстве прямой апри ее вращениивокруг оси m. При этом прямая азадает образующую, а ось mи словесноедобавление поясняет, что цилиндрическая поверхность являетсяповерхностью вращения, в соответствии с рисунком 4 а;2) как поступательное перемещение окружности с, при этом центрокружности Оперемещается вдоль оси m, а ее плоскость все время остаетсяперпендикулярно к этой оси, в соответствии с рисунком 4 б;3) как огибающую всех положений сферической поверхности рпостоянного радиуса, центр которой перемещается по оси m, в соответствиис рисунком 4 в.Все рассмотренные способы задания поверхности связаны между собойи при решении задач приходится переходить от одного способа задания кдругому.

Рисунок 4

а) Ф (а, m) [А1] б) Ф (с, m) [А2] в) Ф (р, m) [А3]

Образование поверхности вращения. Очерк поверхности.

Рис. 3.15

Поверхности вращения имеют весьма широкое применение во всех областях техники. Поверхностью вращения называют поверхность, получающуюся от вращения некоторой образующей линии 1 вокруг неподвижной прямой i - оси вращения поверхности (рис.3.15). На чертеже поверхность вращения задается своим очерком. Очерком поверхности называются линии, которые ограничивают области ее проекций. При вращении каждая точка образующей описывает окружность, плоскость которой перпендикулярна оси. Соответственно, линия пересечения поверхности вращения плоскостью, перпендикулярной оси, является окружностью. Такие окружности называют параллелями (рис. 3.15). Параллель наибольшего радиуса называют экватором, наименьшего - горлом. Плоскость, проходящую через ось поверхности вращения, называют меридиональной, линию ее пересечения с поверхностью вращения - меридианом. Меридиан, лежащий в плоскости, параллельной плоскости проекций, называют главным меридианом. В практике выполнения чертежей наиболее часто встречаются следующие поверхности вращения: цилиндрическая, коническая, сферическая, торовая.

Рис. 3.16

Цилиндрическую поверхность вращения. В качестве направляющей а следует взять окружность, а в качестве прямой b - ось i (рис.3.16). Тогда получим, что образующая l, параллельная оси i, вращается вокруг последней. Если ось вращения перпендикулярна горизонтальной плоскости проекций, то на П₁ цилиндрическая поверхность проецируется в окружность, а на П₃ - в прямоугольник. Главным меридианом цилиндрической поверхности являются две параллельные прямые.

Рис 3.17

Коническую поверхность вращения получим, вращая прямолинейную образующую l вокруг оси i. При этом образующая l пересекает ось i в точке S, называемой вершиной конуса (рис.3.17). Главным меридианом конической поверхности являются две пересекающиеся прямые. Если в качестве образующей взять отрезок прямой, а ось конуса перпендикулярной П₁, то на П₁коническая поверхность проецируется в круг, а на П₂ - в треугольник.

Сферическая поверхность образуется за счет вращения окружности вокруг оси, проходящей через центр окружности и лежащей в ее плоскости (рис.3.18). Экватор и меридианы сферической поверхности являются равными между собой окружностями. Поэтому при ортогональном проецировании на любую плоскость сферическая поверхность проецируется в круги.

Рис. 3.18 При вращении окружности вокруг оси, лежащей в плоскости этой окружности, но не проходящей через ее центр, образуется поверхность, называемая торовой (рис.3.19).

Рис. 3.19

11.ПОЗИЦИОННЫЕ ЗАДАЧИ.ПРИНАДЛЕЖНОСТЬ ТОЧКИ, ЛИНИИ ПОВЕРХНОСТИ.ТЕОРЕМА МОНЖА. Под позиционными подразумеваются задачи, решение которых позволяет получить ответ о принадлежности элемента (точки) или подмножества (линии) множеству (поверхности). К позиционным относятся также задачи на определение общих элементов, принадлежащих различным геометрическим фигурам. Первая группа задач может быть объединена под общим названием задачи на принадлежность. К ним, в частности, относятся задачи на определение:1) принадлежности точки линии ;2) принадлежности точки поверхности ;3) принадлежности линии поверхности .Ко второй группе относятся задачи на пересечение. Эта группа содержит также три типа задач:1) на пересечение линии с линией ;2) на пересечение поверхности с поверхностью;3) на пересечение линии с поверхностью. Принадлежность точки поверхности. Основное положение при решении задач для этого варианта принадлежности следующее: точка принадлежит поверхности, если она принадлежит какой-либо линии этой поверхности. В этом случае линии надо выбирать наиболее простыми, чтобы легче было построить проекции такой линии, затем использовать то обстоятельство, что проекции точки, лежащие на поверхности, должны принадлежать одноименным проекциям линии этой поверхности. Пример решение этой задачи показан на рисунке. Здесь есть два пути решения, поскольку можно провести две простейших линии, принадлежащих конической поверхности. В первом случае — проводится прямая линия - образующая конической поверхности S1 так, чтобы она проходила через какую-либо заданную проекцию точки С. Тем самым предполагаем, что точка С принадлежит образующей S1 конической поверхности, а следовательно - самой конической поверхности. В этом случае одноименные проекции точки С должны лежать на соответствующих проекциях этой образующей.Другая простейшая линия - окружность с диаметром 1-2 (радиус этой окружности - отсчитывается от оси конуса до очерковой образующей). Этот факт известен еще из школьного курса геометрии: при пересечении кругового конуса плоскостью, параллельной его основанию, или перпендикулярной к его оси, в сечении будет получаться окружность. Второй способ решения позволяет найти недостающую проекцию точки С, заданной своей фронтальной проекцией, принадлежащей поверхности конуса и совпадающей на чертеже с осью вращения конуса, без построения третьей проекции. Всегда следует иметь в виду, видима или не видима точка, лежащая на поверхности конуса (в случае, если она не видна, соответствующая проекция точки будет заключена в скобки). Очевидно, что в нашей задаче точка С принадлежит поверхности, поскольку проекции точки принадлежат одноимённым проекциям линий, использованных для решения как при первом, так и при втором способе решения. Принадлежность линии поверхности. Основное положение: линия принадлежит поверхности, если все точки линии принадлежат заданной поверхности. Это означает, что в данном случае принадлежности должна быть несколько раз решена задача о принадлежности точки поверхности. Торема Монжа :если две поверхности второго порядка описаны около третьей или вписаны в неё, то линия их пересечения распадается на две кривые второго порядка, плоскости которых проходят через прямую, соединяющую точки пересечения окружности касания.

12.СЕЧЕНИЯ КОНУСА ВРАЩЕНИЯ ПРОЕЦИРУЮЩИМИ ПЛОСКОСТЯМИ.При пересечении поверхностей тел проецирующими плоскостями, одна проекция сечения совпадает с проекцией проецирующей плоскости. Конус может иметь в сечении пять различных фигур. Треугольник - если секущая плоскость пересекает конус через вершину по двум образующим.Окружность - если плоскость пересекает конус параллельно основанию (перпендикулярно оси).Эллипс - если плоскость пересекает все образующие под некоторым углом. Параболу - если плоскость параллельна одной из образующих конуса. Гиперболу - если плоскость параллельна оси или двум образующим конуса. Сечение поверхности плоскостью представляет собой плоскую фигуру, ограниченную замкнутой линией, все точки которой принадлежат как секущей плоскости, так и поверхности. При пересечении плоскостью многогранника в сечении получается многоугольник с вершинами, расположенными на ребрах многогранника. Пример. Построить проекции линии пересечения L поверхности прямого кругового конуса ω плоскостью β. Решение. В сечении получается парабола, вершина которой спроецируется в точку А (А′, А′′). Точки A, D, E линии пересечения являются экстремальными. На рис. построение искомой линии пересечения осуществлено с помощью горизонтальных плоскостей уровня αi, которые пересекают поверхность конуса ω по параллелям рi , а плоскость β - по отрезкам фронтально проецирующих прямых. Линия пересечения L полностью видима на плоскостях.

№13.Соосные поверхности. Метод концентрических сфер.

При построении линии пересечения поверхностей особенности пересечения соосных поверхностей вращения позволяют в качестве вспомогательных поверхностей-посредников использовать сферы, соосные с данными поверхностями. К соосным поверхностям вращения относятся поверхности, имеющие общую ось вращения. На рис. 134 изображены соосные цилиндр и сфера (рис. 134, а), соосные конус и сфера (рис. 134, б) и соосные цилиндр и конус (рис. 134, в)

.Соосные поверхности вращения всегда пересекаются по окружностям, плоскости которых перпендикулярны оси вращения. Этих общих для обеих поверхностей окружностей столько, сколько существует точек пересечения очерковых линий поверхностей. Поверхности на рис. 134 пересекаются по окружностям, создаваемым точками 1 и 2 пересечения их главных меридианов. Вспомогательная сфера-посредник пересекает каждую из заданных поверхностей по окружности, в пересечении которых получаются точки, принадлежащие и другой поверхности, а значит, и линии пересечения. Если оси поверхностей пересекаются, то вспомогательные сферы проводят из одного центра-точки пересечения осей. Линию пересечения поверхностей в этом случае строят способом вспомогательных концентрических сфер. При построении линии пересечения поверхностей для использования способа вспомогательных концентрических сфер необходимо выполнение следующих условий:1) пересечение поверхностей вращения;2) оси поверхностей — пересекающиеся прямые — параллельны одной из плоскостей проекций, т. е. имеется общая плоскость симметрии;3) нельзя использовать способ вспомогательных секущих плоскостей, так как они не дают графически простых линий на поверхностях. Обычно способ вспомогательных сфер используется в сочетании со способом вспомогательных секущих плоскостей. На рис. 135 построена линия пересечения двух конических поверхностей вращения с пересекающимися во фронтальной плоскости уровня Ф (Ф1) осями вращения. Значит, главные меридианы этих поверхностей пересекаются и дают в своем пересечении точки видимости линии пересечения относительно плоскости П2 или самую высокую А и самую низкую В точки. В пересечении горизонтального меридиана h и параллели h', лежащих в одной вспомогательной секущей плоскости Г(Г2), определены точки видимости С и D линии пересечения относительно плоскости П1. Использовать вспомогательные секущие плоскости для построения дополнительных точек линии пересечения нецелесообразно, так как плоскости, параллельные Ф, будут пересекать обе поверхности по гиперболам, а плоскости, параллельные Г, будут давать в пересечении поверхностей окружности и гиперболы. Вспомогательные горизонтально или фронтально проецирующие плоскости, проведенные через вершину одной из поверхностей, будут пересекать их по образующим и эллипсам. В данном примере выполнены условия, позволяющие применение вспомогательных сфер для построения точек линии пересечения. Оси поверхностей вращения пересекаются в точке О (О1; О2), которая является центром вспомогательных сфер, радиус сферы изменяется в пределах Rmin

§ 12. Прямоугольное проецирование на две плоскости проекций. Метод Монжа

Прямоугольное проецирование на две плоскости проекций. Метод Монжа

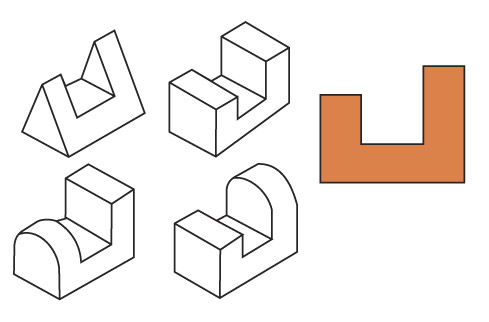
Одна проекция не всегда однозначно определяет форму изображаемого предмета. Различные по форме предметы могут образовывать одинаковые проекции (см. р ис. вверху справа).

Проецирование на две плоскости проекций. Для того чтобы получить представление о форме объемного предмета, проецирование выполняют на две плоскости проекций: горизонтальную Н и фронтальную V (рис. 42).
Плоскости проекций Н и V в пространстве размещают под прямым углом друг к другу. Линию пересечения этих плоскостей (ее обозначают х) называют осью проекций

Чтобы получить чертеж предмета на плоскости, обе плоскости Н и V совмещают в одну. Для этого горизонтальную плоскость проекций поворачивают на угол 90° так, чтобы она совпала с фронтальной плоскостью проекций. Плоскости проекций пересекаются осью проекций х (рис. 43, а).

Помните! При построении чертежа горизонтальную проекцию предмета Н всегда располагают под фронтальной V (рис. 43, б). Соединяют эти проекции линиями проекционной связи, которые являются проекциями проецирующих лучей.

Определите, какая проекция предмета является горизонтальной, а какая фронтальной. Свой ответ объясните.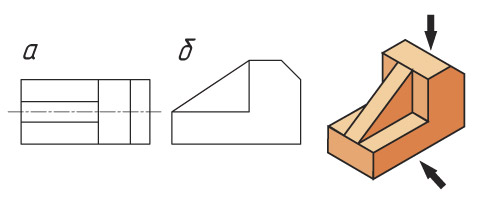

Памятка 6. Алгоритм построения двухпроекционного
комплексного чертежа детали

Для того чтобы облегчить понимание последовательности проецирования на две плоскости проекций, построение двухпроекционного чертежа детали будет
показано на бумаге в клетку

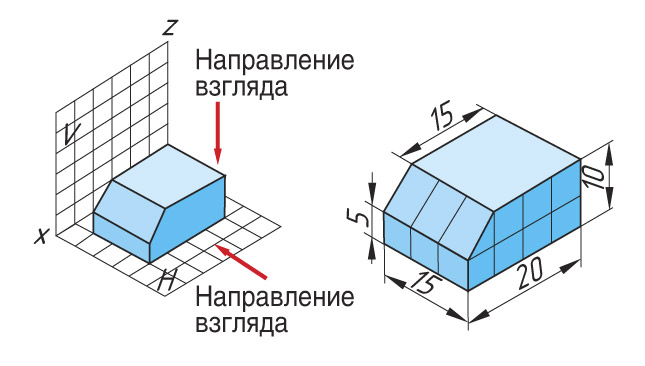
Сначала выполняется проецирование детали на фронтальную плоскость V. На наглядном изображении эта грань окрашена в голубой цвет
1. В соответствии с размерами проводятся вспомогательные линии
2. Сплошной основной толстой линией обозначается контур детали

3. Чтобы проекции находились одна под другой, проводятся линии проекционной связи, перпендикулярные к оси х, и определяется длина детали

4. Затем выполняется проецирование детали на фронтальную плоскость Н (светло-голубая плоская и голубая наклонная грани). Они имеют одинаковую ширину. Ширина детали 15 мм, ее ограничивают по бокам две грани голубого цвета, которые при взгляде сверху будут проецироваться в прямую линию

5. Если посмотреть сверху на деталь, то можно увидеть две грани под углом (голубую и светло-голубую), которые разделяет линия. Опускается соответствующая линия проекционной связи с фронтальной проекции на горизонтальную
6. Обводятся контуры детали сплошной основной толстой линией
7. Наносится осевая линия и проставляются размеры детали

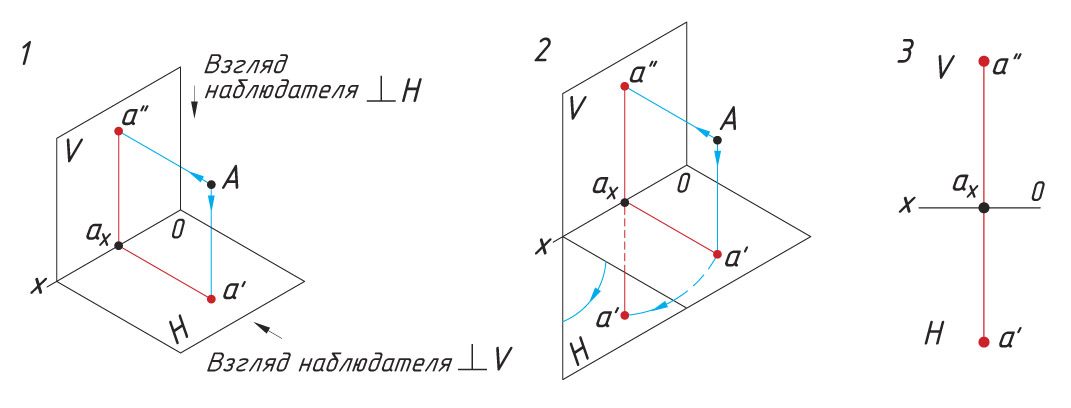
1. Из точки А на плоскости V и H опускают перпендикуляры и получают проекции точки А: а′ — горизонтальная проекция и а″ — фронтальная проекция.
2. Мысленно удаляют точку А и поворачивают плоскость Н вокруг оси Ох на угол 90° вниз до совмещения с плоскостью V.
3. Проекции а′ и а″ расположились на одной прямой а′а″. Линия а′а″ называется линией проекционной связи.

Помните! Фронтальная и горизонтальная проекции точки всегда находятся на перпендикуляре к оси проекций ох.
Отрезок а′ах — расстояние точки А до плоскости V. Отрезок а″ах — расстояние точки А до плоскости Н.

Основы начертательной геометрии возникли еще в глубокой древности. Греческий геометр Евклид и римский архитектор Витрувий внесли большой вклад в развитие методов построения изображений пространственных форм на плоскости. Бурное развитие архитектуры, живописи и скульптуры в эпоху Возрождения создало условия для развития методов построения изображений пространственных форм на плоскости. В это время вводится целый ряд основных понятий: центральное проецирование, картинная плоскость, дистанция, главная точка, линия горизонта, дистанционные точки и т. д. Одним из первых, кто применял перспективу в своих работах, был итальянский архитектор и ученый Ф. Брунеллески. В трактате по перспективе Леонардо да Винчи приводятся примеры применения перспективных изображений, сведения о воздушной и линейной перспективе и теории светотени. Большой вклад в теорию перспективы внесли Альбрехт Дюрер, Гвидо Убальди, Жерар Дезарг. Но только в 1798 г. французский инженер и ученый Гаспар Монж сформулировал главные элементы теории построения графических изображений.

Если предмет пространства спроецировать на 2 или 3 взаимно перпендикулярные плоскости, то такой метод проецирования называется методом Монжа (по имени его автора - французского ученого Гаспара Монжа).

π₁ – горизонтальная плоскость проекций

π₂ – фронтальная плоскость проекций

π₃ – профильная плоскость проекций

В пересечении плоскостей получаем оси координат х, у, z. Точку пересечения координат называют началом координат О или центром проекций.

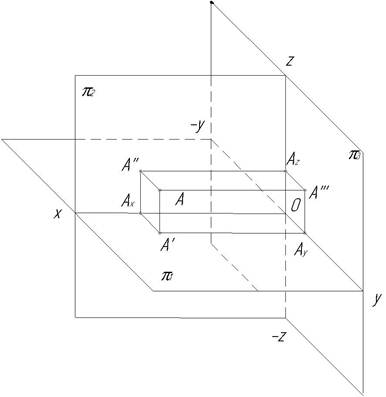
Из (•) А опускаем _┴ на 3 плоскости и получаем проекции точки на этих плоскостях:

А' - горизонтальная проекция (•) А

А" - фронтальная проекция (•) А

A"' - профильная проекция (•) А

Расстояния от (•) А до плоскостей проекций называют координатами точки. Масштаб по осям Ох и Оz - 1:1, по оси Оу – 1:2. Для определения положения точки в пространстве необходимы ее три прямоугольные координаты или две ее ортогональные проекции (рис. 6).

Совместим плоскость π₁ с π₂ и π₃ сπ₂ путем вращения вокруг осей Ох и Оz, получим плоское изображение точки - эпюр. Такое плоское изображение точки показано на рис.7.

При построении (•) на эпюре горизонтальная проекция А' характеризуется координатами х, у;

фронтальная А" – х, z;

профильная A"' - у, z.

На эпюре горизонтальная и фронтальная проекция (•) находятся на одном _┴ к оси Ox (А'А" _┴ Оx ), фронтальная и профильная проекции точки находятся на одном _┴ к оси Oz (А"A"' _┴ Oz), т.к. это плоский чертеж, искажения по осям Ox, Oy, Oz нет. Геометрическая связь между тремя проекциями точки позволяет находить третью проекцию по двум заданным графически - при помощи линий проекционной связи, а также путем измерения координат.

Пример 1. По двум заданным проекциям точек А, В, С построить третью. Построить наглядные изображения точек (рис.8).

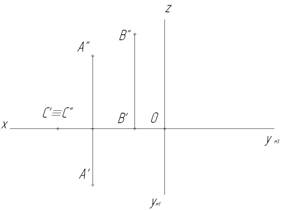
Рис.8

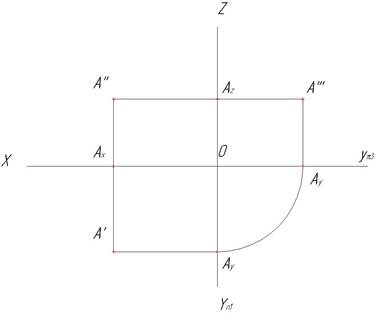
1. На пересечении линии связи A'A" с осью х отметим вспомогательную точку А_х (рис. 9).

2. Проведем линию связи из горизонтальной проекции точки А' у_π1, отметим вспомогательную точку А_у.

3. Перенесем вспомогательную точку А_у на ось у_π3. Для этого поставим циркуль в начало координат (точка О) радиусом ОАу и проведем дугу до оси у_π3.

4. Из фронтальной проекции точки A" проведем линию связи z и на оси z отметим вспомогательную точку А_z.

5. На пересечении линий связи, проведенных из точки А_у и А_z перпендикулярно осям у и z, определим профильную проекцию точки А'''.

6. Для нахождения профильной проекции В''' проведем линии связи х и z, отметим на оси х вспомогательную точку В_х, на оси z‑ точку В_z. В_у находится в начале координат, т.к. координата у для точки В равна 0. Помня о том, что В''В''' z, отметим на оси z В''', совпадающую с В_z.

7. Для построения недостающей проекции С''' рассуждаем следующим образом: С'(10, 0); С''(10, 0), где z=0 и у=0, следовательно, С'''(у, z) =>С'''(0, 0) находится в начале координат, в точке О.

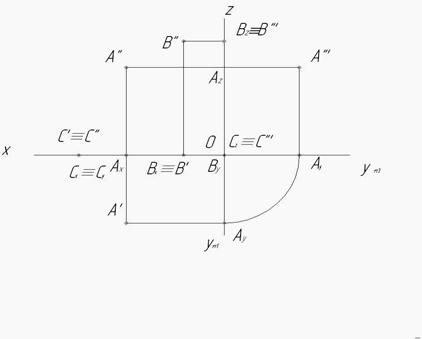
Рис.9

Построим наглядные изображения точек А, В, С (рис.10).

Изображаем три взаимно перпендикулярные плоскости π₁, π₂, π₃.

Ось у направляем под углом 45º к оси х. При построении наглядного изображения принимаем коэффициент искажения по осям к_х=к_z=1, к_y=0,5.

1. Отметим вспомогательные точки А_х, А_у, А_z, измеряя расстояния на эпюре Монжа.

2. Строим проекции А', А'', А'''.

А'=(Ах А'׀׀у)∩( Ау А'х׀׀)

А''=(Ах А''׀׀z)∩(А''' Аz׀׀х)

А'''=( Ау А'''׀׀z)∩( Аz А'''׀׀у)

3. Строим наглядное изображение точки А.

Проведем (А' А) ׀׀z

(А'' А) ׀׀ у (А''' А) ׀ ׀x, на пересечении этих линий получим точку А.

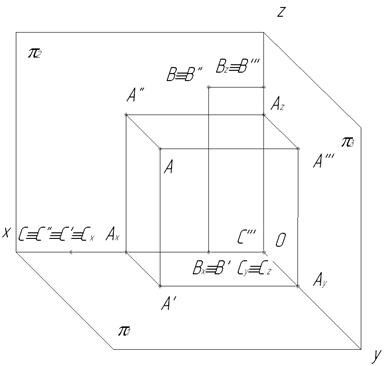
Рис. 10

Если точка лежит в пространстве, то на эпюре ни одна из ее проекций с самой точкой не совпадает. Если одна из координат равна нулю - точка лежит на плоскости и совпадает со своей проекцией на этой плоскости, при равенстве нулю двух координат - точка лежит на оси. При равенстве всех трех координат 0 – точка лежит в начале координат.

π₁ – горизонтальная плоскость проекций

π₂ – фронтальная плоскость проекций

π₃ – профильная плоскость проекций

Из (•) А опускаем _┴ на 3 плоскости и получаем проекции точки на этих плоскостях:

А' - горизонтальная проекция (•) А

А" - фронтальная проекция (•) А

A"' - профильная проекция (•) А

При построении (•) на эпюре горизонтальная проекция А' характеризуется координатами х, у;

фронтальная А" – х, z;

профильная A"' - у, z.

Рис.8

1. На пересечении линии связи A'A" с осью х отметим вспомогательную точку А_х (рис. 9).

2. Проведем линию связи из горизонтальной проекции точки А' у_π1, отметим вспомогательную точку А_у.

4. Из фронтальной проекции точки A" проведем линию связи z и на оси z отметим вспомогательную точку А_z.

Рис.9

Построим наглядные изображения точек А, В, С (рис.10).

Изображаем три взаимно перпендикулярные плоскости π₁, π₂, π₃.

1. Отметим вспомогательные точки А_х, А_у, А_z, измеряя расстояния на эпюре Монжа.

2. Строим проекции А', А'', А'''.

А'=(Ах А'׀׀у)∩( Ау А'х׀׀)

А''=(Ах А''׀׀z)∩(А''' Аz׀׀х)

А'''=( Ау А'''׀׀z)∩( Аz А'''׀׀у)

3. Строим наглядное изображение точки А.

Проведем (А' А) ׀׀z

(А'' А) ׀׀ у (А''' А) ׀ ׀x, на пересечении этих линий получим точку А.

Рис. 10

2) Каким это образом по трем искаженным (в общем случае) проекциям геометрической фигуры (а тень очень редко соответствует своему оригиналу) можно определить его конфигурацию и положение в пространстве?

3) Почему, проецируя предмет на три взаимно перпендикулярные плоскости проекций, которые пересекаются по осям x, y, z, в начертательной геометрии чаще пользуются безосными чертежами?

4) В начертательной геометрии утверждается, что предмет проецируется, в общем случае, на плоскости проекций с искажением. Тогда почему "искаженные проекции" облегчает процесс выполнения и чтения чертежа?

Ответить на эти вопросы Вы сможете, изучив курс Начертательной геометрии.

Читайте также: