Что такое геометрическое место точек кратко

Обновлено: 08.07.2024

Пожалуй, самым первым приходящим на ум геометрическим местом точек (ГМТ) является окружность . Каждая точка окружности удалена от некоторой точки, называемой центром на расстояние R . Вспомните, какие действия мы производим при попытке начертить ровную окружность. Разводим ножки циркуля на выбранное расстояние , обязательно при этом фиксируем это расстояния, насколько позволяет инструмент. Это важный пункт, ибо если в процессе изображения окружности собьётся расстояние, то никакой окружности не получится. Далее, устанавливаем иглу в выбранный центр и оставляем грифелем след во всех местах, где это возможно.

Казалось бы, какие очевидные вещи сейчас обсуждаются, но не это ли свойство ГМТ используется, например, при поиске пропавших туристов или даже воздушных судов? Если со времени последнего известного положения интересующего объекта X прошло время t , то при максимальной скорости объекта V он мог преодолеть расстояние R=Vt . Важно что, после потери контакта с объектом направление его движения может быть самым непредсказуемым. Именно поэтому говорят о зоне поиска в окружности, радиусом R .

ГМТ на практике

Вспомним трагические события 2014 года, когда бесследно исчез пассажирский самолет рейса 370. До сих пор кроме предположений нет никакой информации о судьбе всех его пассажиров. Сейчас нас будет интересовать то, каким образом поисковый штаб ограничил часть земной поверхности, в которой предположительно мог находиться потерянный самолет.

Поскольку известна последняя точка, где самолет был зафиксирован радиолокатором и после этого не выходил на связь, то в самом пессимистичном случае он не мог преодолеть расстояние, более чем ему бы позволил остаток топлива. А так как дальнейший маршрут полета неизвестен, то, опять же, в самом пессимистичном случае необходимо применить это самое свойство ГМТ.

Количество этих самых ГМТ довольно внушительно и можно только представить сколько полезной работы человек доверил этим математическим понятиям.

Если рассматривать вышеуказанную задачу не на плоскости, а трехмерном пространстве, то получим сферу. Более строгое определение этого – ГМТ равноудаленных от одной точки в пространстве, есть сфера с центром в данной точке . Это математическое свойство несомненно учитывается при определении координат в спутниковых системах навигации. Поскольку спутники находятся довольно далеко от поверхности планеты, то принимается модель сферического распространения радиоволн от точечного источника.

Более сложный случай ГМТ

Это всего пара примеров, где выполняющееся для точек условием было предельно простым. Это всего лишь равенство. Конкретно равенство расстояний. Но что будет, если в качестве условия будет поставлено более сложное выражение. Тут как из рога изобилия будут высыпаться еще более интересные случаи.

Что мы видим на рисунке выше? Да это всем известная гипербола . Вот же ее фокусы в точках (-с,0) и (с,0). А знаете ли вы, что это не менее удивительное ГМТ? Для всех точек гиперболы верно условие d2 – d1 = 2a. Простыми словами – разность между расстояниями от фокусов до любой точки гиперболы постоянна. “И что?” – это самый желанный вопрос, потому что на этом принципе работают другие системы навигации, важность которых в деятельности человека недооценить невозможно. Их еще называют системами гиперболического типа и красота математики этих решении просто запредельная . Об этом вы лучше узнаете из этой статьи.

А какие геометрические места точек и области их применения знаете вы?

Канал, которому посвящено мое сегодняшнее промо - канал моего друга - специалиста, обладающего широчайшим спектром знаний об IT-технологиях. На своем ДЗЕН-канале , а также на YouTube он простым языком объясняет не только многие моменты из мира компьютеров и электроники, но и ставит настоящие эксперименты!

Геометри́ческое ме́сто то́чек (ГМТ) — так в математике называют геометрическую фигуру, которая является множеством точек, обладающих некоторым свойством.
Вообще говоря, любая геометрическа фигура является множеством точек, но лишь некоторые являются ГМТ.
Примеры:
Серединный перпендикуляр к отрезку есть геометрическое место точек, равноудалённых от концов отрезка.
Окружность есть геометрическое место точек, равноудалённых от данной точки, называемой центром окружности.
Парабола есть геометрическое место точек, равноудалённых от точки (называемой фокусом) и прямой (называемой директрисой)
Биссектриса есть геометрическое место точек, равноудаленных от сторон угла

ТЕМА УРОКА: Геометрическое место точек.

Содержание

Цели урока:

Образовательная: показать новый метод решения задач на построение геометрического места точек; Научить применять его в решении задач.
Развивающая: развитие наглядно- образного мышления; познавательного интереса.
Воспитывающая: развитие умения планировать работу, искать рациональные пути ее выполнения, способности аргументировано отстаивать свое мнение, критически оценивать результат.

Задачи урока:

Изучения нового материала.
Проверить умение учащихся решать задачи.

План урока:

Определения.
Пример 1.
Пример 2.
Пример 3.
Теоретическая часть.
Общии понятия.

Введение.

Древнеегипетскую и вавилонскую культуру в области математики продолжали греки. Они не только усвоили весь опыт их геометрии, но и пошли гораздо дальше. Ученые древней Греции сумели привести в систему накопленные геометрические знания и, таким образом, заложить начала геометрии как дедуктивной науки.

Греческие купцы познакомились с восточной математикой, прокладывая торговые пути. Но люди Востока почти не занимались теорией, и греки быстро это обнаружили. Они задавались вопросами: почему в равнобедренном треугольнике два угла при основании равны; почему площадь треугольника равна половине площади прямоугольника при одинаковых основаниях и высотах?

К сожалению, не сохранилось первоисточников, описывающих ранний период развития греческой математики. Только благодаря восстановленным текстам четвертого столетия до нашей эры и трудам арабских ученых, которые были богаты переводами сочинений авторов античной Греции, мы располагаем изданиями Евклида, Архимеда, Аполлония и других великий людей. Но в этих произведениях уже представлена вполне развитая математическая наука.

Математика древней Греции прошла длительный и сложный путь развития, начиная с VI столетия до н.э. и по VI век. Историки науки выделяют три периода ее развития в соответствии с характером знаний:

Накопление отдельных математических фактов и проблем (6 - 5B.B. до н.э.).
Систематизация полученных знаний (4 - 3 в.в. до н.э.).
Период вычислительной математики (3в. до н.э. - 6 в.).

Геометрическое место точек (ГМТ).

Определения.

Геометрическое место – термин, применявшийся в старой литературе по геометрии и до сих пор применяющийся в учебной литературе, для обозначения множества точек, удовлетворяющих некоторому условию, как правило, геометрического характера. Например: геометрическое место точек, равноудаленных от двух данных точек A и B – это серединный перпендикуляр к отрезку AB. Иногда говорят и о геометрическом месте прямых и других фигур.

Геометрическое Место Точек (ГМТ) - в геометрии траектория некоторой точки, перемещающейся в соответствии с данной формулой или условием. Например, круг является геометрическим местом точки, перемещающейся на плоскости так, что расстояние от места ее нахождения до центра остается неизменным.

Геометрическое место точек (ГМТ) - это множество точек, в которое попадают все точки, удовлетворяющие определенному условию, и только они.

Геометрическое место точек (ГМТ) - фигура речи в математике, употребляемая для определения геометрической фигуры как множества точек, обладающих некоторым свойством.

Примеры.

Серединный перпендикуляр к отрезку есть геометрическое место точек, равноудалённых от концов отрезка.
Окружность есть геометрическое место точек, равноудалённых от данной точки, называемой центром окружности.
Парабола есть геометрическое место точек, равноудалённых от точки (называемой фокусом) и прямой (называемой директрисой).

Пример 1.

Срединный перпендикуляр любого отрезка есть геометрическое место точек (т.е. множество всех точек), равноудалённых от концов этого отрезка. Пусть PO перпендикулярно AB и AO = OB :

Тогда, расстояния от любой точки P, лежащей на срединном перпендикуляре PO, до концов A и B отрезка AB одинаковы и равны d .

Таким образом, каждая точка срединного перпендикуляра отрезка обладает следующим свойством: она равноудалена от концов отрезка.

Пример 2.

Биссектриса угла есть геометрическое место точек, равноудалённых от его сторон.

Пример 3.

Окружность есть геометрическое место точек (т.е. множество всех точек), равноудалённых от её центра ( на рис. показана одна из этих точек – А ).

Окружность

Теоретическая часть.

Окружность - это геометрическое место точек (т.е. множество всех точек) на плоскости, равноудалённых от одной точки, называемой центром окружности. Отрезок, соединяющий центр окружности с какой-либо её точкой, называется радиусом и обозначается r или R. Часть плоскости, ограниченная окружностью, называется кругом. Часть окружности ( AmB, рис.1 ) называется дугой. Прямая PQ, проходящая через точки M и N окружности ( рис.1 ), называется секущей, а её отрезок MN, лежащий внутри окружности - хордой.

Хорда, проходящая через центр круга ( например, BC, рис 1), называется диаметром и обозначается d или D . Диаметр – это наибольшая хорда, равная двум радиусам (d = 2 r).

Касательная. Предположим, секущая PQ ( рис.2 ) проходит через точки K и M окружности. Предположим также, что точка M движется вдоль окружности, приближаясь к точке K. Тогда секущая PQ будет менять своё положение, вращаясь вокруг точки K. По мере приближения точки M к точке K секущая PQ будет стремиться к некоторому предельному положению АВ. Прямая AB называется касательной к окружности в точке K. Точка K называется точкой касания. Касательная и окружность имеют только одну общую точку – точку касания.

Свойства касательной.

Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания ( AB перпендикулярно OK, рис.2 ).
Из точки, лежащей вне круга, можно провести две касательные к одной и той же окружности; их отрезки равны АВ=АС ( рис.3 ).

Сегмент – это часть круга, ограниченная дугой ACB и соответствующей хордой AB ( рис.4 ). Длина перпендикуляра CD, проведенного из середины хорды AB до пересечения с дугой ACB, называется высотой сегмента.

рис. 4
Сектор – это часть круга, ограниченная дугой AmB и двумя радиусами OA и OB, проведенными к концам этой дуги ( рис.5 ).

Углы в круге.

Центральный угол – угол, образованный двумя радиусами ( ∠AOB, рис.5 ). Вписанный угол – угол, образованный двумя хордами AB и AC, проведенными из их одной общей точки ( ∠BAC, рис.4 ). Описанный угол – угол, образованный двумя касательными AB и AC, проведенными из одной общей точки ( ∠BAC, рис.3 ).

Соотношения между элементами круга.

Вписанный угол ( ∠ABC, рис.7 ) равен половине центрального угла, опирающегося на ту же дугу AmC ( ∠AOC, рис.7 ). Поэтому, все вписанные углы ( рис.7 ), опирающиеся на одну и ту же дугу ( AmC, рис.7 ), равны. А так как центральный угол содержит то же количество градусов, что и его дуга ( AmC, рис.7 ), то любой вписанный угол измеряется половиной дуги, на которую он опирается ( в нашем случае AmC ).

Все вписанные углы, опирающиеся на полукруг (∠APB, ∠AQB, …, рис.8 ), прямые.

Угол (∠AOD, рис.9 ), образованный двумя хордами ( AB и CD ), измеряется полусуммой дуг, заключённых между его сторонами: ( AnD + CmB ) / 2 .

Угол (∠AOD, рис.10), образованный двумя секущими ( AO и OD ), измеряется полуразностью дуг, заключённых между его сторонами: ( AnD – BmC ) / 2.

Угол (∠DCB, рис.11), образованный касательной и хордой ( AB и CD ), измеряется половиной дуги, заключённой внутри него: CmD / 2.

Угол (∠BOC, рис.12), образованный касательной и секущей ( CO и BO ), измеряется полуразностью дуг, заключённых между его сторонами: ( BmC – CnD ) / 2 .

Описанный угол (∠AOC, рис.12), образованный двумя касательными ( CO и AO ), измеряется полуразностью дуг, заключенных между его сторонами: ( ABC – CDA ) / 2 .

Произведения отрезков хорд ( AB и CD, рис.13 или рис.14), на которые они делятся точкой пересечения, равны: AO · BO = CO · DO.

Квадрат касательной равен произведению секущей на её внешнюю часть ( рис.12): OA 2 = OB · OD. Это свойство можно рассматривать как частный случай рис.14.

Хорда ( AB , рис.15), перпендикулярная диаметру ( CD ), O пополам: AO = OB .

Интересный факт:

Поздравляем с Пи-раздником вас.

Выражаясь научным языком, число "Пи" - это отношение длины окружности к ее диаметру. Простая вроде бы вещь, но волнует умы математиков с глубокой древности. И продолжает волновать. До такой степени, что ученые - лет 20 назад - договорились отмечать праздник этого числа. И призвали присоединиться к торжествам всю прогрессивную общественность. Она присоединяется: ест круглые Пи-роги, вы-ПИ-вает, обязательно Пи-во и издает звуки Пи при встрече.

Фанаты будут соревноваться, вспоминая знаки числа "Пи". И постараются превзойти рекорд 24-летнего китайского студента Лю Чао, который назвал по памяти без ошибок 68890 знаков. На это у него ушло 24 часа и 4 минуты.

Отправление торжеств назначено на 14 марта - дату, которая в американском написании выглядит как 3.14 - то есть, первыми тремя цифрами числа "Пи".
По легенде, о числе "Пи" знали еще вавилонские жрецы. Использовали при строительстве Вавилонской башни. Но не смогли точно вычислить его значение и от этого не справились с проектом. Сам символ числа "Пи" впервые использовал в своих трудах в 1706 году математик Уильям Джон (William Jones). Но реально он прижился после 1737 года благодаря стараниям шведского математика Леонарда Эйлера (Leonhard Euler).

Отмечать праздник придумал американский физик Ларри Шо (Larry Shaw).
На вопрос, сколько знаков в числе "Пи" после запятой, точного ответа нет. Скорее всего, их бесконечное число. А главная особенность в том, что последовательность этих знаков не повторяется. Сегодня их известно 12411 триллионов. Обследовано 500 миллиардов. И повторений не найдено.

Как считают некоторые видные физики и математики, например Дэвид Бейли, Питер Борвин и Саймон Плофе (David Bailey, Peter Borewin, Simon Plouffe), их - повторений - не найти никому и никогда. Хоть испиши знаками всю Вселенную. Да хоть сколько Вселенных. И в этом ученые видят некую скрытую мистику. Полагают, что в числе "Пи" зашифрован бесконечный первородный хаос, ставший потом гармонией. Или какая-то загадочная информация.

Сформулируйте определение окружности и круга?
С какими новыми понятиями вы познакомились?
Что называется геометрическим местом точек?
Какая разница между диаметром и радиусом?
Как найти радиус окружности какая описана около треугольника?

Список использованных источников:

Над уроком работали:

Поставить вопрос о современном образовании, выразить идею или решить назревшую проблему Вы можете на Образовательном форуме, где на международном уровне собирается образовательный совет свежей мысли и действия. Создав блог, Вы не только повысите свой статус, как компетентного преподавателя, а и сделаете весомый вклад в развитие школы будущего. Гильдия Лидеров Образования открывает двери для специалистов высшего ранга и приглашает к сотрудничеству в направлении создания лучших в мире школ.

Геометрическим местом точек (в дальнейшем ГМТ), называется фигура плоскости, состоящая из точек обладающих некоторым свойством, и не содержащая ни одной точки, не обладающей этим свойством.

Мы будем рассматривать только те ГМТ, которые можно построить с помощью циркуля и линейки.

Рассмотрим ГМТ на плоскости, обладающие простейшими и наиболее часто выражающимися свойствами:

1) ГМТ, отстоящих на данном расстоянии r от данной точки О, есть окружность с центром в точке О радиуса r.

2) ГМТ равноудаленных от двух данных точек А и В, есть прямая, перпендикулярная к отрезку АВ и проходящая через его середину.

3) ГМТ равноудаленных от двух данных пересекающихся прямых, есть пара взаимно перпендикулярных прямых, проходящих через точку пересечения и делящих углы между данными прямыми пополам.

4) ГМТ, отстоящих на одинаковом расстоянии h от прямой, есть две прямые, параллельные этой прямой и находящиеся по разные стороны от нее на данном расстоянии h.

5) Геометрическое место центров окружностей, касающихся данной прямой m в данной на ней точке М, есть перпендикуляр к АВ в точке М (кроме точки М).

6) Геометрическое место центров окружностей, касающихся данной окружности в данной на ней очке М, есть прямая, проходящая через точку М и центр данной окружности (кроме точек М и О).

7) ГМТ, из которых данный отрезок виден под данным углом, составляет две дуги окружностей, описанных на данном отрезке и вмещающих данный угол.

8) ГМТ, расстояния от которых до двух данных точек А и В находятся в отношении m : n, есть окружность (называемая окружностью Аполлония).

9) Геометрическое место середин хорд, проведенных из одной точки окружности, есть окружность, построенная на отрезке, соединяющем данную точку с центром данной окружности, как на диаметре.

10) Геометрическое место вершин треугольников равновеликих данному и имеющих общее основание, составляет две прямые, параллельные основанию и проходящие через вершину данного треугольника и ему симметричного относительно прямой, содержащей основание.

Приведем примеры отыскания ГМТ.

ПРИМЕР 2. Найти ГМТ, являющихся серединами хорд, проведенных из одной точки данной окружности (ГМТ № 9).

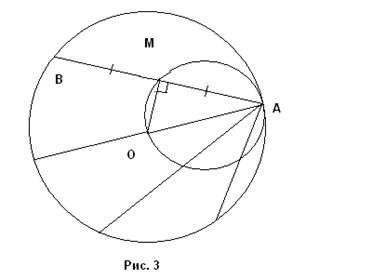
Решение . Пусть дана окружность с центром О и на этой окружности выбрана точка А из которой проводятся хорды. Покажем, что искомое ГМТ есть окружность, построенная на АО как на диаметре (кроме точки А) (рис. 3).

Пусть АВ - некоторая хорда и М – ее середина. Соединим М и О. Тогда МО ^ АВ (радиус, делящий хорду пополам, перпендикулярен этой хорде). Но, тогда ÐАМО = 90 0 . Значит М принадлежит окружности с диаметром АО (ГМТ № 7). Т.к. эта окружность проходит через точку О, то О принадлежит нашему ГМТ.

Обратно, пусть М принадлежит нашему ГМТ. Тогда, проведя через М хорду АВ и соединив М и О, получим, что ÐАМО = 90 0 , т.е. МО ^ АВ, а, значит, М – середина хорды АВ. Если же М совпадает с О, то О - середина АС.

Часто метод координат позволяет находить ГМТ.

ПРИМЕР 3. Найти ГМТ, расстояние от которых до двух данных точек А и В находятся в данном отношении m : n (m ≠ n).

Решение . Выберем прямоугольную систему координат так, чтобы точки А и В располагались на оси Ох симметрично относительно начала координат, а ось Оу проходила через середину АВ (рис.4). Положим АВ = 2a. Тогда точка А имеет координаты А (a, 0), точка В - координаты В (-a, 0). Пусть С принадлежит нашему ГМТ, координаты С(х, у) и CB/CA = m/n. Но Значит

Преобразуем наше равенство. Имеем

После раскрытия скобок и приведения подобных слагаемых, получаем

Разделим левую и правую части последнего неравенства на (это можно сделать, так как по условию ), затем выделим полный квадрат относительно х. Получаем

Но последнее уравнение задает окружность с центром в точке и радиусом Таким образом, если точка удовлетворяет условиям задачи, то она принадлежит (**).

Обратно, пусть координаты точки С(x,y) удовлетворяют уравнению (**). Проделывая все выкладки в обратную сторону, приходим к равенству (*), что и доказывает принадлежность точки С нашему ГМТ.

Определение.