Сообщение задача о кенигсбергских мостах

Обновлено: 05.07.2024

Проблема семи мостов Кёнигсберга или Задача о кёнигсбергских мостах (нем. Königsberger Brückenproblem ) — старинная математическая задача, в которой спрашивалось, как можно пройти по всем семи мостам Кёнигсберга, не проходя ни по одному из них дважды. Впервые была решена в 1736 году немецким и русским математиком Леонардом Эйлером.

Содержание

История

Издавна среди жителей Кёнигсберга была распространена такая загадка: как пройти по всем мостам (через реку Преголя), не проходя ни по одному из них дважды. Многие кёнигсбержцы пытались решить эту задачу как теоретически, так и практически, во время прогулок. Впрочем, доказать или опровергнуть возможность существования такого маршрута никто не мог.

Решение задачи по Леонарду Эйлеру

На упрощённой схеме части города (графе) мостам соответствуют линии (дуги графа), а частям города — точки соединения линий (вершины графа). В ходе рассуждений Эйлер пришёл к следующим выводам:

Число нечётных вершин (вершин, к которым ведёт нечётное число рёбер) графа должно быть чётно. Не может существовать граф, который имел бы нечётное число нечётных вершин.
Если все вершины графа чётные, то можно, не отрывая карандаша от бумаги, начертить граф, при этом можно начинать с любой вершины графа и завершить его в той же вершине.
Граф с более чем двумя нечётными вершинами невозможно начертить одним росчерком.

Граф кёнигсбергских мостов имел четыре (синим) нечётные вершины (то есть все), следовательно, невозможно пройти по всем мостам, не проходя ни по одному из них дважды.

Упрощённая схема мостов Кёнигсберга. Значение букв и цифр — см. комментарий к старинной карте Кёнигсберга

Созданная Эйлером теория графов нашла очень широкое применение в транспортных и коммуникационных системах (например, для изучения самих систем, составления оптимальных маршрутов доставки грузов или маршрутизации данных в Интернете).

Нетрадиционные решения задачи

Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена.
Вы можете отредактировать эту статью, добавив ссылки на авторитетные источники.
Эта отметка установлена 12 мая 2011.

На карте старого Кёнигсберга был ещё один мост, появившийся чуть позже и соединявший остров Ломзе с южной стороной. Своим появлением этот мост обязан самой задаче Эйлера-Канта. Произошло это при следующих обстоятельствах.

Леонард Эйлер. Задача о кенигсбергских мостах

Решение задачи о кенигсбергских мостах, точнее предложенный при этом метод, лежит в основе теории графов. А изложение этого решения можно найти в нескольких письмах Эйлера его коллегам. Например, в письме Карлу Готлибу Элеру от 3 апреля 1736 года. Ниже следует фрагмент этого письма, перепечатанный из книги: Леонард Эйлер. Письма к ученым, М.-Л., 1963.

Наконец, ты, славнейший муж, выражаешь желание ознакомиться с моим способом построения мостов; охотно представляю этот способ на твой суд. Ибо, когда ты попросил у меня решения этой проблемы, приспособленной к частному случаю Кёнигсберга, ты, вероятно, считал, что я предложил такого рода построение мостов, но я не сделал это, а только доказал, что такое построение вообще не может иметь места, и это следует принять вместо решения. Способ же мой является универсальным, так как с его помощью в любом предложенном мне случае этого рода я тотчас могу решить, следует ли строить переход с помощью отдельных мостов или нет, и в первом случае [могу установить], каким образом этот переход следует осуществить. Далее я изложу мой способ, а также опишу путь, которым я к нему пришел.

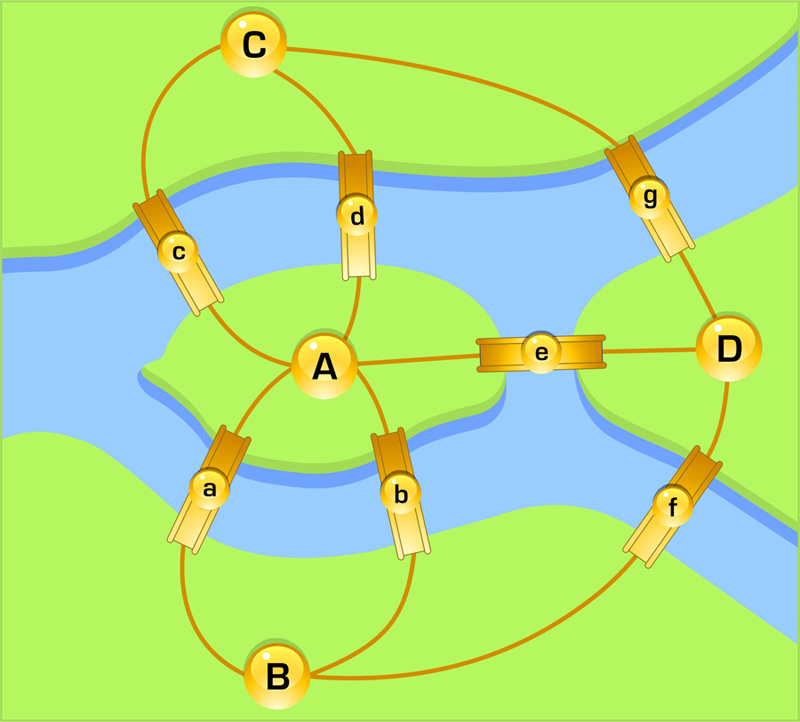
Я рассмотрел произвольно взятую фигуру разветвления реки, а также мосты а, b, с, d, e, f, как это указано на рис. 1, и установил, что возможен переход, который я представляю следующим образом. Области, отделенные друг от друга водой, я называю буквами А, В, С, и когда предполагается переход через мосты из одной области в другую, [а именно] переход из А в В через мост или а или b, — наиболее удобно назвать [буквами] АВ, из которых первая буква А будет обозначать область, из которой переходят.

Итак, АВСАСАВ будет определять переход, совершаемый через все мосты по одному разу; число этих букв должно быть на единицу больше, чем число мостов; это должно иметь место при любом возможном переходе описанным способом, в чем каждому легче убедиться самому, чем доказывать. Теперь я рассматриваю, сколько раз в ряде букв А, В, С, А, С, А, В должны встретиться буквы ABC, о чем нужно судить по числу мостов, ведущих в каждую из областей. Так, к области А ведут пять мостов: а, b, с, d, e, и сколько раз буква А встречается в середине того ряда, столько раз встречаются два из этих мостов, ибо с одной стороны нужно перейти в область А, с другой стороны — выйти оттуда. Если А встречается или в начале, или в конце того ряда, тогда единственный переход моста соответствует А. Отсюда следует, что, если число мостов, ведущих в область А, будет нечетным, тогда переход через все мосты не может совершиться иначе, чем таким образом, чтобы он или начинался в области А, или заканчивался в области А. А если число мостов, ведущих к А, будет четным, тогда переход может быть совершен и без этого условия, чтобы начинаться или заканчиваться в А, но если он начинается в А, то должен будет там же и закончиться. Отсюда вытекает, что в ряде АВСАСАВ любая буква, за исключением первой и последней, обозначает переход, ведущий через два моста в область, обозначенную этой буквой.

Следовательно, надо держаться следующего правила: если на каком-либо рисунке число мостов, ведущих в некоторую область, будет нечетным, тогда желаемый переход через все мосты одновременно не может быть осуществлен иначе, как если переход или начинается, или заканчивается в этой области. А если число мостов четное, отсюда не может возникнуть никакого затруднения, так как ни начало, ни конец перехода при этом не фиксируются. Отсюда следует такое общее правило: если будет больше чем две области, к которым ведет нечетное количество мостов, тогда желательный переход вообще не может быть совершен. Ибо представляется совершенно невозможным, чтобы переход и начинался, и заканчивался в какой-нибудь одной из этих областей. А если будут только две области такого рода (так как не могут быть даны одна область этого рода или нечетное число областей), тогда может быть совершен переход через все мосты, но с таким условием, чтобы начало перехода было в одной, а конец в другой из этих областей. Когда в предложенной фигуре А и В есть области, к которым ведет нечетное число мостов, а число мостов, ведущих к С, является четным, то я считаю, что переход или построение мостов может иметь место, если переход начинается или из А, или из В, а если же кто-нибудь пожелает начать переход из С, то он никогда не сможет достигнуть цели. В расположении кенигсбергских мостов я имею четыре области А, В, С, D, взаимно отделенные друг от друга водой, к каждой из которых ведет нечетное число мостов (рис. 2).

Таким образом, поскольку есть больше чем две области, к которым ведет нечетное число мостов, я утверждаю, что я доказал полную невозможность такого соединения мостов. Итак, с помощью очень легкого правила можно почти мгновенно определить для любой фигуры, допускается ли такого рода построение мостов, при котором переход будет происходить только через все мосты одновременно, или нет? Ибо возможным будет построение, если и не будет никакой области, или будут только две, к которым ведет нечетное число мостов; в таких случаях начало перехода выбирается произвольно, но там же должен быть и конец перехода. В последнем же случае начало перехода должно иметь место в одной из тех областей, а конец — в другой. Построение невозможно, если будет более чем две области, к которым поведет нечетное число мостов.

Следовательно, ты можешь убедиться, славнейший муж, что это решение по своему характеру, по-видимому, имеет мало отношения к математике, и мне непонятно, почему следует скорее от математика ожидать этого решения, нежели от какого-нибудь другого человека, ибо это решение подкрепляется одним только рассуждением и нет необходимости привлекать для нахождения этого решения какие-либо законы, свойственные математике. Итак, я не знаю, каким образом получается, что вопросы, имеющие совсем мало отношения к математике, скорее разрешаются математиками, чем другими [учеными]. Между тем ты, славнейший муж, определяешь место этого вопроса в геометрии положения, и что касается этой новой науки, то, признаюсь, мне неизвестно, какого рода относящиеся сюда задачи желательны были Лейбницу и Вольфу. Итак, я прошу тебя, если ты считаешь, что я способен нечто создать в этой новой науке, чтобы ты соблаговолил мне прислать несколько определенных, относящихся к ней задач.

Vego 10.04.2006 21:19 Ответить

Чесно говоря, абсолютно непонятно, чем предложеный подход отличается, например, от UNL или просто блок-схем в программировании. Тоесть эти принципы появились вместе со структурным программированием и получили развитие в объектно-ориентированых языках.
Правда, другое дело, что не всем абстрактное мышление привычно.

Lev Vego 24.04.2006 14:04 Ответить

kak 19.04.2006 21:34 Ответить

". Модулем называется объект реального мира, который его наблюдатель счел целесообразным представить в виде образующей и использовать ее в качестве модели этого объекта."
Кто-нибудь может ответить, чем объект отличается от модуля? Зачем вводится еще одна сущность? Если есть объект и есть модель объекта.

Lev kak 29.04.2006 12:18 Ответить

kak Lev 03.05.2006 09:35 Ответить

Для Lev:
Я попробовал разобраться с приведенной Вами терминологией (толковый словарь), но, к сожалению, наткнулся на ряд трудностей в части терминов:
- данные это информация;
- информация это сведения или знания;
- сведения это события;
- событие это одномоментное идентифицируемое изменение состояния некоторой системы;
- знания, система, изменение, модуль - не определены;
- идентификация это присвоение субъектам или объектам доступа идентификатора и (или) сравнение предъявляемого идентификатора с перечнем присвоенных идентификаторов;
- объект это общий термин, которым обозначается любая индивидуально выделяемая сущность. Предмет или явление, которому можно присвоить название
Из этого набора получается, что данные = информация = сведения = события, при этом не указано, кто идентифицирует и в какой системе происходит изменения, в идентифицируемой или идентифицирующей? Кроме того, цепочка обрывается, так как нет определения некоторых терминов (знания, система, изменение.)

mb kak 16.06.2006 00:19 Ответить

Уважаемый kak, это же не теория, а (прошу прощения у автора, но истина дороже) полная туфта. То есть наоборот, пустая.

alexlotov 03.01.2008 11:36 Ответить

"теория модулей" - Новая парадигма Нового мировоззрения Нового тысячелетия - Древняя Философия Вечных Цивилизаций - ДФ ВЦ. (Гуглим)

"модульные сети" - вечная и бесконечная Паутина из так называемых вечных цивилизаций, которые могут породить и отремонтировать эту Паутину. Развитие цивилизации есть развитие феномена сознания. Предел развития всех цивилизаций есть Осознающий Бог.

zodiac_z 08.09.2011 23:27 Ответить

Известно, что великий швейцарский математик Эйлер создал целое направление науки, решая задачу о семи кенигсбергских мостах. Существует легенда, что жители Кенигсберга любили прогуливаться по улицам трех "слившихся" в единое целое средневековых городов: Альштадта, Лебенихта и Кнайпхофа - но терпеть не могли зря топтать свои башмаки. А города эти были соединены между собой семью мостами. И вот будто бы экономные горожане однажды задумались: а можно ли пройти по всем мостам так, чтобы на каждом из них побывать лишь один раз и вернуться к месту, откуда начал прогулку?

Эйлера задача заинтересовала. "Никто еще до сих пор не смог это проделать, но никто и не доказал, что это невозможно. Для решения недостаточны ни геометрия, ни алгебра, ни комбинаторское искусство", - так писал он своему коллеге, итальянскому математику и инженеру.

В конце концов, выстроив сложнейший алгоритм, Эйлер получил отрицательный ответ. Пройти по всем мостам лишь по одному разу и, описав круг, вернуться в исходную точку, оказалось невозможным.

Число нечётных вершин (вершин, к которым ведёт нечётное число рёбер) графа должно быть чётно. Не может существовать граф, который имел бы нечётное число нечётных вершин.

Если все вершины графа чётные, то можно, не отрывая карандаша от бумаги, начертить граф, при этом можно начинать с любой вершины графа и завершить его в той же вершине.

Граф с более чем двумя нечётными вершинами невозможно начертить одним росчерком .

Граф кёнигсбергских мостов имел четыре нечётные вершины (то есть все), следовательно, невозможно пройти по всем мостам, не проходя ни по одному из них дважды.

Созданная Эйлером теория графов нашла очень широкое применение: например, её используют при изучении транспортных и коммуникационных систем, в частности, для маршрутизации данных в Интернете.

Любопытно, что другое решение задачи предложил кайзер Вильгельм. На приёме ему поднесли карту Кёнигсберга и предложили решить загадку семи мостов. Вильгельм не растерялся, а тут же приказал построить восьмой мост. После чего задача стала легкорешаемой.

Третье решение придумали речники. За небольшую плату они предлагают перевезти всех, кому не хватает моста для решения задачки.

Кенигсберг был построен на берегу реки Прегель (Преголя), которая разделила город на четыре отдельных жилых массива. Люди перебирались из одного района в другой через семь различных мостов. Согласно легенде, популярным развлечением во время воскресных прогулок были попытки пройти через весь город так, чтобы пересечь каждый мост только один раз. Никто так и не придумал, как это сделать, но это вовсе не значит, что задача не имеет решения.

Им просто нужно было обратиться к подходящему эксперту, чтобы узнать его.

В 1735 году мэр города Данцига (ныне польский Гданьск), расположенного в 120 километрах к западу от Кенигсберга, Карл Леонард Готлиб Эйлер, обратился к Леонарду Эйлеру с письмом, в котором просил о помощи в решении этой задачи от имени местного профессора математики по имени Генрих Кюн. Уже тогда Эйлер был знаменитым и весьма успешным математиком – он опубликовал свою первую книгу в течение года после этого письма, а за всю жизнь написал более 500 книг и статей.

Хотя у кого-то может возникнуть соблазн решить эту задачу, наметив все возможные маршруты через город, Эйлер сразу осознал, что эта стратегия потребует слишком много времени и не будет работать с другими схожими задачами (что, если в другом городе будет, скажем, двенадцать мостов?). Вместо этого он решил на время отвлечься от мостов и пометил участки суши буквами A, B, C и D. Таким образом, он теперь мог описать путешествие через мост из района А в район В как АВ, а путешествие из района А через район В район D как АВD. Здесь важно отметить, что количество букв в описании маршрута всегда будет на единицу больше, чем количество пересекаемых мостов. Так, маршрут АВ пересекает один мост, а маршрут АВD – два моста, и так далее. Эйлер понял, что поскольку в Кенигсберге семь мостов, а для того, чтобы пересечь их все, маршрут должен состоять из восьми букв, значит, решение задачи потребует именно восьми букв.

Затем он придумал более общее правило, используя еще более упрощенную схему. Если бы у вас было всего два сухопутных участка, А и В, и вы пересекали мост один раз, то участок А мог бы быть там, где путешествие начиналось, или там, где оно заканчивалось, но вы находились бы на участке А только однажды. Если бы вы пересекали мосты а, b и c по одному разу, то оказались бы на участке А ровно два раза. Это привело к созданию удобного правила: если у вас имеется четное число мостов, ведущих на один участок суши, вы должны добавить к этому числу единицу, а затем разделить полученную сумму на два, чтобы выяснить, сколько раз этот участок должен использоваться в ходе путешествия. (в данном примере, добавив единицу к количеству мостов, то есть к 3, получаем четыре, а разделив четыре на два получаем два, то есть именно дважды в путешествии пересекается участок А).

Этот результат вернул Эйлера к первоначальной проблеме. Есть пять мостов, которые ведут к участку А, поэтому в восьмибуквенном решении, которое он ищет, его придется пересекать три раза. У участков В, С и D есть по два моста, которые ведут к ним, поэтому каждый из них должен пересекаться дважды. Но 3+2+2+2 – это 9, а не 8, хотя по условию нужно пройти только через 8 участков и пересечь 7 мостов. Это означает, что невозможно пройти через весь город Кенигсберг, использовав каждый мост ровно один раз. Другими словами, в данном случае задача не имеет решения.

Однако, как и всякий истинный математик, Эйлер на этом не остановился. Он продолжал работать и создал более общее правило для других городов с другим количеством мостов. Если в городе нечетное количество мостов, то существует простой способ выяснить, можете ли вы совершить такое путешествие или нет: если сумма количества появлений каждой буквы, обозначающей участок земли, на единицу больше, чем количество мостов (как, например, в восьмибуквенном решении, о котором упоминалось ранее), такое путешествие возможно. Если же сумма больше этого числа, оно невозможно.

А как насчет четного количества мостов? В этом случае все зависит от того, с чего начать. Если вы начинаете с участка А и путешествуете по двум мостам, А в вашем решении появится дважды. Если вы начнете с другой стороны, то А появится только один раз. Если имеется четыре моста, тогда А появляется три раза, если этот участок был отправной точкой, или два раза, если не был. В общем виде это означает, что, если путешествие не начинается с участка А, он должен пересекаться вдвое меньшее количество раз, чем число мостов (четыре деленное на два дает два). Если же путешествие начинается с участка А, тогда он должен пересекаться на один раз больше.

Гениальность решения Эйлера заключается даже не в ответе, а в методе, который он применил. Это был один из первых случаев использования теории графов, также известной как теория сетей, весьма востребованной области математики в современном мире, заполненном транспортными, социальными и электронными сетями. Что касается Кенигсберга, в городе в конечном итоге появился еще один мост, который сделал решение Эйлера спорным, а затем британские войска разрушили большую часть города во время второй мировой войны. Сегодня и город и река имеют новые названия, но старинная задача живет в совершенно новой области математики.

Читайте также: