Сообщение отличие математические модели от натуральных

Обновлено: 05.07.2024

Модели можно классифицировать по-разному. Вариант группировки моделей, представляющий интерес для нашего исследования, приведен на рис. 3–1.

Материальные или абстрактные. Прежде всего можно выделить модели материальные и абстрактные.

Материальные модели наиболее доступны для понимания. Обычно это копии исследуемых предметов, часто — уменьшенные.

Статические материальные модели, например архитектурные, помогают наглядно представить размещение элементов на плоскости и пространственные соотношения. Примером динамических материальных моделей служит аэродинамическая труба, применяемая для изучения аэродинамических характеристик проектируемых летательных аппаратов.

Абстрактные модели состоят не из материальных элементов, а из символов, и применяются они гораздо чаще, чем материальные, но они не всегда считаются моделями. Используемая символика может иметь форму письменной речи или мыслительного процесса С помощью мысленного представления или словесного описания может быть построена модель фирмы и ее деятельности.

Хозяйственные руководители постоянно имеют дело с такими мысленными и словесными моделями фирмы. (Это мысленное представление о фирме, и оно не обязательно точное.)

Модели призваны заменить в нашем представлении реальную систему.

Математическая модель является особой разновидностью абстрактных моделей. Она выражается языком математических символов и, как другие абстрактные модели, является описанием представляемой системы. Математические модели широко применяются, но воспринимаются они труднее, чем материальные, и не столь часто встречаются в повседневной практике, как словесные модели.

Уравнения, описывающие напряжения в конструкции, представляют собой статическую математическую модель балок и опор. Уравнения движения планет вокруг солнца являются динамической математической моделью солнечной системы.

Математическая модель представляет собой более четкое описание, чем большинство словесных моделей. При построении математических моделей мы начинаем со словесных и уточняем их до тех пор, пока нам не удастся перевести их на язык математики. Сам по себе перевод не труден. При переходе от словесных утверждений к математическим трудности возникают в том случае, когда исходная словесная модель является неточным описанием и ее недостатки обнаруживаются при попытке преобразования в математическую форму.

Преимущество математической модели в сравнении со словесной или материальной заключается в том, что с ней легче оперировать, ее логическая структура более определенна, на ее основе легче проследить путь от предположений до вытекающих из них следствий.

Статические или динамические. Модели могут отражать ситуации, меняющиеся или не меняющиеся во времени. Статическая модель описывает взаимосвязи, не подверженные изменениям. В динамической модели рассматриваются отношения, изменяющиеся во времени.

Линейные или нелинейные. Системы, отображаемые в моделях, могут быть линейными и нелинейными; соответственно классифицируются и модели.

В линейной системе внешние воздействия просто суммируются[13]. При линейной трактовке предприятия удвоение числа поступающих заказов вызвало бы в любой последующий момент времени в десять раз большие изменения, чем увеличение объема заказов на 10 %. В такой модели предприятия не учитываются ограничения производственной мощности; производительность труда не должна снижаться даже в том случае, если возникнет избыток рабочей силы по сравнению с наличным оборудованием, а осуществление крупных изменений мощности предприятия требует не больше времени, чем незначительные изменения такого рода. Рабочая сила, оборудование и материалы — каждый из этих элементов оказывал бы свое влияние на производство совершенно независимо от состояния двух других; в частности, наличия двух элементов — рабочей силы и оборудования — было бы достаточно для выпуска продукции даже при полном отсутствии материалов. Линейные модели приемлемы во многих работах в области физики, но они не в состоянии отразить существенные характеристики промышленных и социальных процессов.

При помощи линейных моделей гораздо проще достигнуть конкретного математического решения, чем при помощи нелинейных. За незначительным исключением математический анализ не дает общих решений для нелинейных систем. Поэтому когда для приближенного отражения нелинейных по существу явлений используются линейные модели, то нелинейные характеристики этих явлений утрачиваются.

Как только мы отказываемся от попытки найти общее решение, которое описывало бы в едином комплексе все возможные характеристики поведения системы, сразу же исчезает различие в сложности исследования линейных и нелинейных систем. Методы моделирования, дающие частное решение для каждой отдельной совокупности условий, одинаково применимы для анализа как линейных, так и нелинейных систем.

Устойчивые и неустойчивые. Динамические модели, в которых условия меняются во времени, могут быть разделены на устойчивые и неустойчивые, точно так же, как и реальные системы, которые они отражают, можно охарактеризовать как устойчивые или неустойчивые.

Устойчивой является такая система, которая, будучи выведена из своего исходного состояния, стремится вернуться к нему. Она может колебаться некоторое время около исходной точки, подобно обычному маятнику, приведенному в движение, но возмущения в ней со временем затухают и исчезают.

В неустойчивой системе, находящейся первоначально в состоянии покоя, возникшее возмущение усиливается, вызывая увеличение значений соответствующих переменных или их колебания с возрастающей амплитудой. В нелинейной системе, которая при обычных условиях неустойчива, могут возникнуть колебания, возрастающие до тех пор, пока их не ограничит появление нелинейных по форме воздействий (недостаток рабочей силы, производственной мощности или же материальных ресурсов). Продолжающиеся колебания в этих условиях можно рассматривать как достигшие устойчивой амплитуды изменений от максимума до некоторого минимума. Очевидно, что в экономических системах максимальные уровни деловой активности ограничены ресурсами, а минимальные — нулевым ее значением.

Есть основания полагать, что производственно-сбытовые и экономические системы, представляющие для нас наибольший интерес, часто относятся к тому типу, в котором, как в неустойчивых системах, малые возмущения усиливаются до тех пор, пока не натолкнутся на нелинейные (по форме) ограничивающие факторы.

С устойчивым или меняющимся режимом. Модели (и системы) могут далее различаться в зависимости от того, является ли их поведение по своему характеру установившимся или изменчивым.

Модель с изменчивым режимом является цикличной, так что ее поведение в некоторый период времени носит тот же характер, что и в любой другой. С известной точки зрения модель неувеличивающейся национальной экономики, которая обнаруживает циклический характер деловой активности, можно считать колеблющейся в устойчивом режиме, несмотря на то что ни одна отдельно взятая последовательность событий никогда не повторяется совершенно одинаково. Точно так же при выяснении некоторых вопросов можно считать (как это делается в настоящее время с автомашинами), что длительный период эффективной эксплуатации определенного вида изделий можно представить в форме динамической модели с устойчивым режимом. В системах, относящихся к управлению хозяйственными организациями, устойчивый режим поведения представляет собой особый частный случай. (Система, рассматриваемая в главе 2, является динамической моделью с устойчивым режимом.)

Словесные модели — это описания предметов, явлений, событий, процессов на естественных языках.

Например, гелиоцентрическая модель мира, которую предложил Коперник, словесно описывалась следующим образом:

• Земля вращается вокруг своей оси и вокруг Солнца;
• все планеты движутся по орбитам, центром которых является Солнце.

Множество словесных моделей содержится в ваших школьных учебниках: в учебнике истории представлены модели исторических событий, в учебнике географии — модели географических объектов и природных процессов, в учебнике биологии — модели объектов животного и растительного мира.

Произведения художественной литературы — это тоже модели, так как они фиксируют внимание читателя на определённых сторонах человеческой жизни. Анализируя литературное произведение, вы выделяете в нём объекты и их свойства, отношения между героями, связи между событиями, проводите параллели с другими произведениями и т. п. Самое непосредственное отношение к понятию модели имеет такой литературный жанр, как басня. Смысл этого жанра состоит в переносе отношений между людьми на отношения между вымышленными персонажами, например животными.

1.2.2. Математические модели

Основным языком информационного моделирования в науке является язык математики.

Информационные модели, построенные с использованием математических понятий и формул, называются математическими моделями.

Язык математики представляет собой совокупность множества формальных языков; с некоторыми из них (алгебраическим, геометрическим) вы познакомились в школе, другие сможете узнать при дальнейшем обучении.

Язык алгебры позволяет формализовать функциональные зависимости между величинами, записав соотношения между количественными характеристиками объекта моделирования. В школьном курсе физики рассматривается много функциональных зависимостей, которые представляют собой математические модели изучаемых явлений или процессов.

Пример 1. Зависимость координаты тела от времени при прямолинейном равномерном движении имеет вид:

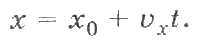
Изменение координаты тела х при прямолинейном равноускоренном движении в любой момент времени t выражается формулой:

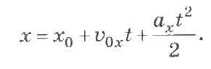
С помощью языка алгебры логики строятся логические модели — формализуются (записываются в виде логических выражений) простые и составные высказывания, выраженные на естественном языке. Путём построения логических моделей удаётся решать логические задачи, создавать логические модели устройств и т. д.

Пример 2. Рассмотрите электрические схемы (рис. 1.3).

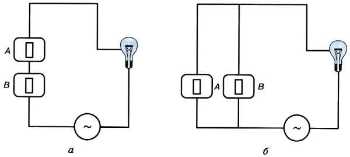
Рис. 1.3. Электрические схемы: а — последовательного и б — параллельного соединения переключателей

На них изображены известные вам из курса физики последовательное и параллельное соединения переключателей. В первом случае, чтобы лампочка загорелась, должны быть включены оба переключателя. Во втором случае достаточно, чтобы был включён один из переключателей.

Можно провести аналогию между элементами электрических схем и объектами и операциями алгебры логики:

Пусть голосу председателя соответствует переключатель А, голосам рядовых членов — переключатели В и С. Тогда F(A, В, C) = A & B & C ∨ A & B ∨ A & C.

Упростим полученное логическое выражение:

F(A, В, C) = A & B & (C ∨ 1) ∨ A & C = A & B & 1 ∨ A & C = A & B ∨ A & C = A & (B ∨ С).

Мы получили логическую модель, позволяющую построить схему проектируемой электрической цепи (рис. 1.4).

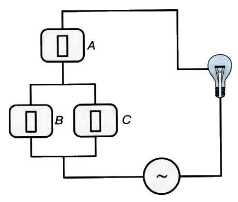
Рис. 1.4. Схема электрической цепи

1.2.3. Компьютерные математические модели

В настоящее время многие сложные математические модели могут быть реализованы 1 на компьютере. При этом используются такие средства, как:

• системы программирования;
• электронные таблицы;
• специализированные математические пакеты и программные средства для моделирования.

1 Реализация математической модели — это расчёт состояния (выходных параметров) моделируемой системы по формулам, связывающим её входные и выходные параметры.

Математические модели, реализованные с помощью систем программирования, электронных таблиц, специализированных математических пакетов и программных средств для моделирования, называются компьютерными математическими моделями.

Средства компьютерной графики позволяют визуализировать результаты расчётов, получаемых в процессе работы с компьютерными моделями.

Имитационные модели воспроизводят поведение сложных систем, элементы которых могут вести себя случайным образом.

САМОЕ ГЛАВНОЕ

Словесные модели — это описания предметов, явлений, событий, процессов на естественных языках.

Вопросы и задания

1. Ознакомьтесь с материалами презентации к параграфу, содержащейся в электронном приложении к учебнику. Что вы можете сказать о формах представления информации в презентации и в учебнике? Какими слайдами вы могли бы дополнить презентацию?

2. Приведите 2-3 собственных примера словесных моделей, рассматриваемых на уроках истории, географии, биологии.

4. Решите, составив математическую модель, следующую задачу.

Теплоход прошёл 4 км против течения реки, а затем прошёл ещё 33 км по течению, затратив на весь путь один час. Найдите собственную скорость теплохода, если скорость течения реки равна 6,5 км/ч.

6. Решите, составив логическую модель, следующую задачу.

На международных соревнованиях по прыжкам в воду первые пять мест заняли спортсмены из Германии, Италии, Китая, России и Украины. Ещё до начала соревнований эксперты высказали свои предположения об их итогах:

1) Первое место займёт спортсмен из Китая, а спортсмен из Украины будет третьим.
2) Украина будет на последнем месте, а Германия — на предпоследнем.
3) Германия точно будет четвёртой, а первое место займёт Китай.
4) Россия будет первой, а Италия — на втором месте.
5) Италия будет пятой, а победит Германия.

По окончании соревнований выяснилось, что каждый эксперт был прав только в одном утверждении. Какие места в соревновании заняли участники?

8. Приведите примеры использования компьютерных моделей. Найдите соответствующую информацию в сети Интернет.

Электронное приложение к уроку

Ссылки на ресурсы ЕК ЦОР

Ссылки на ресурсы ФЦИОР:

Презентации, плакаты, текстовые файлы

Вернуться к материалам урока

Ресурсы ЭОР

Cкачать материалы урока

Моделировать можно объект любой природы и любой сложности. И как раз сложные объекты представляют наибольший интерес для моделирования; именно здесь моделирование может дать результаты, которые нельзя получить другими способами исследования.

Главная особенность моделирования в том, что этот метод опосредованного познания с помощью объектов – заместителей. Модель выступает как своеобразный инструмент познания, который исследователь ставит между собой и объектом, и с помощью которого изучает интересующий его объект.

Необходимость использования метода моделирования определяется тем, что многие объекты непосредственно исследовать или невозможно, или же это исследование требует много времени и средств.

Вложение	Размер
npk.doc	144.5 КБ

Предварительный просмотр:

Муниципальное бюджетное образовательное учреждение

Елабужского муниципального района

в теории и в жизни

ученица 8 класса

II. Экспериментальное исследование с использованием приемов математического моделирования………………………………………………………………………..….8

Решая математические задачи из учебника, они строят математическую модель.

Алгебра в основном занимается тем, что описывает реальные различные ситуации на математическом языке в виде математических моделей, а затем имеет дело уже не с реальными ситуациями, а с этими моделями, используя разные правила, свойства, законы, выработанные в алгебре.

В данной работе были поставлены следующие задачи:

- изучить научно-популярную литературу по данному вопросу;

Моделирование в научных исследованиях стало применяться еще в глубокой древности и постепенно захватывало все новые области знаний:

Большие успехи и признание практически во всех отраслях современной науки принес методу моделирования ХХ век. Однако методология моделирования долгое время развивалась независимо отдельными науками. Отсутствовала единая система понятий, единая терминология. Лишь постепенно стала осознаваться роль моделирования как универсального метода научного познания.

Под моделированием понимается процесс построения, изучения и применения моделей. Оно тесно связано с такими категориями, как абстракция, аналогия, гипотеза и др. Процесс моделирования обязательно включает и построение абстракций, и умозаключения по аналогии, и конструирование научных гипотез.

Процесс моделирования включает три элемента:

Cубъект (исследователь);
Объект исследования;
Модель, опосредствующую отношения познающего субъекта и познаваемого объекта.

Для математического исследования процессов и явлений, реально происходящих в действительности, надо суметь описать их на языке математики, т.е. построить математическую модель процесса, явления. Математические модели и являются объектами непосредственного математического исследования.

Математической моделью называют описание какого-либо реального процесса или некоторой исследуемой ситуации на языке математических понятий, формул и отношений.

Математическая модель - это упрощенный вариант действительности, используемый для изучения ее ключевых свойств. "Математическая модель, основанная на некотором упрощении, идеализации, не тождественна объекту, а является его приближённым отражением. Однако благодаря замене реального объекта соответствующей ему моделью появляется возможность сформулировать задачу его изучения как математическую и воспользоваться для анализа универсальным математическим аппаратом, который не зависит от конкретной природы объекта". Чарльз Лейв и Джеймс Марч дают такое определение модели: “Модель - это упрощенная картина реального мира. Она обладает некоторыми, но не всеми свойствами реального мира. Она представляет собой множество взаимосвязанных предположений о мире. Модель проще тех явлений, которые она по замыслу отображает или объясняет". В настоящее время построение, исследование и приложение математических моделей является, можно сказать, основным предметом деятельности математиков.

Пусть имеется или необходимо создать некоторый объект А. Мы конструируем (материально или мысленно) или находим в реальном мире другой объект В – модель объекта А.

Модель утрачивает свой смысл как в случае тождества с оригиналом, так и в случае чрезмерного во всех существенных отношениях отличия от оригинала. Изучение одних сторон моделируемого объекта осуществляется ценой отказа от отражения других сторон. Поэтому любая модель замещает оригинал лишь в строго ограниченном смысле. Из этого следует, что для одного объекта может быть построено несколько специализированных моделей.

Можно выделить несколько основных этапов процессов моделирования.

Первый этап - постановка проблемы и ее качественный анализ. Главное здесь – четко сформулировать сущность проблемы. Этот этап включает выделение важнейших черт и свойств моделируемого объекта, изучение структуры объекта, объясняющих поведение и развитие объекта.

На третьем этапе осуществляется перенос знаний с модели на оригинал – формирование множества знаний об объекте. Мы можем переносить какой-либо результат с модели на оригинал, если этот результат связан с признаками сходства оригинала и модели.

Следующий этап – численное решение. Этот этап включает разработку численного решения задачи, составление программ и непосредственное проведение расчетов.

Последний этап – анализ численных результатов и применение. На этом заключительном этапе встает вопрос о правильности и полноте результатов моделирования, о степени практической применимости последних.

Математическое моделирование — это процесс построения и изучения математических моделей.

Все естественные и общественные науки, использующие математический аппарат, по сути занимаются математическим моделированием: заменяют объект его математической моделью и затем изучают последнюю. Связь математической модели с реальностью осуществляется с помощью цепочки гипотез, идеализаций и упрощений. С помощью математических методов описывается, как правило, идеальный объект, построенный на этапе содержательного моделирования.

Содержание

Определения

Никакое определение не может в полном объёме охватить реально существующую деятельность по математическому моделированию. Несмотря на это, определения полезны тем, что в них делается попытка выделить наиболее существенные черты.

Определение модели по А. А. Ляпунову: Моделирование — это опосредованное практическое или теоретическое исследование объекта, при котором непосредственно изучается не сам интересующий нас объект, а некоторая вспомогательная искусственная или естественная система (модель):

находящаяся в некотором объективном соответствии с познаваемым объектом;
способная замещать его в определенных отношениях;
дающая при её исследовании, в конечном счете, информацию о самом моделируемом объекте. [2]

Классификация моделей

Формальная классификация моделей

Формальная классификация моделей основывается на классификации используемых математических средств. Часто строится в форме дихотомий. Например, один из популярных наборов дихотомий [9] :

и так далее. Каждая построенная модель является линейной или нелинейной, детерминированной или стохастической, … Естественно, что возможны и смешанные типы: в одном отношении сосредоточенные (по части параметров), в другом — распределённые модели и т. д.

Классификация по способу представления объекта

Наряду с формальной классификацией, модели различаются по способу представления объекта:

Содержательные и формальные модели

Практически все авторы, описывающие процесс математического моделирования, указывают, что сначала строится особая идеальная конструкция, содержательная модель [14] . Устоявшейся терминологии здесь нет, и другие авторы называют этот идеальный объект концептуальная модель [15] , умозрительная модель [16] или предмодель [17] . При этом финальная математическая конструкция называется формальной моделью или просто математической моделью, полученной в результате формализации данной содержательной модели (предмодели). Построение содержательной модели может производиться с помощью набора готовых идеализаций, как в механике, где идеальные пружины, твёрдые тела, идеальные маятники, упругие среды и т. п. дают готовые структурные элементы для содержательного моделирования. Однако в областях знания, где не существует полностью завершенных формализованных теорий (передний край физики, биологии, экономики, социологии, психологии, и большинства других областей), создание содержательных моделей резко усложняется.

Содержательная классификация моделей

В работе Р. Пайерлса [18] дана классификация математических моделей, используемых в физике и, шире, в естественных науках. В книге А. Н. Горбаня и Р. Г. Хлебопроса [19] эта классификация проанализирована и расширена. Эта классификация сфокусирована, в первую очередь, на этапе построения содержательной модели.

Тип 1: Гипотеза (такое могло бы быть)

Никакая гипотеза в науке не бывает доказана раз и навсегда. Очень чётко это сформулировал Ричард Фейнман:

Если модель первого типа построена, то это означает, что она временно признаётся за истину и можно сконцентрироваться на других проблемах. Однако это не может быть точкой в исследованиях, но только вре́менной паузой: статус модели первого типа может быть только вре́менным.

Тип 2: Феноменологическая модель (ведем себя так, как если бы…)

Роль модели в исследовании может меняться со временем, может случиться так, что новые данные и теории подтвердят феноменологические модели и те будут повышены до статуса гипотезы. Аналогично, новое знание может постепенно прийти в противоречие с моделями-гипотезами первого типа и те могут быть переведены во второй. Так, кварковая модель постепенно переходит в разряд гипотез; атомизм в физике возник как временное решение, но с ходом истории перешёл в первый тип. А вот модели эфира, проделали путь от типа 1 к типу 2, а сейчас находятся вне науки.

Идея упрощения очень популярна при построении моделей. Но упрощение бывает разным. Пайерлс выделяет три типа упрощений в моделировании.

Тип 3: Приближение (что-то считаем очень большим или очень малым)

Если можно построить уравнения, описывающие исследуемую систему, то это не значит, что их можно решить даже с помощью компьютера. Общепринятый прием в этом случае — использование приближений (моделей типа 3). Среди них модели линейного отклика. Уравнения заменяются линейными. Стандартный пример — закон Ома.

Если мы используем модель идеального газа для описания достаточно разреженных газов, то это — модель типа 3 (приближение). При более высоких плотностях газа тоже полезно представлять себе более простую ситуацию с идеальным газом для качественного понимания и оценок, но тогда это уже тип 4.

Тип 4: Упрощение (опустим для ясности некоторые детали)

Примеры: применение модели идеального газа к неидеальному, уравнение состояния Ван-дер-Ваальса, большинство моделей физики твердого тела, жидкостей и ядерной физики. Путь от микроописания к свойствам тел (или сред), состоящих из большого числа частиц, очень длинен. Приходится отбрасывать многие детали. Это приводит к моделям 4-го типа.

Тип 5: Эвристическая модель (количественного подтверждения нет, но модель способствует более глубокому проникновению в суть дела)

Но при построении новой физики далеко не сразу получается модель, дающая хотя бы качественное описание объекта — модель пятого типа. В этом случае часто используют модель по аналогии, отражающую действительность хоть в какой-нибудь черте.

Тип 6: Аналогия (учтём только некоторые особенности)

Тип 7: Мысленный эксперимент (главное состоит в опровержении возможности)

А. Эйнштейн был одним из великих мастеров мысленного эксперимента. Вот один из его экспериментов. Он был придуман в юности и, в конце концов, привел к построению специальной теории относительности. Предположим, что в классической физике мы движемся за световой волной со скоростью света. Мы будем наблюдать периодически меняющееся в пространстве и постоянное во времени электромагнитное поле. Согласно уравнениям Максвелла, этого быть не может. Отсюда юный Эйнштейн заключил: либо законы природы меняются при смене системы отсчета, либо скорость света не зависит от системы отсчета. Он выбрал второй — более красивый вариант. Другой знаменитый мысленный эксперимент Эйнштейна — Парадокс Эйнштейна — Подольского — Розена.

А вот и тип 8, широко распространенный в математических моделях биологических систем.

Тип 8: Демонстрация возможности (главное — показать внутреннюю непротиворечивость возможности)

Это тоже мысленные эксперименты с воображаемыми сущностями, демонстрирующие, что предполагаемое явление согласуется с базовыми принципам и внутренне непротиворечиво. В этом основное отличие от моделей типа 7, которые вскрывают скрытые противоречия.

В основе содержательной классификации — этапы, предшествующие математическому анализу и вычислениям. Восемь типов моделей по Р. Пайерлсу суть восемь типов исследовательских позиций при моделировании.

Пример

Рассмотрим механическую систему, состоящую из пружины, закрепленной с одного конца, и груза массой , прикрепленного к свободному концу пружины. Будем считать, что груз может двигаться только в направлении оси пружины (например, движение происходит вдоль стержня). Построим математическую модель этой системы. Будем описывать состояние системы расстоянием от центра груза до его положения равновесия. Опишем взаимодействие пружины и груза с помощью закона Гука () после чего воспользуемся вторым законом Ньютона, чтобы выразить его в форме дифференциального уравнения:

$m\ddot x=-kx,$

где означает вторую производную от по времени: " width="" height="" />
.

По формальной классификации эта модель линейная, детерминисткая, динамическая, сосредоточенная, непрерывная. В процессе её построения мы сделали множество допущений (об отсутствии внешних сил, отсутствии трения, малости отклонений и т. д.), которые в реальности могут не выполняться.

Жёсткие и мягкие модели

$m\ddot x=-kx+\varepsilon f(x,\dot x),$

Здесь — некоторая функция, в которой может учитываться сила трения или зависимость коэффициента жёсткости пружины от степени её растяжения, — некоторый малый параметр. Явный вид функции нас в данный момент не интересует. Если мы докажем, что поведение мягкой модели принципиально не отличается от поведения жёсткой (вне зависимости от явного вида возмущающих факторов, если они достаточно малы), задача сведется к исследованию жёсткой модели. В противном случае применение результатов, полученных при изучении жёсткой модели, потребует дополнительных исследований. Например, решением уравнения гармонического осциллятора являются функции вида t+ B \cos \sqrtt" width="" height="" />
, то есть колебания с постоянной амплитудой. Следует ли из этого, что реальный осциллятор будет бесконечно долго колебаться с постоянной амплитудой? Нет, поскольку рассматривая систему со сколь угодно малым трением (всегда присутствующим в реальной системе), мы получим затухающие колебания. Поведение системы качественно изменилось.

Если система сохраняет свое качественное поведение при малом возмущении, говорят, что она структурно устойчива. Гармонический осциллятор — пример структурно-неустойчивой (негрубой) системы. [21] Тем не менее, эту модель можно применять для изучения процессов на ограниченных промежутках времени.

Универсальность моделей

Прямая и обратная задачи математического моделирования

Существует множество задач, связанных с математическим моделированием. Во-первых, надо придумать основную схему моделируемого объекта, воспроизвести его в рамках идеализаций данной науки. Так, вагон поезда превращается в систему пластин и более сложных тел из разных материалов, каждый материал задается как его стандартная механическая идеализация (плотность, модули упругости, стандартные прочностные характеристики), после чего составляются уравнения, по дороге какие-то детали отбрасываются, как несущественные, производятся расчёты, сравниваются с измерениями, модель уточняется, и так далее. Однако для разработки технологий математического моделирования полезно разобрать этот процесс на основные составные элементы.

Традиционно выделяют два основных класса задач, связанных с математическими моделями: прямые и обратные.

Прямая задача: структура модели и все её параметры считаются известными, главная задача — провести исследование модели для извлечения полезного знания об объекте. Какую статическую нагрузку выдержит мост? Как он будет реагировать на динамическую нагрузку (например, на марш роты солдат, или на прохождение поезда на различной скорости), как самолёт преодолеет звуковой барьер, не развалится ли он от флаттера, — вот типичные примеры прямой задачи. Постановка правильной прямой задачи (задание правильного вопроса) требует специального мастерства. Если не заданы правильные вопросы, то мост может обрушиться, даже если была построена хорошая модель для его поведения. Так, в 1879 г. в Великобритании обрушился металлический мост через реку Тей, конструкторы которого построили модель моста, рассчитали его на 20-кратный запас прочности на действие полезной нагрузки, но забыли о постоянно дующих в тех местах ветрах. И через полтора года он рухнул. [22]

В простейшем случае (одно уравнение осциллятора, например) прямая задача очень проста и сводится к явному решению этого уравнения.

Обратная задача: известно множество возможных моделей, надо выбрать конкретную модель на основании дополнительных данных об объекте. Чаще всего, структура модели известна, и необходимо определить некоторые неизвестные параметры. Дополнительная информация может состоять в дополнительных эмпирических данных, или в требованиях к объекту (задача проектирования). Дополнительные данные могут поступать независимо от процесса решения обратной задачи (пассивное наблюдение) или быть результатом специально планируемого в ходе решения эксперимента (активное наблюдение).

Одним из первых примеров виртуозного решения обратной задачи с максимально полным использованием доступных данных был построенный И. Ньютоном метод восстановления сил трения по наблюдаемым затухающим колебаниям.

В качестве другого примера можно привести математическую статистику. Задача этой науки — разработка методов регистрации, описания и анализа данных наблюдений и экспериментов с целью построения вероятностных моделей массовых случайных явлений [23] . Т.е. множество возможных моделей ограничено вероятностными моделями. В конкретных задачах множество моделей ограничено сильнее.

Компьютерные системы моделирования

Для поддержки математического моделирования разработаны системы компьютерной математики, например, Maple, Mathematica, Mathcad, MATLAB, VisSim и др. [24] Они позволяют создавать формальные и блочные модели как простых, так и сложных процессов и устройств и легко менять параметры моделей в ходе моделирования. Блочные модели представлены блоками (чаще всего графическими), набор и соединение которых задаются диаграммой модели.

Дополнительные примеры

Модель Мальтуса

Скорость роста пропорциональна текущему размеру популяции. Она описывается дифференциальным уравнением

$\dot x= \alpha x,$

где — некоторый параметр, определяемый разностью между рождаемостью и смертностью. Решением этого уравнения является экспоненциальная функция " width="" height="" />
. Если рождаемость превосходит смертность (), размер популяции неограниченно и очень быстро возрастает. Понятно, что в действительности этого не может происходить из-за ограниченности ресурсов. При достижении некоторого критического объёма популяции модель перестает быть адекватной, поскольку не учитывает ограниченность ресурсов. Уточнением модели Мальтуса может служить логистическая модель, которая описывается дифференциальным уравнением Ферхюльста

$\dot x=\alpha \left( 1-\frac<x></p> <p>> \right) x,$

Система хищник-жертва

Допустим, что на некоторой территории обитают два вида животных: кролики (питающиеся растениями) и лисы (питающиеся кроликами). Пусть число кроликов , число лис . Используя модель Мальтуса с необходимыми поправками, учитывающими поедание кроликов лисами, приходим к следующей системе, носящей имя модели Лотки — Вольтерра:

$\begin</p> <p> \dot x=(\alpha -c y)x;\\ \dot y=(-\beta+d x) y. \end$

Эта система имеет равновесное состояние, когда число кроликов и лис постоянно. Отклонение от этого состояния приводит к колебаниям численности кроликов и лис, аналогичным колебаниям гармонического осциллятора. Как и в случае гармонического осциллятора, это поведение не является структурно устойчивым: малое изменение модели (например, учитывающее ограниченность ресурсов, необходимых кроликам) может привести к качественному изменению поведения. Например, равновесное состояние может стать устойчивым, и колебания численности будут затухать. Возможна и противоположная ситуация, когда любое малое отклонение от положения равновесия приведет к катастрофическим последствиям, вплоть до полного вымирания одного из видов. На вопрос о том, какой из этих сценариев реализуется, модель Вольтерра — Лотки ответа не дает: здесь требуются дополнительные исследования.

Читайте также: