Сообщение на тему решение комбинаторных задач

Обновлено: 17.04.2024

Комбинаторика – раздел математики, который изучает задачи выбора и расположения элементов из некоторого основного множества в соответствии с заданными правилами. Формулы и принципы комбинаторики используются в теории вероятностей для подсчета вероятности случайных событий и, соответственно, получения законов распределения случайных величин. Это, в свою очередь, позволяет исследовать закономерности массовых случайных явлений, что является весьма важным для правильного понимания статистических закономерностей, проявляющихся в природе и технике.

Правила сложения и умножения в комбинаторике

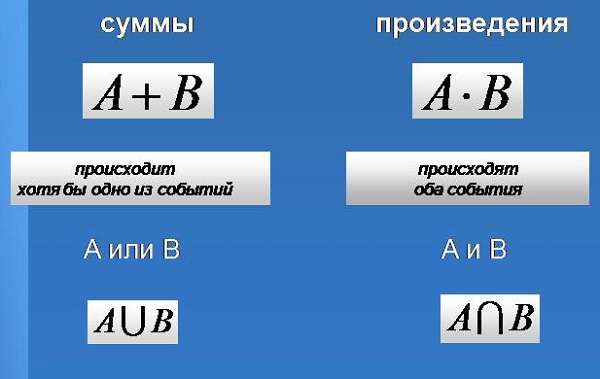
Правило суммы. Если два действия А и В взаимно исключают друг друга, причем действие А можно выполнить m способами, а В – n способами, то выполнить одно любое из этих действий (либо А, либо В) можно n + m способами.

Пример 1.

В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить одного дежурного?

Дежурным можно назначить либо мальчика, либо девочку, т.е. дежурным может быть любой из 16 мальчиков, либо любая из 10 девочек.

По правилу суммы получаем, что одного дежурного можно назначить 16+10=26 способами.

Правило произведения. Пусть требуется выполнить последовательно k действий. Если первое действие можно выполнить n₁ способами, второе действие n₂ способами, третье – n₃ способами и так до k-го действия, которое можно выполнить n_k способами, то все k действий вместе могут быть выполнены:

Пример 2.

В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить двух дежурных?

Первым дежурным можно назначить либо мальчика, либо девочку. Т.к. в классе учится 16 мальчиков и 10 девочек, то назначить первого дежурного можно 16+10=26 способами.

После того, как мы выбрали первого дежурного, второго мы можем выбрать из оставшихся 25 человек, т.е. 25-ю способами.

По теореме умножения двое дежурных могут быть выбраны 26*25=650 способами.

Сочетания без повторений. Сочетания с повторениями

Классической задачей комбинаторики является задача о числе сочетаний без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать m из n различных предметов ?

Пример 3.

Необходимо выбрать в подарок 4 из 10 имеющихся различных книг. Сколькими способами можно это сделать?

Нам из 10 книг нужно выбрать 4, причем порядок выбора не имеет значения. Таким образом, нужно найти число сочетаний из 10 элементов по 4:

Рассмотрим задачу о числе сочетаний с повторениями: имеется по r одинаковых предметов каждого из n различных типов; сколькими способами можно выбрать m () из этих (n*r) предметов?

Пример 4.

В кондитерском магазине продавались 4 сорта пирожных: наполеоны, эклеры, песочные и слоеные. Сколькими способами можно купить 7 пирожных?

Т.к. среди 7 пирожных могут быть пирожные одного сорта, то число способов, которыми можно купить 7 пирожных, определяется числом сочетаний с повторениями из 7 по 4.

Размещения без повторений. Размещения с повторениями

Классической задачей комбинаторики является задача о числе размещений без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать и разместить по m различным местам m из n различных предметов?

Пример 5.

В некоторой газете 12 страниц. Необходимо на страницах этой газеты поместить четыре фотографии. Сколькими способами можно это сделать, если ни одна страница газеты не должна содержать более одной фотографии?

В данной задаче мы не просто выбираем фотографии, а размещаем их на определенных страницах газеты, причем каждая страница газеты должна содержать не более одной фотографии. Таким образом, задача сводится к классической задаче об определении числа размещений без повторений из 12 элементов по 4 элемента:

Таким образом, 4 фотографии на 12 страницах можно расположить 11880 способами.

Также классической задачей комбинаторики является задача о числе размещений с повторениями, содержание которой можно выразить вопросом: сколькими способами можно выбрать и разместить по m различным местам m из n предметов, среди которых есть одинаковые?

Пример 6.

У мальчика остались от набора для настольной игры штампы с цифрами 1, 3 и 7. Он решил с помощью этих штампов нанести на все книги пятизначные номера– составить каталог. Сколько различных пятизначных номеров может составить мальчик?

Можно считать, что опыт состоит в 5-кратном выборе с возращением одной из 3 цифр (1, 3, 7). Таким образом, число пятизначных номеров определяется числом размещений с повторениями из 3 элементов по 5:

Перестановки без повторений. Перестановки с повторениями

Классической задачей комбинаторики является задача о числе перестановок без повторения, содержание которой можно выразить вопросом: сколькими способами можно разместить n различных предметов на n различных местах?

Пример 7.

Для случая, когда среди выбираемых n элементов есть одинаковые (выборка с возвращением), задачу о числе перестановок с повторениями можно выразить вопросом: сколькими способами можно переставить n предметов, расположенных на n различных местах, если среди n предметов имеются k различных типов (k

Пример 8.

Предмет комбинаторики (теории вероятностей), как отрасли программирования. Краткая историческая справка о ее зарождении и развитии. Комбинаторные задачи, варианты и способы их решения. Основные формулы комбинаторики, правила произведений и суммы.

Рубрика	Программирование, компьютеры и кибернетика
Вид	реферат
Язык	русский
Дата добавления	15.06.2014
Размер файла	22,1 K

Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.

Содержание

1. Предмет комбинаторики

2. Краткая историческая справка

3. Основные комбинаторные задачи

4. Основные формулы комбинаторики

5. Правило произведений

6. Правило суммы

Список использованной литературы

Введение

Задачи дискретной математики, к которым относится большинство олимпиадных задач по информатике, часто сводятся к перебору различных комбинаторных конфигураций объектов и выбору среди них наилучшего, с точки зрения условия той или иной задачи. Поэтому знание алгоритмов генерации наиболее распространенных комбинаторных конфигураций является необходимым условием успешного решения олимпиадных задач в целом. Важно также знать количество различных вариантов для каждого типа комбинаторных конфигураций, так как это позволяет реально оценить вычислительную трудоемкость выбранного алгоритма решения той или иной задачи.

1. Предмет комбинаторики

Наблюдаемые нами события (явления) можно подразделить на следующие три вида: достоверные, невозможные и случайные.

По-иному обстоит дело, если рассматриваются случайные события, которые могут многократно наблюдаться при осуществлении одних и тех же условий S, т. е. если речь идет о массовых однородных случайных событиях. Оказывается, что достаточно большое число однородных случайных событий независимо от их конкретной природы подчиняется определенным закономерностям, а именно вероятностным закономерностям. Установлением этих закономерностей и занимается теория вероятностей.

Итак, предметом теории вероятностей является изучение вероятностных закономерностей массовых однородных случайных событий.

В последние годы методы теории вероятностей все шире и шире проникают в различные области науки и техники, способствуя их прогрессу.

2. Краткая историческая справка

Первые работы, в которых зарождались основные понятия теории вероятностей, представляли собой попытки создания теории азартных игр (Кардано, Гюйгенс, Паскаль, Ферма и другие в XVI--XVII вв.).

Дальнейшими успехами теория вероятностей обязана Муавру, Лапласу, Гауссу, Пуассону и др.

Новый, наиболее плодотворный период связан с именами П. Л. Чебышева (1821--1894) и его учеников А.А.Маркова(1856--1922) и А. М.Ляпунова (1857--1918). В этот период теория вероятностей становится стройной математической наукой. Ее последующее развитие обязано в первую очередь русским и советским математикам (С. Н. Бернштейн, В. И. Романовский, А. Н. Колмогоров, А. Я. Хинчин, Б. В. Гнеденко, Н. В. Смирнов и др.). В настоящее время ведущая роль в создании новых ветвей теории вероятностей также принадлежит советским математикам.

3. Основные комбинаторные задачи

Основными и типичными операциями и связанными с ними задачами комбинаторики являются следующие:

1) образование упорядоченных множеств, состоящее в установлении определенного порядка следования элементов множества друг за другом, - составление перестановок;

2) образование подмножеств, состоящее в выделении из данного множества некоторой части его элементов, - составление сочетаний;

3) образование упорядоченных подмножеств - составление размещений.

ТИПЫ КОМБИНАТОРНЫХ ЗАДАЧ.

1. Магический квадрат - квадратная таблица (n * n) целых чисел от 1 до n¤ такая, что суммы чисел вдоль любого столбца, любой строки и двух диагоналей таблицы равны одному и тому же числу s=n(n¤+1)/2. Число n называют порядом магического квадрата.

Доказано, что магический квадрат можно построить для любого n Є 3. Уже в средние века был известен алгоритм построения магических квадратов нечетного порядка. Существуют магические квадраты, удоволетворяющие ряду дополнительных условий, например магический квадрат с n=8 , который можно разделить на четыре меньших магических квадрата 4x4. В Индии и некоторых других странах магические квадраты употреблялись как талисманы. Однако общей теории магических квадратов не существует. Неизвестно даже общее число магических квадратов порядка n.

2. Латинский квадрат - квадратная матрица порядка n, каждая строка и каждый столбец которой являются перестановками элементов конечного множества S, состоящего из n элементов.

3. Задача размещения - одна из классических комбинаторных задач, в которой требуется определить число способов размещения m различных предметов в n различных ячейках с заданным числом r пустых ячеек. Это число равно

r n-r mC (r)=C дельта O , r=0,1,2. n,nm n

k m k j j m дельта O =сигма (-1) C (k-j) j=0 k

Задача коммивояжера, задача о бродячем торговце - комбинаторная задача теории графов. В простейшем случае формулируется следующим образом: даны n городов и известно расстояние между каждыми двумя городами; коммивояжер, выходящий из какого-нибудь города, должен посетить n-1 других городов и вернуться в исходный. В каком порядке должен он посещать города (по одному разу каждый) чтобы общее пройденное расстояние было минимальным?

Методы решения задачи коммивояжера, по существу, сводятся к организации полного перебора вариантов.

МЕТОДЫ РЕШЕНИЯ КОМБИНАТОРНЫХ ЗАДАЧ

1. Метод рекуррентных соотношений.

Метод рекуррентных соотношений состоит в том, что решение комбинаторной задачи с n предметами выражается через решение аналогичной задачи с меньшим числом предметов с помощью некоторого соотношения, которое называется рекуррентным. Пользуясь этим соотношением, искомую величину можно вычислить, исходя из того, что для небольшого количества предметов решение задачи легко находится.

2. Метод включения и исключения.

Пусть N(A) - число элементов множества A. Тогда методом математической индукции можно доказать, что

Метод подсчета числа элементов объединения множеств по этой формуле, состоящий в поочередном сложении и вычитании, называется методом включения и исключения.

3. Метод траекторий.

Для многих комбинаторных задач можно указать такую геометрическую интерпретацию, которая сводит задачу к подсчету числа путей (траекторий), обладающих определенным свойством.

4. Основные формулы комбинаторики

Комбинаторика изучает количества комбинаций, подчиненных определенным условиям, которые можно составить из элементов, безразлично какой природы, заданного конечного множества. При непосредственном вычислении вероятностей часто используют формулы комбинаторики. Приведем наиболее употребительные из них.

Перестановками называют комбинации, состоящие из одних и тех же n различных элементов и отличающиеся только порядком их расположения. Число всех возможных перестановок

где n! = 1 * 2 * 3 . n.

Заметим, что удобно рассматривать 0!, полагая, по определению, 0! = 1.

Размещениями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются либо составом элементов, либо их порядком. Число всех возможных размещений

A m _n = n (n - 1)(n - 2) . (n - m + 1).

Сочетаниями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются хотя бы одним элементом. Число сочетаний

примеры перестановок, размещений, сочетаний

Подчеркнем, что числа размещений, перестановок и сочетаний связаны равенством

Замечание. Выше предполагалось, что все n элементов различны. Если же некоторые элементы повторяются, то в этом случае комбинации с повторениями вычисляют по другим формулам. Например, если среди n элементов есть n₁ элементов одного вида, n₂ элементов другого вида и т.д., то число перестановок с повторениями

5. Правило произведения

Если объект А можно выбрать из совокупности объектов m способами и после каждого такого выбора объект В можно выбрать n способами, то пара объектов (А, В) в указанном порядке может быть выбрана mn способами.

Произведение событий. Произведением двух событий А и В называют событие АВ, состоящее в совместном появлении (совмещении) этих событий. Например, если А -- деталь годная, В -- деталь окрашенная, то АВ -- деталь годна и окрашена.

Условная вероятность. Во введении случайное событие определено как событие, которое при осуществлении совокупности условий S может произойти или не произойти. Если при вычислении вероятности события никаких других ограничений, кроме условий S, не налагается, то такую вероятность называют безусловной; если же налагаются и другие дополнительные условия, то вероятность события называют условной. Например, часто вычисляют вероятность события В при дополнительном условии, что произошло событие А. Заметим, что и безусловная вероятность, строго говоря, является условной, поскольку предполагается осуществление условий S.

Условной вероятностью Р_A (В) называют вероятность события В, вычисленную в предположении, что событие А уже наступило.

Исходя из классического определения вероятности, формулу Р_A (В) = Р (АВ) / Р (А) (Р (А) > 0 можно доказать. Это обстоятельство и служит основанием для следующего общего (применимого не только для классической вероятности) определения.

Условная вероятность события В при условии, что событие А уже наступило, по определению, равна

Рассмотрим два события: А и В; пусть вероятности Р (А) и Р_A (В) известны. Как найти вероятность совмещения этих событий, т. е. вероятность того, что появится и событие А и событие В? Ответ на этот вопрос дает теорема умножения.

6. Правило суммы

Если некоторый объект А может быть выбран из совокупности объектов m способами, а другой объект В может быть выбран n способами, то выбрать либо А, либо В можно m + n способами.

Суммой А + В двух событий А и В называют событие, состоящее в появлении события А, или события В, или обоих этих событий. Например, если из орудия произведены два выстрела и А -- попадание при первом выстреле, В -- попадание при втором выстреле, то А + В -- попадание при первом выстреле, или при втором, или в обоих выстрелах.

В частности, если два события А и B -- несовместные, то А + В -- событие, состоящее в появлении одного из этих событий, безразлично какого.

Суммой нескольких событий называют событие, которое состоит в появлении хотя бы одного из этих событий. Например, событие А + В + С состоит в появлении одного из следующих событий: А, В, С, А и В, А и С, В и С, А и В и С.

Пусть события A и В -- несовместные, причем вероятности этих событий известны. Как найти вероятность того, что наступит либо событие A, либо событие В? Ответ на этот вопрос дает теорема сложения.

Теорема. Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий:

Р (А + В) = Р (А) + Р (В).

Введем обозначения: n -- общее число возможных элементарных исходов испытания; m₁ -- число исходов, благоприятствующих событию A; m₂-- число исходов, благоприятствующих событию В.

Число элементарных исходов, благоприятствующих наступлению либо события А, либо события В, равно m₁ + m₂. Следовательно,

Приняв во внимание, что m₁ / n = Р (А) и m₂ / n = Р (В), окончательно получим

Р (А + В) = Р (А) + Р (В).

Следствие. Вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий:

Рассмотрим три события: А, В и С. Так как рассматриваемые события попарно несовместны, то появление одного из трех событий, А, В и С, равносильно наступлению одного из двух событий, A + В и С, поэтому в силу указанной теоремы

Р ( А + В + С) = Р [(А + В) + С] = Р (А + В) + Р (С) = Р (А) + Р (В) + Р (С)

Заключение

Перечисленные подзадачи в программировании обычно рассматривают для следующих комбинаторных конфигураций: перестановки элементов множества, подмножества множества, сочетания из n элементов множества по k элементов (k-элементные подмножества множества, состоящего из nk элементов), размещения (упорядоченные подмножества множества, то есть отличающиеся не только составом элементов, но и порядком элементов в них), разбиения множества (множество разбивается на подмножества произвольного размера так, что каждый элемент исходного множества содержится ровно в одном подмножестве), разбиения натуральных чисел на слагаемые, правильные скобочные последовательности (различные правильные взаимные расположения n пар открывающихся и закрывающихся скобок).

Большинство указанных конфигураций были подробно рассмотрены в 2. Однако при генерации различных конфигураций использовались в основном нерекурсивные алгоритмы. Опытные же участники олимпиад в подобных случаях при программировании используют в основном именно рекурсию, с помощью которой решение рассматриваемых задач зачастую можно записать более кратко и прозрачно. Поэтому для полноты изложения данной темы приведем ряд рекурсивных комбинаторных алгоритмов и рассмотрим особенности применения рекурсии в комбинаторике.

комбинаторика вероятность исторический программирование

Список использованной литературы

Окулов С.М. Перестановки. “Информатика”, №7, 2000.

Окулов С.M. Комбинаторные задачи. “Информатика”, №10, 13, 2000.

Усов Б.Б. Комбинаторные задачи. “Информатика”, №39, 2000.

Кормен Т., Лейзерсон Ч., Ривест Р. Алгоритмы. Построение и анализ. М.: МЦНМО, 2000.

Брудно A.Л., Каплан Л.И. Московские олимпиады по программированию. М.: Наука, 1990.

Кнут Д. Конкретная математика. Основание информатики. М.: “Мир”, 1998.

Липский В. Комбинаторика для программистов. М.: “Мир”, 1988.

Андреева Е.В. Еще раз о задачах на полный перебор вариантов. “Информатика”, №45, 2000.

Подобные документы

Предмет, постановка и особенности задач дискретного программирования. Задачи с неделимостями и с разрывными целевыми функциями. Экстремальные комбинаторные задачи. Примеры решений задач дискретного программирования методом ветвей и границ, методом Гомори.

курсовая работа [211,3 K], добавлен 22.05.2013

Исследование методов решения задачи о ходе коня. Описание алгоритмов для итеративной и рекурсивной программ. Генерация перестановок элементов по индексам. Построение эйлерова цикла на графе. Поиск кратчайшего пути на графе. Программная реализация задачи.

курсовая работа [411,6 K], добавлен 25.04.2013

Применение методов линейного программирования для решения оптимизационных задач. Основные понятия линейного программирования, свойства транспортной задачи и теоремы, применяемые для ее решения. Построение первичного опорного плана и системы потенциалов.

курсовая работа [280,8 K], добавлен 17.11.2011

Теоретическая основа линейного программирования. Задачи линейного программирования, методы решения. Анализ оптимального решения. Решение одноиндексной задачи линейного программирования. Постановка задачи и ввод данных. Построение модели и этапы решения.

курсовая работа [132,0 K], добавлен 09.12.2008

Решение задач по информатике, перебор различных комбинаторных конфигураций объектов и выбор наилучшего, с точки зрения условия задачи. Генерация k-элементных подмножеств, всех подмножеств данного множества, всех перестановок n-элементного множества.

Комбинаторика — раздел математики. Основные понятия и формулы комбинаторики как науки применяются во всех сферах жизни.

Неудивительно, что она включена в программу 11 класса, а также во вступительные испытания во многих ВУЗах РФ. Ее основы лежат в прикладном искусстве многих сфер деятельности человека.

Ее история насчитывает более 6 веков. Первые комбинаторные задачи появились в трудах философов и математиков Средневековья.

Попытаемся разобраться в аспектах этой области науки: каковы элементы, свойства, правила, методы и основное ее применение в нашей жизни? Конечно, всю область в одной статье невозможно охватить. Поэтому ниже будет представлено всё самое основное.

Что такое комбинаторика в математике

Суть этого термина дают книги прошлых лет: это раздел математики, занимающийся операциями со множеством элементов.

В младших классах задачи на эту тему решают на дополнительных кружках, а в школах с углубленным изучением математики на основных уроках. К тому же, задачи по комбинаторике включены в олимпиады всех уровней.

Основные понятия

Элемент – любой объект или явление, входящий в искомое множество.
Сочетание – подмножества, находящиеся в произвольном порядке в исходном множестве.
Перестановка – элементы во множестве находятся в строго определенном порядке.
Размещение – упорядоченные подмножества в исходном множестве.

Правило произведения

Является одним из основных правил при решении таких задач и звучит так:

При выборе элемента А из n способов и выборе элемента В из m способов верно утверждение, что выбрать пару А и В одновременно можно n*m способами.

Рассмотрим на конкретных примерах.

Задача №1.

В коробке лежит 2 мяча и 6 скакалок. Сколько существует способов достать 1 мяч и 1 скакалку?

Ответ прост: 2 * 6 = 12.

Задача №2.

Есть 1 кубик, 2 шарика, 3 цветка и 4 конфеты. Сколькими способами можно вытянуть кубик, шарик, цветок и конфету?

Решение аналогично: 1 * 2 * 3 * 4 = 24.

Причем левую часть можно записать гораздо проще: 4!

! в данном случае является не знаком препинания, а факториалом. С помощью него можно вычислить более сложные варианты и решать трудные задачи (существуют разные формулы, но об этом позже).

Задача №3.

Сколько двузначных чисел можно составить из 2 цифр?

Задача №4.

Сколько десятизначных чисел можно составить из 10 цифр?

Правило суммы

Тоже является базовым правилом комбинаторики.

Если А можно выбрать n раз, а В — m раз, то А или В можно выбрать (n + m) раз.

Задача №5.

В коробке лежат 5 красных, 3 желтых, 7 зеленых, 9 черных карандашей. Сколько есть способов вытащить 1 любой карандаш?

Ответ: 5 + 3 + 7 + 9 = 24.

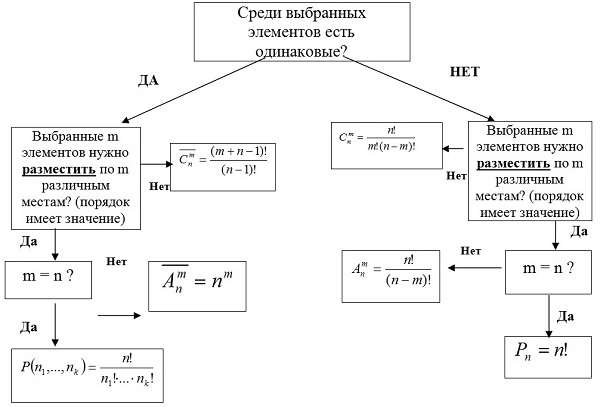
Сочетания с повторениями и без повторений

Под этим термином понимают комбинации в произвольном порядке из множества n по m элементов.

Число сочетаний равно количеству таких комбинаций.

Задача №6.

В коробке находится 4 разных фрукта. Сколькими способами можно достать одновременно 2 разных фрукта?

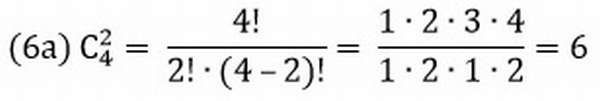
Где 4! – комбинация из 4 элементов.

С повторениями чуть сложней, комбинации считаются по такой формуле:

Задача №7.

Возьмем тот же самый случай, но при условии, что один фрукт возвращается в коробку.

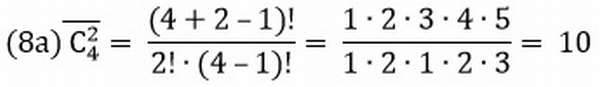
Размещения с повторениями и без повторений

Под этим определением понимают набор m элементов из множества n элементов.

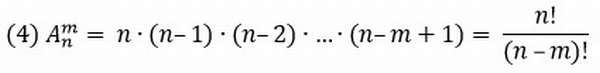
Задача №8.

Из 3 цифр надо выбрать 2, чтобы получались разные двузначные числа. Сколько вариантов?

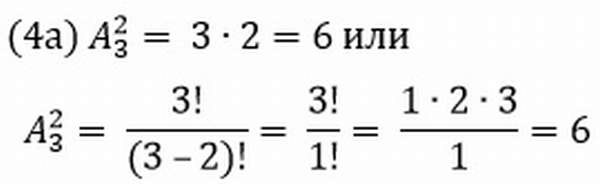
А как же быть с повторениями? Здесь каждый элемент может размещаться несколько раз! В таком случае общая формула будет выглядеть следующим образом:

Задача №9.

Из 12 букв латинского алфавита и 10 цифр натурального ряда надо найти все варианты составления автомобильного кода региона.

Перестановки с повторениями и без повторений

Под этим термином понимают все возможные комбинации из n элементного множества.

Задача №10.

Сколько возможных пятизначных чисел можно составить из 5цифр? А шестизначных из 6 цифр? Семизначных из 7 цифр?

Решения, согласно вышеприведенной формуле, следующие:

А как же быть с повторениями? Если в таком множестве есть одинаковые по своей значимости элементы, то перестановок будет меньше!

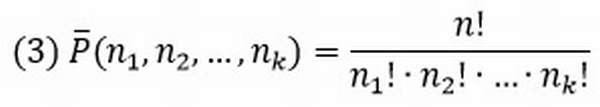
Задача №11.

В коробке есть 3 одинаковых карандаша и одна ручка. Сколько перестановок можно сделать?

Ответ прост: 4! / (3! * 1!) = 4.

Комбинаторные задачи с решениями

Примеры всех возможных типов задач с решениями были даны выше. Здесь попробуем разобраться с более сложными случаями, встречающимися в нашей жизни.

Типы задач	Что требуется найти	Методы решения
Магический квадрат	Фигура, в которой сумма чисел в рядах и столбцах должна быть одинакова (его разновидность – латинский квадрат).	Рекуррентные соотношения. Решается подобная же задача, но с гораздо меньшим множеством элементов по известным правилам и формулам.
Задача размещения	Стандартная производственная задача (например, в лоскутной технике) найти возможные способы разложения количества продуктов в ячейки в определенном порядке.	Включения и исключения. Как правило, применяется при доказательстве различных выражений.
Задачи про торговцев	Суть найти все возможные пути прохождения людей из пункта А в пункт В.	Траектории. Для этого вида задач характерно геометрическое построение возможных способов решения.

Заключение

Стоит изучать эту науку, поскольку в век быстрой модернизации технологий потребуются специалисты, способные предоставить различные решения тех или иных практических задач.

Читайте также: