Сообщение на тему история возникновения биссектрисы

Обновлено: 02.07.2024

После того как вы поделитесь материалом внизу появится ссылка для скачивания.

Подписи к слайдам:

Подготовка к олимпиадам

Несколько интересных фактов о биссектрисе

Дьёрдь Пойя

(венгерский, американский математик)

Разнообразить материал различными дополнительными сведениями.
Сделать выводы и дать рекомендации по использованию данного материала.

Несколько интересных фактов о биссектрисе

Биссектриса

Биссектри́са угла — луч с началом в вершине угла, делящий угол на два равных угла.

Биссектриса треугольника – отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны.

Несколько интересных фактов о биссектрисе

Биссектриса угла – геометрическое место точек, равноудалённых от сторон угла.

Если у какой-нибудь точки расстояния до сторон угла равны, то эта точка обязательно лежит на биссектрисе.

Выполняются сразу два утверждения:

Если точка лежит на биссектрисе, то расстояния от неё до сторон угла равны.

Несколько интересных фактов о биссектрисе

Биссектриса внутреннего угла перпендикулярна биссектрисе внешнего угла

Проверка домашней работы

1.114 (Гордин Р.К.)

Докажите, что биссектриса внешнего угла при вершине равнобедренного треугольника параллельна основанию. Верно ли обратное.

Проверка домашней работы

1. 145. (Гордин Р.К.) Найдите сумму пяти углов при вершинах пятиконечной звезды.

Проверка домашней работы

1.132. (Гордин Р.К.) Биссектриса внутреннего угла при вершине А и биссектриса внешнего угла при вершине С треугольника АВС пересекаются в точке М.

Проверка домашней работы

1.115. (Гордин Р.К.) Биссектрисы двух углов треугольника пересекаются под углом 1100. найдите третий угол треугольника.

Несколько интересных фактов о биссектрисе

Биссектрисы внутренних углов треугольника пересекаются в одной точке —инцентре — центре вписанной в этот треугольник окружности.

Несколько интересных фактов о биссектрисе

Центрами вневписанных окружностей являются точки пересечения биссектрис внешних углов треугольника.

Сколько вневписанных окружностей имеет треугольник?

Несколько интересных фактов о биссектрисе

Докажите, что точка D лежит на биссектрисе ВО.

Центр вписанной окружности в треугольник, вневписанной окружности и вершины треугольника (относительно одного угла) лежат на одной прямой.

Несколько интересных фактов о биссектрисе

Центр вневписанной окружности лежит на пересечении биссектрис внешнего и внутреннего угла треугольника (проведенных из вершин одной стороны)

Несколько интересных фактов о биссектрисе

Доказать: АМ, СК, BN высоты треугольника АВС.

Вершины остроугольного треугольника являются центрами вневписанных окружностей.

Основания высот треугольника образуют ортотреугольник

Несколько интересных фактов о биссектрисе

Вывод и анализ данного материала

Биссектриса внутреннего угла перпендикулярна биссектрисе внешнего угла

Центр вписанной окружности в треугольник, вневписанной окружности и вершины треугольника (относительно одного угла) лежат на одной прямой.

Основания высот треугольника образуют ортотреугольник

Несколько интересных фактов о биссектрисе

Существует ли треугольник, две биссектрисы которого перпендикулярны?

№ 1.135 (задача про кота);

По желанию: обратное утверждение 1.83

Несколько интересных фактов о биссектрисе

1.83. Докажите, что, если в треугольнике один угол равен 120◦, то треугольник, образованный основаниями его биссектрис, прямоугольный.

Проверка домашней работы

(VII олимпиада Эйлера, 2 тур)

Решение. Из условия следует, что ∠ABD = ∠EBD = ∠CEF = ∠DEF = ∠BDE. Таким образом, внутренние накрест лежащие углы ABD и BDE при пересечении прямой BD прямыми AB и DE равны. Следовательно, AB || DE, откуда ∠BAC = ∠EDF = ∠EDB = ∠ABD = ∠ABC/2, что и требовалось доказать.

В треугольнике ABC провели биссектрису BD, в треугольнике BDC — биссектрису DE, а в треугольнике DEC — биссектрису EF. Оказалось, что прямые BD и EF параллельны. Докажите, что угол ABC вдвое больше угла BAC.

Форма урока: семинар

объяснительно –иллюстративный;
проблемный;
исследовательский;

Технология применения ИКТ;
Проблемное обучение;
Профильное обучение;
Технология дифференцированного обучения;

организационный;
постановка цели и задач;
актуализация знаний;
введение знаний (;
подведение первичного закрепления;
подведение итогов ;
определение домашнего задания и инструктаж по его выполнению.

Для школьника проектно-исследовательская деятельность - это возможность раскрыть свои творческие способности. Это позволяет проявить себя индивидуально.

Проектно-исследовательская работа

Тема: Биссектриса знакомая и не очень

Выполнил: Лавринов Никита,

ученик 7 класса

Руководитель: Сотникова И.А.,

1. Определение и построение биссектрисы угла 4

2. Определение биссектрисы угла треугольника и замечательное свойство биссектрис треугольника 6

3. Занимательная информация о биссектрисе 9

Казалось бы, что такое биссектриса угла – знает каждый. Что тут сложного? Однако, просто знать – это одно, а вот использовать знание, применять его в деле – это другое. На уроках геометрии мы говорили о биссектрисе угла, биссектрисе угла треугольника и замечательном свойстве биссектрис треугольника.

Актуальность данной работы определяется тем, что биссектриса угла, биссектриса угла треугольника - это геометрические понятия, знания которых имеют огромное значение для решения задач, в том числе и заданий единого государственного экзамена.

Целью моей работы: показать замечательное свойство биссектрис треугольника с помощью построений циркуля и линейки.

Для достижения поставленной цели необходимо решить следующие задачи:

1. Изучить теоретический материал учебника и дополнительных источников информации и дать определение биссектрисы угла, биссектрисы треугольника.

2. Выяснить, каким замечательным свойством обладают биссектрисы углов треугольника.

3. Выполнить построения с помощью циркуля и линейки.

Объект исследования: биссектриса угла и биссектриса угла треугольника.

Предмет исследования: замечательное свойство биссектрис треугольника.

Определение и построение биссектрисы угла

Биссектриса - это место равноудаленных точек сторон угла. В более простых терминах биссектриса представляет собой линию, которая делит угол пополам.

Биссектриса - луч, выходящий из верхней части угла и разделяющий его на два других равных угла.

Как построить биссектрису угла с помощью циркуля?

Задан угол с вершиной в точке А, биссектрису которого нужно построить. Данный угол выходит из вершины А.

Ставим циркуль в точку A и проводим окружность любого радиуса R. Заданный угол пересечется с начерченной окружностью в двух точках. Назовем их В и С.

Чертим еще две окружности такого же радиуса с центрами в точках В и С. При пересечении этих двух начерченных окружностей получаем точку, которую назовем буквой D.

С помощью линейки из точки А через точку D проводим луч. Полученный луч и будет биссектрисой заданного угла А.

Есть несколько правил, которые могут помочь Вам найти биссектрису. К примеру:

— биссектриса делит противоположную сторону треугольника в таком отношении, которое равно отношению двух остальных сторон;

— две биссектрисы углов при основании равнобедренного треугольника равны;

— все три биссектрисы любого треугольника пересекутся в центре вписанной в этот треугольник окружности (эти утверждения мы докажем в 8 классе).

Я построил с помощью циркуля и линейки биссектрису угла по данному алгоритму.(см Приложение №1)

Также можно построить биссектрису с помощью транспортира.
Например, если Вам нужно построить биссектрису угла, равного 78 градусов, то нужно приложить транспортир к одной из сторон этого угла, отметить точку возле метки 78 / 2 = 39 градусов и провести луч из вершины заданного угла через полученную точку. Это и будет биссектриса угла 78 градусов. (см Приложение №2)

Определение биссектрисы угла треугольника и

замечательное свойство биссектрис треугольника

В дополнение к биссектрисе угла имеется также биссектриса треугольника, поскольку треугольник содержит до трех углов, так что каждый треугольник может иметь три разных биссектрисы. Что такое биссектриса треугольника?

Биссектриса треугольника является отрезком биссектрисы угла, соединяющего его вершину с точкой на противоположной стороне треугольника.

Треугольник и его построения имеют важное значение в начальной геометрии. Одно из построений треугольника – биссектриса - представляет собой прямой отрезок, исходящий из одной вершины треугольника и соединяющийся с точкой на противолежащем ребре. При этом биссектриса делит пополам угол данной вершины. В общем случае построение биссектрисы треугольника сводится к проведению биссектрисы угла конкретной вершины. Это построение можно выполнить с помощью транспортира, с помощью циркуля и линейки. Однако построение биссектрисы равнобедренного и правильного треугольников можно провести с учетом их геометрических свойств без дополнительных инструментов.

Постройте заданный треугольник. Возьмите транспортир и измерьте угол вершины, из которой необходимо провести биссектрису. Поделите данный угол пополам.

Отмерьте от стороны треугольника, прилегающей к данной вершине, высчитанный угол. Поставьте точку, обозначающую половину угла вершины.

Проведите через вершину и отмеченную точку прямую линию так, чтобы она ограничивалась вершиной с одной стороны и противолежащей стороной треугольника с другой. Биссектриса треугольника построена.

Если заданный треугольник является равнобедренным или правильным, то есть у него равные две или три стороны, то его биссектриса, согласно свойству треугольника, будет являться также и медианой. А, следовательно, противолежащая сторона будет делиться биссектрисой пополам.

Измерьте линейкой противолежащую строну треугольника, куда будет стремиться биссектриса. Поделите данную строну пополам и поставьте в середине стороны точку.

Проведите прямую линию, проходящую через построенную точку и противолежащую вершину. Это и будет биссектриса треугольника.

Построив биссектрисы углов остроугольного, тупоугольного и прямоугольного треугольников увидел, что биссектрисы треугольников пересеклись в одной точке. Интересно, а как это доказать? Об этом я и мои одноклассники узнаем на уроках геометрии в 8 классе.

3. Занимательная информация о биссектрисе

Мнемоническое (Мнемо́ника - греч. τα μνημονιχα — искусство запоминания), правило:

Биссектриса - это крыса, которая бегает по углам и делит угол пополам. (См Приложение№4).

Также есть много стихотворений, сказок и рассказов о биссектрисе, вот некоторые из них.

Стихотворение: Биссектриса

В углу у кипариса, фактически, в тени,
влачила Биссектриса безрадостные дни.
- Ах, я иного круга! Я не халам-балам!
На что мне этот угол, деленный пополам?

Сумела исхитриться на дерзкие дела,
сбежала Биссектриса, осталась без угла.
Но долетели сплетни, что, якобы, она
в окружности соседней Диаметру жена.

Живет с улыбкой гордой в нездешней стороне.
Теперь зовется Хордой и счастлива вполне.
А я сижу, не евши, вдали от Биссектрис,
в углу осиротевшем несчастный кипарис.

Пью чай из барбариса, а сердце – просто хлам! -
разбито Биссектрисой, как угол, пополам.
Все будто бы в тумане и тенькает висок.
Схожу-ка к Медиане – развеюсь на часок!

2. Биссектриса.

Заспорили Стороны угла, никак между собой не поладят.

— Я, со своей стороны, считаю… — говорит одна Сторона.

— А я считаю, со своей стороны… — возражает ей другая.

Ничего не поделаешь: хоть у них и общий угол зрения, но смотрят-то они на мир с разных сторон!

Проходила как-то между ними Биссектриса. Обрадовались Стороны: вот кто будет их посредником! Спрашивают Биссектрису:

— А вы как думаете?

— А ваше мнение каково?

Стоит посредник посрединке, колеблется.

— Ну, скажите же, скажите! — тормошат Биссектрису со всех сторон.

— Я думаю, вы совершенно правы, — наконец произносит Биссектриса, кивая в правую сторону.

— Ах, какая вы умница! — восхищается правая Сторона. — Как вы сразу все поняли!

А Биссектриса между тем поворачивается к левой Стороне:

— Ваша правда, я тоже всегда так думала.

Левая Сторона в восторге:

— Вот что значит Биссектриса! Сразу сообразила, что к чему!

Стоит Биссектриса и знай, раскланивается: в одну сторону кивнет — мол, правильно, в другую сторону кивнет — мол, совершенно верно. Мнение Биссектрисы ценится очень высоко, поскольку оно устраивает обе стороны.

Свою работу я начал с рассмотрения множества пособий по математике, использовал сеть Интернет. Из них я выбрал нужную информацию, изучил теорию. При изучении материала по этой теме, узнал очень много нового. В своей работе я выполнил построения биссектрисы угла с помощью циркуля и линейки, а также с помощью транспортира. И доказал с помощью построений замечательное свойство биссектрис углов треугольника.

Это понятие широко применяется в геометрии. И каждый школьник в России знакомится с ним уже в 5 классе. А после эта величина часто используется для решения различных задач.

Биссектриса — это.

Биссектриса – это луч, который выходит из вершины треугольника и делит ее ровно на две части.

Также под биссектрисой принято понимать и длину отрезка (что это?), который начинается в вершине треугольника, а заканчивается на противоположной от этой вершины стороне.

Пересечение биссектрис треугольника

Как можно было заметить по приведенным выше рисункам, у биссектрис треугольника есть одно важное свойство. А именно:

Биссектрисы треугольника всегда пересекаются в одной точке, называемой инцентром!

Это правило является аксиомой (что это такое?) и не допускает никаких исключений. Другими словами, вот такого быть не может:

Если вы видите такую картину, то перед вами точно не БИССЕКТРИСЫ. Во всяком случае, минимум один отрезок таковой не является. А может и все три.

А есть еще один интересный факт, связанный с пересечением биссектрис треугольника.

Центр пересечения биссектрис в треугольнике является центром окружности, который списан в эту фигуру.

Это свойство биссектрис на самом деле не только выглядит интересно на чертежах. Оно часто помогает в решение сложных задач.

Эта статья относится к рубрикам:

Комментарии и отзывы (3)

«Высота – линия, которая выходит из вершины треугольника и опускается на противоположную сторону под прямым углом.

Некорректно, линия бывает разная,а речь здесь идет о прямой, или её порождениях: отрезок и луч.

Математика требует точности. Спасибо.

При ознакомлении с таким теоретическим материалом всегда возникает вопрос, как можно использовать знания о биссектрисе в реальной жизни, за пределами учебного заведения.

Необходимость делать уроки с собственным ребенком в счет не идет. Конечно, такая информация повышает общую эрудицию, но не несет никакой практической нагрузки, а потому надолго не задерживается в памяти.

Никогда не был силен в геометрии, но наука эта очень важна, знаю, потому как не раз приходилось подтягивать свои знания для решения практических задач.

Сюрпризы биссектрисы треугольника

Автор работы награжден дипломом победителя II степени

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке "Файлы работы" в формате PDF

Актуальность исследования заключается в том, что на экзаменах по геометрии предлагаются задачи, для решения которых надо знать и уметь применить свойства, о которых в школьных учебниках даже не упоминается, но они значительно упрощают решение.

Для решения этой проблемы были рассмотрены некоторые малоизвестные, но очень важные свойства биссектрисы треугольника.

Объект исследования: биссектриса треугольника.

Предмет исследования: малоизвестные свойства биссектрисы треугольника.

Методы исследования: анализ учебников и справочной математической литературы; построения с помощью циркуля и линейки; компьютерное моделирование математических объектов с помощью ИГС GeoGebra; анализ, сравнение, сопоставление и обобщение объектов, полученных в результате моделирования; обобщение найденных с помощью компьютерного моделирования закономерностей; проверка выдвинутых гипотез; аналитические рассуждения.

Гипотеза: выполнив работу, будут найдены свойства биссектрисы угла треугольника, которые помогут решать задачи.

Цель работы – установление свойств биссектрисы угла треугольника, которые не изучаются в школе, но применяются при решении задач по геометрии и облегчают их решение.

Задачи исследования:

провести анализ информации о свойствах биссектрисы треугольника из различных источников информации;

обобщить свойства биссектрисы угла и биссектрисы угла треугольника, которые изучаются в школьном курсе геометрии;

привести примеры их применения при решении задач по математике;

привести пример задачи, для решения которой недостаточно знать известные со школьного курса геометрии свойства и приводящей к новому, неизвестному свойству биссектрисы угла треугольника;

доказать это неизвестное свойство биссектрисы угла треугольника – лемму о дважды биссектрисе;

исследовать лемму о дважды биссектрисе для остроугольных, прямоугольных и тупоугольных треугольников;

найти и решить задачи на применение леммы о дважды биссектрисе треугольника;

установить наличие других малоизвестных свойств биссектрисы треугольника.

ГЛАВА 1. СЮРПРИЗЫ БИССЕКТРИСЫ ТРЕУГОЛЬНИКА

1.1 Некоторые предварительные замечания. Линии в треугольнике

1) Медиана – отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

2) Биссектриса – отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противоположной стороне этого треугольника.

3) Средняя линия – отрезок, параллельный одной из его сторон и проходящий через середины сторон.

) Высота – перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону [2].

1.2 Свойства биссектрисы треугольника в школьных учебниках геометрии

В школьных учебниках геометрии описываются следующие свойства биссектрисы треугольника [2].

Все биссектрисы треугольника пересекаются в одной точке.

В равнобедренном треугольнике биссектриса угла при его вершине является и медианой, и высотой.

Биссектриса делит противоположную сторону на части, пропорциональные прилегающим сторонам: .

Биссектриса делит площадь треугольника пропорционально прилежащим сторонам.

Точка пересечения биссектрис является центром окружности, вписанной в этот треугольник.

Это был первый неожиданный для меня сюрприз биссектрисы угла треугольника!

Особое внимание обратил на задачу, в которой говорится об интересном свойстве биссектрисы угла треугольника, которое стало вторым сюрпризом биссектрисы треугольника (ПРИЛОЖЕНИЕ 1. Свойство о медиане, биссектрисе и высоте треугольника, проведенных из одной вершины).

1.3 От задачи к гипотезе

Задача. В остроугольном ∆АВС из вершины С проведены высота, биссектриса и отрезок, проходящий через центр описанной окружности до пересечения с противоположной стороной. Углы А и В равны соответственно 68˚и 34˚. Сравнить углы HCL, LCM и HCM и сформулировать гипотезу.

Δ ACB ‒ ∠ C = 180˚ ‒ (∠ A + ∠ B ) = 78˚;

ΔACH , ∠ H = 90˚, ∠ A = 68˚; ∠ ACH = ∠ H ‒ ∠ A = 22˚;

Δ ACL , CL – биссектриса ∠ ACB , ∠ ACL = = 39˚.

∠ HCL = ∠ ACL ‒ ∠ ACH = 39˚ ‒ 22˚ = 17˚.

∠ COB – центральный угол, ∠ CAB – вписанный угол, которые опираются на одну и ту же дугу. ∠ COB = 2∠ CAB = 68˚ × 2 = 136˚, ΔCOB – равнобедренный, ∠ OCB = = 22˚.

∠ LCM = ∠ LCB ‒ ∠ MCB = 39˚ ‒ 22˚ = 17˚.

Значит, CL – биссектриса ∠ HCM , то есть угла, стороны которого являются высотой и отрезком, проходящим через центр описанной окружности, проведенные из той же вершины данного треугольника.

Назовем эту гипотезу леммой о дважды биссектрисе в треугольнике.

1.4 Исследование леммы о дважды биссектрисе в остроугольном, прямоугольном и тупоугольном треугольниках

В ИГС Geogebra было выполнено моделирование леммы о дважды биссектрисе в остроугольном, прямоугольном и тупоугольном треугольниках и проведено исследование, в результате которого было установлено, что ∠ OAL = ∠ LAH в любом виде треугольника.

Вывод. На основании этих наблюдений можно сделать вывод о том, что лемма о дважды биссектрисе работает в любом треугольнике и в любом угле треугольника.

1.5 Лемма о дважды биссектрисе

Г ипотеза. Биссектриса AL остроугольного неравнобедренного ∆АВС является также биссектрисой угла ОАН, где O – центр окружности, описанной около треугольника АВС, АН – его высота.

Базовым понятием и одним из наиболее интересных и полезных объектов школьной математики является биссектриса. С её помощью доказываются многие положения планиметрии, упрощается решение задач.

Известные свойства позволяют рассматривать геометрические фигуры с разных точек зрения. Появляется вариативность при выборе пути доказательств.

Становится возможным использование инструмента алгебры, например, свойство пропорции, нахождение неизвестных величин, решение алгебраических уравнений при рассмотрении геометрических вопросов.

Что такое биссектриса в геометрии

Рассматривают луч, выходящий из вершины угла или его часть (отрезок), который делит угол пополам. Такой луч (или, соответственно, отрезок) называется биссектрисой.

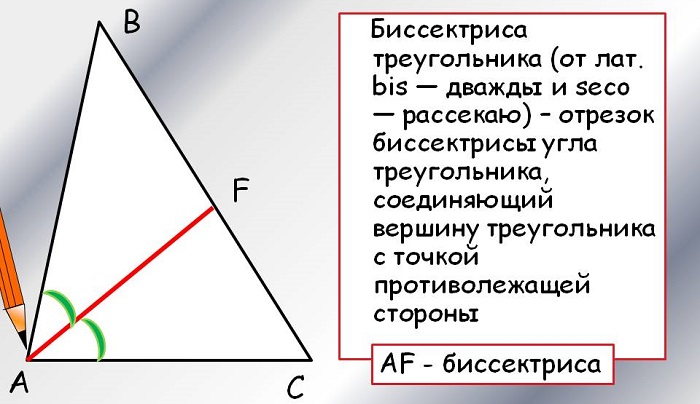
Часто для треугольников определение немного сужают, говоря об отрезке, соединяющем вершину угла, делящем его пополам, с точкой на противолежащей стороне. При этом рассматривается внутренняя область фигуры.

В то же время, часто при решении задач используются прямые, делящие внешние углы на два равных.

Биссектриса прямоугольного треугольника

Для прямоугольного треугольника одна из биссектрис образует равные углы, величины которых хорошо просчитываются (45 градусов).

Это помогает вычислять углы при решении задач, связанных с фигурами, которые можно представить в виде прямоугольных треугольников или прямоугольников.

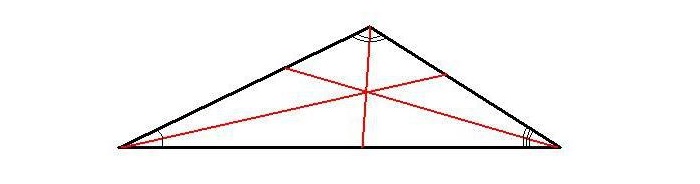
В тупоугольном треугольнике биссектриса делит больший угол на равные части, величина которых меньше 90 0 .

Свойства биссектрисы треугольника

1. Каждая точка этой линии равноудалена от сторон угла. Часто эту характеристику выбирают в качестве определения, поскольку верно и обратное утверждение для любого произвольного треугольника. Это позволяет находить и радиус вписанной окружности.

2. Все внутренние отрезки, делящие углы пополам, пересекаются в одной точке, которая является центром окружности, вписанной в фигуру, т. е. точка пересечения находится на равных расстояниях от сторон.

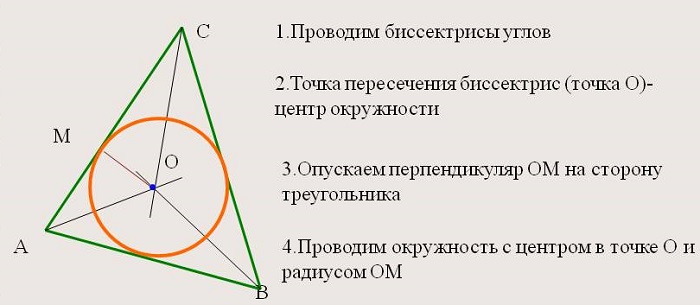
Данное свойство позволяет решать целый класс разнообразных задач, выводить формулы для радиусов вписанных окружностей правильных многоугольников.

Благодаря этому утверждению, легко доказывается следующее правило:

Площадь описанного многоугольника равна:

где p – полупериметр, а r – радиус вписанной окружности.

Это позволяет находить решение не только планиметрических, но и стереометрических задач.

Важную роль играют внешние биссектрисы треугольника. Вместе с внутренними они образуют прямые углы;

3. Сумма величин двух прилежащих сторон, делённая на длину противолежащей стороны, задаёт отношение частей биссектрисы (считая от вершины), полученных точкой пересечения всех трёх соответствующих линий.

Некоторые виды геометрических фигур, в силу своих особенностей, порождают особые примечательные характеристики;

4. В равнобедренном треугольнике биссектриса, проведённая к основанию, одновременно является медианой и высотой. Две другие – равны между собой.

В этом случае основание параллельно внешней биссектрисе.

Обратное положение также имеет место. Если прямая проведена параллельно основанию равнобедренного треугольника через некоторую вершину, то внешняя биссектриса при этой вершине является частью этой линии;

5. Для равностороннего многоугольника важной характеристикой считается равенство всех биссектрис;

6. У правильного треугольника все внешние биссектрисы параллельны сторонам;

7. Выделяют несколько особенностей, среди которых есть следующая теорема:

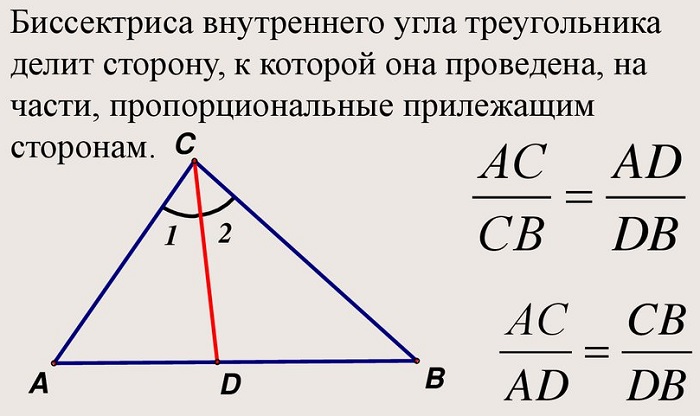
8. Разносторонний треугольник позволяет определить взаимное расположение его высоты, медианы и биссектрисы, проведённых из одной точки. В частности, медиана и высота располагаются по разные стороны от третьей линии.

Все формулы биссектрисы в треугольнике

В зависимости от исходных данных, длина биссектрисы, проведённой к стороне C, l_c, равна:

Примеры решения задач

Задача №1

В ΔABC ∠C = 90°, проведена биссектриса острого угла. Отрезок, соединяющий её основание с точкой пересечения медиан, перпендикулярен катету. Найти углы заданной фигуры.

Пусть ∠ACB = 90°, AD – биссектриса, BE – медиана, O – точка пересечения медиан, OD⊥BC.

Тогда OE : OB = 1 : 2по свойству медиан.

Так как OD⊥BC, то ODIIOC, следовательно, ΔBOD ∼ ΔBEC по второму признаку подобия, поэтому, по свойству подобных фигур, CD : DB = 1 : 2.

Это означает, что CA : AB = 1 : 2.

Так как катет равен половине гипотенузы, то ∠ABC = 30°, откуда ∠CAB = 60°.

Задача №2

Диагональ параллелограмма делит его острый угол пополам. Доказать, что этот параллелограмм является ромбом.

Доказательство.

Так как ABCD – параллелограмм, то ∠DAC = ∠ACB, как накрест лежащие при параллельных прямых AD, BC и секущей AC.

По условию, ∠DAC = ∠ACB = ∠BAC, поэтому ΔACB равнобедренный, то есть AB = BC, следовательно, ABCD – ромб.

Читайте также: