Понятие алгоритмических перечислений элементов конечного множества сообщение

Обновлено: 05.07.2024

В этой книге алгоритмы обсуждаются в разных главах и в двух различных аспектах. Первый аспект — теоретический, и его обсуж дению посвящен данный раздел, а второй — прагматический, тесно связанный с программированием, и излагается в седьмой главе.

Под алгоритмом всегда (и до возникновения строгой теории) понималась процедура, которая позволяла путем выполнения после довательности элементарных шагов получать однозначный результат (независящий от того, кто именно выполнял эти шаги) или за конечное число шагов прийти к выводу о том, что решения не существует.

Конечно же это нестрогое определение понятия алгоритма и именно попытки сформулировать такое понятие привели к возник новению теории алгоритмов. Причиной развития этой теории были внутренние проблемы математики и лишь с возникновением и развитием вычислительной техники и 'смежных наук выяснилось, что в основе этих наук должна лежать теория алгоритмов. Так стало очевидным прикладное значение новой науки.

чтобы выделить действительно необходимые элементы и свойства алгоритма и облегчить доказательства общих утверждений об этих свойствах. Универсальность необходима для того, чтобы модель позволяла описать любой алгоритм.

Результатами теоретических исследований явились три основных класса арифметических моделей.

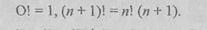
Другие примеры рекурсивной функции можно найти в разделе 7,2.

Второй класс моделей порожден следующей идеей. Для того чтобы алгоритм понимался однозначно, а его каждый шаг считался элементарным и выполнимым, он должен быть представлен так, чтобы его могла выполнять машина, к которой предъявляются уже упомянутые требования простоты и универсальности. Одной из таких машин явилась абстрактная машина Тьюринга. Машина Тьюринга

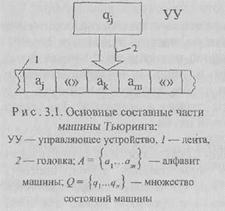состоит из трех частей (рис. 3.1): ленты, головки и управляющего устройства (УУ). Лента беско нечна в обе стороны и разбита на ячейки. В каждой ячейке может быть записан только один символ.

перемещаться вдоль ленты. Число возможных символов конечно, и образуют алфавит машины Л=<

Устройство управления хранит и выполняет команды машины вида qjOt -> qfl\d_p.

Конкретную машину Тьюринга (и алгоритм соответственно) можно задать, перечислив элементы AttQn команды машины.

Перед началом работы на пустую ленту записывается исходное слово а конечной длины, головка устанавливается над первым его символом и, как следствие, начальной конфигурацией является q\a.

Третий класс моделей алгоритмов очень близок к предыдущему,
но не оперирует конкретными машинными механизмами. Наиболее
известная алгоритмическая модель этого типа нормальные

Для нормального алгоритма задается алфавит, над которым он работает, конечное множество допустимых подстановок и порядок их применения. Если в качестве алфавита взять алфавит русского языка, а в качестве множества подстановок

то, используя правила 1—J:

1) проверить возможность подстановок в порядке возрастания их
номеров, и если она возможна (левая часть подстановки обнаружена в
исходном слове), произвести подстановку (заменив левую часть на
правую);

3) если ни одна подстановка не применима, то процесс преобра
зования завершен,

В теории алгоритмов строго доказано, что по своим возмож ностям преобразования нормальные алгоритмы эквивалентны машине Тьюринга и другим моделям, уточняющим понятия алго ритма.

Появление точного понятия алгоритма позволило сформу лировать алгоритмически не разрешимые проблемы, т.е. задачи, для решения которых невозможно построить алгоритм. Задача назы вается алгоритмически неразрешимой, если не существует машины Тьюринга (или рекурсивной функции, или нормального алгоритма Маркова), которая ее решает. Например, неразрешимой оказалась проблема распознавания эквивалентности алгоритмов: нельзя постро ить алгоритм, который по любым двум алгоритмам (программам) выяснял бы, вычисляют они одну и ту же функцию или нет. Знание основных неразрешимостей теории алгоритмов необходимо для специалиста по информатике. Оно предостережет его от увлечения глобальными прожектами всеобщей алгоритмизации точно так же, как знание основных законов физики предостерегает от попыток создания вечного двигателя.

Результатами теоретических исследований явились три основных класса арифметических моделей.

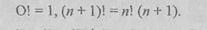
Другие примеры рекурсивной функции можно найти в разделе 7,2.

перемещаться вдоль ленты. Число возможных символов конечно, и образуют алфавит машины Л=< qfl\d_p.

то, используя правила 1—J:

3) если ни одна подстановка не применима, то процесс преобра
зования завершен,

Для учеников 1-11 классов и дошкольников
Бесплатные сертификаты учителям и участникам

МИНИСТЕРСТВО ОБРАЗОВАНИЯ ОРЕНБУРГСКОЙ ОБЛАСТИ

ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

РАБОЧАЯ ПРОГРАММА УЧЕБНОЙ ДИСЦИПЛИНЫ

для специальности

СОГЛАСОВАНО

Заместитель директора по МР

_____________________ А. А. Мязина

заседанием отделения программирования

Заведующий отделением программирования ___________________ Л.Н. Шапуленкова

на предметно-цикловой комиссии общеобразовательных и общепрофессиональных дисциплин

Председатель предметно-цикловой комиссии общеобразовательных и общепрофессиональных дисциплин ______________________Трушина И.Ю.

1.1. Область применения рабочей программы

1.2. Место учебной дисциплины в программе подготовки специалистов среднего звена

1.3. Цели и задачи учебной дисциплины - требования к результатам освоения учебной дисциплины:

Цель преподавания дисциплины: усвоение студентами теоретических основ дискретной математики и математической логики, составляющих фундамент ряда математических дисциплин и дисциплин прикладного характера.

Основные задачи курса :

- обеспечить обучающихся необходимыми теоретическим знаниями курса дискретной математики;

- овладение методами решения практических задач;

- приобретение навыков самостоятельной научной деятельности.

В результате освоения учебной дисциплины обучающийся должен уметь:

применять логические операции, формулы логики, законы алгебры логики;

выполнять операции над множествами; применять методы криптографической защиты информации; строить графы по исходным данным.

В результате освоения учебной дисциплины обучающийся должен знать:

иметь понятия функции алгебры логики;

представление функции в совершенных нормальных формах, многочлен Жегалкина; основные классы функций, полноту множества функций, теорему Поста;

основные понятия теории множеств;

логику предикатов, бинарные отношения и их виды;

элементы теории отображений и алгебры подстановок;

основы алгебры вычетов и их приложение к простейшим криптографическим шифрам;

метод математической индукции; алгоритмическое перечисление основных комбинаторных объектов;

основные понятия теории графов, характеристики графов, Эйлеровы и Гамильтоновы графы, плоские графы, деревья, ориентированные графы, бинарные деревья;

элементы теории автоматов.

Часы из вариативной части в количестве 68 были добавлены на углубленное изучение и практические занятия следующих разделов через введение новых дидактических единиц:

Раздел 1. Логика высказываний ( Операции над высказываниями. Основные принципы математической логики. Равносильность логических формул. Формулы алгебры высказываний. Упрощения формул логики с помощью равносильных преобразований. ) – 6 часов.

Раздел 2. Предикаты. Кванторы (Основы языка и алгебры предикатов. Формализация предложений с помощью логики предикатов; определение логического значения высказываний с кванторами. Понятие предикатной формулы; свободные и связанные переменные. Построение отрицаний к предикатам, содержащим кванторные операции ) – 4 часа.

Раздел 3. Булевы функции ( Виды и свойства булевых функций. Представление булевой функции в виде совершенной ДНФ, совершенной КНФ. Представление булевой функции в виде минимальной ДНФ. Методы минимизации алгебраических преобразований. Преобразование булевых функций помощью равносильных преобразований. Представление булевых функций в виде многочлена Жегалкина. Проверка множества булевых функций на полноту. Представление булевых функций в виде многочлена Жегалкина. Проверка множества булевых функций на полноту)- 12 часов.

Раздел 4. Основы теории множеств (Основные принципы теории множеств. Решение задач на выполнение теоретико-множественных операций )-4 часа.

Раздел 5. Бинарные отношения ( Понятие бинарного отношения и их видов; примеры бинарных отношений. Диаграмма бинарного отношения. Понятия рефлексивного, симметричного, транзитивного бинарного отношения. Отношение эквивалентности; теорема о разбиении множества на классы эквивалентности. Элементы теории отображений. Взаимооднозначные (биективные) отображения. Операция композиции отображений и её свойства. Диаграмма внутреннего отображения, заданного на конечном множестве; циклы. Элементы алгебры подстановок . Формула количества подстановок. Циклическое разложение подстановки. Произведение подстановок. Обратная подстановка. Методика решения простейших уравнений. Бинарные отношения и их свойства. Отношения эквивалентности, отношения строгого и нестрогого порядков. Соответствия и отображения. Алгебра подстановок) - 12 часов.

Раздел 6. Простейшие криптографические шифры ( Проблема криптографической защиты информации; понятие шифрования. Шифры замены. Шифр Цезаря и шифр Виженера как частные случаи шифров замены. Перестановочные шифры. Основы алгебры вычетов и их приложение к простейшим криптографическим шифрам. Шифрование текстов различными способами )-6 часов.

Раздел 7. Метод математической индукции (Умозаключения как форма мышления. Дедуктивные умозаключения и их виды. Индуктивные умозаключения и их виды. Метод математической индукции. Принцип метода математической индукции. Некоторые разновидности (модификации) метода математической индукции. Применение метода математической индукции для доказательства утверждений) - 4 часа.

Раздел 8. Алгоритмическое перечисление основных комбинаторных объектов ( Алгоритмическое перечисление основных комбинаторных объектов. Понятие алгоритмического перечисления (генерирования) элементов конечного множества. Генерирование двоичных слов заданной длины. Генерирование элементов декартова произведения множеств. Генерирование перестановок заданной длины. Генерирование К-элементных подмножеств данного множества. Генерирование всех подмножеств данного множества. Генерирование комбинаторных объектов заданного типа. Элементы теории автоматов. Построение простейших автоматов ) - 4 часа.

Раздел 9. Основы теории графов (Методика выделения компонент связности в графе. Мосты и разделяющие вершины. Расстояние между вершинами в графе: определение, свойства, методика нахождения. Задачи, сводящиеся к графам. Расстояния и пути в графах. Элементы сетевого планирования. Критические пути, работы, резервы. Двудольные графы. Методика проверки графа на двудольность. Полный двудольный граф. Изоморфные графы. Методика проверки пары графов на изоморфность. Плоские графы. Эйлеровы и Гамильтоновы графы. Теоремы Эйлера. Методика нахождения эйлерова цикла в эйлеровом графе. Бинарные деревья и их свойства. Кодирование Пруфера для деревьев с пронумерованными вершинами. Определение типа графов и их характеристик. Распознавание мостов и разделяющих вершин. Нахождение расстояний между вершинами в графе. Исследование графов на заданные свойства; применение аппарата теории графов для решения прикладных задач ) - 10 часов.

Раздел 10. Элементы теории автоматов ( Основные принципы теории алгоритмов. Абстрактные исполнители и формальные системы вычислений. Нормальный алгоритм Маркова. Машина Тьюринга. Машина Поста.

Элементы теории автоматов. Базовые множества для автомата: входной алфавит, выходной алфавит, множества состояний. Таблица автомата. Словарная функция автомата. Правильный автомат. Общие задачи теории автоматов. Машина Поста. Тезис Чёрча — Тьюринга и алгоритмически неразрешимые проблемы ) - 4 часа.

Работодатель требует от выпускника данной специальности наличие более глубоких знаний, на что и отведены часы вариативной части: для решения задач сетевого администрирования необходимы знания теории графов; для описания связи релейно-контактных схем с формулами логики и их использование для описания функционирования автоматов необходимы знания математической логики.

Аппарат дискретной математики необходим при создании и эксплуатации современных ЭВМ, средств передачи и обработки информации, автоматизированных систем управления и проектирования; поэтому знание основ данной дисциплины абсолютно необходимо для современного специалиста в области информатики и вычислительной техники.

1.4. Требования к результатам освоения программы подготовки специалистов среднего звена

1.4.1. Сетевой и системный администратор должен обладать общими компетенциями :

ОК 1. Выбирать способы решения задач профессиональной деятельности, применительно к различным контекстам.

ОК 2. Осуществлять поиск, анализ и интерпретацию информации, необходимой для выполнения задач профессиональной деятельности.

ОК 4. Работать в коллективе и команде, эффективно взаимодействовать с коллегами, руководством, клиентами.

ОК 5. Осуществлять устную и письменную коммуникацию на государственном языке с учетом особенностей социального и культурного контекста.

ОК 9. Использовать информационные технологии в профессиональной деятельности

ОК 10. Пользоваться профессиональной документацией на государственном и иностранном языке.

1.5. Количество часов на освоение рабочей программы учебной дисциплины

Приветствую вас на первом уроке по высшей алгебре, который появился… в канун пятилетия сайта, после того, как я уже создал более 150 статей по математике, и мои материалы начали оформляться в завершённый курс. Впрочем, буду надеяться, что не опоздал – ведь многие студенты начинают вникать в лекции только к государственным экзаменам =)

Вузовский курс вышмата традиционно зиждется на трёх китах:

– математическом анализе (пределы, производные и т.д.)

Множество. Примеры множеств

Множество – это фундаментальное понятие не только математики, но и всего окружающего мира. Возьмите прямо сейчас в руку любой предмет. Вот вам и множество, состоящее из одного элемента.

В широком смысле, множество – это совокупность объектов (элементов), которые понимаются как единое целое (по тем или иным признакам, критериям или обстоятельствам). Причём, это не только материальные объекты, но и буквы, цифры, теоремы, мысли, эмоции и т.д.

Обычно множества обозначаются большими латинскими буквами (как вариант, с подстрочными индексами: и т.п.), а его элементы записываются в фигурных скобках, например:

– множество букв русского алфавита;
– множество натуральных чисел;

ну что же, пришла пора немного познакомиться:
– множество студентов в 1-м ряду

… я рад видеть ваши серьёзные и сосредоточенные лица =)

Множества и являются конечными (состоящими из конечного числа элементов), а множество – это пример бесконечного множества. Кроме того, в теории и на практике рассматривается так называемое пустое множество:

– множество, в котором нет ни одного элемента.

Пример вам хорошо известен – множество на экзамене частенько бывает пусто =)

Принадлежность элемента множеству записывается значком , например:

В абстрактной и не очень алгебре элементы множества обозначают маленькими латинскими буквами и, соответственно, факт принадлежности оформляется в следующем стиле:

– элемент принадлежит множеству .

Вышеприведённые множества записаны прямым перечислением элементов, но это не единственный способ. Многие множества удобно определять с помощью некоторого признака (ов), который присущ всем его элементам. Например:

– множество всех натуральных чисел, меньших ста.

Данное множество можно записать и прямым перечислением:

Ещё примеры:
– и если и студентов в 1-м ряду достаточно много, то такая запись намного удобнее, нежели их прямое перечисление.

– множество чисел, принадлежащих отрезку . Обратите внимание, что здесь подразумевается множество действительных чисел (о них позже), которые перечислить через запятую уже невозможно.

Подмножества

Практически всё понятно из самого названия: множество является подмножеством множества , если каждый элемент множества принадлежит множеству . Иными словами, множество содержится во множестве :

Значок называют значком включения.

Вернёмся к примеру, в котором – это множество букв русского алфавита. Обозначим через – множество его гласных букв. Тогда:

Также можно выделить подмножество согласных букв и вообще – произвольное подмножество, состоящее из любого количества случайно (или неслучайно) взятых кириллических букв. В частности, любая буква кириллицы является подмножеством множества .

Отношения между подмножествами удобно изображать с помощью условной геометрической схемы, которая называется кругами Эйлера.

Пусть – множество студентов в 1-м ряду, – множество студентов группы, – множество студентов университета. Тогда отношение включений можно изобразить следующим образом:

Множество студентов другого ВУЗа следует изобразить кругом, который не пересекает внешний круг; множество студентов страны – кругом, который содержит в себе оба этих круга, и т.д.

Типичный пример включений мы наблюдаем при рассмотрении числовых множеств. Повторим школьный материал, который важно держать на заметке и при изучении высшей математики:

Числовые множества

Как известно, исторически первыми появились натуральные числа, предназначенные для подсчёта материальных объектов (людей, кур, овец, монет и т.д.). Это множество уже встретилось в статье, единственное, мы сейчас чуть-чуть модифицируем его обозначение. Дело в том, что числовые множества принято обозначать жирными, стилизованными или утолщёнными буквами. Мне удобнее использовать жирный шрифт:

Иногда к множеству натуральных чисел относят ноль.

Если к множеству присоединить те же числа с противоположным знаком и ноль, то получится множество целых чисел:

Совершенно понятно, что множество натуральных чисел является подмножеством множества целых чисел:
– поскольку каждый элемент множества принадлежит множеству . Таким образом, любое натуральное число можно смело назвать и целым числом.

И, коль скоро, целые, то сразу же вспомним важные признаки их делимости на 2, 3, 4, 5 и 10, которые будут требоваться в практических вычислениях чуть ли не каждый день:

Целое число делится на 2 без остатка, если оно заканчивается на 0, 2, 4, 6 или 8 (т.е. любой чётной цифрой). Например, числа:
400, -1502, -24, 66996, 818 – делятся на 2 без остатка.

400 – делится на 4 (т.к. 00 (ноль) делится на 4);
-1502 – не делится на 4 (т.к. 02 (двойка) не делится на 4);
-24, понятно, делится на 4;
66996 – делится на 4 (т.к. 96 делится на 4);
818 – не делится на 4 (т.к. 18 не делится на 4).

Самостоятельно проведите несложное обоснование данного факта.

С делимость на 3 чуть сложнее: целое число делится на 3 без остатка, если сумма входящих в него цифр делится на 3.

Проверим, делится ли на 3 число 27901. Для этого просуммируем его цифры:
2 + 7 + 9 + 0 + 1 = 19 – не делится на 3
Вывод: 27901 не делится на 3.

Просуммируем цифры числа -825432:
8 + 2 + 5 + 4 + 3 + 2 = 24 – делится на 3
Вывод: число -825432 делится на 3

Целое число делится на 5, если оно заканчивается пятёркой либо нулём:
775, -2390 – делятся на 5

Целое число делится на 10, если оно заканчивается на ноль:
798400 – делится на 10 (и, очевидно, на 100). Ну и, наверное, все помнят – для того, чтобы разделить на 10, нужно просто убрать один ноль: 79840

Также существуют признаки делимости на 6, 8, 9, 11 и т.д., но практического толку от них практически никакого =)

Следует отметить, что перечисленные признаки (казалось бы, такие простые) строго доказываются в теории чисел. Этот раздел алгебры вообще достаточно интересен, однако его теоремы… прямо современная китайская казнь =) А Вольдемару за последней партой и того хватило…, но ничего страшного, скоро мы займёмся живительными физическими упражнениями =)

Следующим числовым множеством идёт множество рациональных чисел:
– то есть, любое рациональное число представимо в виде дроби с целым числителем и натуральным знаменателем.

Очевидно, что множество целых чисел является подмножеством множества рациональных чисел:

И в самом деле – ведь любое целое число можно представить в виде рациональной дроби , например: и т.д. Таким образом, целое число можно совершенно законно назвать и рациональным числом.

либо
– конечная десятичная дробь,

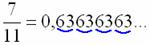
либо
– бесконечная периодическая десятичная дробь (повтор может начаться не сразу).

Полюбуйтесь делением и постарайтесь выполнять это действие как можно реже! В организационной статье Высшая математика для чайников и на других уроках я неоднократно повторял, повторяю, и буду повторять эту мантру:

В высшей математике все действия стремимся выполнять в обыкновенных (правильных и неправильных) дробях

Согласитесь, что иметь дело с дробью значительно удобнее, чем с десятичным числом 0,375 (не говоря уже о бесконечных дробях).

Объединение рациональных и иррациональных чисел образует множество действительных (вещественных) чисел:

– значок объединения множеств.

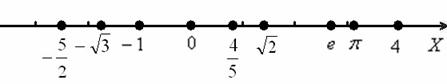
Геометрическая интерпретация множества вам хорошо знакома – это числовая прямая:

Каждому действительному числу соответствует определённая точка числовой прямой, и наоборот – каждой точке числовой прямой обязательно соответствует некоторое действительное число. По существу, сейчас я сформулировал свойство непрерывности действительных чисел, которое хоть и кажется очевидным, но строго доказывается в курсе математического анализа.

С вложениями всё прозрачно: множество рациональных чисел – это подмножество множества действительных чисел:
, таким образом, любое рациональное число можно смело назвать и действительным числом.

Множество иррациональных чисел – это тоже подмножество действительных чисел:

При этом подмножества и не пересекаются – то есть ни одно иррациональное число невозможно представить в виде рациональной дроби.

Существуют ли какие-нибудь другие числовые системы? Существуют! Это, например, комплексные числа, с которыми я рекомендую ознакомиться буквально в ближайшие дни или даже часы.

Ну а пока мы переходим к изучению операций над множествами, дух которых уже материализовался в конце этого параграфа:

Действия над множествами. Диаграммы Венна

Диаграммы Венна (по аналогии с кругами Эйлера) – это схематическое изображение действий с множествами. Опять же предупреждаю, что я рассмотрю не все операции:

1) Пересечение множеств характеризуется логической связкой И и обозначается значком

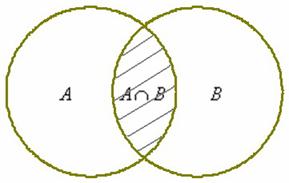
Пересечением множеств и называется множество , каждый элемент которого принадлежит и множеству , и множеству . Грубо говоря, пересечение – это общая часть множеств:

Так, например, для множеств :

Если у множеств нет одинаковых элементов, то их пересечение пусто. Такой пример нам только что встретился при рассмотрении числовых множеств:

Множества рациональных и иррациональных чисел можно схематически изобразить двумя непересекающимися кругами.

Операция пересечения применима и для бОльшего количества множеств, в частности в Википедии есть хороший пример пересечения множеств букв трёх алфавитов.

2) Объединение множеств характеризуется логической связкой ИЛИ и обозначается значком

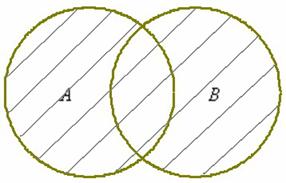
Объединением множеств и называется множество , каждый элемент которого принадлежит множеству или множеству :

Запишем объединение множеств :
– грубо говоря, тут нужно перечислить все элементы множеств и , причём одинаковые элементы (в данном случае единица на пересечении множеств) следует указать один раз.

Но множества, разумеется, могут и не пересекаться, как это имеет место быть с рациональными и иррациональными числами:

В этом случае можно изобразить два непересекающихся заштрихованных круга.

Операция объединения применима и для бОльшего количества множеств, например, если , то:

, при этом числа вовсе не обязательно располагать в порядке возрастания (это я сделал исключительно из эстетических соображений). Не мудрствуя лукаво, результат можно записать и так:

А вот эта разность оказывается пуста: . И в самом деле – если из множества натуральных чисел исключить целые числа, то, собственно, ничего и не останется :)

4) Декартовым (прямым) произведением множеств и называется множество всех упорядоченных пар , в которых элемент , а элемент

Но это чисто для удобства – и в том, и в другом случае пары можно перечислить в каком угодно порядке – здесь важно записать все возможные пары.

А теперь гвоздь программы: декартово произведение – это есть не что иное, как множество точек нашей родной декартовой системы координат .

Задание для самостоятельного закрепления материала:

Выполнить операции , если:

Множество удобно расписать перечислением его элементов.

И пунктик с промежутками действительных чисел:

Краткое решение задачи в конце урока.

Отображение множеств

Отображение множества во множество – это правило, по которому каждому элементу множества ставится в соответствие элемент (или элементы) множества . В том случае если в соответствие ставится единственный элемент, то данное правило называется однозначно определённой функцией или просто функцией.

Функцию, как многие знают, чаще всего обозначают буквой – она ставит в соответствие каждому элементу единственное значение , принадлежащее множеству .

Ну а сейчас я снова побеспокою множество студентов 1-го ряда и предложу им 6 тем для рефератов (множество ):

Установленное (добровольно или принудительно =)) правило ставит в соответствие каждому студенту множества единственную тему реферата множества .

…а вы, наверное, и представить себе не могли, что сыграете роль аргумента функции =) =)

Элементы множества образуют область определения функции (обозначается через ), а элементы множества – область значений функции (обозначается через ).

Построенное отображение множеств имеет очень важную характеристику: оно является взаимно-однозначным или биективным (биекцией). В данном примере это означает, что каждому студенту поставлена в соответствие одна уникальная тема реферата, и обратно – за каждой темой реферата закреплён один и только один студент.

Однако не следует думать, что всякое отображение биективно. Если на 1-й ряд (к множеству ) добавить 7-го студента, то взаимно-однозначное соответствие пропадёт – либо один из студентов останется без темы (отображения не будет вообще), либо какая-то тема достанется сразу двум студентам. Обратная ситуация: если к множеству добавить седьмую тему, то взаимнооднозначность отображения тоже будет утрачена – одна из тем останется невостребованной.

Итак, что же такое функция одной переменной? Функция одной переменной – это правило , которое каждому значению независимой переменной из области определения ставит в соответствие одно и только одно значение .

Задание 2: просмотреть графики основных элементарных функций и выписать на листок биективные функции. Список для сверки в конце этого урока.

Мощность множества

Интуиция подсказывает, что термин характеризует размер множества, а именно количество его элементов. И интуиция нас не обманывает!

Мощность пустого множества равна нулю.

Мощность множества равна шести.

Мощность множества букв русского алфавита равна тридцати трём.

И вообще – мощность любого конечного множества равно количеству элементов данного множества.

…возможно, не все до конца понимают, что такое конечное множество – если начать пересчитывать элементы этого множества, то рано или поздно счёт завершится. Что называется, и китайцы когда-нибудь закончатся.

Само собой, множества можно сравнивать по мощности и их равенство в этом смысле называется равномощностью. Равномощность определяется следующим образом:

Два множества являются равномощными, если между ними можно установить взаимно-однозначное соответствие.

Множество студентов равномощно множеству тем рефератов, множество букв русского алфавита равномощно любому множеству из 33 элементов и т.д. Заметьте, что именно любому множеству из 33 элементов – в данном случае имеет значение лишь их количество. Буквы русского алфавита можно сопоставить не только с множеством номеров
1, 2, 3, …, 32, 33, но и вообще со стадом в 33 коровы.

Примеров очень много. В частности, счётным является множество всех чётных натуральных чисел . Как это доказать? Нужно установить его взаимно-однозначное соответствие с множеством натуральных чисел или попросту пронумеровывать элементы:

Взаимно-однозначное соответствие установлено, следовательно, множества равномощны и множество счётно. Парадоксально, но с точки зрения мощности – чётных натуральных чисел столько же, сколько и натуральных!

Множество целых чисел тоже счётно. Его элементы можно занумеровать, например, так:

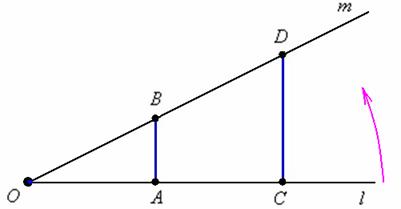
Поскольку между множеством и числовой прямой существует взаимно-однозначное соответствие (см. выше), то множество точек числовой прямой тоже несчётно. И более того, что на километровом, что на миллиметровом отрезке – точек столько же! Классический пример:

Поворачивая луч против часовой стрелки до его совмещения с лучом мы установим взаимно-однозначное соответствие между точками синих отрезков. Таким образом, на отрезке столько же точек, сколько и на отрезке и !

Данный парадокс, видимо, связан с загадкой бесконечности… но мы сейчас не будем забивать голову проблемами мироздания, ибо на очереди основы математической логики, а не философия =)

Спасибо за внимание и успехов вам в учёбе!

Задание 1

2)
– это множество нечётных натуральных чисел:

– все точки координатной плоскости , удовлетворяющие двум указанным неравенствам. Аналогично:

Задание 2 Взаимно-однозначные функции на иллюстрациях урока Функции и графики:

Автор: Емелин Александр

(Переход на главную страницу)

cкидкa 15% на первый зaкaз, при оформлении введите прoмoкoд: 5530-hihi5

Данная тема содержит немало терминологии, поэтому я добавлю содержание темы, которое позволит легче ориентироваться в материале.

Начнём с того, что же, собственно, понимать под словом "множество". На интуитивном уровне под множеством понимают некую совокупность объектов, именуемых элементами множества. Например, можно говорить о множестве груш на столе, множестве букв в слове "множество" и так далее. Георг Кантор (немецкий математик, основатель современной теории множеств) писал, что под "множеством я понимаю вообще всё то многое, которое возможно мыслить как единое, т.е. такую совокупность определённых элементов, которая посредством одного закона может быть соединена в одно целое". Некоторое время понятие множества, введённое Кантором, полагалось довольно очевидным и не требующим дополнительных пояснений. Казалось, что появление работ Больцано, а затем и Кантора в конце 19 - начале 20 века, положит конец многим вопросам (например, окончательно разрешит апории Зенона, разрешит проблему бесконечности и т.д.) и станет началом новой математики. Гениальный немецкий математик Давид Гильберт отмечал, что "Никто не изгонит нас из рая, созданного Кантором".

Однако появление парадоксов (Рассел, Бурали-Форти) положило конец "канторовскому раю". Одна из формулировок парадокса Рассела, известная под названием "парадокс брадобрея" звучит так: в некотором селе брадобрей бреет тех и только тех жителей села, которые не бреются сами. Кто же тогда бреет самого брадобрея? Допустим, он бреет себя самостоятельно. Т.е. он принадлежит к тем жителям села, которые бреются сами, – а ведь согласно условию этих жителей брадобрей не имеет права брить. Следовательно, допущение о том, что брадобрей бреется сам, приводит к противоречию. Попробуем иначе: пусть брадобрей не бреется сам. Если он сам не бреется, то согласно условию его обязан брить брадобрей – вновь противоречие! Были предприняты попытки разрешить противоречия теории множеств, предложенной Кантором. Саму канторовскую теорию множеств математики назвали "наивной". Целью многих математических трудов стало построение такой системы аксиом, в которой подобные парадоксы были бы невозможны. Но задача оказалась не столь уж проста. На данный момент, насколько мне известно, единой аксиоматики теории множеств нет. Наиболее распространенной считается система аксиом Цермело-Френкеля (ZFC), в которой особняком стоит так называемая "аксиома выбора". Есть и вариации этой системы: например, автор B-метода Жан-Раймонд Абриал предложил типизированную теорию множеств, на основании которой создал формальный метод разработки программ.

Обозначение множеств. Принадлежность элемента множеству. Пустое множество.

Обычно множества записываются в фигурных скобках. Например, множество всех гласных букв русского алфавита будет записано так:

А множество всех целых целых чисел, больших 8, но меньших 15, будет таким:

Множество может вообще не содержать ни одного элемента. В этом случае его именуют пустым множеством и обозначают как $\varnothing$.

Чаще всего в математической литературе множества обозначаются с помощью больших букв латинского алфавита. Например:

Есть и устоявшиеся обозначения определённых множеств. Например, множество натуральных чисел принято обозначать буквой $N$; множество целых чисел – буквой $Z$; множество рациональных чисел – буквой $Q$; множество всех действительных чисел – буквой $R$. Есть и иные устоявшиеся обозначения, но к ним мы станем обращаться по мере необходимости.

Множество, которое содержит конечное количество элементов, именуют конечным множеством. Если множество содержит бесконечное количество элементов, его называют бесконечным.

Например, указанное выше множество $A=\$ – конечное множество, ибо содержит 4 элемента (т.е. конечное число элементов). Множество натуральных чисел $N$ является бесконечным. Вообще говоря, мы не всегда можем сразу с уверенностью сказать, бесконечно некое множество или нет. Например, пусть $F$ – множество простых чисел.

Что такое простое число: показать\скрыть

Простыми числами именуют такие натуральные числа большие 1, которые делятся лишь на 1 или на самое себя. Например, 2, 3, 5, 7 и так далее. Для сравнения: число 12 не является простым числом, так как оно делится не только на 12 и 1, а ещё и на иные числа (например, на 3). Число 12 является составным.

Возникает вопрос: бесконечно множество $F$ или нет? Существует ли наибольшее простое число? Для ответа на этот вопрос понадобилась целая теорема, доказанная Эвклидом, о том, что множество простых чисел – бесконечно.

Под мощностью множества для конечных множеств понимают количество элементов данного множества. Мощность множества $A$ обозначается как $|A|$.

Например, так как конечное множество $A=\$ содержит 4 элемента, то мощность множества $A$ равна 4, т.е. $|A|=4$.

Если нам известно, что некий объект $a$ принадлежит множеству $A$, то записывают это так: $a\in A$. Например, для вышеуказанного множества $A$ можно записать, что $5\in A$, $-9\in A$. Если же объект $a$ не принадлежит множеству $A$, то обозначается это следующим образом: $a\notin A$. Например, $19\notin A$. Кстати, сказать, элементами множеств могут быть и иные множества, например:

Элементами множества $M$ являются числа -9, 1, 0, а также множество $ \< a,\; g\>$ и пустое множество $\varnothing$. Вообще, для упрощения восприятия множество можно представлять как портфель. Пустое множество – пустой портфель. Эта аналогия пригодится чуть далее.

Подмножество. Универсальное множество. Равенство множеств. Булеан.

Множество $A$ называют подмножеством множества $B$, если все элементы множества $A$ являются также элементами множества $B$. Обозначение: $A\subseteq B$.

Например, рассмотрим множества $K=\< -9,5\>$ и $T=\$. Каждый элемент множества $K$ (т.е. -9 и 5) является также элементом множества $T$. Следовательно, множество $K$ есть подмножество множества $T$, т.е. $K\subseteq T$.

Так как все элементы любого множества $A$ принадлежат самому множеству $A$, то множество $A$ является подмножеством самого множества $A$. Пустое множество $\varnothing$ является подможеством любого множества. Т.е. для произвольного множества $A$ верно следующее:

$$A\subseteq A; \; \varnothing\subseteq A.$$

Введём ещё одно определение – универсальное множество.

Универсальное множество (универсум) $U$ обладает тем свойством, что все иные множества, рассматриваемые в данной задаче, являются его подмножествами.

Иными словами, универсум содержит в себе элементы всех множеств, которые рассматриваются в рамках некоей задачи. Например, рассмотрим такую задачу: проводится опрос студентов некоей академгруппы. Каждому студенту предлагается указать мобильных операторов РФ, сим-карты которых он использует. Данные этого опроса можно представить в виде множеств. Например, если студент Василий использует сим-карты от МТС и Life, то можно записать следующее:

Подобные множества можно составить для каждого студента. Универсумом в этой модели будет множество, в котором перечислены все операторы России. В принципе, в качестве универсума можно взять также множество, в котором перечислены все операторы СНГ, а также множество всех мобильных операторов мира. И это не будет противоречием, ибо любой оператор России входит в множество операторов как СНГ, так и всего мира. Итак, универсум определяется только в рамках некоей конкретной задачи, при этом зачастую можно рассмотреть несколько универсальных множеств.

Множества $A$ и $B$ называются равными, если они состоят из одних и тех же элементов. Иными словами, если каждый элемент множества $A$ является также элементом множества $B$, и каждый элемент множества $B$ является также элементом множества $A$, то $A=B$.

Определение равенства множеств можно записать и по-иному: если $A\subseteq B$ и $B\subseteq A$, то $A=B$.

Рассмотрим пару множеств: первое будет $\$, а второе – $\$. Каждый элемент первого множества (т.е. $\Delta$ и $k$) является также элементом второго множества. Каждый элемент второго множества (т.е. $k$ и $\Delta$) является также элементом второго множества. Вывод: $\=\$. Как видите, порядок записи элементов в множестве роли не играет.

Рассмотрим ещё пару множеств: $X=\$ и $Y=\$. Каждый элемент множества $X$ является также элементом множества $Y$; каждый элемент множества $Y$ является также элементом множества $X$. Следовательно, $\=\$. С учётом подобных равенств в теории множеств принято одинаковые элементы не повторять в записи дважды. Например, множество цифр числа 1111111555559999 будет таким: $\$. Есть, конечно, исключения: так называемые мультимножества. В записи мультимножеств элементы могут повторяться, однако в классической теории множеств повторения элементов не допускаются.

Используя понятие равенства множеств, можно классифицировать подмножества.

Если $A\subseteq B$, при этом $A\neq B$, то множество $A$ называют собственным (строгим) подмножеством множества $B$. Также говорят, что множество $A$ строго включено в множество $B$. Записывают это так: $A \subset B$.

Если же некое подмножество множества $A$ совпадает с самим множеством $A$, то это подмножество называют несобственным. Иными словами, множество $A$ является несобственным подмножеством самого множества $A$.

Например, для рассмотренных выше множеств $K=\< -9,5\>$ и $T=\$ имеем: $K\subseteq T$, при этом $K\neq T$. Следовательно, множество $K$ является собственным подмножеством множества $T$, что записывается как $K\subset T$. Можно сказать и так: множество $K$ строго включено в множество $T$. Запись $K\subset T$ более конкретна, нежели $K\subseteq T$. Дело в том, что записывая $K\subset T$ мы гарантируем, что $K\neq T$. В то время как запись $K\subseteq T$ не исключает случая равенства $K=T$.

Примечание относительно терминологии: показать\скрыть

Вообще говоря, тут есть некая путаница в терминологии. Приведённое выше определение несобственных множеств принято в американской и части отечественной литературы. Однако в другой части отечественной литературы есть несколько иная трактовка понятия несобственных множеств.

Если $A\subseteq B$, при этом $A\neq B$ и $A\neq \varnothing$, то множество $A$ называют собственным (строгим) подмножеством множества $B$. Также говорят, что множество $A$ строго включено в множество $B$. Записывают это так: $A \subset B$. Множества $B$ и $\varnothing$ именуются несобственными подмножествми множества $B$.

Иными словами, пустое множество в такой трактовке исключается из собственных подмножеств и переходит в разряд несобственных. Выбор терминологии – дело вкуса.

Множество всех подмножеств некоего множества $A$ называют булеаном или степенью множества $A$. Обозначается булеан как $P(A)$ или $2^A$.

Пусть множество $A$ содержит $n$ элементов. Булеан множества $A$ содержит $2^n$ элементов, т.е.

Рассмотрим пару примеров на использование введённых выше понятий.

Из предложенного списка выберите те утверждения, которые являются верными. Ответ аргументируйте.

Нам заданы два множества: $\$ и $\$. Каждый элемент первого множества является также элементом второго множества. Следовательно, первое множество есть подмножество второго, т.е. $\\subseteq \$. Утверждение первого пункта – верное.
В первом пункте мы выяснили, что $\\subseteq \$. При этом данные множества не равны между собой, т.е. $\\neq \$. Значит, множество $\$ является собственным (в иной терминологии строгим) подмножеством множества $\$. Этот факт записывается как $\\subset \ $. Итак, утверждение второго пункта истинно.
Множество $\$ не является элементом множества $\$. Утверждение третьего пункта ложно. Для сравнения: утверждение $\\in \, 6 \>$ истинно.
Пустое множество является подможеством любого множества. Поэтому утверждение $\varnothing \subseteq \varnothing$ истинно.
Утверждение ложно. Множество $\varnothing$ не содержит элементов, а множество $\$ содержит один элемент, посему равенство $\varnothing=\$ неверно. Чтобы это было нагляднее, можно обратиться к той аналогии, что я описал выше. Множество – это портфель. Пустое множество $\varnothing$ – пустой портфель. Множество $\$ – портфель, внутри которого лежит пустой портфель. Естественно, что пустой портфель и непустой портфель, внутри которого нечто есть – разные портфели :)
Пустое множество не содержит элементов. Ни единого. Поэтому утверждение $\varnothing \in \varnothing$ ложно. Для сравнения: утверждение $\varnothing\in\$ истинно.
Множество $A$ содержит 4 элемента, а именно: 9, -5, 8 и $\$. Поэтому мощность множества $A$ равна 4, т.е. $|A|=4$. Следовательно, утверждение о том, что $|A|=5$ – ложно.

Ответ: Утверждения в пунктах №1, №2, №4 – истинны.

Записать булеан множества $A=\$.

Множество $A$ содержит 3 элемента. Иными словами: мощность множества $A$ равна 3, $|A|=3$. Следовательно, множество $A$ имеет $2^3=8$ подмножеств, т.е. булеан множества $A$ будет состоять из восьми элементов. Перечислим все подмножества множества $A$. Напомню, что пустое множество $\varnothing$ является подмножеством любого множества. Итак, подмножества таковы:

Напомню, что подмножество $\$ является несобственным, так как совпадает с множеством $A$. Все остальные подмножества – собственные. Все записанные выше подмножества являются элементами булеана множества $A$. Итак:

Булеан найден, остаётся лишь записать ответ.

Способы задания множеств.

Первый способ – это простое перечисление элементов множества. Естественно, такой способ подходит лишь для конечных множеств. Например, с помощью данного способа множество первых трёх натуральных чисел будет записано так:

Часто в литературе можно встретить обозначения такого характера: $T=\$. Здесь множество задаётся не перечислением элементов, как кажется на первый взгляд. Перечислить все чётные неотрицательные числа, которые и составляют множество $T$, невозможно, ибо этих чисел бесконечно много. Запись вида $T=\$ допускается только тогда, когда не вызывает разночтений.

Второй способ – задать множество с помощью так называемого характеристического условия (характеристического предиката) $P(x)$. В этом случае множество записывается в таком виде:

Запись $\$ читается так: "множество всех элементов $x$, для которых высказывание $P(x)$ истинно". Что именно значит словосочетание "характеристическое условие" проще пояснить на примере. Рассмотрим такое высказывание:

$$P(x)="x\; – \;натуральное\; число,\; последняя\; цифра\; которого \;равна\; 7"$$

Подставим в это высказывание вместо $x$ число 27. Мы получим:

$$P(27)="27\; – \;натуральное\; число,\; последняя\; цифра\; которого \;равна\; 7"$$

Это истинное высказывание, так как 27 действительно является натуральным числом, последняя цифра которого равна 7. Подставим в это высказывание число $\frac$:

$$P\left(\frac\right)="\frac\; – \;натуральное\; число,\; последняя\; цифра\; которого \;равна\; 7"$$

Это высказывание ложно, так как $\frac$ не является натуральным числом. Итак, для некоторых объектов $x$ высказывание $P(x)$ может быть ложно, для некоторых – истинно (а для некоторых вообще не определено). Нас будут интересовать лишь те объекты, для которых высказывание $P(x)$ будет истинно. Именно эти объекты и образуют множество, заданное с помощью характеристического условия $P(x)$ (см. пример №3).

Третий способ – задать множество с помощью так называемой порождающей процедуры. Порождающая процедура описывает, как получить элементы множества из уже известных элементов или неких иных объектов (см. пример №4).

Записать множество $A=\$ перечислением элементов.

Множество $A$ теперь задано с помощью перечисления элементов.

Описать элементы множества $M$, которое задано такой порождающей процедурой:

$3\in M$;
Если элемент $x\in M$, то $3x\in M$.
Множество $M$ – является подмножеством любого множества $A$, удовлетворяющего условиям №1 и №2.

Давайте пока оставим в покое условие №3 и посмотрим, какие элементы входят в множество $M$. Число 3 туда входит согласно первому пункту. Так как $3\in M$, то согласно пункту №2 имеем: $3\cdot 3\in M$, т.е. $9\in M$. Так как $9\in M$, то согласно пункту №2 получим: $3\cdot 9\in M$, т.е. $27\in M$. Так как $27\in M$, то по тому же пункту №2 имеем: $81\in M$. Короче говоря, построенное множество 3, 9, 27, 81 и так далее – это натуральные степени числа 3.

$$3^1=1; \; 3^2=9; \; 3^3=27; \; 3^4=81;\; \ldots$$

Итак, кажется, что искомое множество задано. И выглядит оно так: $\<3,9,27,81,\ldots \>$. Однако действительно ли условия №1 и №2 определяют только это множество?

Рассмотрим множество всех натуральных чисел, т.е. $N$. Число 3 – натуральное, посему $3\in N$. Вывод: множество $N$ удовлетворяет пункту №1. Далее, для любого натурального числа $x$ множество $N$ содержит также и число $3x$. Например, 5 и 15, 7 и 21, 13 и 39 и так далее. Значит, множество $N$ удовлетворяет условию №2. И, кстати сказать, не только множество $N$ удовлетворяет условиям №1 и №2. Например, множество всех нечётных натуральных чисел $N_1=\$ тоже подходит под условия пунктов №1 и №2. Как же указать, что нам нужно именно множество $\<3,9,27,81,\ldots \>$?

Вот тут на помощь приходит пункт №3. Говоря огрублённо, он означает, что множество $M$ – наименьшее из всех возможных множеств. Так как множества $N$ и $\<3,9,27,81,\ldots \>$ удовлетворяют пунктам №1 и №2, но $N\nsubseteq \<3,9,27,81,\ldots \>$, то множество $N$ не удовлетворяет третьему пункту. Аналогично, так как $N_1\nsubseteq \<3,9,27,81,\ldots \>$, то множество $N_1$ также не удовлетворяет пункту №3. Можно показать (если это необходимо, отпишите мне на почту, я распишу подробнее), что всем трём пунктам удовлетворяет лишь множество $\<3,9,27,81,\ldots \>$, т.е.

Обычно при задании множества с помощью таких правил (которые часто называют рекурсивными или индуктивными) третий пункт подразумевается, но не оговаривается явно. Но нужно иметь его в виду.

Заметили ошибку, опечатку, или некорректно отобразилась формула? Отпишите, пожалуйста, об этом в данной теме на форуме (регистрация не требуется).

Читайте также: