Информативным является сообщение квадрат гипотенузы равен сумме квадратов

Обновлено: 05.07.2024

На данный момент в научной литературе зафиксировано 367 доказательств данной теоремы. Вероятно, теорема Пифагора является единственной теоремой со столь внушительным числом доказательств. Такое многообразие можно объяснить лишь фундаментальным значением теоремы для геометрии.
Разумеется, концептуально все их можно разбить на малое число классов. Самые известные из них: доказательства методом площадей, аксиоматические и экзотические доказательства (например с помощью дифференциальных уравнений).

Через подобные треугольники

Следующее доказательство алгебраической формулировки — наиболее простое из доказательств, строящихся напрямую из аксиом. В частности, оно не использует понятие площади фигуры.
Пусть ABC есть прямоугольный треугольник с прямым углом C. Проведём высоту из C и обозначим её основание через H. Треугольник ACH подобен треугольнику ABC по двум углам. Аналогично, треугольник CBH подобен ABC. Введя обозначения

получаем

Что эквивалентно

Сложив, получаем

или

Доказательства методом площадей

Ниже приведённые доказательства, несмотря на их кажущуюся простоту, вовсе не такие простые. Все они используют свойства площади, доказательства которых сложнее доказательства самой теоремы Пифагора.

Доказательство через равнодополняемость

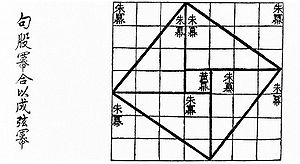
1. Расположим четыре равных прямоугольных треугольника так, как показано на рисунке.
2. Четырёхугольник со сторонами c является квадратом, так как сумма двух острых углов 90°, а развёрнутый угол — 180°.
3. Площадь всей фигуры равна, с одной стороны, площади квадрата со стороной (a+b), а с другой стороны, сумме площадей четырёх треугольников и внутреннего квадрата.

Что и требовалось доказать.

Доказательства через равносоставленность

Пример одного из таких доказательств указан на чертеже справа, где квадрат, построенный на гипотенузе, перестановкой преобразуется в два квадрата, построенных на катетах.

Идея доказательства Евклида состоит в следующем: попробуем доказать, что половина площади квадрата, построенного на гипотенузе, равна сумме половин площадей квадратов, построенных на катетах, а тогда и площади большого и двух малых квадратов равны. Рассмотрим чертеж слева. На нём мы построили квадраты на сторонах прямоугольного треугольника и провели из вершины прямого угла С луч s перпендикулярно гипотенузе AB, он рассекает квадрат ABIK, построенный на гипотенузе, на два прямоугольника — BHJI и HAKJ соответственно. Оказывается, что площади данных прямоугольников в точности равны площадям квадратов, построенных на соответствующих катетах. Попытаемся доказать, что площадь квадрата DECA равна площади прямоугольника AHJK Для этого воспользуемся вспомогательным наблюдением: Площадь треугольника с той же высотой и основанием, что и данный прямоугольник, равна половине площади заданного прямоугольника. Это следствие определения площади треугольника как половины произведения основания на высоту. Из этого наблюдения вытекает, что площадь треугольника ACK равна площади треугольника AHK (не изображённого на рисунке), которая, в свою очередь, равна половине площади прямоугольника AHJK. Докажем теперь, что площадь треугольника ACK также равна половине площади квадрата DECA. Единственное, что необходимо для этого сделать, — это доказать равенство треугольников ACK и BDA (так как площадь треугольника BDA равна половине площади квадрата по указанному выше свойству). Равенство это очевидно, треугольники равны по двум сторонам и углу между ними. Именно — AB=AK,AD=AC — равенство углов CAK и BAD легко доказать методом движения: повернём треугольник CAK на 90° против часовой стрелки, тогда очевидно, что соответствующие стороны двух рассматриваемых треугольников совпадут (ввиду того, что угол при вершине квадрата — 90°). Рассуждение о равенстве площадей квадрата BCFG и прямоугольника BHJI совершенно аналогично. Тем самым мы доказали, что площадь квадрата, построенного на гипотенузе, слагается из площадей квадратов, построенных на катетах.

Сложно представить, но в научной литературе существует 367 доказательств теоремы Пифагора. В школьной программе мы проходим гораздо меньше — в этом материале познакомимся с главными формулами и их доказательствами.

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Основные понятия

Теорема Пифагора, определение: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

Гипотенуза — сторона, лежащая напротив прямого угла.

Катет — одна из двух сторон, образующих прямой угол.

Формула Теоремы Пифагора выглядит так:

где a, b — катеты, с — гипотенуза.

Из этой формулы можно вывести следующее:

a = √c 2 − b 2
b = √c 2 − a 2
c = √a 2 + b 2

в любом прямоугольном треугольнике сумма квадратов длин двух катетов равна квадрату длины гипотенузы.

Для треугольника со сторонами a, b и c, где c — большая сторона, действуют следующие правила:

если c 2 2 + b 2 , значит угол, противолежащий стороне c, является острым.
если c 2 = a 2 + b 2 , значит угол, противолежащий стороне c, является прямым.
если c 2 > a 2 +b 2 , значит угол, противолежащий стороне c, является тупым.

Теорема Пифагора: доказательство

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Дано: ∆ABC, в котором ∠C = 90º.

Доказать: a 2 + b 2 = c 2 .

Пошаговое доказательство:

Проведём высоту из вершины C на гипотенузу AB, основание обозначим буквой H.
Прямоугольная фигура ∆ACH подобна ∆ABC по двум углам:

Введем новые обозначения: BC = a, AC = b, AB = c.

Из подобия треугольников получим: a : c = HB : a, b : c = AH : b.

Значит a 2 = c * HB, b 2 = c * AH.
Сложим полученные равенства:

a 2 + b 2 = c * HB + c * AH

a 2 + b 2 = c * (HB + AH)

a 2 + b 2 = c * AB

Обратная теорема Пифагора: доказательство

Если сумма квадратов двух сторон треугольника равна квадрату третьей стороны, то такой треугольник является прямоугольным.

Дано: ∆ABC

Доказать: ∠C = 90º

Пошаговое доказательство:

Построим прямой угол с вершиной в точке C₁.
Отложим на его сторонах отрезки C₁A₁ = CA и C₁B₁ = CB.

Проведём отрезок A₁B₁.
Получилась фигура ∆A₁B₁C₁, в которой ∠C₁=90º.

В этой фигуре ∆A₁B₁C₁ применим теорему Пифагора: A₁B₁ 2 = A₁C₁ 2 + B₁C₁ 2 .
Таким образом получится:

Значит, в фигурах треугольниках ∆ABC и ∆A₁B₁C₁:

C₁A₁ = CA и C₁B₁ = CB по результату построения,
A₁B₁ = AB по доказанному результату.

Поэтому, ∆A₁B₁C₁ = ∆ABC по трем сторонам.
Из равенства фигур следует равенство их углов: ∠C =∠C₁ = 90º.

Обратная теорема доказана.

Решение задач

Задание 1. Дан прямоугольный треугольник ABC. Его катеты равны 6 см и 8 см. Какое значение у гипотенузы?

Как решаем:

Пусть катеты a = 6 и b = 8.

По теореме Пифагора c 2 = a 2 + b 2 .

Подставим значения a и b в формулу:
c 2 = 6 2 + 8 2 = 36 + 64 = 100
c = √100 = 10.

Теорема Пифагора — одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника.

Содержание

Формулировки

Теорема Пифагора: Сумма площадей квадратов, опирающихся на катеты (a и b), равна площади квадрата, построенного на гипотенузе (c).

Геометрическая формулировка:

Изначально теорема была сформулирована следующим образом:

В прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах.

Алгебраическая формулировка:

В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

То есть, обозначив длину гипотенузы треугольника через c , а длины катетов через a и b :

a 2 + b 2 = c 2

Обе формулировки теоремы эквивалентны, но вторая формулировка более элементарна, она не требует понятия площади. То есть второе утверждение можно проверить, ничего не зная о площади и измерив только длины сторон прямоугольного треугольника.

Обратная теорема Пифагора:

Для всякой тройки положительных чисел a , b и c , такой, что a 2 + b 2 = c 2 , существует прямоугольный треугольник с катетами a и b и гипотенузой c .

Доказательства

На данный момент в научной литературе зафиксировано 367 доказательств данной теоремы [1] . Вероятно, теорема Пифагора является единственной теоремой со столь внушительным числом доказательств. Такое многообразие можно объяснить лишь фундаментальным значением теоремы для геометрии.

Разумеется, концептуально все их можно разбить на малое число классов. Самые известные из них: доказательства методом площадей, аксиоматические и экзотические доказательства (например с помощью дифференциальных уравнений).

Через подобные треугольники

Пусть ABC есть прямоугольный треугольник с прямым углом C. Проведём высоту из C и обозначим её основание через H. Треугольник ACH подобен треугольнику ABC по двум углам. Аналогично, треугольник CBH подобен ABC. Введя обозначения

$|BC|=a, |AC|=b, |AB|=c\,$

$\frac =\frac<|HB|>; \frac=\frac<|AH|>.$

$a^2=c\cdot |HB|; b^2=c\cdot |AH|.\,$

$a^2+b^2=c\cdot\left(|HB|+|AH|\right)=c^2.$

$a^2+b^2=c^2\,$

Доказательства методом площадей

Доказательство через равнодополняемость

Расположим четыре равных прямоугольных треугольника так, как показано на рисунке 1.
Четырёхугольник со сторонами c является квадратом, так как сумма двух острых углов 90°, а развёрнутый угол — 180°.
Площадь всей фигуры равна, с одной стороны, площади квадрата со стороной (a+b), а с другой стороны, сумме площадей четырёх треугольников и двух внутренних квадратов.

Что и требовалось доказать.

Доказательства через равносоставленность

Доказательство Евклида

Рассмотрим чертеж слева. На нём мы построили квадраты на сторонах прямоугольного треугольника и провели из вершины прямого угла С луч s перпендикулярно гипотенузе AB, он рассекает квадрат ABIK, построенный на гипотенузе, на два прямоугольника — BHJI и HAKJ соответственно. Оказывается, что площади данных прямоугольников в точности равны площадям квадратов, построенных на соответствующих катетах.

Попытаемся доказать, что площадь квадрата DECA равна площади прямоугольника AHJK Для этого воспользуемся вспомогательным наблюдением: Площадь треугольника с той же высотой и основанием, что и данный прямоугольник, равна половине площади заданного прямоугольника. Это следствие определения площади треугольника как половины произведения основания на высоту. Из этого наблюдения вытекает, что площадь треугольника ACK равна площади треугольника AHK (не изображённого на рисунке), которая, в свою очередь, равна половине площади прямоугольника AHJK.

Докажем теперь, что площадь треугольника ACK также равна половине площади квадрата DECA. Единственное, что необходимо для этого сделать, — это доказать равенство треугольников ACK и BDA (так как площадь треугольника BDA равна половине площади квадрата по указанному выше свойству). Равенство это очевидно, треугольники равны по двум сторонам и углу между ними. Именно — AB=AK,AD=AC — равенство углов CAK и BAD легко доказать методом движения: повернём треугольник CAK на 90° против часовой стрелки, тогда очевидно, что соответствующие стороны двух рассматриваемых треугольников совпадут (ввиду того, что угол при вершине квадрата — 90°).

Рассуждение о равенстве площадей квадрата BCFG и прямоугольника BHJI совершенно аналогично.

Тем самым мы доказали, что площадь квадрата, построенного на гипотенузе, слагается из площадей квадратов, построенных на катетах. Идея данного доказательства дополнительно проиллюстрирована с помощью анимации, расположенной выше.

Доказательство Леонардо да Винчи

Главные элементы доказательства — симметрия и движение.

Рассмотрим чертёж, как видно из симметрии, отрезок CI рассекает квадрат ABHJ на две одинаковые части (так как треугольники ABC и JHI равны по построению). Пользуясь поворотом на 90 градусов против часовой стрелки, мы усматриваем равенство заштрихованных фигур CAJI и GDAB . Теперь ясно, что площадь заштрихованной нами фигуры равна сумме половин площадей квадратов, построенных на катетах, и площади исходного треугольника. С другой стороны, она равна половине площади квадрата, построенного на гипотенузе, плюс площадь исходного треугольника. Последний шаг в доказательстве предоставляется читателю.

Доказательство методом бесконечно малых

Следующее доказательство при помощи дифференциальных уравнений часто приписывают известному английскому математику Харди, жившему в первой половине XX века.

Рассматривая чертёж, показанный на рисунке, и наблюдая изменение стороны a, мы можем записать следующее соотношение для бесконечно малых приращений сторон с и a (используя подобие треугольников):

$\frac <da> = \frac$

Пользуясь методом разделения переменных, находим

$c\, dc = a\, da$

Более общее выражение для изменения гипотенузы в случае приращений обоих катетов

$c\ dc = a\, da + b\, db$

Интегрируя данное уравнение и используя начальные условия, получаем

$a = b = c = 0 \Rightarrow \mathrm<constant> c 2 = a 2 + b 2 + constant. = 0$

Таким образом, мы приходим к желаемому ответу

c 2 = a 2 + b 2 .

Как нетрудно видеть, квадратичная зависимость в окончательной формуле появляется благодаря линейной пропорциональности между сторонами треугольника и приращениями, тогда как сумма связана с независимыми вкладами от приращения разных катетов.

Более простое доказательство можно получить, если считать, что один из катетов не испытывает приращения (в данном случае катет b ). Тогда для константы интегрирования получим

$a=0 \Rightarrow c^2 = b^2 = \mathrm<constant> .$

Вариации и обобщения

$c^2=a^2+b \cdot d$

В любом равнобедренном треугольнике верно следующее соотношение (см. рисунок внизу справа) [2] :

Если вместо квадратов построить на катетах другие подобные фигуры, то верно следующее обобщение теоремы Пифагора: В прямоугольном треугольнике сумма площадей подобных фигур, построенных на катетах, равна площади фигуры, построенной на гипотенузе. В частности:
- Сумма площадей правильных треугольников, построенных на катетах, равна площади правильного треугольника, построенного на гипотенузе.
- Сумма площадей полукругов, построенных на катетах (как на диаметре), равна площади полукруга, построенного на гипотенузе. Этот пример используется при доказательстве свойств фигур, ограниченных дугами двух окружностей и носящих имя гиппократовых луночек.
- В случае ортогональной системы векторов \frac<><>" width="" height="" />
 имеет место равенство, также называемое теоремой Пифагора: ^ \|v_k \|^2 = \left\|\sum_^ v_k \right\|^2. " width="" height="" />
 - Если \frac<><>" width="" height="" />
 — это проекции вектора на координатные оси, то эта формула совпадает с расстоянием Евклида и означает, что длина вектора есть корень квадратный из суммы квадратов его компонентов.
 - Аналог этого равенства в случае бесконечной системы векторов носит название равенства Парсеваля.
 История
 
 Чу-пей 500–200 до нашей эры. Слева надпись: сумма квадратов длин высоты и основания есть квадрат длины гипотенузы.
 
 В древнекитайской книге Чу-пей говорится о пифагоровом треугольнике со сторонами 3, 4 и 5: В этой же книге предложен рисунок, который совпадает с одним из чертежей индусской геометрии Басхары.
 
 Кантор (крупнейший немецкий историк математики) считает, что равенство 3 ² + 4 ² = 5² было известно уже египтянам еще около 2300 г. до н. э., во времена царя Аменемхета I (согласно папирусу 6619 Берлинского музея). По мнению Кантора гарпедонапты, или "натягиватели веревок", строили прямые углы при помощи прямоугольных треугольников со сторонами 3, 4 и 5.
 
 Очень легко можно воспроизвести их способ построения. Возьмем веревку длиною в 12 м. и привяжем к ней по цветной полоске на расстоянии 3м. от одного конца и 4 метра от другого . Прямой угол окажется заключенным между сторонами длиной в 3 и 4 метра. Гарпедонаптам можно было бы возразить, что их способ построения становиться излишним, если воспользоваться, например, деревянным угольником, применяемым всеми плотниками. И действительно, известны египетские рисунки, на которых встречается такой инструмент, например рисунки, изображающие столярную мастерскую.
 
 Несколько больше известно о теореме Пифагора у вавилонян. В одном тексте, относимом ко времени Хаммураби, т. е. к 2000 г. до н. э., приводится приближенное вычисление гипотенузы прямоугольного треугольника [3] . Отсюда можно сделать вывод, что в Двуречье умели производить вычисления с прямоугольными треугольниками, по крайней мере в некоторых случаях. Основываясь, с одной стороны, на сегодняшнем уровне знаний о египетской и вавилонской математике, а с другой-на критическом изучении греческих источников, Ван-дер-Варден (голландский математик) сделал следующий вывод:
 
 Весьма вероятно, что теорема о квадрате гипотенузы была известна в Индии уже около 18 века до н. э.
 
 Презентация на тему: " Теорема Пифагора Квадрат гипотенузы равен сумме квадратов катетов." — Транскрипт:
 
 2 Теорема Пифагора Квадрат гипотенузы равен сумме квадратов катетов
 
 3 Это прямоугольный треугольник
 
 4 катет гипотенуза a c b
 
 5 a c b Выполним дополнительные построения
 
 6 a a a a b b b b c c c c
 
 7 a a a a b b b b c c c c Это квадрат Его площадь равна 2 (а+b)
 
 8 a a a a b b b b c c c c Это тоже квадрат Его площадь равна 2 с
 
 9 a a a a b b b b c c c c Площадь этого треугольника 1/2ab
 
 10 a a a a b b b b c c c c Площадь большого квадрата равна сумме площадей маленького квадрата и площадей 4-х треугольников. (a+b)2=c2+4*1/2ab отсюда a2+2ab+b2=c2+2ab a2+b2=c2
 
 Похожие презентации
 
 с с b b b b а а а а Дано: Прямоугольный треугольник а и b – катеты с – гипотенуза Доказать: с 2 =а 2 +b 2 Доказательство: 1.Достроим треугольник до квадрата.
 
 Какой треугольник называется прямоугольным? Как называются его стороны? Катеты и гипотенуза.
 
 Кураева Маргарита 8А класс. с с b b b b а а а а Дано: Прямоугольный треугольник а и b – катеты с – гипотенуза Доказать: с 2 =а 2 +b 2 Доказательство:
 
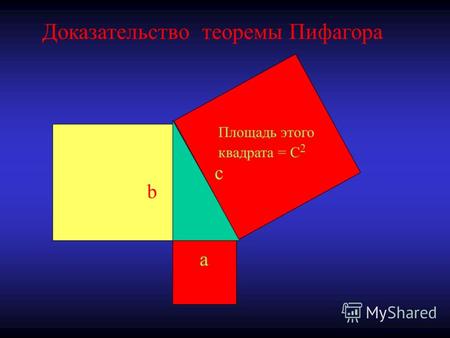
 C a b Доказательство теоремы Пифагора Площадь этого квадрата = C 2.
 
 Теорема Пифагора Теорема В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. В А С.
 
 Теорема Пифагора Квадрат гипотенузы равен сумме квадратов катетов.
 
 Лабораторная работа. Задание 1 n Начертите прямой угол. n Отложим на его сторонах катеты 3 м и 4 м. (Масштаб: клеточка равна 1 метру.) n Получим гипотенузу,
 
 1 вариант. Составьте уравнение с двумя переменными, если: Сумма двух натуральных чисел равна 16. Периметр прямоугольника равен 12 см. Одна сторона прямоугольника.
 
 Теорема Пифагора. Дано: + = Найти: Задача N А В СD M K P Доказать, что KMNP- квадрат.
 
 Теорема Пифагора. Формулировки теоремы Геометрическая Геометрическая Геометрическая Алгебраическая Алгебраическая Алгебраическая.
 
 Теорема Пифагора Автор: ученик 5 класса Поскребышев Иван.
 
 ТЕОРЕМА ПИФАГОРА Проверка домашнего задания 501 Площадь земельного участка равна 27 га. Выразите площадь этого же участка: а) в квадратных метрах; Б)
 
 Геометрия Геометрия Выполнила:КарташоваЮлия 8 класс.
 
 Теорема Пифагора* Презентация посвящена одной из теорем Пифагора, значение которой для геометрии очень велико. Дальше мы в этом убедимся. А также ознакомимся.
 
 Презентация к уроку по геометрии по теме: теорема Пифагора
 
 Какой треугольник изображен на рисунке? M K P. a b c Чем является отрезок a ?
 
 Теорема Пифагора задачи задачи. Формулировки и формула Сформулируйте и запишите с помощью букв a, b и c теорему Пифагора. Сформулируйте теорему, обратную.
 
 ТРЕУГОЛЬНИК – ЭТО ГЕОМЕТРИЧЕСКАЯ ФИГУРА, СОСТОЯЩАЯ ИЗ ТРЁХ ТОЧЕК, СОЕДИНЁННЫХ МЕЖДУ СОБОЙ ОТРЕЗКАМИ ТОЧКИ – ВЕРШИНЫ. ОТРЕЗКИ – СТОРОНЫ. ДОМОЙ.
 
 Теорема Пифагора и способы её доказательства Пифагор около 570 г. до н.э.
 
 Подбираем похожую презентацию.
 
 Теорема Пифагора* Презентация посвящена одной из теорем Пифагора, значение которой для геометрии очень велико. Дальше мы в этом убедимся. А также ознакомимся.
 
 Теорема Пифагора — квадрат гипотенузы равен сумме квадратов катетов (в прямоугольном треугольнике); формула: c² = a² + b².
 
 Доказательство
 
 Доказательство теоремы Пифагора, используя алгебру
 
 Нужно доказать, что c² = a² + b²:
 
 Это квадрат, в котором есть 4 одинаковых треугольника abc:
 1. Каждая сторона этого квадрата имеет длину a + b, значит его общая площадь: A = (a + b) (a + b);
 2. Площадь наименьшего квадрата (который находится внутри, под наклоном): c²;
 3. Площадь каждого из треугольников: ab/2. Значит площадь всех четырёх вместе: 4ab/2 = 2ab;
 4. Сумма наименьшего квадрата и треугольников: A = c² + 2ab;
 5. Площадь большого квадрата (A = (a + b) (a + b)) равна сумме наименьшего квадрата со всеми треугольниками. Значит:
 (a + b) (a + b) = c² + 2ab
 
 a² + 2ab + b² = c² + 2ab
 
 Что и требовалось доказать.
 
 "Пифагоровы штаны на все стороны равны"
 
 Это шуточная фраза, которая именует ещё одно доказательство теоремы Пифагора
 
 На этой фигуре c — гипотенуза, a и b — катеты.
 
 Проведём перпендикулярную линию к гипотенузе (c):
 
 Таким образом появились два новых прямоугольных треугольника (A и B) внутри большого (исходный треугольник С).
 1. Общая площадь исходного треугольника (С) равна сумме двух новых, маленьких (A и B): С = А + B;
 2. Делим "Пифагоровы штаны" на 3 похожие фигуры:
 Что и требовалось доказать.
 
 Примеры
 
 Задача 1
 
 На рисунке видно, что длина одной стороны прямоугольного треугольника составляет 3 см, длина другой — 4 см. Найдите длину гипотенузы.
 
 Подставить известные значения
 
 Ответ: длина гипотенузы равна 5.
 
 Задача 2
 
 Длина одной стороны прямоугольного треугольника составляет 12 см, длина гипотенузы 13 см. Найдите длину другой стороны треугольника.
 
 Подставить известные значения
 
 Ответ: длина другой стороны треугольника равна 5.
 
 Следствия из теоремы Пифагора
 
 Это основные следствия теоремы:
 1. В прямоугольном треугольнике гипотенуза всегда больше любого из двух катетов.
 2. Если применить формулу теоремы Пифагора (c² = a² + b²) и равенство будет верным, (т.е. если квадрат одной стороны равен сумме квадратов двух других сторон), то треугольник прямоугольный.
 3. Из формулы теоремы Пифагора также можно посчитать любой из катетов: a² = c² − b² либо b² = c² − a².
 4. Любой косинус (cos) острого угла будет меньше 1.
 Кто придумал теорему Пифагора
 
 Концепция теоремы Пифагора была известна ещё в древнем Египте и Вавилоне (около 1900 г. до н. э.). Связь между катетами и гипотенузой в прямоугольном треугольнике была изображена на вавилонской глиняной табличке (которой около 4000 лет). Однако это знание стало широко использоваться лишь после того, как сам Пифагор заявил о нём (он жил в 6 веке до н. э.).
 
 Читайте также: