Сочинение по геометрии на тему квадрат 8 класс

Обновлено: 02.07.2024

Многоугольник — это фигура, составленная из отрезков так, что смежные отрезки не лежат на одной прямой, а несмежные отрезки не имеют общих точек.
Сумма длин всех сторон многоугольника называется периметром многоугольника.
Две вершины многоугольника, принадлежащие одной стороне, называются соседними.
Отрезок, соединяющий любые две несоседние вершины, называется диагональю многоугольника.
Многоугольник называется выпуклым, если он лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины.
Сумма углов выпуклого n-угольника равна (n–2)·180°.
Четырёхугольник – это многоугольник у которого четыре вершины и четыре стороны.
Две несмежные стороны четырёхугольника называются противоположными.
Две вершины, не являющиеся соседними, называются противоположными.
Сумма углов выпуклого четырехугольника равна 360°. называется четырехугольник, у которого противоположные стороны попарно параллельны.
(Свойства параллелограмма) В параллелограмме противоположные стороны равны и противоположные углы равны. Диагонали параллелограмма точкой пересечения делятся пополам.
(Признак параллелограмма) Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник — параллелограмм.
(Признак параллелограмма) Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм.
(Признак параллелограмма) Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.
Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны. Параллельные стороны трапеции называются ее основаниями, а две другие стороны — боковыми сторонами.
Трапеция называется равнобедренной, если её боковые стороны равны.
Трапеция называется прямоугольной, если один из её углов прямой.
(Т. Фалеса) Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.
Прямоугольником называется параллелограмм, у которого все углы прямые.
(Особое свойство прямоугольника) Диагонали прямоугольника равны.
(Признак прямоугольника) Если в параллелограмме диагонали равны, то этот параллелограмм — прямоугольник.
Ромбом называется параллелограмм, у которого все стороны равны.
(Особое свойство ромба) Диагонали ромба взаимно перпендикулярны и делят его углы пополам.
Квадратом называется прямоугольник, у которого все стороны равны.
(Основные свойства квадрата) Все углы квадрата прямые. Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам.
Две точки А и А₁ называются симметричными относительно прямой а, если эта прямая проходит через середину отрезка АА₁ и перпендикулярна к нему.
Две точки А и А₁ называются симметричными относительно точкиО, если О – середина отрезка АА_1.
(Основные свойства площадей) Равные многоугольники имеют равные площади.
Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.
Площадь квадрата равна квадрату его стороны ( S=a 2 ).
(Т.)Площадь прямоугольника равна произведению его смежных сторон (S=ab).
(Т.)Площадь параллелограмма равна произведению его основания на высоту (S=ah).
(Т.)Площадь треугольника равна половине произведения его основания на высоту (S= ah).
Площадь прямоугольного треугольника равна половине произведения его катетов (S= ab).
Если высоты двух треугольников равны, то их площади относятся как основания.
Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы.
Площадь трапеции равна произведению полусуммы её оснований на высоту ( S= ·h ).
(Теорема Пифагора) В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. (с 2 =a 2 +b 2 )
(Теорема, обратная теореме Пифагора) Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный.
Треугольник со сторонами 3, 4, 5 называют египетским треугольником.
(Формула Герона) Площадь треугольника со сторонами a, b, c выражается формулой S= , где p = (a+b+c) - полупериметр треугольника.
Говорят, что отрезки AB и CD пропорциональны отрезкам A₁B₁ и C₁D_{1 ,} если = .
Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого.
Число k, равное отношению сходственных сторон подобных треугольников, называется коэффициентом подобия.
(Т.)Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
(Т. Первый признак подобия треугольников) Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
(Т. Второй признак подобия треугольников) Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.
(Т. Третий признак подобия треугольников) Если три стороны одного треугольника пропорциональны трём сторонам другого, то такие треугольники подобны.
Средняя линия треугольника — это отрезок, соединяющий середины двух его сторон.
(Т. о средней линии треугольника) Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины.
Высота прямоугольного треугольника, проведённая из вершины прямого угла, разделяет треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному треугольнику.
Отрезок XY называется средним пропорциональным (или средним геометрическим) для отрезков АВ и CD, если XY=
Средняя линия трапеции — это отрезок, соединяющий середины ее боковых сторон.
(Т. о средней линии трапеции) Средняя линия трапеции параллельна основаниям трапеции и равна их полусумме.
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету.
Тангенс угла равен отношению синуса к косинусу этого угла.
sin 2 A+cos 2 A=1 – основное тригонометрическое тождество.
Если расстояние от центра окружности до прямой меньше радиуса окружности, то прямая и окружность имеют две общие точки.
Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют одну общую точку.
Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общих точек.
Прямая, имеющая с окружностью только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности.
(Т. о свойстве касательной к окружности) Касательная к окружности перпендикулярна к радиусу, проведённому в точку касания.
(Свойство отрезков касательных, проведённых из одной точки) Отрезки касательных к окружности, проведённые из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
(Т. Признак касательной) Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна к этому радиусу, то она является касательной
Дуга называется полуокружностью, если отрезок, соединяющий её концы, является диаметром окружности.
Угол с вершиной в центре окружности называется её центральным углом.
Центральный угол измеряется дугой, на которую он опирается.
Сумма градусных мер двух дуг окружности с общими концами равна 360°.
Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом.
(Т.) Вписанный угол измеряется половиной дуги, на которую он опирается.
Вписанные углы, опирающиеся на одну и ту же дугу, равны.
Вписанный угол, опирающийся на полуокружность – прямой.
(Теорема о произведении отрезков пересекающихся хорд) Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
Каждая точка биссектрисы неразвёрнутого угла равноудалена от его сторон. Обратно: каждая точка, лежащая внутри угла и равноудалённая от сторон угла, лежит на его биссектрисе.
Биссектрисы треугольника пересекаются в одной точке.
Серединным перпендикуляром к отрезку называется прямая, проходящая через середину данного отрезка и перпендикулярная к нему.
(Теорема о серединном перпендикуляре к отрезку) Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. Обратно: каждая точка, равноудалённая от концов отрезка, лежит на серединном перпендикуляре к нему.
Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.
Высоты треугольника (или их продолжения) пересекаются в одной точке.
Четыре точки: точка пересечения медиан, точка пересечения биссектрис, точка пересечения серединных перпендикуляров к сторонам и точка пересечения высот(или их продолжений) называются замечательными точками треугольника.
Если все стороны многоугольника касаются окружности, то окружность называется вписанной в многоугольник, а многоугольник – описанным около этой окружности.
(Теорема об окружности, вписанной в треугольник) В любой треугольник можно вписать окружность.
В треугольник можно вписать только одну окружность.
Не во всякий четырёхугольник можно вписать окружность.
В любом описанном четырёхугольнике суммы противоположных сторон равны.
Если суммы противоположных сторон выпуклого четырёхугольника равны то в него можно вписать окружность.
Если все вершины многоугольника лежат на окружности, то окружность называется описанной около многоугольника, а многоугольник – вписанным в эту окружность.
(Теорема об окружности, описанной около треугольника) Около любого треугольника можно описать окружность.
Около треугольника можно описать только одну окружность.
Около четырёхугольника не всегда можно описать окружность.
В любом вписанном четырёхугольнике сумма противоположных углов равна 180°.
Если сумма противоположных углов четырёхугольника равна 180°, то около него можно описать окружность.

ABCDE — пятиугольник (рис. 11). Точки А, В, С, D, Е — вершины многоугольника; ∠A, ∠B, ∠C, ∠D, ∠E — углы; АВ, ВС, CD и т. д. — стороны; отрезки АС, AD, BE, BD, СЕ — диагонали; Р = АВ + ВС + … + ЕА — периметр многоугольника.
Многоугольник называется выпуклым (см. рис. 11), если он целиком расположен по одну сторону от каждой прямой, проходящей через две его соседние вершины. В противном случае многоугольник называется невыпуклым (рис. 12).

Свойства
1. Сумма внутренних углов произвольного n-угольника равна 180° • (n — 2).
2. Сумма внешних углов выпуклого n-угольника, взятых по одному при каждой вершине, равна 360°.
3. В выпуклом n-угольнике из каждой вершины можно провести (n — 3) диагоналей, которые разбивают n-угольник на (n — 2) треугольников.
4. В выпуклом n-угольнике число диагоналей равно n(n — 3)/2.

☑ 2. Правильные многоугольники

Выпуклый многоугольник, у которого равны все углы и стороны, называется правильным.
Свойства
1. Каждый угол правильного n-угольника равен а_n = 180°(n — 2)/n
2. Около правильного n-угольника можно описать окружность, и притом только одну.
3. В правильный n-угольник можно вписать окружность, и притом только одну.
4. Окружность, вписанная в правильный n-угольник, касается всех сторон n-угольника в их серединах.
5. Центр окружности, описанной около правильного n-угольника, совпадает с центром окружности, вписанной в тот же n-угольник.
6. Длина стороны правильного n-угольника, вписанного в окружность радиуса R, равна а = 2R sin(180°/n).
7. Длина стороны правильного n-угольника, описанного около окружности радиуса r, равна а = 2r tg(180°/n).

☑ 3. Четырехугольник

☑ 4. Параллелограмм

Признаки параллелограмма (рис. 48)

Если в четырехугольнике две стороны равны и параллельны (АВ = DC, АВ || CD), то такой четырехугольник — параллелограмм.
Если в четырехугольнике противоположные стороны попарно равны (АВ = DC, AD = DC), то такой четырехугольник — параллелограмм.
Если в четырехугольнике противоположные углы попарно равны (∠A = ∠C; ∠B = ∠D), то такой четырехугольник — параллелограмм.
Если в четырехугольнике диагонали пересекаются и в точке пересечения делятся пополам, то такой четырехугольник — параллелограмм.

☑ 5. Трапеция

Равнобедренная трапеция

Прямоугольная трапеция

☑ 6. Прямоугольник

☑ 7. Ромб

☑ 8. Квадрат

☑ 9. Теорема Чевы

☑ 10. Теорема Менедая

☑ 11. Теорема синусов

☑ 12. Теорема косинусов

☑ 13. Площадь треугольника

☑ 14. Площадь многоугольников

☑ 15. Равносторонний (правильный) треугольник

☑ 16. Подобные треугольники

☑ 17. Признаки подобия треугольников

☑ 18. Окружность

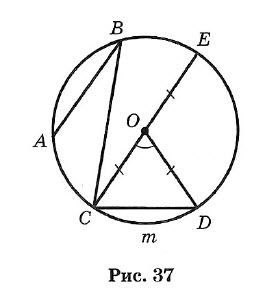
Окружностью называется геометрическое место точек плоскости, равноудаленных от одной ее точки (центра) (рис. 37).
Отрезок, соединяющий центр окружности с точкой на окружности, называется радиусом. Обозначение: г или R.
На рисунке ОС = ОЕ = OD = R.
Часть окружности (например, CmD) называется дугой.
Отрезок, соединяющий две точки окружности, называется хордой, а хорда, проходящая через центр, — диаметром.
АВ, ВС, CD и СЕ — хорды окружности. СЕ — наибольшая из хорд — диаметр.
Обозначение: d или D. D = 2R.
Часть плоскости, ограниченная окружностью, называется кругом.
Часть круга, ограниченная дугой (CmD) и стягивающей ее хордой (CD), называется сегментом.
Часть круга, ограниченная двумя радиусами и дугой, называется сектором.
Угол, образованный двумя радиусами, называется центральным (∠COD на рис. 37).
Угол, у которого вершина лежит на окружности, а стороны являются хордами, называется вписанным (например, ∠ABC).

☑ 19. Свойства касательных к окружности

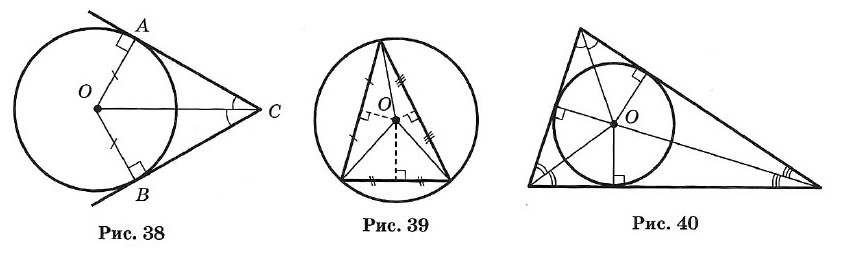
Угол, образованный двумя касательными (СА и СВ), исходящими из одной точки, называется описанным (∠ACB на рис. 38).
1. Радиус, проведенный в точку касания, перпендикулярен касательной.
2. Две касательные, проведенные к окружности из одной точки, равны, и центр окружности лежит на биссектрисе угла между ними.

☑ 20. Окружность и треугольник

1. Около всякого треугольника можно описать окружность; центром окружности является точка пересечения перпендикуляров, проведенных к сторонам через их середины (рис. 39).
2. Во всякий треугольник можно вписать окружность; центром окружности является точка пересечения биссектрис (рис. 40).

☑ 21. Окружность и четырехугольник

☑ 22. Углы и окружность

☑ 23. Метрические соотношения в окружности

☑ 24. Длина окружности. Площадь круга и его частей

☑ 25. Уравнение окружности

Цель обучения (когнитивная) Сформировать у учащихся определение квадрат. Изучить свойства квадрата для решения практических задач.

Цель личностного развития: Создать условия для развития коммуникативных навыков и познавательной активности учащихся через групповую форму работы.

А - знает определение квадрата, признаки и свойства ;

В – умеет изображать на рисунке четырехугольник, его стороны, вершины, углы, диагонали и высоты, решать геометрические задачи;

С – сможет пользоваться геометрическим языком для описания предметов окружающего мира

Оборудование: учебники, тетради, презентация , дополнительные ресурсы, стикеры, раздаточный материал, листы оценивания, постеры.

Оборудование: учебники, тетради,

1 Психологический настрой.

физминутка (проведение бодрячка ребенком)

2.Проверка домашнего задания

Презентация по теме: Ромб в геометрии и окружающем мире.

б) Распределение по группам по геометрическим фигурам (ромбы,

параллелограмм в одной группе разных цветов)

3.Создание проблемной ситуации

Посмотрите на свои фигуры

Все ли они вам знакомы?

Приглашаю одну девочку, на лоб прикрепляю стикер, которая должна отгадать слово, задавая наводящие вопросы классу.

Заостряю внимание на графе определение.

-Какую фигуру называют квадратом?

Защищают свои презентации

Участвуют в создании групп.

Ребята дают ответы,только да и нет

Заполнение таблицы графы знаю(индивидуально)

Решение задач с помощью свойств

Оценивание для обучения

Выразить свою радость через эмоции

Оценивание для обучения

II. Операционный этап.

4 Изучение нового

Сегодня мы поговорим о квадрате.

В этом вам поможет учебник и ресурс на столе

Задание: Собери из этих частей различные фигуры, например

Б) Решите задачу разными способами

Составление постера в группах.

Защита постера спикером,который остается вгруппе, а остальные участники перемещаются

Заполняют таблицу графу Узнал

Работают в группе

Работают в парах, записывают решение на листах А4,Обсуждают в группе,

находят наиболее рациональный способ.

Один из участников группы защищает, перемещаясь в другие группы

Каждая группа оценивает с помощью одного слова отношение к данной задаче

Оценивание для обучения.

наиболее понравившемуся постеру

Оценивание для обучения

Молодец!, понравилось и т.д.

Оценивание для обучения

Предлагаю заполнить графу в таблице Хочу узнать

Информация о домашнем задании:

Соберите фигуру из простого оригами

Заполнение третьей графы таблицы

Оценивание для обучения

Оценивают свое отношение к уроку

Оценивание для обучения

По теме: методические разработки, презентации и конспекты

Технологическая карта урока, реализующего формирование УУД по теме “Квадрат суммы и квадрат разности”

Тип урока: урок изучения нового материала Тема раздела: “Формулы сокращённого умножения” Тема урока: “Квадрат суммы и квадрат разности” Класс 7 .

Урок18. Технологическая карта урока для 5 класса по теме: "Сложение натуральных чисел и его свойства"

Технологическая карта составлена по учебнику: Математика. 5 класс: учеб. для общеобразовательных учреждений / Н.Я. Виленкин 2013г./.

Технологическая карта урока геометрии 8 класс Ромб и квадрат

Технологическая карта урока составлена в соответствии с требованиями ФГОС на оснолвании учебника: Атанасян Л.С., Бутузов В.Ф., С.Б. Кадомцев и др. Геометрия. 7-9 классы.-М.:Просвещение, 2016.Тип урока.

технологическая карта урока в 11 классе по теме "Основные характеристики, свойства и использование электромагнитных волн"

Данная разработка составлена с учетом требований ФГОС и с использованием регионального компонента.

Технологическая карта урока геометрии 7 класс на тему "Неравенство треугольника"

Технологическая карта урока геометрии 7 класс на тему "Неравенство треугольника".

Технологическая карта урока геометрии 7 класс " Применение свойств прямоугольных треугольников при решении задач."

Технологическая карта урока геометрии 7 класс по теме " Применение свойств прямоугольных треугольников при решении задач".

Технологическая карта урока геометрии 7 класса по теме "Признаки равенства прямоугольных треугольников".

В этом уроке мы рассмотрим такие геометрические фигуры, как ромб и квадрат. Введем понятие ромба. Узнаем, какими свойствами обладают диагонали ромба. Рассмотрим 2 признака ромба. Закрепим представления о квадрате. Вспомним основные свойства квадрата. И, конечно же, закрепим изученный материал в практической части урока.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.

Получите невероятные возможности

Конспект урока "Ромб и квадрат"

Давайте ещё раз вспомним, что параллелограмм – это четырёхугольник, у которого противоположные стороны попарно параллельны. А прямоугольник – это параллелограмм, у которого все углы прямые.

На этом уроке мы поговорим о таких геометрических фигурах как ромб и квадрат.

Итак, ромб – это параллелограмм, у которого все стороны равны.

Так как ромб является параллелограммом, то он обладает всеми его свойствами, о которых мы с вами говорили на предыдущих уроках.

Теорема. Свойства диагоналей ромба. У ромба диагонали взаимно перпендикулярны и лежат на биссектрисах его углов.

Доказательство.

Рассмотрим .

, следовательно, – медиана.

– равнобедренный.

Медиана – биссектриса, высота.

Следовательно, диагональ и лежит на биссектрисе .

Что и требовалось доказать.

Теперь сформулируем и докажем признаки ромба.

Теорема. Признак ромба. Если у параллелограмма диагонали взаимно перпендикулярны, то этот параллелограмм – ромб.

Доказательство.

Рассмотрим и .

Сторона – общая, , так как диагонали т. делятся пополам

по двум катетам.

Следовательно, .

, .

Следовательно, .

– ромб.

Что и требовалось доказать.

И ещё один признак.

Теорема. Признак ромба. Если у параллелограмма одна из диагоналей лежит на биссектрисе угла, то этот параллелограмм – ромб.

Доказательство.

как накр. лежащие при и секущей .

Следовательно, .

– равнобедренный, то есть .

Следовательно, .

– ромб.

Что и требовалось доказать.

Задача. Чему равны углы ромба, если его меньшая диагональ равна стороне?

– равносторонний.

Ответ: , , , .

Решим ещё одну задачу.

Задача. В ромбе перпендикуляр , проведённый из вершины делит сторону пополам. Найдите градусную меру .

– прямоугольный.

, то есть .

, – внутр. одностор. при и секущей .

Так как , то .

Ответ: .

Теперь поговорим о квадрате.

Квадрат – это прямоугольник, у которого все стороны равны. Также можно сказать, что квадрат – это ромб, у которого все углы прямые.

Эти два определения равносильны. Из каждого следует, что квадрат – это параллелограмм, который одновременно является и прямоугольником, и ромбом.

Следовательно, квадрат обладает всеми свойствами и прямоугольника, и ромба.

Основные свойства квадрата:

1.Все углы квадрата прямые.

2. Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и лежат на биссектрисах его углов.

Задача. На рисунке – квадрат, . Найдите .

, – смежные, то есть .

Так как , то .

– равнобедренный, тогда .

Для учеников 1-11 классов и дошкольников
Бесплатные сертификаты учителям и участникам

ГЕОМЕТРИЯ 8 класс

Ромб. Квадрат

Познавательные: умеют выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки; понимают и используют наглядность в процессе решения задач.

Регулятивные : проявляют познавательный интерес к изучению предмета.

Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками.

Личностные: умеют контролировать процесс и результат учебной математической деятельности

Организация пространства

Формы работы

Фронтальная (Ф); индивидуальная (И); групповая (Г)

Образовательные
ресурсы

• Задания для фронтальной, групповой работы

I этап. Проверка домашнего задания

Выявить трудности, возникшие при выполнении домашнего задания

(Ф) 1. Дайте определение прямоугольника.

2. Перечислите свойства прямоугольника. Докажите одно из них.

3. Перечислите признаки прямоугольника.

4. Решите задачу:

Через середину диагонали KМ прямоугольника KLMN перпендикулярно этой диагонали проведена прямая, пересекающая стороны KL и MN в точках А и В соответственно. Известно, что АВ = ВМ = 6. Найдите бо́льшую сторону прямоугольника.

а) Прямоугольные ∆ МОВ и ∆ KОА равны по катету и прилежащему к нему острому углу ( KО = МО , так как О – середина диагонали KМ ;  BMO =  AKO , как накрест лежащие при параллельных прямых KL и MN и секущей KМ ), тогда АО = ОВ = 3 см ( АВ = 6 см), АK = MB = 6 см.

б) ∆ АМО = ∆ ВМО по двум катетам ( АО = ВО , МО – общая сторона,  AOM =  MOB = 90°), тогда AM = MB = 6 см и ∆ АМВ – равносторонний.

в)  AMO =  BMO = 30°, так как ∆ АМВ – равносторонний, МО – медиана, высота и биссектриса ∆ АМВ .

г)  KLM = 90°,  AMO = 30°,  BMO = 30°, тогда  AML = 30°.

д) ∆ ALM – прямоугольный, в нем  AML = 30°, AM = 6 см, тогда AL = 3 см.

е) АK = 6 см, AL = 3 см, тогда KL = 9 см.

Ответ : KL = 9 см.

5. Решите задачи по готовым чертежам:

1) ABCD – прямоугольник. Найти:  ABF . 2) АСЕK – прямоугольник, ВС = 5 см. Найти: P _BDFM

II этап. Учебно-познавательная деятельность Изучение нового материала

Ввести понятия ромба, квадрата, рассмотреть свойства и признаки этих фигур

(Ф) 1. Введение понятия ромба.

Рисунок и записи на доске и в тетрадях учащихся:

ABCD – ромб, если ABCD – параллелограмм и АВ = ВС = СD = DA .

(Г/Ф) 2. Свойства ромба, признак ромба.

– Перечислите все свойства ромба как частного вида параллелограмма.

Выясните, каким еще свойством обладают диагонали ромба, кроме того, что они точкой пересечения делятся пополам. (Работа в группах с последующим обсуждением свойства диагоналей ромба.)

На доске и в тетрадях записать:

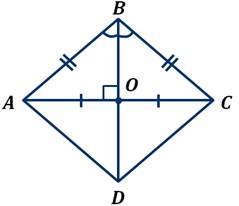
Свойства ромба (рис. 9) :

Если ABCD – ромб, то:

а) АВ = ВС = CD = AD ;

б) АВ || CD , AD || ВС ;

в)  А =  С ,  В =  D ;

г) АО = ОС , ВО = ОD ;

д) АС  ВD .

е) АО , ВО , СО , DО – биссектрисы углов A , B , C , D .

– Сформулируйте утверждение, обратное особому свойству ромба, и выясните его справедливость. (Работа в группах с последующим обсуждением.)

3. Определение квадрата.

ABCD – квадрат, если ABCD – прямоугольник, AB = BC = CD = DA .

4. Свойства квадрата, признаки квадрата.

– Перечислите свойства квадрата, учитывая, что квадрат – это частный случай прямоугольника и ромба. Записать на доске и в тетрадях:

Свойства квадрата:

а) AB = BC = CD = AD ; AB || CD , ВС || AD ;

б)  А =  В =  С =  D = 90°

в) ВО = ОС = ОD = АО , BD  АС , АО , ВО , СО , DO – биссектрисы  A ,  B ,  C ,  D соответственно.

– Сформулируйте признаки квадрата

Закрепление изученного материала

Закрепить полученные знания

(Ф/И) 1. Решить задачу № 406.

Дано: ABCD – ромб,  B = 60°, АС = 10,5 см.

Найти: P _АВСD .

 B = 60°, АВ = ВС (так как АВ и ВС – стороны ромба), тогда  BAC =  BCA =
= 60°, то есть ∆ АВС – равносторонний и АВ = АС = 10,5 см. У ромба все стороны равны, поэтому P _АВСD = 4 · АВ = 4 · 10,5 = 42 (см).

(И) 2. Решить самостоятельно № 407

 ABC = 45°. BD – диагональ и биссектриса  ABC .

 ABD = 45° : 2 = 22°30'

Из ∆ АВО (  O = 90°, так как диагонали ромба перпендикулярны):

Читайте также: