Золотое сечение в акустике реферат
Обновлено: 02.07.2024
Тема расположения акустических систем в комнате для прослушивания претерпевала множество обсуждений и споров. Особо увлеченные люди писали на эту тему доклады и книги, стараясь донести читателю некую универсальную истину, состоящую из многообразия терминов и формул, чертежей и графиков. Одним из таких энтузиастов является основатель фирмы Cardas Audio – Джордж Кардас (George Cardas).
Я ориентируюсь на слух. По этому параметру был выбран весь мой сетап, слухом я пользовался и при выборе места для АС в моей комнате. По большому счету, то положение АС, на котором я остановился, меня вполне устраивало. Периодически, когда хотелось получить от звука чего-то конкретного, я направлял динамики полочников на себя – вокал становится очерченнее и яснее , с более явным позиционированием. Но при этом же несколько теряется масштаб стерео. Когда хочется того самого масштаба – динамики АС смотрят прямо – и вот сцена обретает более крупные очертания, стерео окружает, но позиции инструментов и вокала не так точно локализуются.
Далее, думаю, не будет лишним ознакомить читателя с моей комнатой для прослушивания.
Помещение ничем особенным не отличается от многих других, которые собратья-меломаны приспособили под свое пристанище. Параметры его я укажу на схеме ниже:
АС на стойках я разместил вот так:
При таком расположении, расстояние от фазоинвертора до стены примерно 45 сантиметров. Как можно видеть, между слушателем и АС образовался практически правильный треугольник. Левую колонку смещать ближе к двери опасно – дверь открывается в комнату. Понимаете, какая неприятность может произойти с тем, кто ее откроет.
Заминка с калькулятором вышла в тот момент, когда он попросил у меня расстояние между моими АС. Погоди, Джордж, а не за этим ли я пришел к тебе? Узнать, где и как, да на каком расстоянии?
В моем случае были определены два отрезка: по длинной стене примерно 154 см., по короткой – примерно 120 см.
Отсчитываю рулеткой от угла и первый, и второй. Таким образом формирую прямоугольник, и рисую ему малярным скотчем диагональ. Минуточку, сейчас все станет понятно:
ОЛОТОЕ СЕЧЕНИЕ в музыке - обнаруживающаяся во мн. муз. произв. связь важных особенностей построения целого или его частей с т.н. золотым сечением. Понятие З. с. относится к области геометрии; З. с. называют деление отрезка на две части, при котором целое так относится к большей части, как бОльшая часть к меньшей (гармонич. деление, деление в крайнем и среднем отношении). Если целое обозначить буквой а, бОльшую часть буквой b и меньшую - буквой c, соотношение это выражается пропорцией а:b=b:с. В числовом выражении отношение b:a составляет непрерывную дробь, приближённо равную 0,618034…
Содержание работы
Содержимое работы - 1 файл
Доклад.docx
РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИННОВАЦИОННЫХ ТЕХНОЛОГИЙ И ПРЕДПРИНИМАТЕЛЬСТВА
Пензенский филиал
на тему: Золотое сечение в музыке.
Выполнил: студентки гр.09у1 Гущина А.О. и
Антошкина М.П.
Проверил: старший преподаватель Бубнова Е.М.
Алгебра музыки
Анализ Хроматической фантазии И. С. Баха
ЗОЛОТОЕ СЕЧЕНИЕ в музыке - обнаруживающаяся во мн. муз. произв. связь важных особенностей построения целого или его частей с т.н. золотым сечением. Понятие З. с. относится к области геометрии; З. с. называют деление отрезка на две части, при котором целое так относится к большей части, как бОльшая часть к меньшей (гармонич. деление, деление в крайнем и среднем отношении). Если целое обозначить буквой а, бОльшую часть буквой b и меньшую - буквой c, соотношение это выражается пропорцией а:b=b:с. В числовом выражении отношение b:a составляет непрерывную дробь, приближённо равную 0,618034…
Искусству присуще стремление к стройности, соразмерности, гармонии. Мы находим их в пропорциях архитектуры и скульптуры, в расположении предметов и фигур, сочетании красок в живописи, в чередовании рифм и мерности ритма в поэзии, в последовательности музыкальных звуков. Эти свойства не выдуманы людьми. Они отражают свойства самой природы.
Человек различает окружающие его предметы по форме. Интерес к форме какого-либо предмета может быть продиктован жизненной необходимостью, а может быть вызван красотой формы. Форма, в основе построения которой лежат сочетание симметрии и золотого сечения, способствует наилучшему зрительному восприятию и появлению ощущения красоты и гармонии. Целое всегда состоит из частей, части разной величины находятся в определенном отношении друг к другу и к целому. Принцип золотого сечения – высшее проявление структурного и функционального совершенства целого и его частей в искусстве, науке, технике и природе. Еще в эпоху Возрождения художники открыли, что любая картина имеет определенные точки, невольно приковывающие наше внимание, так называемые зрительные центры. При этом абсолютно неважно, какой формат имеет картина - горизонтальный или вертикальный. Таких точек всего четыре, и расположены они на расстоянии 3/8 и 5/8 от соответствующих краев плоскости. Данное открытие у художников того времени получило название "золотое сечение" картины. Поэтому, для того чтобы привлечь внимание к главному элементу фотографии, необходимо совместить этот элемент с одним из зрительных центров.
В эпоху Возрождения усиливается интерес к золотому делению среди ученых и художников в связи с его применением как в геометрии, так и в искусстве, особенно в архитектуре Леонардо да Винчи, художник и ученый, видел, что у итальянских художников эмпирический опыт большой, а знаний мало. Он задумал и начал писать книгу по геометрии, но в это время появилась книга монаха Луки Пачоли, и Леонардо оставил свою затею. По мнению современников и историков науки, Лука Пачоли был настоящим светилом, величайшим математиком Италии в период между Фибоначчи и Галилеем. Лука Пачоли был учеником художника Пьеро делла Франчески, написавшего две книги, одна из которых называлась “О перспективе в живописи”. Его считают творцом начертательной геометрии.
Лука Пачоли прекрасно понимал значение науки для искусства. В 1496 г по приглашению герцога Моро он приезжает в Милан, где читает лекции по математике. В Милане при дворе Моро в то время работал и Леонардо да Винчи. В 1509 г. в Венеции была издана книга Луки Пачоли “Божественная пропорция” с блестяще выполненными иллюстрациями, ввиду чего полагают, что их сделал Леонардо да Винчи. Книга была восторженным гимном золотой пропорции. Среди многих достоинств золотой пропорции монах Лука Пачоли не преминул назвать и ее “божественную суть” как выражение божественного триединства бог сын, бог отец и бог дух святой (подразумевалось, что малый отрезок есть олицетворение бога сына, больший отрезок – бога отца, а весь отрезок – бога духа святого).
Алгебра музыки.
Очевидно, такое расположение кульминационных моментов музыкальной мелодии является важным элементом ее гармонической композиции, придающим художественную выразительность и эстетическую эмоциональность мелодии.
Характерно, что в некоторых случаях авторы музыкальных произведений смещали их вершину от точки золотого сечения, что придавало мелодиям неустойчивый характер. По мнению Л.Мазеля, это входило в намерения авторов, например, при сочинении скерцо, рондообразных финалов.
По наблюдениям Л.Сабанеева, в музыкальных произведениях различных композиторов обычно констатируется не одно золотое сечение, а целая серия подобных сечений. Каждое такое сечение отражает свое музыкальное событие, качественный скачок в развитии музыкальной темы. В изученных им 1770 сочинениях 42 композиторов наблюдалось 3275 золотых сечений. Количество произведений, в которых наблюдалось хотя бы одно золотое сечение, составило 1338. Наибольшее количество музыкальных произведений, в которых имеется золотое сечение, у Аренского (95%), Бетховена (97%), Гайдна (97%), Моцарта (91%), Скрябина (90%), Шопена (92%), Шуберта (91%).
Наиболее детально были изучены все 27 этюдов Шопена. В них обнаружено 154 золотых сечения; всего в трех этюдах золотое сечение отсутствовало. В некоторых случаях строение музыкального произведения сочетало в себе симметричность и золотое сечение одновременно; в этих случаях оно делилось на несколько симметричных частей, в каждой из которых проявляется золотое сечение. У Бетховена также сочинения делятся на две симметричные части, а внутри каждой из них наблюдаются проявления золотой пропорции.
Характерно, что наиболее часто золотое сечение обнаруживается в произведениях высокохудожественных, принадлежащих гениальным авторам. Может быть, частота проявлений золотой пропорции является одним из объективных критериев оценки гениальности музыкальных произведений и их авторов?
Итак, можно признать, что золотая пропорция является критерием гармонии композиции музыкального произведения.
Анализ Хроматической фантазии И. С. Баха
Хроматическая фантазия написана в размере 4/4, имеет 79 тактов, т. е. 79• 4 = 316 четвертных долей.
Итак, "целое" а=316. Фантазия состоит из двух ясно различимых по характеру частей, отделенных друг от друга паузой. Первая часть, прелюдия, заканчивается на арпеджированном доминантовом трезвучии с разрешением на 2-й четверти 49-го такта, на которой стоит знак ферматы (удлинение звука), и затем идет пауза. Таким образом, первая часть фактически заканчивается на 3-й четверти 49-го такта, т. е. на 195-й (48 • 4 + 3) четверти a1 = 195. На вторую часть приходится 121 четверть (a2 = a − a1 = 316 − 195 = 121).
Вычисляя "теоретическую" длину первой части с помощью коэффициента золотого сечения, мы с поражающей точностью находим
Итак, Хроматическая фантазия разделена на первую и вторую части в золотой пропорции:
Но на этом чудеса гениального творения Баха только начинаются. Построив ряд золотого сечения при а=316, имеем
Каково же должно быть наше удивление, когда мы обнаружим, что на 124-й четверти находится кульминация первой части и стоит знак ферматы •, а на 77-й четверти от начала второй части имеет место кульминация второй части. Таким образом, кульминация обоих частей с небольшой погрешностью, легко объяснимой растяжимостью темпов, делит эти части по закону золотого сечения. Далее, каждый из полученных четырех разделов Хроматической фантазии имеет характерные особенности, которые также с потрясающей точностью приходятся на точки золотого сечения этих разделов. Также Розенов нашел и более мелкие деления Хроматической фантазии в золотой пропорции.
Необходимо сказать, что золотое сечение имеет большое применение в нашей жизни.
Было доказано, что человеческое тело делится в пропорции золотого сечения линией пояса.
Раковина наутилуса закручена подобно золотой спирали.
Благодаря золотому сечению был открыт пояс астероидов между Марсом и
Юпитером – по пропорции там должна находиться ещё одна планета.
Возбуждение струны в точке , делящей её в отношении золотого деления, не вызовет колебаний струны, то есть это точка компенсации.
На летательных аппаратах с электромагнитными источниками энергии создаются прямоугольные ячейки с пропорцией золотого сечения.
1. Д. Пидоу. Геометрия и искусство. – М.: Мир, 1979.
Тема расположения акустических систем в комнате для прослушивания пережила множество обсуждений и споров. Особо увлеченные люди писали на эту тему доклады и книги, стараясь подарить читателю некую универсальную истину в многообразии терминов, формул, чертежей и графиков.
Подготовка
Я ориентируюсь на слух. В соответствии с ним был выбран весь мой сетап, слухом же я пользовался и при выборе места для АС в моей комнате. По большому счету, то положение АС, на котором я остановился, меня вполне устраивало.
Периодически, когда хотелось получить от звука чего-то конкретного, я направлял динамики полочников на себя — вокал становится четче и яснее, с более явным позиционированием. Но при этом несколько теряется масштаб стерео. Когда хочется того самого масштаба, динамики АС смотрят прямо — и тогда сцена обретает более крупные очертания, стерео окружает, но позиции инструментов и вокала не так точно локализуются.
Не лишним будет ознакомить читателя с моей комнатой для прослушивания. Помещение ничем особенным не отличается от многих других, которые собратья-меломаны приспособили под свое пристанище. Его параметры я укажу на схеме ниже:

АС на стойках я разместил вот так:

При таком расположении расстояние от фазоинвертора до стены — примерно 45 сантиметров. Как можно видеть, между слушателем и АС образовался почти правильный треугольник. Смещать левую колонку ближе к двери опасно — дверь открывается в комнату. Понятно, какая неприятность может произойти с тем, кто ее откроет.
В моем случае были определены два отрезка: по длинной стене примерно 154 см, по короткой — примерно 120 см. Отсчитываю рулеткой от угла и первый, и второй. Таким образом формирую прямоугольник и рисую ему малярным скотчем диагональ. Минуточку, сейчас все станет понятно:

Вот и она, заветная диагональ зеленого цвета. Согласно теории, именно на эту диагональ должен быть ориентирован НЧ-драйвер. Располагаться АС могут в любой из точек этой диагонали, соблюдая синхронность левого и правого канала.

Вкратце обосную выбор именно этой позиции: увеличилось расстояние от АС до задней стены, что благоприятно сказалось на построении сцены в глубину. Если сдвинуть АС ближе к центру комнаты — очень страдает ширина сцены. Так что я сел на краешек дивана, и тогда моя голова стала вершиной почти идеального треугольника.
Прослушивание и сравнение
Не претендуя на научный трактат, а лишь ради собственного любопытства, я также провел замеры АЧХ в обеих позициях для АС, и с различным углом их разворота в сторону слушателя. Потому как интересно было сравнить свои субъективные впечатления с графиками, которые я получил по результатам замеров.
Стоит учесть, что представленные мною графики не претендуют на безоговорочную достоверность АЧХ акустических систем в помещении. Но учитывая общую точку отсчета, они все-таки несут информацию о том или ином положении АС в пространстве.
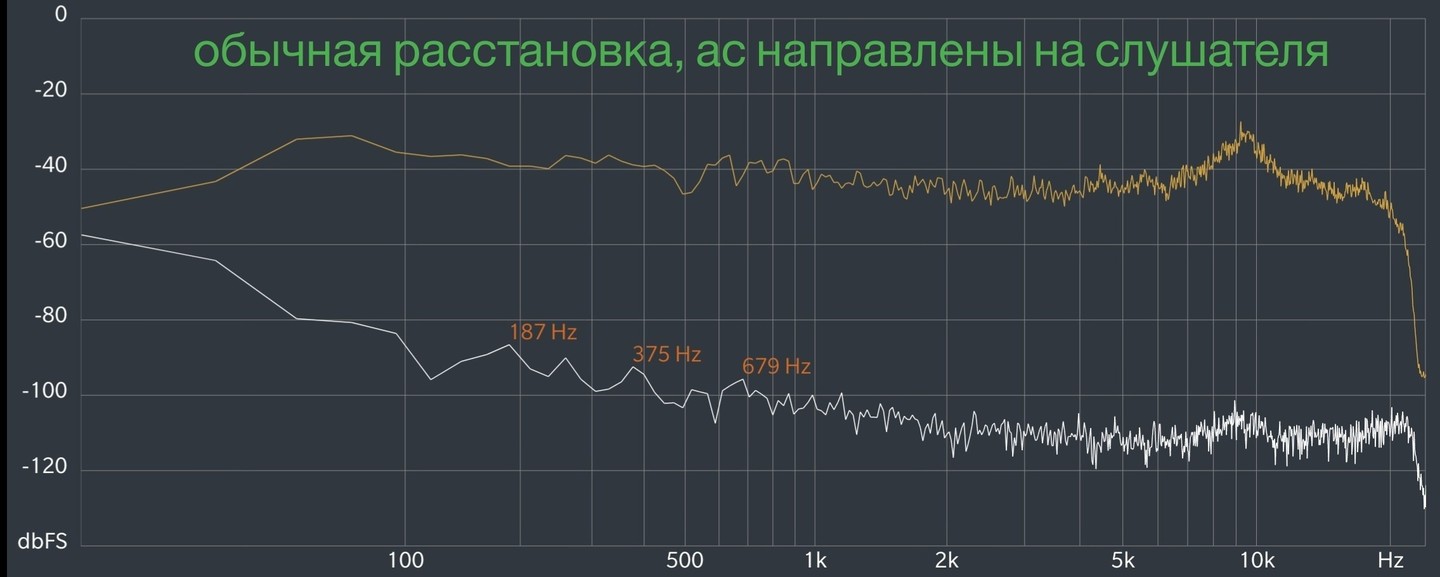
Начнем с привычной мне точки расположения АС. График для нее, полученный на розовом шуме, выглядит вот так:
Рассматриваем пиковую кривую желтого цвета, на белую не обращаем внимания. Для удобства, здесь же размещу следующий график:
Субъективные впечатления совпали с тем, что я увидел на последнем графике: общая картина по НЧ стала восприниматься как более ровная. Схожую ситуацию можно наблюдать и в зоне СЧ/ВЧ. В целом, звуковая картина стала более равномерной.
Но не все так гладко, как хотелось бы. Бас стал гармоничнее, но вместе с тем значительно уменьшился уровень громкости, на котором резонансы комнаты начинают вмешиваться в звучание системы. Если доверять моему слуху и генератору частот, помещение резонирует примерно на 54–56 Гц.
Вечерело. Осмотрев с лоджии опустевшие улицы столицы и вдохнув свежего воздуха, я продолжил эксперимент. Теперь АС стояли, в упор глядя на меня коаксиальными драйверами. Первый замер АЧХ в обычном положении АС, но с разворотом на слушателя:
Касаемо субъективных интерпретаций этого способа прослушивания — вопросов у меня практически не возникло. В области низких частот звучание стало более умеренное по сравнению со стандартной расстановкой.
С увеличением громкости до уровня, который немного больше того, что я использую для длительного прослушивания, резонансы помещения не вмешивались, как в прошлый раз. Воображаемая сцена очертилась и очень уверенно демонстрировала позиции всех инструментов и вокалистов. Пожалуй, было даже ощущение излишней концентрации информации в пространстве между акустикой.
Мне кажется, что опыт прослушивания АС в среднем/дальнем поле вносит свои корректировки и требования, которые не применимы к прослушиванию в ближнем поле.
Выводы
Был ли такой опыт полезен? Несомненно! Оставил ли я акустику в точках по золотому сечению? Нет. И на то есть ряд причин, которые я, собственно, уже описал выше. Ориентируясь на рассчитанные точки, в своем помещении я получил конфигурацию, которая вынуждает меня к прослушиванию в практически ближнем поле. А мне масштаб да размах подавай, чтобы аж УХ!
Думаю, что данная теория справедливо заслуживает внимания, и однажды, когда впечатления улягутся, я проведу повторные испытания в комнате с другими параметрами.
- Для учеников 1-11 классов и дошкольников
- Бесплатные сертификаты учителям и участникам
МБОУ СОШ №3 им. К.А.Москаленко
Реферат по математике
Авторы: Межов Илья Сергеевич,
Банных Даниил Дмитриевич
МБОУ СОШ№3 6В класс
Научный руководитель: Чеботарева Марина Викторовна
При подготовке к данному реферату мы изучили много научной литературы не только по математике, но и использовали информацию из других наук: биологии, истории, анатомии. Для начала мы бы хотели привести пример из практики.
Если вы подходите к пустой скамейке и садитесь на неё, то вы сядете не посередине скамейки и, конечно, не на самый край. Если вы незаметно замерите длины, на которые своим телом разделили скамейку, то обнаружите, что отношение большего отрезка к меньшему равно отношению всей длины к большему отрезку. Это число, называется золотым сечением.
Золотое сечение – это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему.
с: b = b: а или a: b = b: c. Первое отношение приблизительно равно 1.6, а второе- 0.6.

Принято считать, что понятие о золотом сечении ввел в научный обиход Пифагор, древнегреческий философ и математик (VI в. до н.э.). Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян.
Золотое отношение обычно обозначают буквой F – прописной буквой греческого алфавита. Такое обозначение принято в честь древнегреческого скульптора Фидия, жившего в V в. до н.э. Он руководил строительством храма Парфенон в Афинах ; в пропорциях этого храма многократно присутствует число F . Его фасад вписывается в прямоугольник, отношение сторон которого равно F .
2. Пентаграмма


Звездчатый пятиугольник называется пентаграммой. Пифагорейцы выбрали пятиконечную звезду в качестве талисмана.

Она считалась символом здоровья и служила опознавательным знаком. Для построения пентаграммы необходимо построить правильный пятиугольник. Способ его построения разработал немецкий живописец и график Альбрехт Дюрер.
Пусть O – центр окружности, A – точка на окружности и Е – середина отрезка ОА. Перпендикуляр к радиусу ОА, восставленный в точке О, пересекается с окружностью в точке D. Пользуясь циркулем, отложим на диаметре отрезок CE = ED. Длина стороны вписанного в окружность правильного пятиугольника равна DC. Откладываем на окружности отрезки, равные DC и получим пять точек для начертания правильного пятиугольника. Соединяем углы пятиугольника через один диагоналями и получаем пентаграмму. Все диагонали пятиугольника делят друг друга на отрезки, связанные между собой золотой пропорцией.
Интересно, что стороны пентаграммы, пересекаясь, образуют снова правильный пятиугольник, в котором пересечение диагоналей даёт нам новую пентаграмму и так далее до бесконечности.
Пентаграмма очень красива, недаром её помешают на свои флаги и гербы многие страны. На флагах многих государств изображена правильная пятиконечная звезда.
Леонардо да Винчи
Также портрет Джоконды долгие годы привлекает внимание исследователей, которые обнаружили, что композиция рисунка основана на золотых треугольниках, являющихся частями правильного звездчатого пятиугольника.




В древнерусском искусстве существовал канон пропорций, позволявший гармонично “вписывать” произведения живописи в интерьер храма. “Троица” - самая совершенная среди сохранившихся икон Андрея Рублева и самое прекрасное творение древнерусской живописи–была, Написана мастером в первой четверти ХV столетия .
Пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона якобы свидетельствуют, что египетские мастера пользовались соотношениями золотого сечения при их создании.

Одним из красивейших произведений древнегреческой архитектуры является Парфенон( V в. до н. э.)-храм Афины. Размеры Парфенона хорошо изучены. Известно, что фасад Парфенона вписан в прямоугольник со сторонами 1:2.
древности является Пантеон.


Знаменитый русский архитектор М. Ф. Казаков широко использовал в своем творчестве золотое сечение. Его талант был многогранным, но в большей степени он проявился в многочисленных проектах жилых домов и усадеб. Например, золотое сечение можно встретить в архитектуре здания бывшего сената в Кремле.
Дом Пашкова Здание сената в Кремле

Еще один архитектурный шедевр Москвы - дом Пашкова - является одним из наиболее совершенных произведений архитектора В.Баженова. Наружный вид дома сохранился почти без изменений до наших дней, несмотря на то, что он сильно обгорел в 1812 году. Многие высказывания зодчего заслуживают внимания. О своем любимом искусстве Баженов говорил: "Архитектура - главнейшие имеет три предмета: красоту, спокойствие и прочность здания. К достижению сего служит руководством знание пропорции, перспективы, механики или вообще физики, а всем им общим вождем является рассудок".
Храм Василия Блаженного


Изучая архитектуру церкви Покрова на Нерли, русский архитектор Шевелев пришел к выводу, что в этом шедевре архитектуры проявляется пропорция, которая представляет собой отношение большей стороны к диагонали прямоугольника с отношением сторон 1:2. Таким образом, в основе взаимосвязанных пропорций этого архитектурного сооружения положены пропорции прямоугольника и его производная – золотая пропорция. Наличие этих пропорций и определило красоту храма.
Галилео Галилей
Если внимательно рассмотреть веточку с листьями, то можно заметить, что основание черешков располагаются по винтовой линии, каждый следующий лист прикреплен выше и в сторону от предыдущего, то есть располагаются по спирали.
В биологических исследованиях 70-90 гг. показано, что, начиная с вирусов и растений и кончая организмом человека, всюду выявляется золотая пропорция, характеризующая соразмерность и гармоничность их строения. Золотое сечение признано универсальным законом живых систем.
Раковина закручена по спирали. Если ее развернуть, то получается длина, немного уступающая длине змеи. Небольшая десятисантиметровая раковина имеет спираль длиной 35 см. Спирали очень распространены в природе. Представление о золотом сечении будет неполным, если не сказать о спирали.

Форма спирально завитой раковины привлекла внимание Архимеда. Он изучал ее и вывел уравнение спирали. Спираль, вычерченная по этому уравнению, называется его именем. Увеличение ее шага всегда равномерно. В настоящее время спираль Архимеда широко применяется в технике.
Винтообразное и спиралевидное расположение листьев на ветках деревьев подметили давно. Спираль увидели в расположении семян подсолнечника, в шишках сосны, ананасах, кактусах и т.д. Совместная работа ботаников и математиков пролила свет на эти удивительные явления природы. Выяснилось, что в расположении листьев на ветке (филотаксис), семян подсолнечника, шишек сосны проявляет себя закон золотого сечения.


Муниципальное общеобразовательное учреждение
Золотое сечение
Выполнил: Арефьев Максим
Руководитель: Копылова Нина Павловна

Содержание
Введение. Пропорции золотого сечения. Ф и φ……………………………………….с.3-4
Глава 1. История золотого сечения…………………………………………………….с.4-7
Глава 2. Построение пропорции………………………………………………………..с.7-8
Глава 4.1. Золотой прямоугольник…………………………………………………. с.9-10
Глава 4.2. Золотой треугольник…………………………………………………. с.10-11
Глава 4.3. Золотой пятиугольник. Построение Евклида…………………………. с.11-12
Глава 4.4. Спираль Архимеда…………………………………………………………. с.13
Глава 6. Золотое сечение в искусстве………………………………………………с.17-18
Глава 6.1. Золотое сечение в живописи………………………………………………. с.17
Глава 6.2. Пирамиды золотого сечения………………………………………………. с.18
Список используемой литературы……………………………………………………. с.20
Пропорция золотого сечения. Ф и φ.
"Геометрия обладает двумя великими сокровищами. Первое - это теорема Пифагора, второе - деления отрезка в крайнем и среднем отношении"
Правильные многоугольники привлекали внимание древнегреческих учёных ещё задолго да Архимеда. Пифагорейцы, выбравшие эмблемой своего союза пентаграмму - пятиконечную звезду, придавали очень большое значение задаче о делении окружности на равные части, то есть о построении правильного вписанного многоугольника. Альбрехт Дюрер (1471-1527гг), ставший олицетворением Возрождения в Германии приводит теоретически точный способ построения правильного пятиугольника, заимствованный из великого сочинения Птолемея "Альмагест".
Интерес Дюрера к построению правильных многоугольников отражает использование их в Средние века в арабских и готических орнаментах, а после изобретения огнестрельного оружия - в планировке крепостей.
Средневековые способы построения правильных многоугольников носили приближенный характер, но были (или не могли не быть) простыми: предпочтение отдавалось способам построения, не требующим даже изменять раствор циркуля. Леонардо да Винчи также много писал о многоугольниках, но именно Дюрер, а не Леонардо, передал средневековые способы построения потомкам. Дюрер, конечно, был знаком с " Началами" Евклида, но не привел в своем "Руководстве к измерению" (о построениях при помощи циркуля и линейки) предложенный Евклидом способ построения правильного пятиугольника, теоретически точный, как и все евклидовы построения. Евклид не пытается разделить заданную дугу окружности на три равные части, и Дюрер знал, хотя доказательство было найдено лишь в XIX веке, что эта задача неразрешима.
Предложенное Евклидом построение правильного пятиугольника включает в себя деление отрезка прямой в среднем и крайнем отношении, названное впоследствии золотым сечением и привлекавшим к себе внимание художников и архитекторов на протяжении нескольких столетий.
Точка В делит отрезок АВЕ в среднем и крайнем отношении или образует золотое сечение, если отношение большей части отрезка к меньшей равно отношению всего отрезка к большей части.
Записанное в виде равенства отношений золотое сечение имеет вид:
Если положить АВ=а, а ВЕ=а/Ф так, чтобы золотое отношение было равно АВ/ВЕ=Ф, то получается соотношение
То есть Ф удовлетворяет уравнению
Это уравнение имеет один положительный корень
Заметим, что 1/Ф = (√5 -1 )/2, так как (√5-1)(√5+1) =5-1=4. За 1/Ф принято считать φ=0.618034….
Ф и φ - прописная и строчная формы греческой буквы "фи".
Такое обозначение принято в честь древнегреческого скульптора Фидия (V век до н. э.) Фидий руководил строительством храма Парфенон в Афинах. В пропорциях этого храма многократно присутствует число φ .
1.История золотого сечения.
Принято считать, что понятие о золотом делении ввел в научный обиход Пифагор, древнегреческий философ и математик (VI в. до н.э.). Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании. Французский архитектор Ле Корбюзье нашел, что в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамсеса, пропорции фигур соответствуют величинам золотого деления. Зодчий Хесира, изображенный на рельефе деревянной доски из гробницы его имени, держит в руках измерительные инструменты, в которых зафиксированы пропорции золотого деления.
Греки же были искусными геометрами. Даже арифметике обучали своих детей при помощи геометрических фигур. Квадрат Пифагора и диагональ этого квадрата были основанием для построения динамических прямоугольников (пр. 1*)
Платон (427. 347гг. до н.э.) также знал о золотом делении. Его диалог "Тимей" посвящен математическим и эстетическим воззрениям школы Пифагора и, в частности, вопросам золотого деления.
В дошедшей до нас античной литературе золотое деление впервые упоминается в "Началах" Евклида. Во 2-й книге "Начал" дается геометрическое построение золотого деления. После Евклида исследованием золотого деления занимались Гипсикл (II в. до н.э.), Папп (III в. н.э.) и др.. В средневековой Европе с золотым делением познакомились по арабским переводам "Начал" Евклида. Переводчик Дж. Кампано из Наварры (III в.) сделал к переводу комментарии. Секреты золотого деления ревностно оберегались, хранились в строгой тайне. Они были известны только посвященным.
В эпоху Возрождения усиливается интерес к золотому делению среди ученых и художников в связи с его применением, как в геометрии, так и в искусстве, особенно в архитектуре. Леонардо да Винчи (пр. 4), художник и ученый, видел, что в итальянских художниках большой эмпирический опыт, но недостаток знаний. Он задумал и начал писать книгу по геометрии, но в это время появилась книга монаха Луки Пачоли, и Леонардо оставил свою затею. По мнению современников и историков науки, Лука Пачоли был настоящим светилом, величайшим математиком Италии в период между Фибоначчи и Галилеем.
Лука Пачоли прекрасно понимал значение науки для искусства. В 1496 г по приглашению герцога Моро он приезжает в Милан, где читает лекции по математике. В Милане при дворе Моро в то время работал и Леонардо да Винчи. В 1509г. в Венеции была издана книга Луки Пачоли "Божественная пропорция" с блестяще выполненными иллюстрациями, ввиду чего полагают, что их сделал Леонардо да Винчи. Книга была восторженным гимном золотой пропорции. Среди многих достоинств золотой пропорции монах Лука Пачоли не преминул назвать и ее "божественную суть" как выражение божественного триединства: бог сын, бог отец и бог дух святой (подразумевалось, что малый отрезок есть олицетворение бога сына, больший отрезок - бога отца, а весь отрезок - бога духа святого).
Леонардо да Винчи также много внимания уделял изучению золотого деления. Он производил сечения стереометрического тела, образованного правильными пятиугольниками, и каждый раз получал прямоугольники с отношениями сторон в золотом делении. Поэтому он дал этому делению название золотое сечение. Так оно и держится до сих пор как самое популярное.
В то же время на севере Европы, в Германии, над теми же проблемами трудился Альбрехт Дюрер. Он делает наброски введения к первому варианту трактата о пропорциях. Дюрер пишет: "Необходимо, чтобы тот, кто что-либо умеет, обучил этому других, которые в этом нуждаются. Это я и вознамерился сделать".
Судя по одному из писем Дюрера, он встречался с Лукой Пачоли во время пребывания в Италии. Альбрехт Дюрер подробно разрабатывает теорию пропорций человеческого тела. Важное место в своей системе соотношений Дюрер отводил золотому сечению. Рост человека делится в золотых пропорциях линией пояса, а также линией, проведенной через кончики средних пальцев опущенных рук, нижняя часть лица - ртом и т.д. Известен пропорциональный циркуль Дюрера.
Построение ряда отрезков золотой пропорции можно производить как в сторону увеличения (возрастающий ряд), так и в сторону уменьшения (нисходящий ряд).
Если на прямой произвольной длины, отложить отрезок m(φ), рядом откладываем отрезок M. На основании этих двух отрезков выстраиваем шкалу отрезков золотой пропорции восходящего и нисходящего рядов .

В последующие века правило золотой пропорции превратилось в академический канон и, когда со временем в искусстве началась борьба с академической рутиной, в пылу борьбы "вместе с водой выплеснули и ребенка". Вновь "открыто" золотое сечение было в середине XIX в. В 1855г. немецкий исследователь золотого сечения профессор Цейзинг опубликовал свой труд "Эстетические исследования". С Цейзингом произошло именно то, что и должно было неминуемо произойти с исследователем, который рассматривает явление как таковое, без связи с другими явлениями. Он абсолютизировал пропорцию золотого сечения, объявив ее универсальной для всех явлений природы и искусства. У Цейзинга были многочисленные последователи, но были и противники, которые объявили его учение о пропорциях "математической эстетикой".

Здесь приводится построение точки Е, делящий отрезок прямой в пропорции золотое сечение.
Из точки В восстанавливается перпендикуляр, равный половине АВ. Полученная точка С соединяется линией с точкой А. На полученной линии откладывается отрезок ВС, заканчивающийся точкой D. Отрезок AD переносится на прямую АВ. Полученная при этом точка Е делит отрезок АВ в соотношении золотой пропорции.
Именно эти отрезки использовал Евклид при построении правильного пятиугольника, т.к. каждая из сторон пятиугольной звезды делится другими именно в такой пропорции.
Звездчатый пятиугольник называется пентаграммой. Пифагорейцы выбрали пятиконечную звезду в качестве талисмана, она считалась символом здоровья и служила опознавательным знаком.
3.Второе золотое сечение.
Такая пропорция обнаружена в архитектуре, а также имеет место при построении композиций изображений удлиненного горизонтального формата.
Построение второго золотого сечения
Деление осуществляется следующим образом. Отрезок АВ делится в пропорции золотого сечения. Из точки С восставляется перпендикуляр СD. Радиусом АВ находится точка D, которая соединяется линией с точкой А. Прямой угол АСD делится пополам. Из точки С проводится линия до пересечения с линией AD. Точка Е делит отрезок AD в отношении 56:44.
На рисунке показано положение линии второго золотого сечения. Она находится посередине между линией золотого сечения и средней линией прямоугольника.

Деление прямоугольника линией второго золотого сечения.
Таким образом было доказано, что разделить отрезок в крайнем и среднем отношении можно не единственным способом.
4. "Золотые" фигуры.
Если построить квадрат со стороной АВ=а, найти середину М отрезка АВ и провести дугу окружности радиусом МС с центром в точке М до пересечения с продолжением стороны АВ в точке Е, то точка В разделит отрезок АЕ в крайнем и среднем отношении.
Чтобы убедиться в этом, заметим, что по теореме Пифагора:
Прямоугольник АЕFD со сторонами АЕ=φАD называется золотым прямоугольником. Четырехугольник АВСD - квадрат. Нетрудно видеть, что прямоугольник ВЕFС также золотой, поскольку BC=a=φВЕ. Это обстоятельство сразу наводит на мысль о дальнейшем разбиении прямоугольника ВЕFС.
Можно ли считать, что прямоугольник с отношением сторон, равным φ, выглядит изящнее, чем прямоугольники с отношением сторон, скажем, 2:1, 3:2 или 5:7. Чтобы ответить на этот вопрос, были проведены специальные эксперименты. Результаты их не вполне убедительны, но все же свидетельствуют о некотором предпочтении, отдаваемом золотому сечению. Впрочем, может ли прямоугольник сам по себе быть захватывающе прекрасным или отталкивающе безобразным?

4.3. Золотой пятиугольник. Построение Евклида.

Построение правильного пятиугольника и пентаграммы.
Для построения пентаграммы необходимо построить правильный пятиугольник.
Пусть О - центр окружности, А - точка на окружности и Е - середина отрезка ОА. Перпендикуляр к радиусу ОА, восстановленный в точке О, пересекается с окружностью в точке D. Пользуясь циркулем, отложим на диаметре отрезок CE = ED. Длина стороны вписанного в окружность правильного пятиугольника равна DC. Откладываем на окружности отрезки DC и получим пять точек для начертания правильного пятиугольника. Соединяем углы пятиугольника через один диагоналями и получаем пентаграмму. Все диагонали пятиугольника делят друг друга на отрезки, связанные между собой золотой пропорцией.
Каждый конец пятиугольной звезды представляет собой золотой треугольник. Его стороны образуют угол 36° при вершине, а основание, отложенное на боковую сторону, делит ее в пропорции золотого сечения.
Есть и золотой кубоид- это прямоугольный параллелепипед с ребрами, имеющими длины 1.618, 1 и 0.618.
Посмотрим теперь, как Евклид использует золотое сечение для того, чтобы построить угол в 72 градуса – именно под таким углом видна сторона правильного пятиугольника из центра описанной окружности. Начнем с отрезка АВЕ, разделенного в среднем и крайнем отношении точкой В. Проведем далее дуги окружностей с центрами в точках В и Е и радиусах АВ, пересекающиеся в точке С. Чуть ниже докажем, что АС=АЕ, а пока примем это на веру.
Итак, пусть АС=АЕ. Обозначим через a равные углы ЕВС и СЕВ. Так как АС=АЕ, то угол АСЕ также равен a. Теорема о том, что сумма углов треугольника равна 180 градусов, позволяет найти угол ВСЕ: он равен 180-2a, а угол ЕАС - 3a - 180. Но тогда угол АВС равен 180-a. Суммируя углы треугольника АВС получаем,
180=(3a -180) + (3a-180) + (180 - a)
Откуда 5a=360, значит a=72.
Итак, каждый из углов при основании треугольника ВЕС вдвое больше угла при вершине, равного 36 градусов. Следовательно, чтобы построить правильный пятиугольник, необходимо лишь провести любую окружность с центром в точке Е, пересекающую ЕС в точке Х и сторону ЕВ в точке Y: отрезок XY служит одной из сторон вписанного в окружность правильного пятиугольника; Обойдя вокруг всей окружности, можно найти и все остальные стороны.
Докажем теперь, что АС=АЕ. Предположим, что вершина С соединена отрезком прямой с серединой N отрезка ВЕ. Заметим, что поскольку СВ=СЕ, то угол СNЕ прямой. По теореме Пифагора:
CN2 = а2 – (а/2j) 2= а2 (1-4j 2)
Отсюда имеем (АС/а) 2 = (1+1/2j) 2 + (1-1/4j 2) = 2+1/j = 1 + j =j 2
Итак, АС = jа = jАВ = АЕ, что и требовалось доказать
Последовательно отсекая от золотых прямоугольников квадраты до бесконечности, каждый раз соединяя противоположные точки четвертью окружности, мы получим довольно изящную кривую. Первым внимание на неё обратил древнегреческий ученый Архимед (пр.5), имя которого она и носит. Он изучал её и вывел уравнение этой спирали.


В настоящее время спираль Архимеда широко используется в технике.
С золотым сечением косвенно связано имя итальянского математика Леонардо из Пизы, который известен больше по своему прозвищу Фибоначчи (Fibonacci - сокращенное filius Bonacci, то есть сын Боначчи).
В 1202г. им была написана книга "Liber abacci", то есть "Книга об абаке" . "Liber abacci" представляет собой объемистый труд, содержащий почти все арифметические и алгебраические сведения того времени и сыгравший заметную роль в развитии математики в Западной Европе в течение нескольких следующих столетий. В частности, именно по этой книге европейцы познакомились с индусскими ("арабскими") цифрами.
Сообщаемый в книге материал поясняется на большом числе задач, составляющих значительную часть этого трактата.
Рассмотрим одну такую задачу:
"Сколько пар кроликов в один год от одной пары рождается?
Некто поместил пару кроликов в некоем месте, огороженном со всех сторон стеной, дабы узнать, сколько пар кроликов родится в течение этого года, если природа кроликов такова, что через месяц пара кроликов воспроизведет другую, а рождают кролики со второго месяца после своего рождения"
Читайте также: