Теорема о трех перпендикулярах реферат

Обновлено: 05.07.2024

2 Автор проекта : учащиеся 10 а класса Руководитель : Долгополова С.И. – учитель первой квалификационной категории

3 Цели проекта : Собрать информацию об истории теоремы о трех перпендикулярах Найти различные способы доказательства теоремы о трех перпендикулярах Найти примеры использования этой теоремы для доказательства различных свойств геометрических фигур Привести примеры решения различных задач с использованием этой теоремы

4 Этапы работы над проектом Формирование групп для работы над различными вопросами проекта Сбор и изучение информации группами

5 Форма представления результатов Выступление каждой группы с подготовленными вопросами на уроке геометрии Подготовка презентации проекта(обобщение материала всех групп) Выставление данной работы на школьный сайт Защита работы на школьной научно-практической конференции

6 Содержание Литература Из истории доказательства теоремы о трех перпендикулярах Различные способы доказательства теоремы Применение теоремы для доказательства различных свойств пространственных фигур Свойство диагонали куба Свойство ребер тетраэдра Различные задачи, в решении которых применяется теорема о трех перпендикулярах

7 Литература Глейзер Г.И. История математики в школе 9-10 классы/Г.И. Глейзер.-М.:Просвещение, Болгарский Б.В. Очерки по истории математики. Стройк Д.А. Краткий очерк истории математики, 1984 Белл Б.В. Очерки по истории математики. Книга для учителя – пер. с английского –М. Просвещение Интернет ресурсы.

8 Из истории доказательства теоремы о трех перпендикулярах

10 Восточный вариант: Насир ад-Дин ат-Туси Дата рождения:18 февраля 18 февраля Место рождения:Тус Дата смерти:26 июня 26 июня 1274 (73 года)1274 Место смерти:Марага Научная сфера: астрономия, математика, философия, география, музыка, оптика, медицина, минералогия математика философия география музыка оптика медицина минералогия

11 Биография (Насир ад-Дин Абу Джа`фар Мухаммад ибн Мухаммад ат-Туси) арабский математик и астроном. Персидский математик, механик и астроном XIII века, ученик Камал ад-Дина ибн Юниса, чрезвычайно разносторонний учёный, автор сочинений по философии, географии, музыке, оптике, медицине, минералогии. Был знатоком греческой науки, комментировал труды Евклида, Архимеда, Автолика, Феодосия, Менелая, Аполлония, Аристарха, Гипсикла, Птолемея.

17 Формулировка теоремы Бертраном Бертран сформулировал ее так: Пусть прямая АР перпендикулярна Q, а точка Р –ее основание и пусть ВС- произвольная прямая этой плоскости. Проведем из точки Р прямую PD перпендикулярно ВС и соединим точки А и D; тогда прямая АD тоже будет перпендикулярна к ВС.

18 Европейский вариант Бертран Жан Луи Дата рождения: 1731 Дата смерти: 1812 Страна: Швейцария

20 Различные способы доказательства теоремы о трех перпендикулярах

21 Формулировка теоремы Прямая, проведённая в плоскости через основание наклонной перпендикулярно к её проекции на эту плоскость, перпендикулярна и к самой наклонной

23 Второе доказательство Доказательство. 1) СD ·CA = CD ·(CB+BA)=CD ·CB+CD ·BA 2) По условию CD CB. Значит, CD ·CB=0; CD BA, значит СD ·BA=0. Таким образом получаем: CD·CA=0,CD CA, c AC

24 Третье доказательство Обратимся к рисунку, на котором отрезок АВ – перпендикуляр к плоскости π, АС – наклонная, m – прямая, проведенная в плоскости π через точку С перпендикулярно к проекции СВ наклонной. Докажем, что m перпендикулярна АС. Рассмотрим плоскость АСВ. Прямая m перпендикулярна к этой плоскости, так как она перпендикулярна к двум пересекающимся прямым АВ и ВС, лежащим в плоскости АСВ (m ВС по π). Отсюда следует, что прямая m перпендикулярна к любой прямой, лежащей в плоскости АВС, в частности m перпендикулярна АС. Теорема доказана.

25 Четвертое доказательство От точки А отложим равные отрезки: АМ= АN. Точки М и N соединим с точками O и S. В ОА есть одновременно высота и медиана, этот треугольник равнобедренный: ОМ = ОN. Прямоугольные треугольники OSM и OSN равны (по двум катетам). Из их равенства следует, что SM= SN и SA- медиана равнобедренного треугольника MSN. Значит, SA одновременно и высота этого треугольника, т. е. SAMN.

26 Пятое доказательство 3 способ доказательства теоремы о трех перпендикулярах. На прямой t возьмем произвольную точку В и соединим ее с точками О и S. Из прямоугольных треугольников SOB, SOA и AOB: = SO 2 + OB 2, SA 2 = =SO 2 + OA 2, OB 2 - OA 2 = AB 2. Вычтя из первого равенства второе, получим:SB 2 – SA 2 = =OB 2 – OA 2. Приняв во внимание третье равенство, будем иметь: SB 2 – SA 2 = AB 2, SB 2 = SA 2 +AB 2. Согласно теореме, обратной теореме Пифагора, SAAB, т. е. tSA

27 Применение теоремы о трех перпендикулярах для доказательства свойств элементов различных пространственных фигур

28 О диагонали куба

29 О ребрах тетраэдра

30 Различные задачи Текстовые задачи, требующие при решении использования теоремы о трех перпендикулярах

Теоремы о трех перпендикулярах — фундаментальные теоремы геометрии и стереометрии в частности. Стереометрия — часть геометрии, изучающая объемные фигуры в пространстве.

Прямая a, принадлежащая плоскости γ, проведенная через основание наклонной b и перпендикулярная ее проекции c на эту плоскость, перпендикулярна и наклонной b.

Доказательство:

Пусть b — наклонная к плоскости γ, c — ее проекция, A — точка пересечения b и γ, a — прямая в плоскости γ, проходящая через A и перпендикулярная c, d перпендикулярна γ.

Проведем прямую e параллельно d. Прямая e параллельна d, а d перпендикулярна γ.

Следовательно: e также перпендикулярна γ и прямой a, лежащей в этой плоскости.

Параллельные прямые e и d задают плоскость β (параллельные прямые определяют плоскость, причем только одну). При этом a перпендикулярна пересекающимся прямым e и d — как следствие, она перпендикулярна и плоскости β.

Это значит, что a перпендикулярна и любой прямой в этой плоскости, в том числе и b.

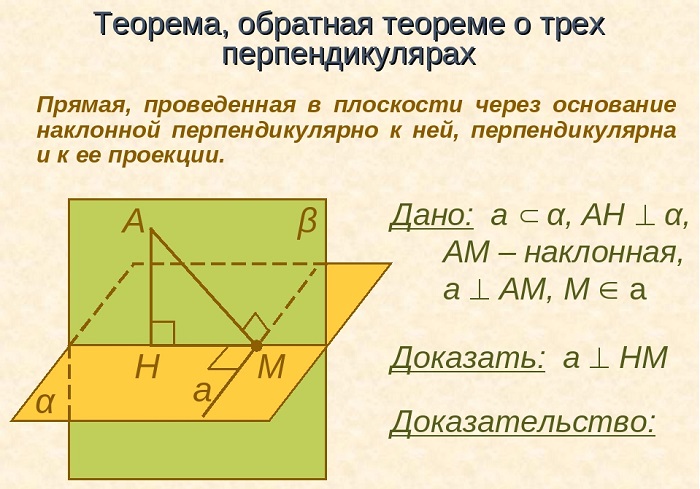
Теорема, обратная теореме о трех перпендикулярах

Верна и обратная теорема.

Лежащая в плоскости γ прямая a, проведенная через основание наклонной b и перпендикулярная ей, будет перпендикулярна и ее проекции на данную плоскость.

Доказательство:

Аналогично объяснение обратной теоремы о трех перпендикулярах.

Через точку А проведем прямую e. Заметим, что e||d и e⊥γ — следовательно, e⊥a, так как a∈γ.

Две прямые e и d определяют плоскость β. При этом a перпендикулярна двум пересекающимся прямым e и b, лежащим в плоскости β.

Отсюда следует, что a перпендикулярна плоскости β и a⊥c, так как c∈β.

В таком виде эти теоремы даются в школьных учебниках, но прохождение прямой через основание наклонной — не является обязательным условием.

Более короткая и простая формулировка теорем:

Лежащая в плоскости прямая будет перпендикулярна наклонной к данной плоскости, если она перпендикулярна проекции этой наклонной.
Прямая, лежащая в плоскости и перпендикулярная наклонной, будет перпендикулярна и проекции наклонной на плоскость.

Если прямая не проходит через основание наклонной, то прямая и наклонная будут скрещиваться, а прямая и проекция наклонной — пересекаться.

Примеры решения задач

Теоремы о трех перпендикулярах имеют широкое применение. Ниже приведены готовые решения задач для учащихся 10 класса, которые помогут как в самостоятельной работе, так и на уроке.

Дано: равносторонний треугольник АBC, отрезок BD перпендикулярен плоскости АB и BC, BE — биссектриса угла АBC.

Найти: угол между DE и AC.

Решение:

на чертеже изобразим ΔАBC, биссектрису BE и отрезок BD.

BD перпендикулярен плоскости АBC, следовательно: BD||BE, так как BE∈АBC.

ΔАBC равносторонний, биссектриса BE является одновременно и высотой, BE перпендикулярен АC. Согласно теореме о трех перпендикулярах, ∠DEC=90°.

Дано: тетраэдр ABCD.

Найти: угол между скрещивающимися ребрами тетраэдра.

Решение:

BO — высота тетраэдра, падает на пересечение медиан ΔACD.

Так как ΔACD равносторонний, медиана АО является одновременно его высотой, АО⊥CD.

В соответствии с теоремой о трех перпендикулярах AB — наклонная к плоскости ACD, AO — ее проекция.

Одним из важных утверждений стереометрии (так называется геометрия в пространстве) является теорема о трёх перпендикулярах.

Она помогает при нахождении прямых углов, сведении задачи к применению теоремы Пифагора и тригонометрических функций, что в целом значительно упрощает вычислительную работу.

Формулировка теоремы о трёх перпендикулярах

Прямая, проведённая на плоскости через основание наклонной перпендикулярно её проекции, перпендикулярна и к самой наклонной.

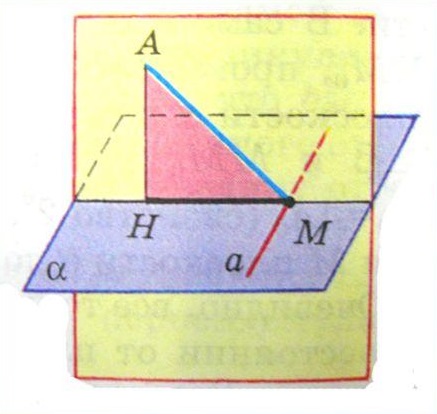
Доказательство теоремы

Существуют принципиально различные методы.

Первый метод

Основан на равенстве наклонных при равных проекциях.

Проведя к плоскости α отрезок AB, AB ⊥ α, B ∈ α через точку A_AC, C ∈ α, b ⊥ BC, C ∈ b, b ⊂ α, возникает необходимость убедиться, что b ⊥ AC.

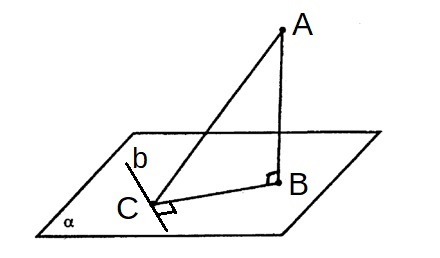
От C на прямой b откладывают равные отрезки CD, CE, затем соединяют точки D; E с B, A.

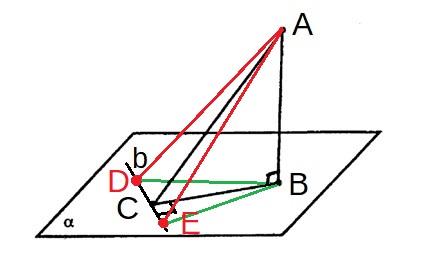
Поскольку CD, CE равны по построению, b ⊥ BC, BC - общий катет, то треугольники ΔBCD, ΔBCE, являющиеся прямоугольными, равны. Следовательно, BD = BE.

Из полученного условия вытекает равенство наклонных AD, AE (lkz rjnjhs[ BD, BE – проекции). Поэтому ΔAED является равнобедренным.

По построению CD = CE, откуда следует искомая перпендикулярность прямых AC и b.

Второй метод

Основан на определении, свойствах, признаках перпендикулярности прямой и плоскости.

AB и b – скрещивающиеся. BC – их общий перпендикуляр, AC – наклонная к α.

Проводя FC параллельно AB, получают FC ⊥ α.

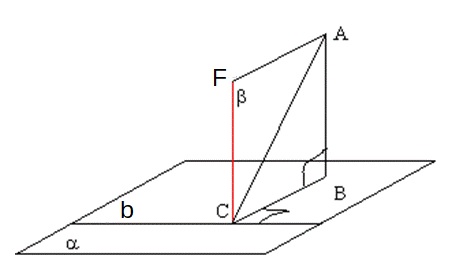
Так как по условию b ⊥ AC, по построению b ⊥ FC, то b ⊥ ACF.

Из того, что C ∈ ACF, A ∈ ACF, следует, что AC ⊂ ACF, отсюда b ⊥ AC.

Теорема, обратная теореме о трёх перпендикулярах

Меняя местами понятия проекции и наклонной, получают взаимно обратное утверждение:

Если прямая, проведённая в плоскости через основание наклонной, перпендикулярна наклонной, то она перпендикулярна и её проекции.

Доказательства аналогичны уже приведённым ранее.

Решение задач на применение теоремы

Класс заданий, связанных с использованием рассматриваемого материала, довольно обширен. Многие стереометрические задачи сводятся к поиску прямых углов в исследуемом объекте, после чего вопрос о существовании и нахождении неизвестных компонент переходит в область несложных вычислений.

О единственности подхода говорить не приходится, поскольку любые формулы, правила, свойства могут быть получены, исходя из различных базовых данных и условий.

Задача №1

Доказать, что каждая точка прямой, перпендикулярной плоскости треугольника и проходящей через центр вписанной окружности, равноудалена от его сторон.

Условие со всеми дополнительными построениями изображено на рисунке.

В силу касания окружностью сторон, каждый из радиусов OA, OB, OC образует угол в 90º. Отрезки SA, SB, SC составляют со сторонами прямые углы, а их длины являются искомыми расстояниями

ΔAOS = ΔBOS = ΔCOS по двум катетам (SO – общий, OA = OB = OC = r), следовательно, SA = SB = SC.

Задача №2

Основанием пирамиды MABCD служит прямоугольник со сторонами 6 и 8. Высота MB равна 2. МВ перпендикулярна плоскости прямоугольника АВСD.

Найти расстояние от точки M до диагонали CA и длину ребра MD.

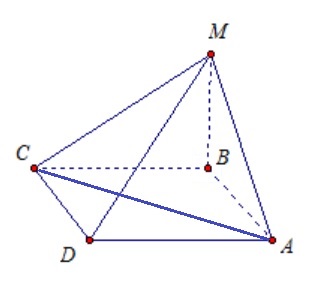
Для ответа на первый вопрос требуется знать определение расстояния. Это длина перпендикуляра, проведённого из данной точки на прямую.

Пусть MH – искомое расстояние. Тогда MH ⊥ AC.

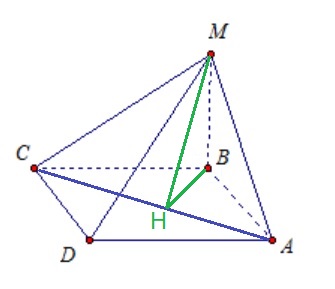
По второму утверждению BH ⊥ AC.

Поскольку ΔABC – прямоугольный, то BH, как высоту, можно вычислить по формуле:

Вычислить AC несложно:

Учитывая, что диагонали прямоугольника имеют одинаковые длины, находят MD:

Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна её проекции, то она перпендикулярна и самой наклонной (рис. 1).

Обратная теореме о трех перпендикулярах

Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна самой наклонной, то она перпендикулярна и её проекции.

Примеры решения задач

Задание. Через центр $O$ вписанной в треугольник $ABC$ окружности проведена прямая $SO$, перпендикулярная плоскости треугольника. Доказать, что каждая точка этой прямой равноудалена от сторон треугольника.

Доказательство. 1) Так как радиус $OA = r$ перпендикулярен стороне треугольника (рис. 2), то, согласно теореме о трех перпендикулярах, отрезок $SA$ перпендикулярен этой стороне.

2) Рассмотрим прямоугольный треугольник $SAO$. По теореме Пифагора

3) Аналогично, можно показать, что

То есть $SA = SB = SC$ .

Что и требовалось доказать

Мы помогли уже 4 372 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Задание. Высота прямоугольного треугольника $ABC$, опущенная на гипотенузу, равна 9,6. Из вершины $C$ прямого угла восставлен к плоскости треугольника $ABC$ перпендикуляр $CM$, причем $CM=28$. Найти расстояние от точки $M$ до гипотенузы $AB$.

Решение. Пусть $CH$ - высота заданного прямоугольного треугольника $ABC$ (рис. 3).

Тогда $MH$ - наклонная к плоскости треугольника $ABC$, а $CH$ - проекция этой наклонной на плоскость треугольника.

Так как $C H \perp A B$, то по теореме о трех перпендикулярах и $M H \perp A B$. Значит, длина отрезка $MH$ равна искомому расстоянию от точки $M$ до гипотенузы $AB$.

Рассмотрим чертеж. На нем изображены плоскость α и лежащая в ней прямая m. Наклонная a пересекает плоскость α в точке М. Прямая а₁ — проекция наклонной а на плоскость α.

Сформулируем теорему о трех перпендикулярах:

Прямая, лежащая в плоскости, перпендикулярна наклонной тогда и только тогда, когда она перпендикулярна проекции этой наклонной на данную плоскость.

На рисунке показаны все три перпендикуляра.

Если прямая m, лежащая в плоскости, перпендикулярна проекции наклонной, то она перпендикулярна и самой наклонной.

Ты нашел то, что искал? Поделись с друзьями!

Вот как все это выглядит в пространстве:

На нашем чертеже прямая m проведена через основание наклонной. Этого требует формулировка теоремы о трех перпендикулярах в большинстве учебников. Но прямая m, лежащая в плоскости, вовсе не обязана проходить через основание наклонной. Главное — чтобы она была перпендикулярна проекции наклонной. Тогда она будет перпендикулярна и самой наклонной:

Теорема о трех перпендикулярах — полезный инструмент для решения задач.

Например, с ее помощью можно доказать, что диагональ куба АС₁ перпендикулярна прямой BD:

Или — что скрещивающиеся ребра тетраэдра взаимно перпендикулярны:

Или — что в правильной треугольной призме прямая А₁М (где М — середина ВС) перпендикулярна ребру ВС.

Читайте также: