Течение жидкости в трубах реферат

Обновлено: 04.07.2024

Как следует из уравнения Бернулли, для компенсации потерь энергии (потерь напора) энергия в начале потока должна быть больше, чем в конце.

Источники энергии потока жидкости. Начальную энергию со­здают в форме удельной потенциальной энергии положения (гео­метрического напора) либо удельной потенциальной энергии дав­ления (пьезометрического напора).

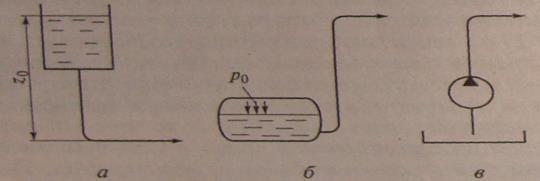
Потенциальную энергию положения запасают в напорных ба­ках (рис. 6.8, б), поднимая жидкость в поле сил тяжести на неко­торую высоту , которая и является начальным геометрическим напором.

Если на поверхности жидкости в замкнутом аппарате создать давление газа (рис. 6.8, б), то удельная потенциальная энергия давления также обеспечит движение жидкости в трубо­проводе. Такие аппараты называют монтежю.

Наиболее часто энергию в начале трубопровода создают насо­сом (рис. 6.8, в). Насос — это гидравлическая машина, предназна­ченная для передачи энергии потоку жидкости. Основная доля этой энергии — потенциальная энергия давления и частично — кине­тическая.

Потери напора по длине потока. Когда передвигают книгу по столу, то затрачивают энергию на преодоление силы трения о стол. При движении жидкости энергия будет затрачиваться на пре­одоление сил трения в жидкости. Экспериментально доказано, что при движении жидкости на стенке трубы образуется тончай­ший неподвижный слой этой жидкости. Поэтому даже на стенке трубы сохраняется жидкостное трение.

Потери напора на трение по длине трубы определяют по формуле:

где — коэффициент трения; l — длина трубы; d — ее диаметр: v 2 /(2g) — скоростной напор.

Очевидно, что чем больше длина трубы /, тем значительнее затраты энергии (напора) на преодоление трения. И наоборот, с увеличением диаметра трубы d затраты энергии уменьшаются, так как поверхность трения становится относительно меньше.

Значения коэффициента трения , приводимые в справочни­ках, зависят от режима течения жидкости, определяемого числом Рейнольдса, а в случае развитого турбулентного течения — и от степени шероховатости трубы.

Влияние шероховатости на величину потерь напора обусловле­но образованием вихрей на выступах неровностей трубы, что тре­бует затрат некоторой доли энергии потока. Различают абсолют­ную и относительную шероховатость.

Абсолютная шероховатость (е) — это высота выступов неровно­стей на стенках трубы. Она зависит от материала и способа изго­товления трубы. Значения абсолютной шероховатости приводятся в справочниках.

Относительная шероховатость — это отношение абсолютной шероховатости к диаметру трубы (e/d). При определении коэффи­циента трения обычно используют обратную величину — харак­теристику шероховатости (d/e).

При увеличении шероховатости возрастает число вихрей и по­вышаются потери напора. Например, потери напора в чугунной трубе больше, чем в стеклянной, при прочих равных условиях.

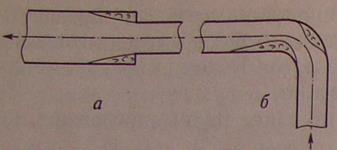
Потери напора на местных сопротивлениях. В трубопроводе ско­рость жидкости может изменяться по величине и направлению из-за наличия поворотов канала, сужений, установки различных регулирующих устройств и т.д. На таких участках, называемых мест­ными гидравлическими сопротивлениями, вследствие инерции жид­кость отрывается от стенок и образуются вихревые зоны. На фор­мирование вихрей затрачивается часть энергии потока. Примера­ми местных сопротивлений могут служить внезапное расширение потока и плавный поворот (отвод) трубы, показанные на рис. 6.9. В первом случае изменяется значение скорости, во втором — ее направление.

Потери напора на отдельном местном сопротивлении оп­ределяют по формуле

где — коэффициент местного сопротивления. Величина зависит от вида местного гидравлического сопротивления (ее значения опубликованы в справочной литературе).

Полные потери напора в трубопроводе. Производственные тру­бопроводы разнообразны как по расположению в пространстве, таки по оснащению их устройствами управления и вспомогатель­ным оборудованием.

Устройства управления служат для регулирования расхода жид­кости или полного перекрытия потока (кран, вентиль, задвиж­ка), ограничения давления в трубопроводе (предохранительный клапан), пропускания жидкости лишь в одном направлении (об­ратный клапан) и других целей.

К вспомогательным устройствам, устанавливаемым на трубопро­водах, относятся очистители жидкости (фильтры), гидроаккуму­ляторы (устройства для погашения гидравлического удара) и др.

Все элементы трубопроводов на гидравлических схемах имеют условные стандартные изображения. Саму трубу изображают сплош­ной линией.

На рис. 6.10 представлен пример схемы простого трубопровода. Его начало помечено цифрой 1, а конец — цифрой 2. Высота подъе­ма жидкости обозначена . Движение жидкости по трубопроводу сопровождается потерями напора одновременно по длине и на местных сопротивлениях. Их суммирование позволяет определить полные потери напора в трубопроводе. Для приведенной схемы

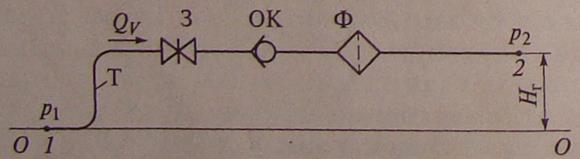
где , — потери напора по длине (на трение); — потери на одном отводе — плавном повороте (всего их два); — на преодоление сопротивления трубопроводной арматуры — задвиж­ки, обратного клапана и фильтра; — потери напора на выходе из трубы в резервуар. Заметим, что место выхода из трубы являет­ся частным случаем внезапного расширения, когда скорость жид­кости падает до нуля (в резервуаре).

Потребный напор. Пьезометрический напор в начале трубопро­вода , необходимый для пропускания по нему жид­кости с заданным расходом, называют потребным напором . Исходя из его значения подбирают марку насоса.

Обеспечение потребного напора (удельной энергии) в трубо­проводе сопряжено с подъемом жидкости на высоту , создани­ем необходимого пьезометрического напора в конце трубопрово­да преодолением общих потерь напора в трубо­проводе. Эти затраты удельной энергии можно представить в сле­дующем виде;

Трубопровод, схема которого приведена на рис. 6.10, называют простым, так как он не имеет ответвлений. Трубопроводы с ответ­влениями называют сложными.

В производственной практике применяют два основных вида сложных трубопроводов: с параллельным соединением труб и слож­ный тупиковый трубопровод.

Пример схемы параллельного соединения труб представлен на рис. 6.11. Здесь общий магистральный поток жидкости с расходом разделяется в точке М на параллельные потоки с расходами в ветвях, равными и . В точ­ке N потоки сливаются. Очевид­но, что расход в магистрали ра­вен сумме расходов в ветвях:

Это равенство справедливо, даже если ветви имеют неодина­ковую длину и диаметр, а также разные местные гидравлические сопротивления. При этом значения расходов и устанавли­ваются автоматически.

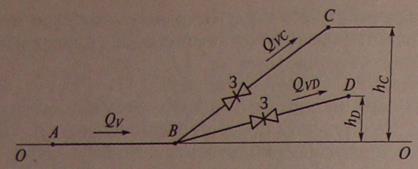
В сложном тупиковом трубопроводе (рис. 6.12) магистральный поток (участок АВ) разделяется на два потока (ветви ВС и BD). Очевидно, что сумма расходов в ветвях трубопровода равна рас­ходу в магистрали;

При решении практических задач обычно известны расходы в ветвях, напоры в конечных точках ( и H_D) и пространствен­ное размещение трубопровода, включая высоты конечных точек ( и ). Кроме того, известны геометрические параметры (дли­на и диаметр) труб, коэффициенты местных сопротивлений и свойства жидкости (плотность и вязкость). Общая задача, как пра­вило, сводится к определению потребного напора в точке А. Его значение, а также расход нужно знать для подбора на­соса.

При определении потребного напора весь сложный тру­бопровод разбивают на простые участки (АВ, ВС и BD) и нахо­дят необходимые параметры в отдельных точках схемы, начиная рассмотрение с конечных точек (С и D) и двигаясь навстречу потоку.

На приведенной схеме (см. рис. 6.12) напор в точке В одинаков для простых участков ВС и BD. При разных расходах и иных пара­метрах ветвей расчетные значения потребного напора (см. формулу (6.7)) для ветвей неодинаковы. Для проведения дальней­ших расчетов выбирают наибольшее из полученных значений .

При определении потребного напора в начале магистрали из схемы условно отбрасывают ветви ВС и BD. Далее расчет прово­дят, как для простого трубопровода АВ при известном напоре в конце его, равном .

Для достижения требуемых расходов и 1 ветвях или получения необходимого соотношения этих расходов используют задвижки 3, встроенные в ветви.

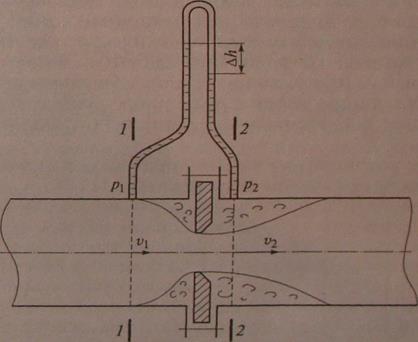
Устройства для измерения расхода. На производственных ус­тановках расход жидкости измеряют с помощью сужающих уст­ройств — дроссельных расходомеров. Наиболее простое по конст­рукции и широко распространенное устройство — диафрагма. Схема измерения расхода с помощью диафрагмы приведена на рис. 6.13.

Диафрагма представляет собой диск с отверстием определен­ной формы. Ее зажимают между усреднительными камерами, ко­торые необходимы для повышения точности измерения. К этим камерам подсоединяют дифференциальный манометр для изме­рения разности давлений до и после диафрагмы.

В сечении 1-1, до сужения потока, его скорость равна а давление в этом сечении — . При сужении потока в сечении 2-2 его скорость возрастает до величины . Другими словами, увеличивается скоростной напор, или удельная кинетическая энергия. Согласно уравнению Бернулли давление в сечении 2-2 становится меньше, чем в сечении 1-1. Появляется разность дав­лений и соответствующая ей разность уровней жид­кости , измеряемая манометром.

Зависимость разности давлений от расхода жидкости представ­ляют графически в форме градуировочной кривой, прилагаемой к каждой конкретной диафрагме. С помощью такой кривой по показаниям прибора можно определить расход жидкости.

Гидравлический удар. Явление гидравлического удара возника­ет в трубопроводах при резкой остановке потока жидкости. До сих пор мы пренебрегали ее сжимаемостью, считая, что при измене­нии давления объем жидкости не меняется. Но при гидравличе­ском ударе пренебрегать этим свойством жидкости нельзя.

Как возникает гидравлический удар? Рассмотрим простейшую трубопроводную схему (рис. 6.14). В горизонтальной трубе 2 жид­кость движется под действием постоянного геометрического на­пора го, создаваемого в водонапорной башне 1. При этом давле­ние на входе в трубу также постоянно и равно .На трубо­проводе установлен кран К, с помощью которого можно пере­крыть поток.

Давление, возникающее в трубе при полной остановке пото­ка, определяют по формуле Жуковского

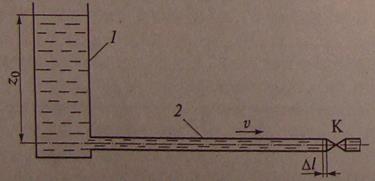
где v — начальная скорость потока; с — скорость звука в данной жидкости.

В качестве примера определим давление, возникающее в тру­бе в результате гидравлического удара, если жидкость (вода) имеет плотность р = 1000 кг/м 3 и начальную скорость движения v = 2 м/с. Скорость звука в воде примем равной с = 1500 м/с. Тогда давле­ние составит = 1000 • 2 • 1500 = 3 000 000 Па (3 МПа). Если предположить, что труба рассчитана на работу при давлении 0,6 МПа, то, естественно, при гидравлическом ударе она будет разрушена.

Как можно предотвратить возникновение гидравлического уда­ра? Одним из способов его предупреждения является установка вместо крана, резко перекрывающего поток, вентиля или задвижки. Конструктивно они выполнены так, что останавливают поток плав­но, уменьшая скорость жидкости постепенно. В этом случае может возникнуть лишь так называемый непрямой гидравлический удар с незначительным повышением давления.

Если по требованиям технологии производства или техники безопасности резкая остановка потока жидкости необходима, то на трубопроводе можно установить специальное устройство — гидроаккумулятор (воздушный колпак). При внезапном повыше­нии давления газ в полости гидроаккумулятора сжимается, и жид­кость поступает в эту полость, что предотвращает ее сжатие в трубе.

Вязкость. Коэффициент вязкости. Слоистое движение жидкости, возникающее при сильном влиянии трения. Воздействие статического давления на твердые тела, находящиеся в поле течения. Вязкий поток. Число Рейнольдса.

Вязкость. Коэффициент вязкости

В реальных жидкостях почти никогда нельзя пренебречь внутренним трением, вязкостью; большинство интересных вещей в поведении жидкости так или иначе связано с этим свойством. Циркуляция сухой воды (т.е. ее вязкость не учитывается) никогда не изменяется: если ее не было в начале, то она никогда не появится. В результате проведения экспериментов выясняется, что скорость жидкости на поверхности твердого тела не равна нулю. Можно заметить, что лопасти вентилятора собирают на себе тонкий слой пыли. Пыль не сдувается т.к. скорость воздуха относительно них, измеренная непосредственно на поверхности равна нулю. Теория должна учитывать, что во всех обычных жидкостях молекулы, находящиеся рядом с поверхностью имеют нулевую скорость (относительно самой поверхности).

Можно предположить, что если приложить к жидкости напряжение сдвига, то, сколь мало оно бы ни было, жидкость всё равно течет. В статическом случае никаких напряжений сдвига нет. Однако, когда равновесия еще нет, в момент, когда вы давите на жидкость, силы сдвига вполне могут быть. Вязкость как раз и описывает эти силы, возникающие в движущейся жидкости. Чтобы измерить силы сдвига в процессе движения жидкости, предположим, что имеются две плоские твердые пластины, между которыми находится вода. Причем одна из пластин неподвижна, тогда как другая движется параллельно ей с малой скоростью V₀ . Если измерять силу, требуемую для поддержания движения верхней пластины, выяснится, что она пропорциональна площади пластины и отношению V₀ /d, где d – расстояние между пластинами. Таким образом, напряжение сдвига F/A пропорционально V₀ /d:

Коэффициент пропорциональности h называется коэффициентом вязкости.

Внутреннее трение в жидкости можно показать и с помощью другого опыта: налить в стеклянный сосуд глицерин, ярко окрасив его нижний слой, получаем горизонтальную поверхность; поместим в сосуд пластинку (рис. 1).

Рис. 1.

Во время движения пластинки все горизонтальные поверхности с обеих ее сторон искривляются. При этом частички жидкости испытывают вращение, справа – по часовой стрелке, слева – против. Такую область называют пограничным слоем. Самая внутренняя часть пограничного слоя прилипает к пластинке и движется с такой же скоростью u, как и сама пластинка. Следующие части слоя тоже приводятся в движение, но скорость их тем меньше. Чем дальше они от пластинки. В пограничном слое устанавливается градиент скорости ¶u/¶ x. Если движение сопровождается трением, то сила F требуется не только для достижения конечной скорости, но и для поддержания этой постоянной скорости. Трение в жидкости можно сравнить со сдвигом или срезом в твердых телах, однако существует и коренное различие: в твердых телах напряжение сдвига растет с увеличением деформации; внутреннее трение, напротив, пропорционально скорости деформации.

Часто удобнее бывает пользоваться удельной вязкостью, которая равна h , деленной на плотность r . При этом величины удельных вязкостей воды и воздуха сравнимы:

Вода при температуре 20 0 С h/r =10 -6 м/сек,

Воздух при температуре 20 0 С h/r =15· 10 -6 м/сек.

Обычно вязкость очень сильно зависит от температуры.

Слоистое движение жидкости, возникающее при сильном влиянии трения

Наблюдаемое нами движение называется “слоистым” или “ламинарным”. Толщина слоя жидкости при этом меньше, чем толщина D, создаваемого трением пограничного слоя. Примером ламинарного течения может служить - течение жидкости в узкой трубке длиной l. Поддержание этого течения требует силы

Здесь u_m означает среднюю величину скорости течения, численно равную

u_m сила тока жидкости i/поперечное сечение трубки f

i=объем жидкости, протекающий через поперечное сечение f трубки/время течения t

Действительная скорость у поверхности трубки равна нулю, а в середине - наибольшая.

Течение жидкости в плоской, образованной двумя стеклянными пластинами кювете. Здесь возможно проследить пути отдельных частичек жидкости, которые образуют “нити тока”.

Введем в ламинарный поток препятствие в виде кружка, нити тока выглядят как на рисунке 2.

Рис.2.

Когда скорость очень мала или вязкость очень велика, можно отбросить инерционные члены и описать поток уравнением

где W - векторное поле,

Это уравнение впервые было решено Стоксом. Он так же решил задачу для сферы. Когда маленькая сфера движется при малых числах Рейнольдса (понятие числа Рейнольдса введено на странице 5), то к ней приложена сила, равная 6ph аV, где а – радиус сферы, V – его скорость. В области малых чисел Рейнольдса линии вокруг цилиндра выглядят так же, как на рисунке 2.

Качественной характеристикой, описывающей поток реальной жидкости, является сила, увлекающая цилиндр. На рисунке 3 графически изображена зависимость коэффициента увлечения С_d , отношения силы к 1/2rV 2 Dl (D – диаметр, l – длина цилиндра, r - плотность жидкости).

Воздействие статического давления на твердые тела, находящиеся в поле течения

Рисунок рис.4 показывает обтекаемый плоский диск в трёх положениях. Первое оказывается неустойчивым: диск устанавливается поперек течения. Мы видим пример этому на каждом падающем листе бумаги. Объяснение: при любом ничтожном наклонении возникает несимметричность в распределении статического давления, вследствие чего развивается вращательный момент. Это очевидно, когда диск находится под большим наклоном к течению (рис.4,б): области сгущенных линий тока тянут, а области расходящихся линий тока давят против диска, т.е. в ту же сторону. В результате, диск поворачивается по часовой стрелке (рис.4,б).

Вязкий поток

В общем случае сжимаемой жидкости в напряжениях есть и другой член, который зависит от производных скорости. Общее выражение имеет вид

Где d_ij обозначает символ Кронекера, который равен единице при i=j и нулю при i?j). Ко всем диагональным элементам S тензора напряжений прибавляется дополнительный член . Если жидкость несжимаема, торавно нулю и дополнительного члена не появляется, так как он действительно имеет отношение к внутренним силам при сжатии. Коэффициент h - коэффициент вязкости.

Число Рейнольдса

Если мы решили задачу для потока с одной скоростью V₁ и некоторого цилиндра диаметром D₁ а затем интересуемся обтеканием другого цилиндра диаметра D₂ другой жидкостью, то поток будет одним и тем же при такой скорости V₂ , которая отвечает тому же самому числу Рейнольдса, которое выражается зависимостью

VD

Это соответствует действительности только в том условии, что сжимаемостью жидкости можно пренебречь. В противном случае модели будут соответствовать, если будут одинаковы одновременно число Рейнольдса и число Маха (число Маха - отношение V к скорости звука). Таким образом, для скоростей, близких к скорости звука и больших, поток в обоих случаях будет одинаков, если и число Маха и число Рейнольдса равны.

Если увеличивать скорость потока так, что число Рейнольдса станет несколько больше единицы, то увидим, что поток изменился. За сферой возникают вихри (см рис. 5). Обычно считают, что циркуляция нарастает постепенно. Когда ? =от 10 до 30 поток меняет свой характер.

Когда число Рейнольдса проходит значение в районе 40, характер движения претерпевает неожиданное и резкое изменение. Один из вихрей за цилиндром становится настолько длинным, что отрывается и плывет вниз по течению вместе с жидкостью. При этом жидкость за цилиндром снова закручивается и возникает новый вихрь. Вихри отслаиваются то с одной, то с другой стороны и в какой-то момент вытягиваются вихревым следом за цилиндром. Такой поток вихрей называется цепочкой Кармана. Она всегда появляется для чисел Рейнольдса ?>40.

Можно представить физическую причину этих вихрей. Известно, что на поверхности цилиндра скорость жидкости должна быть равной нулю, но при удалении от поверхности скорость быстро возрастает. Это местное изменение скорости жидкости и создаёт вихри. Если скорость достаточно мала, у вихрей есть время “расплыться” на большую область. Когда ?достигает нескольких тысяч, вихри начинают заполнять тонкую ленту. В таком слое поток хаотичен и нерегулярен. Эта область называется пограничным слоем . Этот поток пробивает себе дорогу дальше и дальше. В этой области, турбулентности, скорости очень нерегулярны и беспорядочны. С увеличением числа Рейнольдса до 10 5 , мы получаем турбулентный след.

Всплывающий воздушный пузырек и закон Архимеда.

Когда пузырек всплывает, некоторая масса воды устремляется вниз, заполняя освобожденное место. Пузырек взаимодействует с движущейся, а не с неподвижной водой. Внешне это выглядит так, что c массой всплывающего пузырька движется “присоединенная масса” воды, которая равна ?m=Vr/2,т.е. половине массы вытесненной воды. Это происходит из-за сложного движения жидкости вокруг самого пузырька.

Ламинарные и турбулентные течения в природе и технике

Если подсчитать число Рейнольдса для атмосферных и океанских течений, то окажется, что они очень велики. Это указывает на то, что такие течения не могут быть ламинарными. Действительно, все мы видели, что даже легкий ветерок заставляет трепетать флаги, т. е. воздушные потоки имеют вихревую структуру. В природе вихри появляются в той части потока, где скорость быстро меняется в направлении, перпендикулярном потоку. Каждому приходилось видеть вихри в быстрой реке на переходе от быстрины к замедленному течению у берега. Целая цепочка вихрей может тянуться за движущимся автомобилем, что особенно удобно наблюдать в снегопад.

Вихревой характер сильного ветра был замечен в 1821 г. У. Рэдфилдом, содержателем небольшого магазина в штате Коннектикут (США), который обратил внимание на поваленные после шторма деревья. В одном месте деревья лежали макушками к северо-западу, тогда как на некотором расстоянии макушки указывали на прямо противоположное направление. Отсюда Рэдфилд сделал вывод, что шторм представляет собой вращательную систему ветров. Беседуя с моряками и анализируя судовые журналы, он установил направления вращения крупных вихрей и нашел траектории их центров. В 1831 году вышел труд У. Рэдфилда, излагающий результаты его исследований.

Оказалось, что вихревые системы в атмосфере Земли бывают двух видов – циклоны и антициклоны. В Северном полушарии Земли все циклоны вращаются против часовой стрелки, а антициклоны - по часовой, в Южном – наоборот. Направление вихрей определяется силой Кориолиса. В тропиках циклоны забирают энергию от нагретой поверхности океана и приобретают огромную мощь. За один день большой ураган расходует энергию, равную энергии взрыва 13 000 мегатонных ядерных бомб. Диаметр тропического циклона, его еще называют ураганом или тайфуном, составляет несколько сот километров, высота – до 12-15 км, скорость ветра достигает 400 – 600 км/час. Самые большие скорости ветра в урагане наблюдаются вокруг так называемого “глаза бури” - зоны покоя в центре урагана.

Внетропический циклон (называемый обычно просто циклоном) – это самый крупный атмосферный вихрь, достигающий в поперечнике нескольких тысяч километров в поперечнике. Высота его колеблется между 2 - 4 и 15 – 20 км. Скорость ветра в нем в большинстве случаев не превышает 40 – 70 км/час. Внетропические циклоны “глазом” не обладают.

Еще четче зона покоя (полость) выражена у мелкомасштабных вихрей – смерчей (торнадо, тромбов). Размеры их очень малы: ширина – от нескольких метров до 2 – 3 км, в среднем 200 – 400 м, высота от нескольких десятков до 1500 – 2000 м. Скорость ветра в смерче иногда превышает звуковую (1200 км/час!).

Если атмосферные вихри известны давно, аналогичная система океанских течений была обнаружена советскими океанологами в конце 20-го века. Это было выдающимся открытием.

В атмосфере больших планет также наблюдаются вихревые образования. Особенно удивительно так называемое Красное пятно на Юпитере, вихрь, устойчиво существующий в течение всех лет наблюдений в телескопы. На Солнце к вязкости, инерционным силам добавляются еще силы взаимодействия с магнитным полем. Это усложняет структуру солнечных протуберанцев. В межзвездных туманностях также можно наблюдать вихревые образования. Возможно, что галактики образовались как турбулентные вихри при расширении вещества Вселенной.

Ламинарное течение наблюдается при течении крови по капиллярам и кровеносным сосудам. Было обнаружено, что дельфины могут эффективно подавлять возникновение турбулентности, благодаря чему могут быстро и бесшумно перемещаться в воде. Созданные под влиянием этих исследований специальные покрытия позволили сделать бесшумные подводные лодки. Подводная лодка “Варшавянка”, она же “Kilo” или “Черная дыра” обладает шумностью на уровне естественных шумов океана.

Было обнаружено, что малые добавки некоторых полимеров переводят турбулентное течение в ламинарное. Это приводит к резкому снижению сопротивления. Сейчас эти добавки используются пожарными, чтобы увеличить скорость вытекания струи из брандспойта.

Вклад русских ученых в изучение турбулентности

В заключение следует отметить вклад русских ученых в изучение турбулентности. До 1941 года математической теории турбулентности не существовало, но было несколько великих ученых, которые пытались дать феноменологическое объяснение турбулентности. Андрей Николаевич Колмогоров думал о турбулентности примерно полгода. Потом наступила война, и он вынужден был переключиться на другие проблемы (его привлекли к задачам корректировки бомбометания и артиллерийского огня). Колмогоровым были опубликованы три маленькие статеечки в “Докладах Академии наук” общим объемом примерно в 15 страниц. И из этого выросла математическая теория турбулентности. В вышедшей в 1998 году монографии французского ученого Уриэла Фриша “Турбулентность. Наследие Колмогорова” есть такие слова: “Глубже всех проник в суть турбулентности именно Колмогоров – математик, обладавший страстным интересом к живой действительности”. Библиография книги Фриша содержит более 600 работ последователей Колмогорова. В настоящее время ученик Колмогорова А.М. Яглом пишет серию книг по колмогоровской теории турбулентности из семи томов. Выдающийся бельгийский ученый И. Пригожин поставил вопрос о присуждении Колмогорову Нобелевской премии, но слишком поздно, когда Андрею Николаевичу осталось жить всего полгода.

В 2003 году другой русский ученый академик Владимир Захаров получил медаль имени Дирака за “выдающийся вклад в теорию турбулентности”. Медаль Дирака – вторая по значимости после Нобелевской премии награда в науке. В. Захаров 15 лет руководил Институтом теоретической физики им. Ландау в Черноголовке.

Список литературы

Р.В. Поль - “Механика, акустика и учение о теплоте”. Издательство “Наука” Главная редакция физико-математической литературы Москва 1971г.

Р. Фейнман, Р. Лейтон, М. Сэндс – “Фейнмановские лекции по физике” т. 7 “Физика сплошных сред”. Издательство “Мир”, Москва, 1966г.

М. Калашников – “Сломанный меч империи”. Крымский мост-9Д, Палея, Форум, Москва, 1999г.

В.А. Тихомирова, А.И. Черноуцан - “Физический факультатив”, Приложение к журналу “Квант”, Москва, 2001г.

Л. Алексеев - “Вихри, которые “делают погоду””. Журнал “Квант” №8 1977г.

В. Тихомиров - “Андрей Николаевич Колмогоров (к 100-летию со дня рождения)”. Журнал “Квант”, №3, 2003г.

Отличительные особенности турбулентного течения жидкости в гладких и шероховатых трубах, обоснование характерного для него перемешивания жидкости, пульсации скоростей и давлений в течении. Основы полуэмпирической теории, отражающей данный процесс.

Рубрика	Физика и энергетика
Вид	лекция
Язык	русский
Дата добавления	12.06.2017
Размер файла	233,3 K

Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.

Турбулентное течение

Для турбулентного течения характерно перемешивание жидкости, пульсации скоростей и давлений в процессе течения. Если с помощью особо чувствительного прибора-самописца измерить и записать пульсацию, например, скорости по времени, то получим картину, подобную показанной на рис. 57. Величина скорости беспорядочно колеблется около некоторого осредненного по времени значения _оср, которое в данном случае остается постоянным.

Траектории частиц, проходящих через данную неподвижную точку пространства, в разные моменты времени представляют собой кривые линии различной конфигурации несмотря на прямолинейность трубы. Характер линий тока в трубе в данный момент времени также отличается большим разнообразием (рис. 58). Таким образом, строго говоря, турбулентное течение является неустановившимся течением, так как величины скоростей и давлений, а также траектории частиц меняются по времени. Однако в расчетах его можно рассматривать как установившееся при условии, что осредненные по времени значения скоростей и давлений, а также величина полного расхода потока, не меняются с течением времени. Такое течение жидкости встречается на практике достаточно часто.

Ввиду того, что при турбулентном течении отсутствует слоистость потока и происходит перемешивание жидкости, закон трения Ньютона в этом случае неприменим. Вследствие перемешивания жидкости и непрерывного переноса количеств движения в поперечном направлении касательное напряжение на стенке трубы в турбулентном потоке значительно больше, чем в ламинарном при тех же значениях числа Rе и динамического давления, подсчитанных по средней скорости потока.

Распределение скоростей (осредненных по времени) в поперечном сечении турбулентного потока существенно отличается от того, которое характерно для ламинарного течения.

Если сравнить кривые распределения скоростей в одной и той же трубе и при одном и том же расходе (одинаковой средней скорости), но при ламинарном и турбулентном режимах, то будет заметно существенное различие в указанных кривых. Распределение скоростей при турбулентном режиме более равномерно, а нарастание скорости у стенки - более крутое, чем при ламинарном режиме, для которого, как уже известно, характерен параболический закон скоростей.

В связи с этим коэффициент , учитывающий неравномерность распределения скоростей в уравнении Бернулли, при турбулентном режиме значительно меньше, нежели при ламинарном. В отличие от ламинарного режима, где он не зависит от числа Rе, здесь коэффициент является функцией числа Rе, уменьшаясь с увеличением последнего от 1,13 при Rе=Rе_кр, до 1,025 при Rе=3 * 10 6 . Как видно из графика, приведенного на рис. 60, кривая по Rе асимптотически приближается к единице. В большинстве случаев при турбулентном течении можно принимать =1.

Потери энергии при турбулентном течении жидкости в трубах постоянного сечения (т.е. потери напора на трение) также получаются иными, нежели при ламинарном. В турбулентном потоке потери напора на трение значительно больше, чем в ламинарном при тех же размерах, расходе и вязкости.

Это увеличение потерь вызывается вихреобразованиями, перемешиванием и искривлением траекторий. Если при ламинарном режиме течения потеря напора на трение возрастает пропорционально скорости (а также расходу) в первой степени, то при переходе к турбулентному режиму заметен некоторый скачок сопротивления и затем более крутое нарастание величины h_тр по кривой, близкой к параболе второй степени.

Ввиду сложности турбулентного режима течения и трудностей его аналитического исследования, до сих пор мы еще не имеем достаточно строгой и точной теории этого течения. Существуют так называемые полуэмпирические, приближенные теории турбулентности Прандтля, Кармана и др.

В большинстве случаев для практических расчетов, связанных с турбулентным течением жидкостей в трубах, пользуются чисто экспериментальными данными, систематизированными на основе гидродинамической теории подобия.

Основной расчетной формулой для турбулентного течения в круглых трубах является уже приводившаяся выше универсальная формула, которая непосредственно вытекает из соображений подобия и имеет следующий вид:

Эта основная формула применима как при турбулентном, так и при ламинарном режимах; различие заключается в значениях коэффициента .

Так как при турбулентном течении потеря напора на трение приблизительно пропорциональна квадрату скорости (и квадрату расхода), то коэффициент потерь на трение в формуле в первом приближении для данной трубы можно считать величиной постоянной.

Однако из закона гидродинамического подобия следует, что коэффициент _т, так же как и _л, должен являться функцией основного критерия подобия, т.е. числа Рейнольдса, включающего в себя скорость, диаметр и вязкость, т.е.

Существует ряд эмпирических и полуэмпирических формул, выражающих эту функцию для турбулентного течения в гладких трубах; одной из наиболее удобных и употребительных является формула П.К. Конакова, имеющая следующий вид

и применима от Rе=Rе_кр до Re, равного нескольким миллионам.

При числах Рейнсльдса 2300 5 можно пользоваться также старой формулой Блазиуса

Отсюда видно, что с увеличением числа Re коэффициент _т уменьшается, однако это уменьшение гораздо менее значительно, чем при ламинарном режиме.

Это различие в законах изменения коэффициента связано с тем, что непосредственное влияние вязкости жидкости на сопротивление в турбулентном потоке гораздо меньше, чем в ламинарном. Если в последнем потери напора на трение прямо пропорциональны вязкости, то в турбулентном потоке эти потери пропорциональны вязкости в степени 1/4. Дело в том, что основную роль в турбулентном потоке играют перемешивание и перенос количеств движения.

Приведенные формулы для определения коэффициента потерь на трение справедливы для так называемых технически гладких труб, т.е. для таких, шероховатость которых столь мала, что на сопротивление практически не влияет. К числу технически гладких труб можно без большой погрешности отнести цельнотянутые трубы из цветных металлов (включая и алюминиевые сплавы), а также бесшовные стальные трубы тщательного изготовления. Таким образом, трубы, употребляемые на самолетах в качестве топливопроводов и для гидропередач (гидросистем), в обычных условиях можно считать гладкими и для их расчета пользоваться приведенными формулами. Водопроводные стальные и чугунные трубы уже нельзя считать гладкими, так как они обычно дают повышенное сопротивление.

Вопрос о сопротивлении шероховатых труб будет рассмотрен ниже (см. § 30).

Как следует из теории подобия, при турбулентном течении жидкости в трубах непосредственно на стенке трубы обычно имеется так называемый ламинарный слой. Это весьма тонкий слой жидкости, движение в котором является наиболее замедленным, слоистым и без перемешивания, т.е. ламинарным.

В пределах этого ламинарного сдоя скорость круто нарастает от нулевого значения на стенке до некоторой конечной величины на границе слоя. Толщина ламинарного слоя _л крайне невелика, причем оказывается, что число Re, подсчитанное по параметрам слоя есть величина постоянная, т.е.

Эта величина имеет универсальное постоянное значение подобно тому, как постоянно критическое число Re для течения в трубах. Поэтому, при увеличении скорости потока, а следовательно, и числа Re, растет также скорость, а толщина ламинарного слоя уменьшается. При больших числах Re ламинарный слой практически исчезает.

2. Основы полуэмпирической теории турбулентного течения в трубах

Из описания турбулентного течения следует, что истинную местную скорость в турбулентном потоке в данный момент времени следует рассматривать как сумму осредненной по времени скорости и некоторого положительного или отрицательного приращения, называемого пульсационной скоростью. Условимся обозначать величины, осредненные по времени, чертой вверху, а пульсационные скорости - штрихом.

Тогда для составляющей местной скорости вдоль оси трубы (ось х) можно записать

t - отрезок времени, за который осредняется скорость.

Так как осредненный поток вдоль осей у и z в прямой трубе постоянного сечения отсутствует, то соответствующие составляющие скорости равны нулю. Очевидно, что осредненное значение пульсационных скоростей, определенное таким же способом за достаточный промежуток времени, равно нулю. т.е.

Осредненное значение касательного напряжения за промежуток времени t:

Полученное выражение именуется формулой Л. Прандтля и является законом турбулентного трения, который используется в теории турбулентных течений так же, как закон трения Ньютона в теории ламинарных течений.

Очевидно, что в разных точках поперечного сечения трубы величина l имеет разные значения. На стенке трубы и в пределах ламинарного слоя, где поперечные перемещения частиц отсутствуют, величина l равна нулю.

По мере удаления от стенки (точнее - от границы ламинарного слоя) увеличивается возможность поперечных перемещений частиц, турбулентное перемешивание делается все более интенсивным и путь смешения l растет.

Л. Прандтль предложил считать, что l растет по линейному закону в зависимости от расстояния до стенки у, т.е.

где -коэффициент пропорциональности, имеющий, как показывают опыты, одинаковое значение для всех случаев турбулентного течения (порядка 0,4) и называемый поэтому универсальной постоянной турбулентного потока.

Далее Прандтль, рассматривая течение вдоль бесконечной плоскости, положил касательное напряжение в турбулентном потоке постоянным и равным напряжению на стенке _о.

При этих допущениях из формулы получаем после интегрирования -

(знак осреднения у скорости здесь и в дальнейшем опускается).

Таким образом, закон распределения скоростей в турбулентном потоке по теории Прандтля получается логарифмическим.

Путем несложных преобразований формулу можно привести к следующему безразмерному виду:

Закон распределения скоростей в последней форме называется универсальным законом, так как опытные точки, полученные в разных трубах и при различных числа Re, ложатся на единую кривую. Еще более показательным является график зависимости.

Теория Прандтля может быть уточнена путем учета вязкости ламинарного слоя.

Можно получить упрощенную форму закона распределения скоростей в турбулентном потоке с учетом ламинарного слоя и вязкости в виде

После несложных преобразований получим уточненный закон сопротивления в следующем виде:

Таким образом, постоянные коэффициенты выражаются через две универсальные константы, определение которых из опытов =0,401-0,407 и =6,82-6,93.

Итак, учет вязкости и ламинарного слоя в теории Прандтля позволяет получить уточненные законы распределения скоростей и сопротивления, обеспечивает удовлетворение граничному условию закона распределения скоростей вблизи стенки и дает возможность выразить все постоянные коэффициенты через две универсальные константы и .

турбулентный жидкость труба

3. Турбулентное течение в шероховатых трубах

Если для гладких труб коэффициент потерь на трение вполне определяется числом Re, то для шероховатых труб его значение зависит еще и от шероховатости внутренней поверхности трубы. При этом важен не абсолютный размер бугорков шероховатости k, а отношение этого размера к радиусу трубы, т.е. так называемая относительная шероховатость k/r_o. Одна и та же абсолютная шероховатость может совершенно не сказаться на сопротивлении трубы большого диаметра, но способна значительно увеличить сопротивление трубы малого диаметра. Кроме того, на сопротивление влияет характер шероховатости: расстояния между бугорками, неравномерность по высоте и пр. Простейшим случаем будет тот, когда все бугорки шероховатости имеют один и тот же размер k и одинаковую форму, т.е. при так называемой равномерно распределенной зернистой шероховатости.

Таким образом, в случае равномерно распределенной зернистой шероховатости коэффициент _т:

1) При ламинарном режиме шероховатость на сопротивление не влияет.

2) Критическое число Re от шероховатости практически не зависит.

3) В области турбулентного течения, но при небольших значениях Re и k/r₀, шероховатость на сопротивление не влияет. Однако при увеличении числа Re это влияние начинает сказываться.

4) При больших значениях числа Re и больших относительных шероховатостях коэффициент _т перестает зависеть от числа Re и делается постоянным для данной относительной шероховатости.

Можно отметить, следующие три области чисел Re и k/r_o, отличающиеся друг от друга характером изменения коэффициента _т.

Первая область-область малых Re и k/r_o, где коэффициент от шероховатости не зависит, а определяется лишь числом Re, как для гладких труб.

Вторая область, где коэффициент _т зависит одновременно от двух параметров: от числа Re и от относительной шероховатости,

Третья область - область больших Re и k/r_o, где коэффициент _т не зависит от числа Re, а определяется лишь относительной шероховатостью. Эту область называют областью автомодельности или режимом квадратичного сопротивления, так как независимость коэффициента _т от числа Re означает, что потеря напора пропорциональна точно квадрату скорости.

Необходимо учесть также наличие ламинарного слоя. Как указывалось, при увеличении числа Re толщина ламинарного слоя уменьшается. Поэтому, когда мы имеем турбулентный поток в шероховатой трубе, то при малых числах Re толщина ламинарного слоя больше величины бугорков шероховатости, последние находятся внутри ламинарного слоя, обтекаются плавно (безотрывно) и на сопротивление не влияют. По мере увеличения числа Re толщина уменьшается, бугорки шероховатости начинают выступать за пределы слоя и влиять на величину сопротивления. При больших числах Re толщина ламинарного слоя делается исчезающе малой, а бугорки шероховатости обтекаются турбулентным потоком со срывом и вихреобразовниями за каждым бугорком; этим и объясняется квадратичный закон сопротивления, имеющийся в данной области.

Для практических расчетов по определению сопротивления реальных шероховатых труб можно рекомендовать также следующую новую универсальную формулу А.Д. Альтшуля:

где d-диаметр трубы; k'-размер, пропорциональный абсолютной шероховатости.

Формула для вполне шероховатых труб, т.е. для режима квадратичного сопротивления (автомодельности)

4. Турбулентное течение в некруглых трубах

Выше мы рассматривали турбулентное течение в трубах круглого сечения. Однако иногда приходится иметь дело с турбулентным течением в некруглых трубах, применяемых, например, в охлаждающих устройствах.

Рассмотрим расчет потерь на трение при турбулентном течении в трубе с поперечным сечением произвольной формы.

Суммарную силу трения, действующую на внешнюю поверхность потока, можно выразить следующим образом:

где П-периметр сечения;

При заданной площади сечения и данном расходе жидкости (а следовательно, и при заданной средней скорости) сила трения пропорциональна периметру сечения. Поэтому для уменьшения силы трения, а также потерь энергии на трение следует периметр сечения уменьшать. Наименьшим периметром при заданной площади обладает круглое сечение, которое поэтому является наивыгоднейшим с точки зрения получения минимальных потерь энергии (напора) на трение в трубе.

Для количественной оценки влияния формы сечения на потерю. напора вводится в расчет так называемый гидравлический радиус R_r, равный отношению площади сечения трубы к его периметру:

Гидравлический радиус может быть подсчитан для любого сечения. Например, для круглого сечения имеем

для прямоугольного сечения со сторонами а и b:

Для зазора размером а из предыдущего получаем:

Подставив выражение геометрического диаметра d через гидравлический радиус в основную формулу для потери напора на трение, будем иметь:

Опыт подтверждает применимость формулы для труб с любой формулой поперечного сечения. Число Рейнольдса выражается через R_r, т.е.

Подобные документы

Расчет потерь напора при турбулентном режиме движения жидкости в круглых трубопроводах и давления нагнетания насоса, учитывая только сопротивление трения по длине. Определение вакуума в сечении, перемешивания жидкости, пульсации скоростей и давлений.

контрольная работа [269,2 K], добавлен 30.06.2011

Характеристика турбулентного режима течения, определение ее зависимости от числа Рейнольдса. Значения абсолютной и эквивалентной шероховатости труб из некоторых материалов. Режимы течения в гидравлически гладких трубах, описание специальной установки.

реферат [347,2 K], добавлен 18.05.2010

Рассмотрение и нахождение основных характеристик плоского стационарного ламинарного течения вязкой несжимаемой жидкости при параболическом распределении скоростей (течение Пуазейля и течение Куэтта). Общий случай течения между параллельными стенками.

курсовая работа [1,5 M], добавлен 28.12.2010

Выведение уравнения движения вязкой несжимаемой жидкости - уравнения Стокса. Рассмотрение основных режимов движения жидкости в горизонтальных трубах постоянного поперечного сечения - ламинарного и турбулентного. Определение понятия профиля скорости.

презентация [1,4 M], добавлен 14.10.2013

Сущность осредненного и пульсационного движения. Расчет сопротивления при турбулентном течении жидкости по каналам. Изучение понятия относительной и эквивалентной абсолютной шероховатости поверхности. Определение потери энергии в местных сопротивлениях.

Ламинарное течение — это слоистое течение без перемешива­ния частиц жидкости и без пульсаций скорости. При таком течении все линии тока вполне определяются формой русла, по которому течет жидкость. При ламинарном течении жидкости в прямой трубе постоянного сечения все линии тока направлены параллель­но оси трубы, т. е. прямолинейны; отсутствуют поперечные пере­мещения частиц жидкости, а потому не происходит перемешивания жидкости в процессе ее течения Пьезометр, присоединенный к трубе с установившимся ламинарным течением, показывает неизмен­ность давления (и скорости) по времени, отсутствие колебаний (пульсаций). Таким образом, ламинарное течение является вполне упорядоченным и при постоянном напоре строго установившимся течением (хотя в общем случае может быть и неустановившимся)

Однако ламинарное течение нельзя считать безвихревым, так как в нем хотя и нет ярко выраженных вихрей, но одновременно с поступательным движением имеет место упорядоченное враща­тельное движение отдельных частиц жидкости вокруг своих мгно­венных центров с вполне определенными угловыми скоростями.

Турбулентное течение — это течение, сопровождающееся интенсивным перемешиванием жидкости и пульсациями скоростей и давлений. При турбулентном течении линии тока лишь примерно определяются формой русла. Движение отдельных частиц оказы­вается неупорядоченным, траектории подчас имеют вид замысловатых кривых. Объясняется это тем, что при турбулентном течении наряду с основным продольным перемещением жидкости вдоль русла имеют место поперечные перемещения и вращательное дви­жение отдельных объемов жидкости.

Смена режима течения данной жидкости в трубе происходит при определенной скорости течения, которую называют критиче­ской. Как показывают опыты, значение этой скорости прямо пропорционально кинематическому коэффициенту вязкости и обратно пропорционально диаметру трубы, т. е.

Оказывается, что входящий сюда безразмерный коэффициент пропорциональности k имеет универсальное значение, т. е. одинаков для всех жидкостей и газов и любых диаметров труб. Это означает, что смена режима течения происходит при впол­не определенном соотношении между скоростью, диаметром и вяз­костью, равном

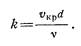
Это безразмерное число называется критическим числом Pейнольдса по имени английского ученого, который установил этот критерий, и обозначается

Как показывают опыты, критическое число Рейнольдса прибли­зительно равно 2300.

Однако можно говорить не только о критическом числе Re_кр, соответствующем смене режима, но и о фактическом числе Рей­нольдса для того или иного потока и выражать его через факти­ческую скорость, т. е.

Таким образом, мы получаем критерий, позволяющий судить о режиме течения жидкости в трубе. При значениях числа Rе Rе_кр течение обычно турбулентное.

Зная скорость течения жидкости, диаметр трубы и вязкость жидкости, можно расчетным путем определить режим течения жид­кости, что очень важно для последующих гидравлических расчетов.

Ламинарные течения на практике встречаются в тех случаях, когда по трубам движутся весьма вязкие жидкости, например, сма­зочные масла, глицериновые смеси и др.

Турбулентное течение обычно имеет место в водопроводах, а также в трубах, по которым движутся бензин, керосин, спирты и кислоты. Таким образом, на самолете приходится сталкиваться как с ламинарным, так и с турбулентным режимами течения жид­костей в трубах; в самолетных маслосистемах и гидропередачах режим течения чаще всего ламинарный, а в топливных системах — турбулентный.

Смена режимов течения при достижении числа Rе_кр объясняет­ся тем, что один режим течения теряет устойчивость, а другой ее приобретает. При Re Re_кp, наоборот, турбулентный режим устойчив, а лами­нарный — неустойчив.

В связи с этим критическое число Re_кp, соответствующее пере­ходу от ламинарного режима к турбулентному, может получиться несколько больше, чем Re_кp для обратного перехода. В особых ла­бораторных условиях при полном отсутствии факторов, способст­вующих турбулизации потока, удается получить ламинарный ре­жим при числах Re, значительно больших Re_кp. Однако в этих случаях ламинарное течение оказывается настолько неустойчивым, что достаточно, например, небольшого толчка, чтобы ламинарный поток быстро превратился в турбулентный. На практике, особенно в самолетных трубопроводах, мы обычно имеем условия, способ­ствующие турбулизации, — вибрация труб, местные гидравлические сопротивления, неравномерность (пульсации) расхода и пр., а по­тому указанное обстоятельство имеет в гидравлике скорее прин­ципиальное значение, чем практическое.

Точнее говоря, вполне развитое турбулентное течение в трубах устанавли­вается при Re> Re’_кp=4000, а при Re=2300—4000 имеет место переходная, кри­тическая область.

Вопрос об устойчивости ламинарного режима течения и о ме­ханизме турбулизации теоретически пока еще полностью не решен. Но исследования показывают, что в данном сечении цилиндрической трубы турбулизации способствуют такие факторы, как рас­стояние от стенки, величина скорости и ее поперечного градиента du/dy. Наибольшее расстояние от стенки и наибольшая скорость имеют место в центре потока, но там равен нулю градиент. У стенки, наоборот, градиент скорости наибольший, а скорость и расстояние у наименьшие или даже равны нулю. Поэтому на­чальная турбулизация ламинарного потока в прямой трубе посто­янного сечения начинается где-то в промежутке между осью трубы и стенкой, но все же ближе к стенке.

В трубах переменного сечения турбулизация потока происхо­дит не так, как в цилиндрической трубе. В расширяющихся тру­бах наблюдается замедление течения, усиливается тенденция к поперечному перемешиванию и значение Re_кp уменьшается. В су­жающихся трубах происходит ускорение течения и выравнивание скоростей по сечению, тенденция к перемешиванию уменьшается, а значение Re_кp увеличивается.

ГИДРОДИНАМИЧЕСКОЕ ПОДОБИЕ

Полученное в предыдущем параграфе число Рейнольдса имеет большое значение в гидравлике, а также в аэродинамике, так как является одним из основных критериев гидродинамического подо­бия. Гидродинамическое подобие — это подобие потоков несжимаемой жидкости, включающее в себя подобие геометрическое, кине­матическое и динамическое.

Геометрическое подобие, как известно из геометрии, означает пропорциональность сходственных размеров и равенство соответствующих углов. В гидравлике под геометрическим подоби­ем мы будем понимать подобие тех поверхностей, которые ограни­чивают потоки жидкостей, т. е. подобие русел (рис. 40).

Кинематическое подобие — это подобие линий тока и пропорциональность сходственных скоростей. Очевидно, что для кинематического подобия потоков требуется геометрическое подо­бие русел.

Динамическое подобие означает пропорциональность сил, действующих на сходственные элементы кинематически подоб­ных потоков и равенство углов, характеризующих направление этих сил.

В потоках жидкостей обычно действуют разные силы — давле­ния, вязкости (трения), тяжести и др. Соблюдение пропорциональ­ности всех этих разнородных сил означает так называемое полное гидродинамическое подобие.

Например, пропорциональность сил давления Р и сил трения Т, действующих на сходственные объемы в потоках / и //, можно написать в виде

Осуществление на практике полного гидродинамического подо­бия оказывается весьма затруднительным, поэтому обычно имеют дело с частичным (неполным) подобием, при котором наблюдается пропорциональность лишь главных, основных сил. Для напорных те­чений в закрытых руслах, т. е. для потоков в трубах, в гидравли­ческих машинах и т. п., такими главными силами, как показывают расчеты, являются силы давления, трения и их равнодействующие, т. е. силы инерции. Последние, как это можно показать для подоб­ных потоков, пропорциональны произведению динамического давления ru 2 /2 на характерную площадь S.

Для геометрически и кинематически подоб­ных потоков и сходственных частиц можно записать:

Для подобных потоков / и // будем иметь

Последнее отношение, одинаковое для подобных потоков, назы­вается числом Ньютона и обозначается Ne.

Заметим попутно, что этому же произведению ru 2 _срS в подоб­ных потоках пропорциональны силы, с которыми поток воздей­ствует (или способен воздействовать) на преграды: твердые стенки, лопасти гидромашин, обтекаемые потоком тела и т. п.

Так, например, если поток жидкости наталкивается на безграничную стенку (см. рис. 41), установленную нормально к нему, и в резуль­тате, растекаясь по стенке, меняет свое направление на 90°, то на основании теоремы механики о количестве движения секундный импульс силы равен

Это и есть сила воздействия на преграду. При другом угле уста­новки стенки или другой ее форме и размерах вместо единицы будет другой коэффициент пропорциональности.

Вначале рассмотрим наиболее простой случай — напорное дви­жение идеальной жидкости, т. е. такое движение, при котором отсутствуют силы вязкости, а действие силы тяжести проявляется через давление.

Для этого случая уравнение Бернулли для сечений 1—1 и 2—2 (см. рис. 40) имеет следующий вид:

Для двух геометрически подобных по­токов правая часть уравнения имеет одно и то же значение: следовательно, левая часть тоже одинакова, т. е. разности давлений пропорциональны динамическим явлениям:

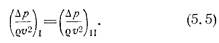
Таким образом, при напорном движении идеальной несжимае­мой жидкости для обеспечения гидродинамического подобия достаточно одного геометрического подобия. Безразмерная величина, представляющая собой отношение разности давлений к динамическому давлению (или разности пьезометрических высот к скорост­ной высоте), называется коэффициентом давления или числом Эйлера и обозначается Еu.

Посмотрим, какому условию должны удовлетворять те же гео­метрически и кинематически подобные потоки, для того чтобы было обеспечено их гидродинамическое подобие при наличии сил вяз­кости, а следовательно, и потерь энергии, т. е. при каком условии числа Ей будут одинаковыми для этих напорных потоков.

Уравнение Бернулли теперь будет иметь следующий вид:

Как видно из уравнения (5.6), числа Еu будут иметь одинако­вые значения для рассматриваемых потоков и потоки будут по­добны друг другу гидродинамически при условии равенства коэф­фициентов сопротивления z, (равенство коэффициентов a₁ и a₂ для сходственных сечений двух потоков следует из их кинематического подобия). Таким образом, коэффициенты z в подобных потоках должны быть одинаковыми, а это значит, что потери напора для сходственных участков (см. рис. 40) пропорциональны скоростным напорам, т. е.

Рассмотрим очень важный в гидравлике случай движения жид­кости — движение с трением в цилиндрической трубе, для кото­рого

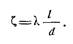
Для геометрически подобных потоков отношение l/d одинаково, следовательно, условием гидродинамического подобия в данном случае является одинаковое значение для этих потоков коэффи­циента l. Последний на основании формулы выражается через напряжение трения на стенке t_о и динамическое давление следующим образом:

Следовательно, для двух подобных потоков I и II можно запи­сать

т. е. напряжения трения пропорциональны динамическим давле­ниям.

Условие динамического подобия по­токов:

или, переходя к обратным величинам,

В этом заключается закон подобия Рейнольдса, который можно сформулировать следующим образом: для гидродинамиче­ского подобия геометрически подобных потоков с учетом сил вязкости требуется равенство чи­сел Рейнольдса, подсчитанных для любой пары сходственных сечений этих потоков.

Число Re есть величина, пропорциональная отношению динамиче­ского давления к напряжению трения или, что то же самое, от­ношению сил инерции к силам вязкости. Чем больше скорость и поперечные размеры потока и чем меньше вязкость жидкости, тем больше число Re. Для потока идеальной жидкости число Re бесконечно велико, так как вязкость n=0.

В случаях безнапорных течений под действием разности нивелирных высот вопрос о подобии осложняется, так как приходится вводить еще один критерий подобия — число Фруда, учиты­вающее влияние на движение жидкости силы тяжести. Однако для подавляющего большинства интересующих нас задач в области авиационной техники этот критерий не имеет значения, и мы его рассматривать не будем.

Итак, в подобных потоках, мы имеем равенство безразмерных коэффициентов и чисел a, z, l, Eu, Ne, Re и некоторых других, которые будут введены и рассмотрены ниже. Изменение числа Re означает, что меняется соотношение основных сил в потоке, в связи с чем указанные коэффициенты могут также меняться. Поэтому все эти коэффициенты в общем случае следует рассматривать как функции числа Re (хотя в некоторых интервалах числа Re они могут оставаться постоянными).

Читайте также:

  
• Реферат поэзия чистого искусства фета
  
• Установление фашистской диктатуры в германии реферат
  
• Влияние образа жизни на здоровье реферат по физкультуре
  
• Умышленное причинение легкого вреда здоровью реферат
  
• Гегель наука логики реферат