Реферат схемы повторных испытаний бернулли
Обновлено: 05.07.2024
- Для учеников 1-11 классов и дошкольников
- Бесплатные сертификаты учителям и участникам
Я выбралаэту тему потому что, на схемах Бернулли установление важные закономерностей теории вероятностей как математической науки, относящихся к сумме независимых случайных величин и представляющих закон больших чисел. Под законом больших чисел в теории вероятностей принято понимать ряд математических теорем, устанавливающих факт приближения средних характеристик большого числа испытаний к некоторым определенным постоянным. Важные теоремы, составляющие закон больших чисел, впервые были выведены для схемы испытаний Бернулли.
При практическом применении теории вероятностей часто приходится встречаться с задачами, в которых одно и то же испытание повторяется неоднократно. В результате каждого испытания может появиться или не появиться некоторое событие А, причем нас не интересует результат каждого отдельного испытания, а общее число появлений события А в результате серии опытов. Например, если производится группа выстрелов по одной и той же цели, нас, как правило, не интересует результат каждого выстрела, а общее число попаданий. В подобных задачах требуется уметь определять вероятность любого заданного числа появлений события в результате серии опытов. Такие задачи и будут рассмотрены. Они решаются весьма просто в случае, когда испытания являются независимыми.
Определение. Испытания называются независимыми, если вероятность того или иного исхода каждого из испытаний не зависит от того, какие исходы имели другие испытания.
Например, несколько бросаний монеты представляют собой независимые испытания.
Пусть произведено два испытания(n=2). В результате возможно наступление одного из следующих событий:
Соответствующие вероятности данных событий такие:
или — наступление события только в одном испытании.
— вероятность наступления события два раза.
— вероятность наступления события только один раз.
— вероятность наступления события нуль раз.
Пусть теперь n=3. Тогда возможно наступление одного из следующих вариантов событий:
Соответствующие вероятности равны.
Очевидно, что полученные результаты при n=2 и n=3 являются элементами .
Теперь допустим, произведено n испытаний. Событие А может наступить n раз, 0 раз, n-1 раз и т.д. Напишем событие, состоящее в наступлении события А m раз
Необходимо найти число испытаний, в которых событие А наступит m раз. Для этого надо найти число комбинаций из n элементов, в которых А повторяется m раз, а n-m раз.
— вероятность наступления события А.
Последняя формула называется формулой Бернулли и представляет собой общий член разложения :
Из формулы (1) видно, что ее удобно использовать, когда число испытаний не слишком велико.
№ 1. Бросается монета 7 раз. Найти вероятность наступления орла три раза.
Легко видеть, что пользоваться формулой Бернулли при больших значениях n достаточно трудно, так как формула требует выполнения действий над громадными числами. Естественно, возникает вопрос: нельзя ли вычислить интересующую нас вероятность, не прибегая к формуле Бернулли.
В 1730 г. другой метод решения при p=1/2 нашел Муавр; в 1783 г. Лаплас обобщил формулу Муавра для произвольного p, отличного от 0 и 1.
Эта формула применяется при неограниченном возрастании числа испытаний, когда вероятность наступления события не слишком близка к нулю или единице. Поэтому теорему, о которой идет речь, называют теоремой Муавра-Лапласа.
Теорема Муавра-Лапласа. Если вероятность p появления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность того, что событие А появится в n испытаниях ровно k раз, приближенно равна(тем точнее, чем больше n) значению функции
Имеются таблицы, в которых помещены значения функции
соответствующие положительным значениям аргумента x(см. приложение1). Для отрицательных значений аргумента пользуются теми же таблицами, так как функция четна, т.е. .
Итак, вероятность того, что событие A появится в n независимых испытаниях ровно k раз, приближенно равна
№ 14. Вероятность поражения мишени стрелком при одном выстреле p=0,75.
Найти вероятность того, что при 10 выстрелах стрелок поразит мишень 8 раз.
Решение. По условию n=10; k=8; p=0,75; q=0,25.
Воспользуемся формулой Лапласа:
Вычислим определяемое данными задачи значение x:
По таблице приложения1 находим
Эта формула применяется при неограниченном возрастании числа испытаний, когда вероятность наступления события достаточно близка к 0 или 1.
Таким образом получили формулу:
№ 17. Вероятность изготовления негодной детали равна 0,0002. Найти вероятность того, что среди 10000 деталей только 2 детали будут негодными.
Решение. n=10000; k=2; p=0,0002.
№ 18. Вероятность изготовления бракованной детали равна 0,0004. Найти вероятность того, что среди 1000 деталей только 5 детали будут бракованными.
Решение. n=1000; k=5; p=0,0004.
Теорема . Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна p, абсолютная величина отклонения относительной частоты появления события от вероятности появления события не превысит положительного числа , приближенно равна удвоенной функции Лапласа при :
Доказательство. Будем считать, что производится n независимых испытаний, в каждом из которых вероятность появления события А постоянна и равна p. Поставим перед собой задачу найти вероятность того, что отклонение относительной частоты от постоянной вероятности p по абсолютной величине не превышает заданного числа . Другими словами, найдем вероятность осуществления неравенства
Заменим неравенство (*) ему равносильными:
Умножая эти неравенства на положительный множитель , получим неравенства, равносильные исходному:
Тогда вероятность найдем следующим образом:
Значение функции находится по таблице(см. приложение2).
№ 20. Вероятность того, что деталь не стандартна, p=0,1. Найти вероятность того, что среди случайно отобранных 400 деталей относительная частота появления нестандартных деталей отклонится от вероятности p=0,1 по абсолютной величине не более, чем на 0,03.
Решение. n=400; p=0,1; q=0,9; =0,03. Требуется найти вероятность . Пользуясь формулой
По таблице приложения2 находим . Следовательно, . Итак, искомая вероятность равна 0,9544.
№ 21. Вероятность того, что деталь не стандартна, p=0,1. Найти, сколько деталей надо отобрать, чтобы с вероятностью, равной 0,9544, можно было утверждать, что относительная частота появления нестандартных деталей(среди отобранных) отклонится от постоянной вероятности p по абсолютной величине не более чем на 0,03.
Решение. По условию, p=0,1; q=0,9; =0,03; . Требуется найти n. Воспользуемся формулой
По таблице приложения 2 находим . Для отыскания числа n получаем уравнение . Отсюда искомое число деталей n=400.
№ 22. Вероятность появления события в каждом из независимых испытаний равна 0,2. Найти, какое отклонение относительной частоты появления события от его вероятности можно ожидать с вероятностью 0,9128 при 5000 испытаниях.

Рассмотрим случай многократного повторения одного и того же испытания или случайного эксперимента. Результат каждого испытания будем считать не зависящим от того, какой результат наступил в предыдущих испытаниях. В качестве результатов или элементарных исходов каждого отдельного испытания будем различать лишь две возможности:
1) появление некоторого события А;

2) появление события , (события, являющегося дополнением А)
Пусть вероятность P(A) появления события А постоянна и равна p (0 n q n-x независимо от того, в каком порядке чередуются эти x единиц и n–x нулей.
Все события, заключающиеся в том, что в n испытаниях событие A произошло x раз, а событие произошло n-x раз, являются несовместными. Поэтому для вычисления вероятности объединения этих событий (или суммы этих событий), нужно сложить вероятности всех этих событий, каждая из которых равна p n q n-x . Всего таких событий можно насчитать столько, сколько можно образовать различных последовательностей длины n, содержащих x цифр "1" и n–x цифр "0". Таких последовательностей получается столько, сколькими способами можно разместить x цифр "1" (или n–x цифр "0") на n местах, то есть число этих последовательностей равно
Отсюда получается формула Бернулли:

Pn (x) =

По формуле Бернулли рассчитывается вероятность появления события A "x" раз в n повторных независимых испытаниях, где p – вероятность появления события A в одном испытании, q - вероятность появления события в одном испытании.
Сформулированные условия проведения испытаний иногда называются "схемой повторных независимых испытаний" или "схемой Бернулли"
Число x появления события A в n повторных независимых испытаниях называется частотой.
Пример. Из урны, содержащей 2 белых и 6 черных шаров, наудачу выбирается с возвращением 5 раз подряд один шар. Подсчитать вероятность того, что 4 раза появится белый шар.
В приведенных выше обозначениях n=8; p=1/4; q=3/4; x=5. Искомую вероятность вычисляем по формуле Бернулли:

По формуле Бернулли можно подсчитать вероятности всех возможных частот: x=0,1,2,3,4,5.
Заметим, что если в этой задаче считать, что белых шаров было 20000, а черных 60000, то очевидно p и q останутся неизменными. Однако в этой ситуации можно пренебречь возвращением извлеченного шара после каждой выборки (при не слишком больших значениях x) и считать вероятности всех частот: x=0,1,2. по формуле Бернулли.
Формула Бернулли при заданных числах p и n позволяет рассчитывать вероятность любой частоты x (0 £ x £ n). Возникает естественный вопрос, какой частоте будет соответствовать наибольшая вероятность?
Предположим, что такая частота существует, и попытаемся ее определить из условия, что вероятность этой частоты не меньше вероятности "предыдущей" и "последующей" частот:
Первое неравенство (*) представляется в виде:

,
что эквивалентно или . Отсюда следует:

Решая второе неравенство (1), получим

Таким образом, частота, имеющая наибольшую вероятность (наивероятнейшая частота), определяется двойным неравенством

Если np+p – целое число (тогда и np–q – целое число), то две частоты: x=np–q и x=n p+p обладают наибольшей вероятностью.
Задачи с решениями.
1. Каждый день акции корпорации АВС поднимаются в цене или падают в цене на один пункт с вероятностями соответственно 0,75 и 0,25. Найти вероятность того, что акции после шести дней вернутся к своей первоначальной цене. Принять условие, что изменения цены акции вверх и вниз – независимые события.
Решение. Для того, чтобы акции вернулись за 6 дней к своей первоначальной цене, нужно, чтобы за это время они 3 раза поднялись в цене и три раза опустились в цене. Искомая вероятность рассчитывается по формуле Бернулли

2. Моторы многомоторного самолёта выходят из строя во время полёта независимо один от другого с вероятностью р. Многомоторный самолёт продолжает лететь, если работает не менее половины его моторов. При каких значениях р двухмоторный самолёт надёжней четырёхмоторного самолёта?

Решение. Двухмоторный самолёт терпит аварию, если отказывают оба его мотора. Это происходит с вероятностью р 2 . Четырёхмоторный самолёт терпит аварию, если выходят из строя все 4 мотора а это происходит с вероятностью р 4 , либо выходят из строя три мотора из 4-х. Вероятность последнего события вычисляется по формуле Бернулли: . Чтобы двухмоторный самолёт был надёжнее, чем четырёхмоторный, нужно, чтобы выполнялось неравенство
Это неравенство сводится к неравенству (3р–1)(р–1) 1/3. Следует отметить, что если бы вероятность выхода из строя мотора самолёта превышала одну треть, сама идея использования авиации для пассажирских перевозок была бы очень сомнительной.
3. Бригада из десяти человек идёт обедать. Имеются две одинаковые столовые, и каждый член бригады независимо один от другого идёт обедать в любую из этих столовых. Если в одну из столовых случайно придёт больше посетителей, чем в ней имеется мест, то возникает очередь. Какое наименьшее число мест должно быть в каждой из столовых, чтобы вероятность возникновения очереди была меньше 0,15?

Аннотация: Рассмотрены на примерах Схемы Бернулли повторных испытаний из теории вероятностей, механизмы ее действия и применения в жизни.
Ключевые слова: Теория вероятностей, схемы Бернулли.
Людей всегда интересовало будущее. Человечество во все времена искало способ его предугадать или спланировать: в разное время разными способами. В современном мире есть теория, которую наука признает и пользуется для планирования и прогнозирования будущего. Речь о теории вероятностей.
Теория вероятностей - это математическая наука, изучающая закономерности в случайных явлениях. На сегодняшний день это полноценная наука, имеющая большое практическое значение.
Разумный человек должен стремиться мыслить, исходя из законов вероятностей (статистики). Но в жизни о вероятности мало кто думает. Решения принимаются эмоционально. Люди боятся летать самолетами. А между тем, самое опасное в полете на самолете - это дорога в аэропорт на автомобиле. Но попробуй кому-то объяснить, что машина опасней самолета. Вероятность того, что пассажир, севший в самолет погибнет в авиакатастрофе составляет примерно 1/8 000 000. Если пассажир будет садиться каждый день на случайный рейс, ему понадобится 21 000 лет чтобы погибнуть.
Согласно исследованиям, в США в первые 3 месяца после терактов 11 сентября 2001 года погибло еще одна тысяч людей косвенно. Они в страхе перестали летать самолетами и начали передвигаться по стране на автомобилях. А так как это опасней, то количество смертей возросло. Миром правит вероятность и нужно помнить об этом. Они помогут вам взглянуть на мир с точки зрения случая.
Существует мнение, что решающее влияние на возникновение теории вероятностей оказали азартные игры. Действительно, карты, рулетка, игральные кости, различные лотереи издавна привлекали внимание определенных кругов общества.
Возникновение теории вероятностей как науки относится к середине XVII столетия, когда усилиями Паскаля, Ферма, Гюйгенса были введены специфические понятия и доказаны простейшие теоремы о вероятностях случайных событий.
Важный этап в развитие теории вероятностей связан с именем Я. Бернулли. Теорема, которая носит ныне его имя, вскрывает следующую важную особенность вероятностных задач: рассмотрению подлежат лишь те опыты со случайными исходами, которые независимо друг от друга могут быть повторены любое число раз в одинаковых условиях. Для определенности будем говорить о подбрасываниях монеты. Каждое отдельное подбрасывание монеты приводит к непредсказуемому исходу: выпадает либо герб, либо решка. Если число гербов, выпадающих при n бросаниях монеты, то непредсказуемой является и частота выпадений герба. Однако с ростом n эта непредсказуемость ослабевает: наблюдаемые значения величины имеют тенденцию группироваться около числа 0,5. Отмеченный принцип устойчивости частот выражает одну из важнейших закономерностей случайных явлений.
Своей знаменитой теоремой Бернулли дал математическое истолкование принципа устойчивости частот и закрепил за теорией вероятностей право называться наукой о математических методах изучения закономерностей случайных явлений.
При практическом применении теории вероятностей часто приходится встречаться с задачами, в которых одно и то же испытание повторяется неоднократно. В результате каждого испытания может появиться или не появиться некоторое событие А. Причем нас интересует не результат каждого отдельного испытания, а общее число появлений события А в результате серии опытов. Например, если производится группа выстрелов по одной и той же цели, нас, как правило, не интересует результат каждого выстрела, а лишь общее число попаданий. В подобных задачах требуется уметь определять вероятность любого заданного числа появлений события в результате серии опытов. Такие задачи и будут рассмотрены. Они решаются весьма просто в случае, когда испытания являются независимыми.
Испытания называются независимыми, если вероятность того или иного исхода каждого из испытаний не зависит от того, какие исходы имели другие испытания. Например, несколько бросаний монеты представляют собой независимые испытания.
Я решил проверить классическое определение вероятности.
Возьмем, к примеру, игру в монету. При бросании может быть два равновероятных исхода: монета может упасть кверху гербом или решкой. Бросая монету один раз нельзя предугадать, какая сторона окажется сверху. Однако, бросив монету 100 раз, можно сделать выводы. Можно заранее сказать, что герб выпадет не 1 и не 2 раза, а больше, но и не 99 и не 98 раз, а меньше. Число выпадений герба будет близко к 50. На самом деле, и на опыте можно в этом убедиться, что это число будет заключено между 40 и 60. Кто и когда впервые проделал опыт с монетой, неизвестно.
Проведём опыт. Для начала, возьмем в руки монетку, будем ее бросать и записывать результат последовательно в виде строки: О, Р, Р, О, О, Р. Здесь буквами О и Р обозначено выпадение орла или решки. В нашем случае бросание монетки - это испытание, а выпадение орла или решки - событие, то есть возможный исход нашего испытания. В процессе проведения 100 испытаний орел выпал 55 раз, решка - 45. Вероятность выпадения орла в данном случае-0,55; решки – 0,45. Таким образом, я показал, что теория вероятности в данном случае имеет место быть.
Можно ли выиграть в лотерею или рулетку?
Каждый из нас хоть раз в жизни покупал лотерею или играл в азартные игры, но далеко не все использовали заранее спланированную стратегию. Умные игроки давно перестали надеяться на удачу и включили рациональное мышление.
Дело в том, что каждое событие имеет определенное математическое ожидание, как гласят высшая математика и теория вероятности, и, если правильно оценивать ситуацию, то можно обойти неудовлетворительный исход события.
Повторные независимые испытания называются испытаниями Бернулли, если каждое испытание имеет только два возможных исхода и вероятности исходов остаются неизменными для всех испытаний.
Приведу пример практического применения схемы испытаний Бернулли на примере нашего института. На I курс ТИЖТа в 2016г. поступило 295 студентов. Требуется найти наиболее вероятное число первокурсников, родившихся в один день, день знаний 1-го сентября, и вероятность этого события.
Решение. В нашем случае р= 1:365 n=295 Используем соотношение для наивероятнейшего числа: m0
295*(1:365)-(364:365)m0295*(1:365)+(1:365)
Учитывая, что m0 целое число, получаем m0= 1.
Найдем теперь P295(1), используя теорему Пуассона и то, ƛ=295*(1:365)
Приведу следующий пример практического применения схемы испытаний Бернулли. Колёсные пары, изготовляемые при массовом производстве, могут отличаться по толщине, но при проверке они классифицируются на годные и дефектные - в зависимости от того, находится ли толщина в предписанных границах. И хотя продукция по многим причинам не может вполне соответствовать схеме Бернулли, эта схема задает идеальный стандарт для промышленного контроля качества продукции, несмотря даже на то, что этот стандарт никогда не достигается вполне точно. Вагоны подвержены изменениям, и поэтому вероятности не остаются одними и теми же. В режиме эксплуатации вагонов имеется некоторое постоянство, в результате чего длинные серии одинаковых отклонений оказываются более вероятными, чем это было бы при действительной независимости испытаний. Однако с точки зрения контроля качества продукции желательно, чтобы процесс соответствовал схеме Бернулли, и важно то, что в некоторых пределах этого можно добиться. Целью текущего контроля является обнаружение уже на ранней стадии существенных отступлений от идеальной схемы и использование их как указаний на угрожающее нарушение правильности эксплуатации вагонов.
Можем ли мы предугадать с помощью этой теории, что случится с нами через день, два, тысячу? Конечно, нет. Событий, связанных с нами в каждый момент времени, очень много. Только на одну лишь типизацию этих событий не хватит и жизни. А уж их совмещение и вовсе гиблое дело. С помощью Схемы Бернулли предугадывать можно лишь однотипные события. Например, такое как бросание монеты - это событие из 2 вероятностных результатов. В общем, прикладное применение теории вероятностей связанно с немалым количеством условий и ограничений, а для сложных процессов сопряжено с вычислениями, которые под силу лишь компьютеру.
Таким образом, работаем над собой, принимаем решения, которые могут повысить вероятность выполнения наших желаний и стремлений, каждый случай может добавить те заветные 0.00001, которые сыграют решающую роль в итоге.
В заключение хочется отметить то, что распределение Бернулли является достаточно распространенным и важным распределением, имеющим применение как в теории вероятностей и ее приложениях, так и в математической статистике.
Вы можете изучить и скачать доклад-презентацию на тему Схема Бернулли. Презентация на заданную тему содержит 25 слайдов. Для просмотра воспользуйтесь проигрывателем, если материал оказался полезным для Вас - поделитесь им с друзьями с помощью социальных кнопок и добавьте наш сайт презентаций в закладки!
























На дне глубокого сосуда Лежат спокойно n шаров. Поочередно их оттуда Таскают двое дураков. Сия работа им приятна, Они таскают t минут, И, вынув шар, его обратно Тотчас немедленно кладут. Ввиду занятия такого, Сколь вероятность велика, Что первый был глупей второго, Когда шаров он вынул k? В. П. Скитович
27 декабря 1654, Базель, — 16 августа 1705, там же — швейцарский математик, старший брат Иоганна Бернулли; профессор математики Базельского университета (с 1687 года). 27 декабря 1654, Базель, — 16 августа 1705, там же — швейцарский математик, старший брат Иоганна Бернулли; профессор математики Базельского университета (с 1687 года).
При n независимых повторений одного и того же испытания с двумя возможными исходами более кратко говорят как об n испытаниях Бернулли При n независимых повторений одного и того же испытания с двумя возможными исходами более кратко говорят как об n испытаниях Бернулли
Каждый из 4 приятелей выучил ровно 5 вопросов из 20 заданных к зачету. На зачете они отвечали в разных аудиториях и получали вопросы независимо друг от друга. Найти вероятность того, что: Каждый из 4 приятелей выучил ровно 5 вопросов из 20 заданных к зачету. На зачете они отвечали в разных аудиториях и получали вопросы независимо друг от друга. Найти вероятность того, что: а) каждому достался тот вопрос, который он выучил; б) никому не достался вопрос, который он выучил; в) только одному достался вопрос, который он не выучил; г) хотя бы одному достался вопрос, который он выучил.
Вероятность того, что стрелок поразит мишень при одном выстреле, равна 0,4. Стрелок производит независимо 5 выстрелов. Составить таблицу распределения вероятностей числа попаданий. Найти вероятность того, что стрелок ни разу не промахнется. Вероятность того, что стрелок поразит мишень при одном выстреле, равна 0,4. Стрелок производит независимо 5 выстрелов. Составить таблицу распределения вероятностей числа попаданий. Найти вероятность того, что стрелок ни разу не промахнется.
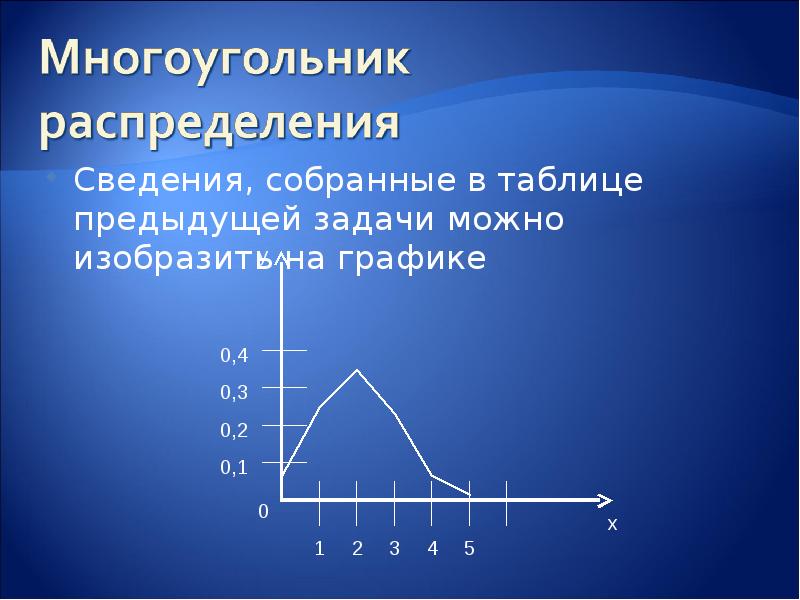
По условию, n=5; p=0,4; q=0,6; k=0,1,2,3,4,5: По условию, n=5; p=0,4; q=0,6; k=0,1,2,3,4,5: P5(0)=C0p0q5=0,65≈0,078; P5(1)=C1pq4=5*0,4*0,64 ≈0,259; P5(2)=C2p2q3=10*0,42*0,63 ≈0,346; P5(3)=C3p3q2=10*0,43*0,62 ≈0,23; P5(4)=C1p4q=5*0,44*0,6 ≈0,077; P5(5)=C5p5q0=0,45≈0,01.
Сведения, собранные в таблице предыдущей задачи можно изобразить на графике Сведения, собранные в таблице предыдущей задачи можно изобразить на графике
Ломаную, соединяющую отмеченные на графике точки, называют многоугольником распределения. Ломаную, соединяющую отмеченные на графике точки, называют многоугольником распределения.
Последовательность чисел Pn(0), Pn(1), Pn(2),…, Pn(k),…, Pn(n-1), Pn(n) сначала возрастает, а затем, приняв наибольшее значение, убывает. Только в некоторых специальных случаях наибольшее значение достигается не для одного, а для двух соседних значений k. Можно доказать, что вероятность Pn(k) принимает наибольшее значение при значении k, равном ближайшему к np-q справа целому числу. Если же само число np-q целое, то наибольшее значение вероятность принимает для двух значений k: для k=np-q и для k=np+p. Последовательность чисел Pn(0), Pn(1), Pn(2),…, Pn(k),…, Pn(n-1), Pn(n) сначала возрастает, а затем, приняв наибольшее значение, убывает. Только в некоторых специальных случаях наибольшее значение достигается не для одного, а для двух соседних значений k. Можно доказать, что вероятность Pn(k) принимает наибольшее значение при значении k, равном ближайшему к np-q справа целому числу. Если же само число np-q целое, то наибольшее значение вероятность принимает для двух значений k: для k=np-q и для k=np+p.
Найти наивероятнейшее число выпадений решки при: а) 100 бросаниях монеты; б) 1001 бросании монеты. Найти наивероятнейшее число выпадений решки при: а) 100 бросаниях монеты; б) 1001 бросании монеты.
а) В данном случае n=100, p=q=0,5. Тогда число np-q=100*0,5-0,5=49,5 – не целое. Ближайшее к нему справа целое число равно 50. Оно равно половине числа всех бросаний и является наивероятнейшим числом выпадений решки. а) В данном случае n=100, p=q=0,5. Тогда число np-q=100*0,5-0,5=49,5 – не целое. Ближайшее к нему справа целое число равно 50. Оно равно половине числа всех бросаний и является наивероятнейшим числом выпадений решки. б) в данном случае n=1001, p=q=0,5. Тогда число np-q=1001*0,5-0
Читайте также:

