Реферат поле скоростей и линии трубки тока
Обновлено: 05.07.2024
В отличие от кинематики отдельной точки или системы конечного числа точек механика сплошной среды имеет свои специфические приемы задания движения.
Ближе всего к обычным способам задания движения подходит способ, связанный с именем Лагранжа.
Пусть некоторая частица жидкости или газа в момент времени занимала положение тогда ее координаты в любой момент можно рассматривать как функции от времени и параметров определяющих выбор данной индивидуальной частицы Более обще, вместо декартовых координат точки можно рассматривать любые ее криволинейные координаты связанные с соотношениями:
Положение любой частицы жидкости в момент времени задается выражениями ее декартовых координат через величины называемые переменными Лагранжа:
Задавая определенные значения параметрам получим обычные, принятые в кинематике точки уравнения движения данной индивидуальной частицы жидкости, откуда уже нетрудно найти уравнения траектории частицы и выражения проекции вектора ее скорости и ускорения
Производную по времени, вычисляемую в переменных Лагранжа для индивидуально движущейся частицы жидкости, называют индивидуальной или еще субстанциональной (относящейся к определенной частице субстанции).
Другой, получивший более широкое применение прием задания движения среды, предложенный Эйлером, заключается в выражении скоростей частиц в функции от времени и координат х, у, z точек пространства, т. е. в задании поля скоростей. Совокупность величин , называют переменными Эйлера, движение среды, по Эйлеру, задается так:
В методе Лагранжа величины являются переменными координатами одной и той же движущейся частицы жидкости, в методе Эйлера — это координаты точек пространства, мимо которых проходят различные частицы жидкости. Рассмотрим подробнее метод Эйлера, которым, по преимуществу, и будем пользоваться.
Векторные линии поля скоростей, т. е. такие линии, в каждой точке которых скорость в данный момент направлена по касательной к ним, называются линиями тока. Следующий простой опыт даст наглядное представление о линиях тока. Предположим, что на поверхность воды в канале насыпан легкий и хорошо видимый порошок, частицы которого будут двигаться вместе с потоком, не опережая и не отставая от частиц воды. Тогда на фотографии, произведенной с малым временем экспозиции, каждая частичка порошка изобразится в виде небольшой черточки, а черточки эти сольются в отчетливо видимые линии, которые и будут линиями тока в момент производства снимка.
По самому определению, линия тока поля не совпадает с траекторией частицыпредставляющей пространственный след движущейся во времени частицы. Составим дифференциальные уравнения линии тока.
По общему уравнению векторной линии (7) будем иметь следующую систему двух обыкновенных дифференциальных уравнений:
причем разыскиваются конечные связи между переменными а время играет роль фиксированного параметра; величины же представляют проекции произвольного бесконечно малого отрезка направленного вдоль линии тока.
В противоположность этому, проекции направленного элемента траектории представляют проекции перемещения частицы
жидкости за время
отсюда получаем систему трех обыкновенных дифференциальных уравнений траектории:
причем в этой системе уравнений координаты являются неизвестными функциями одного аргумента — времени.
Сравнивая уравнения (34) и (35), видим, что они принципиально отличаются друг от друга, а следовательно, линии тока и траектории не совпадают. Исключение представляет случай стационарного поля, т. е. случай, когда время не входит явно в задание скоростного поля (33). В этом случае уравнения (34) совпадут с уравнениями (35), если в этих уравнениях откинуть дифференциал времени не входящего явно при стационарном движении в остальные уравнения системы (35). Отсюда следует, что при стационарном движении, т. е. движении со стационарным полем скоростей, линии тока совпадают с траекториями.
К этому результату легко придти и из геометрических соображений.
На рис. 6 показаны построения линии тока и траектории проходящих через одну и ту же точку Для построения линии тока фиксируем время и проводим вектор V скорости точки откладываем на нем малый отрезок через точку проводим вектор скорости соответствующий
тому же моменту времени, на векторе откладываем отрезок и скорость точки и т. д., причем все это делаем в один и тот же фиксированный момент времени. При построении траектории вновь отмечаем скорость точки пользуясь произволом в выборе интервала времени, откладываем на ней отрезок по прошествии времени если поле не стационарно, скорость V точки несмотря на совпадение точки с точкой уже не будет равна скорости V, точки в момент Следовательно, траектория отклонится от линии тока, и кривые разойдутся в пространстве. Если же поле стационарно, то, несмотря на то, что время изменилось на скорости совпадающих точек будут одинаковы, точки и так же как их скорости, совпадут, и траектория ничем не будет отличаться от линии тока.
Векторная трубка, образованная линиями тока, называется трубкой тока; часть пространства, ограниченная траекториями частиц, образующих в некоторый момент замкнутый контур, называется струей. Из предыдущего следует, что при стационарном движении трубка тока и струя, выходящие из одного и того же замкнутого контура, совпадают.
Гидродинамика – раздел физики жидкости, в котором изучается движение несжимаемых жидкостей и их взаимодействие с твёрдыми телами.
Существуют два метода описания движения жидкостей:
- метод Лагранжа, который связан с описанием каждой частицы жидкости с помощью функций времени;
- метод Эйлера, который связан с наблюдением отдельных точек пространства, заполненных жидкостью и фиксацией скорости прохождения через данные точки пространства отдельных частиц жидкости.
Состояние жидкости можно определить, указав для каждой точки пространства вектор скорости . Совокупность этих векторов образуют поле вектора . Касательная, проведённая из точек начала векторов и совпадающая с вектором, называется линией тока (рисунок 5.1).
Рисунок 5.1 – Трубка тока с линиями тока
Количеством линий , проходящих через площадку , определяется густота линий тока. Будем считать, что густота линий тока пропорциональна величине скорости течения , т.е. там, где скорость течения жидкости больше, там больше густота линий тока. При условии течение называется установившемся или стационарным.
Часть жидкости, ограниченная линиями тока называется трубкой тока.
Пусть через сечение течёт жидкость в течение времени . Тогда за время через данное сечение проходит объём жидкости равный . Если взять два разных сечения, имеющие площади и , будет наблюдаться следующее. Поскольку жидкость несжимаема и её плотность постоянна во всех точках, то в единицу времени через оба сечения пройдёт одинаковое количество жидкости по объёму, т.е.
Таким образом, для несжимаемой жидкости выполняется условие:
Выражение (5.2) является аналитической записью теоремы о неразрывности струи (рисунок 5.2).
Рисунок 5.2 – Прохождение жидкости через а) сечение за время ; б) разные сечения и
При изменении площади сечения частицы несжимаемой жидкости движутся с ускорением. Если взять трубку тока, то данное ускорение вызвано только непостоянством давления вдоль оси трубки. Там где скорость частиц меньше, давление должно быть больше и наоборот.
5.2 Уравнение Бернулли
Жидкость, в которой нет внутреннего трения, называется идеальной.
Рассмотрим трубку тока, изображенную на рисунке 5.3.
Рисунок 5.3 – Трубка тока с разными поперечными сечениями
В силу неразрывности струи, заштрихованные объёмы и будут равны . Если выполняются условия и , то выражение для приращения энергии струи будет иметь вид:
Приращение энергии должно быть равно только работе, совершаемой силами давления, т.к. трение отсутствует. Силы давления на боковую поверхность направлены перпендикулярно струе, поэтому их работа равна нулю. Работа сил давления, приложенных к сечениям и , равна
Приравниваем правые части выражений (5.3) и (5.4) и, сокращая на , получаем
После преобразований получаем окончательный вид выражения:
Таким образом, в стационарно текущей идеальной жидкости вдоль любой линии тока выполняется условие
Выражение (5.6) является уравнением Бернулли.
Для горизонтальной линии тока, где выполняется условие , выражение (5.5) приобретает упрощённый вид
а уравнение Бернулли записывается:
Таким образом, давление оказывается меньше там, где выше скорость течения.
5.3 Истечение жидкости из отверстия
В случае истечения жидкости из небольшого отверстия в широком открытом сосуде (рисунок 5.4) уравнение Бернулли запишется в следующем виде:
В выражении (5.9) величина означает скорость истечения жидкости из отверстия.
Пусть высота жидкости над отверстием определяется как
Выразим скорость , получим формулу Торричелли:
Рисунок 5.4 – Истечение жидкости из отверстия в широком открытом сосуде
Как показано на рисунке 5.5, струя жидкости, вытекающая из отверстия в сосуде, уносит с собой за время импульс величиной
Главная цель книги — познакомить студентов прежде всего с основными идеями и методами физики. Особое внимание обращено на разъяснение смысли физических законов и на сознательное применение их. Несмотря на сравнительно небольшой объем, книга представляет собой серьезное руководство, обеспечивающее подготовку, достаточную для успешного усвоения в дальнейшем теоретической физики и других физических дисциплин.
Предисловие к четвертому изданию
При подготовке к настоящему изданию книга была значительно переработана. Написаны заново (полностью или частично) параграфы 7, 17, 18, 22, 27, 33, 36, 37, 40, 43, 68, 88. Существенные добавления или изменения сделаны в параграфах 2, 11, 81, 89, 104, 113.
Ранее, при подготовке ко второму и третьему изданиям были написаны заново параграфы 14, 73, 75. Существенные изменения или добавления были внесены в параграфы 109, 114, 133, 143.
Таким образом, по сравнению с первым изданием облик первого тома заметно изменился. Эти изменения отражают методический опыт, накопленный автором последние десять лет преподавания обшей физики в Московском инженерно-физическом институте.
Ноябрь 1969 г. И. Савельев
Из предисловия к четвертому изданию
Предлагаемая вниманию читателей книга представляет собой первый том учебного пособия по курсу общей физики для втузов. Автор в течение ряда лет преподавал общую физику в Московском инженерно-физическом институте. Естественно поэтому, что пособие он писал имея в виду прежде всего студентов инженерно-физических специальностей втузов.
При написании книги автор стремился познакомить учащихся с основными идеями и методами физической науки, научить их физически мыслить. Поэтому книга не является по своему характеру энциклопедичной, содержание в основном посвящено тому, чтобы разъяснить смысл физических законов и научить сознательно применять их. Не осведомленности читателя по максимально широкому кругу вопросов, а глубоких знаний фундаментальным основам физической пауки — вот что стремился добиться автор.
При кинематическом описании движения любой механической системы нет необходимости подробно рассматривать внутренние физические свойства тел, включенных в систему (рис. 174).

При описании движения жидкости достаточно принять во внимание ее текучесть − способность изменять свою форму при малейшем внешнем воздействии. Свойства жидкостей и газов существенно различаются, однако описание движения жидкостей и газов сходно, поэтому в данном разделе, говоря об описании движения жидкости, будем иметь в виду, что описание движения газов проводится аналогично.
При движении жидкости можно проследить, что происходит с течением времени в каждой ее точке, т.е. можно указать величину и направление скорости движения различных частиц жидкости, которые в разные моменты времени проходят через одну и ту же точку пространства. При фиксированном времени в пространстве возникает мгновенная картина распределения скоростей жидкости - поле скоростей.
Следовательно, в каждой точке пространства можно указать вектор скорости любой частицы, проходящей через эту точку в данный момент времени.
Векторным полем называют область пространства, в каждой точке которой задано значение вектора a(r). Графически изображение векторного поля осуществляется с помощью векторных линий. Вектор a(r) является вектором касательной к векторной линии в точке Густота векторных линий пропорциональна абсолютному значению |r|.
Наглядно представить себе векторное поле достаточно затруднительно − в каждой точке необходимо изобразить вектор, что, конечно, невозможно. Поэтому используются несколько упрощенных способов графического представления векторных полей. Наиболее часто встречается изображение векторных с помощью линий поля − линий, касательные к которым совпадают с вектором поля (рис. 175).

В рассматриваемом случае поля скоростей − линии поля называются линиями тока. Линия тока − такая линия, касательная к которой в каждой точке совпадает с направлением вектора скорости в данной точке. На линиях тока принято указывать направление движения жидкости. Заметим, что линию тока можно провести через любую точку, поэтому число линий, их густота определяются исключительно эстетическими соображениями.
Семейство линий тока достаточно наглядно представляет движение жидкости в некоторой области (рис. 176).
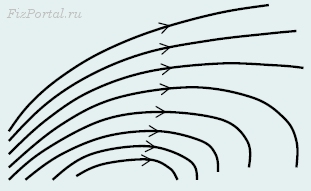
Исходя из определения, можно установить их общие свойства:
1. Линии тока не пересекаются (в противном случае в точке пересечения можно построить две касательные, то есть в одной точке скорость жидкости имеет два значения, что абсурдно).
2. Линии тока не имеют изломов (в точке излома опять можно построить две касательные).
3. Линии тока начинаются на источниках и заканчиваются на точках стока жидкости.
Если поле скоростей и соответствующие ему линии тока, не изменяются с течением времени, то движение жидкости называют стационарным.
Если движение жидкости является стационарным, то линии тока совпадают с траекториями движения частиц жидкости. В нестационарном потоке линии тока изменяются с течением времени, поэтому траектория отдельно взятой частицы отличается от линии тока. В этом случае линии тока следует рассматривать как вспомогательные математические иллюстрации, не имеющие явного физического смысла.
Рассмотрим произвольный замкнутый контур L, в котором через каждую его точку, в один и тот же момент времени, проведены линии тока (рис. 6.4). Они образуют поверхность, называемую трубкой тока.
Рис. 6.4
Скорости частиц жидкости направлены по касательным к линиям тока и при течении жидкости они не пересекают боковой поверхности трубки тока. На такие трубки тока можно разбить все пространство, занимаемое жидкостью. Если поперечное сечение трубки тока бесконечно мало, то скорость частиц жидкости будет направлена вдоль оси трубки тока.
Массу жидкости, протекающую через поперечное сечение трубки тока за время dt, можно определить по формуле
где r - плотность жидкости; S - площадь поперечного сечения трубки тока, нормально расположенной к линиям тока.
Для всех сечений трубки тока при стационарном течении жидкости dm=сonst. Для двух произвольных поперечных сечений трубки тока S1 и S2 (рис. 6.4) выполняется равенство
| r1v1S1 = r2v2S2. | (6.19) |
Если жидкость несжимаема, то r1= r2,
тогда формула (6.19) принимает вид
т.е. скорость течения жидкости обратно пропорциональна площади поперечного сечения трубки тока.
Траектория – это линия, изображающая путь пройденный частицей за определенный промежуток времени.
Линия тока – это мгновенная векторная линия, в каждой точке которой в данный момент времени касательная по направлению совпадает с вектором скорости.

В стационарных задачах линии тока и траектории совпадают, т.к. нормальная составляющая скорости к линии тока равна нулю, жидкость через линию тока не перетекает. В плоских течениях количество жидкости между двумя линиями тока в любых сечениях будет одинаково. Если линии тока приближаются, то скорость потока увеличивается, и наоборот. Через каждую точку в потоке можно провести только одну линию тока, исключение составляют особые точки: критические точки. А и В – это критические точки. Поверхность непроницаемого тела – поверхность тока, а линии тока, расположенные на поверхности называется нулевыми линиями тока.
Если в жидкости провести замкнутый контур и через каждую точку провести линию тока, получим поверхность тока. Жидкость внутри поверхности называется трубкой тока. Через поверхность тока жидкость не перетекает, следовательно через каждое сечение трубки тока проходит одно и то же количество жидкости. Если через каждую точку контура провести траекторию, то часть жидкости, которая ограничена поверхностью траектории называется струей. Струя совпадает с трубкой тока в стационарном течении.
4. Градиент, дивергенция, циркуляция, вихрь
Рассмотрим действие векторного оператора Гамильтона на скалярную функцию φ. Скалярная величина – это параметр, которому нельзя придать направление.

Градиент скалярной функции – это вектор направленный по нормали к линии постоянного значения в сторону возрастания функции и модуль его равен частной производной от функции по направлению указанной нормали.
Рассмотрим скалярное умножение векторного оператора и двух величин скорости:

Дивергенция является скалярной величиной, показывает расхождение вектора скорости, определяет закон относительного изменения объема. Например, если течение стационарное и жидкость несжимаемая, то при в жидкости отсутствуют источники или стоки. При имеется источник, при имеется сток. Уравнение часто используется для замыкания системы уравнений движения несжимаемой жидкости и является уравнением сплошности.
Характеризует интенсивность вращательного движения жидкости.
Вычисляется, например, по контуру АВ:



- элемент контура АВ
4. Вихрь вектора скорости.
Рассмотрим векторное произведение оператора на вектор скорости:




Рассмотрим вращение точки вокруг оси, проходящей через начало координат с угловой скоростью .





Если в жидкости , это указывает на наличие вращающихся объемов, вихрей жидкости. Интерес представляют течения для которых , такие течения называются безвихревыми или потенциальными,. Т.к. в этом случает существует потенциал вектора скорости φ, который связан с составляющими вектора скорости следующими соотношениями:
Читайте также:

