Реферат по геометрии 7 класс

Обновлено: 05.07.2024

Треуго́льник — простейший многоугольник, имеющий 3 угла (вершины) и 3 стороны; часть плоскости, ограниченная точками тремя, и тремя отрезками, попарно соединяющими точки эти.

Если все три точки лежат треугольника на одной прямой, он называется вырожденным.

1. особенности и Свойства треугольников

Трём точкам пространства, не одной на лежащим прямой (и образуемому ими невырожденному обязательно), треугольнику соответствует одна и только одна Это. плоскость весьма уникально — так как количеству меньшему точек соответствуют прямая и точка, а четыре уже точки могут находится вне плоскости единой. [1]

Треугольник — это часть плоскости, минимально ограниченная возможным количеством сторон. Любой можно многоугольник точно разбить на треугольники, лишь его связав вершины отрезками, не пересекающими его некоторым. С стороны приближением, на треугольники можно разбить любой поверхность формы, как на плоскости так и в Процесс. пространстве разбиения на треугольники называется триангуляция.

раздел Существует математики, целиком посвящённый изучению треугольников закономерностей — Тригонометрия.

Треугольник, когда не вырожден — выпуклый всегда многоугольник.

Для треугольника всегда одна существует вписанная и одна описанная окружность.

2. Поскольку

Обозначения сумма углов треугольника равна менее°, то не 180 двух углов в треугольнике должны острыми быть (меньшими 90°). Выделяют следующие виды Если:

треугольников все углы треугольника острые, то называется треугольник остроугольным;
Если один из углов тупой треугольника (больше 90°), то треугольник называется тупоугольным;
один Если из углов треугольника прямой (равен 90°), то называется треугольник прямоугольным. Две стороны, образующие угол прямой, называются катетами, а сторона, противолежащая углу прямому, называется гипотенузой.

4.2. По числу равных Разносторонним

сторон называется треугольник, у которого длины сторон трёх различны.
Равнобедренным называется треугольник, у две которого стороны равны. Эти стороны боковыми называются, третья сторона называется основанием. В треугольнике равнобедренном углы при основании равны. медиана, Высота и биссектриса равнобедренного треугольника, опущенные на совпадают, основание.
Равносторонним называется треугольник, у которого три все стороны равны. В равностороннем треугольнике углы все равны 60°, а центры вписанной и описанной совпадают окружностей.

5. Определения, связанные с треугольником

5.1. Окружности

окружность Вписанная — окружность, касающаяся всех трёх треугольника сторон. Она единственна. Центр вписанной называется окружности инцентром.
Описанная окружность — окружность, через проходящая все три вершины треугольника. окружность Описанная также единственна.
Вневписанная окружность — касающаяся, окружность одной стороны треугольника и продолжения других двух сторон.

5.2. Лучи, отрезки и точки

треугольника Медианой, проведённой из данной вершины, называется соединяющий, отрезок эту вершину с серединой противолежащей основанием (стороны медианы). Все три медианы пересекаются треугольника в одной точке. Эта точка называется пересечения

треугольника Высотой, проведённой из данной вершины, называется опущенный, перпендикуляр из этой вершины на противоположную сторону продолжение её или. Три высоты треугольника пересекаются в точке одной, называемой ортоцентром треугольника.

Биссектрисой проведённой, треугольника из данной вершины, называют отрезок, эту соединяющий вершину с точкой на противоположной стороне и угол делящий при данной вершине пополам. треугольника Биссектрисы пересекаются в одной точке, и эта совпадает точка с центром вписанной окружности (инцентром).

линией Средней треугольника называют отрезок, соединяющий двух середины сторон этого треугольника.

В равнобедренном биссектриса треугольнике, медиана и высота, проведённые к основанию, Верно. совпадают и обратное: если биссектриса, медиана и проведённые, высота из одной вершины, совпадают, то треугольник Если. равнобедренный треугольник разносторонний, то для любой вершины его биссектриса, проведённая из неё, лежит медианой между и высотой, проведёнными из той же вершины.

перпендикуляры Серединные(медиатриссы) к сторонам треугольника также одной в пересекаются точке, которая совпадает с центром окружности описанной.

Середины трёх сторон треугольника, трёх основания его высот и середины трёх соединяющих, отрезков его вершины с ортоцентром, лежат на окружности одной, называемой окружностью девяти точек.

В треугольнике любом центр тяжести, ортоцентр, центр окружности описанной и центр окружности девяти точек одной на лежат прямой, называемой прямой Эйлера.

инцентр, Ортоцентр, центроид (центр тяжести), а также другие некоторые точки называются замечательными точками Соотношения.

6. треугольника в треугольнике

6.1. Неравенство треугольника

В невырожденном сумма треугольнике длин двух его сторон длины больше третьей стороны, в вырожденном — равна. говоря Иначе, длины сторон невырожденного треугольника следующими связаны неравенствами.

6.2. Теорема о сумме углов Теорема

6.3. треугольника синусов

где R — радиус окружности, вокруг описанной треугольника. Из теоремы следует, что Теорема a 6.4. если косинусов

Является обобщением теоремы Прочие.

6.5. Пифагора соотношения

Метрические соотношения в треугольнике для приведены треугольника
:

a_L,b_L — которые, на отрезки биссектриса
делит сторону
,
m_a,m_b,m_c — медианы, соответственно проведённые к сторонам a , b и c ,
h_a,h_b,h_c — высоты, опущенные соответственно на радиус a , b и c ,
r — стороны вписанной окружности,
R — радиус описанной полупериметр,
— окружности,
S — площадь,
d — расстояние между центрами описанной и вписанной окружностей.

7. Площадь треугольника

Для площади справедливы неравенства:

, оба причём равенства достигаются.
, где равенство для достигается равнобедренного прямоугольного треугольника.

7.1. Вычисление треугольника площади в пространстве с помощью векторов

Пусть треугольника вершины находятся в точках
, , .

Введём вектор Длина
. площади этого вектора равна площади направлен, а треугольника он по нормали к плоскости треугольника:

Положим
, проекции
, , — где треугольника на координатные плоскости. При аналогично

Площадь треугольника равна
.

Альтернативой вычисление служит длин сторон (по теореме Пифагора) и формуле по далее Герона.

скачать
Данный реферат основе на составлен статьи из русской Википедии. Синхронизация Похожие 11.07.11 08:54:04

Для учеников 1-11 классов и дошкольников
Бесплатные сертификаты учителям и участникам

Министерство образования Республики Башкортостан

Муниципальное бюджетное образовательное учреждение

Средняя общеобразовательная школа №8 г. Бирска муниципального района

Бирский район Республики Башкортостан

Геометрические построения

Ученица 7класса

Иванова Кристина

Руководитель:

учитель математики

Янсыбина Л. А.

Бирск 2017г.

1. Геометрия как наука .

2. Зачем в геометрии построения.

3. Задачи на построение.

4. Деление отрезка и окружности.

Задачи на построения в геометрии

Задачи на построение вошли в практику задолго до того, как геометрия и вообще математика стала настоящей теоретической наукой. И в Вавилоне, и в Древнем Египте в IV-II тысячелетиях до н.э. уже существовала практическая математика (в виде правил записи чисел, т.е. системы счисления, и правил различных вычислений), и практическая геометрия - геометрия в изначальном смысле слова: измерение земли. Но и при измерениях, и при строительных работах нужны были построения. Египтяне, по-видимому, знали, что треугольник со сторонами 3, 4, 5 - прямоугольный, так что с помощью веревки, разделенной узлами на 12 = 3 + 4 + 5 частей, можно построить прямой угол. Древние греки так и называли египетских геометров "гарпедонаптами" - дословно, "натягивателями веревок". С другой стороны, уже вавилоняне рассматривали геометрические задачи теоретического характера, использовали подобие фигур, знали "теорему Пифагора" более чем за тысячу лет до Пифагора. Однако математические и геометрические знания в Вавилоне, Египте, да и в Греции вплоть до VII в. до н.э. были эмпирическими, основанными только на опыте и наблюдениях.

Геометрия как наука, да и вообще наука как таковая, появилась во времена Фалеса (VII-VI вв. до н.э.), который впервые осознал необходимость доказательства математических теорем. После Аристотеля (IV в. до н.э.) название "геометрия" закрепилось за математической наукой, а "землемерию" было дано свое наименование: "геодезия" - деление, межевание земель. К концу IV века до н.э. в математике, которая и сводилась, главным образом, к геометрии, накопилось много понятий, фактов, доказательств, методов и даже теорий - таких, как метод исчерпывания и теория отношений Евдокса, теория конических сечений и др. Аристотелем уже были разработаны основные принципы построения общей аксиоматической теории. И на рубеже IV и III веков Евклид создал 13-томный труд, "Stoicheia" - стихии, элементы по-гречески, "Elementa" (элементы) на латыни, "Начала" по-русски. "Начала" вот уже третье тысячелетие служат образцом научного трактата (аксиоматического изложения теории) и учебника, и не только по геометрии

Зачем Евклиду потребовались построения? Зачем вообще в геометрии построения? Зачем нужно учиться решать задачи на построение (Евклид называл их проблемами, в отличие от теорем)?

Доказательства, да и вычисления в геометрии, как правило, опираются на какие-то дополнительные построения. Конечно, их можно просто описать, но нужно быть уверенными, что они действительно возможны. Еще важнее то, что определения геометрических объектов и понятий при строгом изложении теории должны сопровождаться доказательствами их существования. А главный метод доказательства существования в геометрии - конструктивный, т. е. построение нужного объекта с последующим доказательством, что построенный объект удовлетворяет нужным условиям.

Решение задач на построение развивает геометрическое мышление гораздо полнее и острее, чем решение задач на вычисление, и способно вызвать увлечение работой, которое приводит к усилению любознательности и к желанию расширить и углубить изучение геометрии.

Несмотря на богатое историческое прошлое, проблема решения задач на построение остается актуальной и в 21-м веке. В наше время бурно развиваются компьютерные технологии с применением графических редакторов для рисования геометрических объектов. Средства создания геометрических объектов изменились в связи с появлением новых компьютерных технологий. Однако, как и в глубокой древности, основными элементами при построении геометрических объектов остаются окружность и прямая, другими словами циркуль и линейка. С появлением новых компьютерных технологий возникли новые проблемы построения с использованием тех же объектов - прямой и окружности. Вот почему проблема решения задач на построение становится ещё более актуальной.

Инструменты, употребляемые для выполнения геометрических построений, весьма разнообразны. К основным инструментам принадлежат линейка и циркуль, служащие для проведения прямых линий, одиночных, параллельных и перпендикулярных, и окружностей. Угольник есть вспомогательный инструмент, так как, имея линейку и циркуль, можно строить параллельные и перпендикулярные прямые. К вспомогательным инструментам относится также миллиметровая шкала, которую можно построить с помощью циркуля и линейки, отложив на прямой линии циркулем одинаковые сантиметровые отрезки и разделив каждый из этих отрезков на 10 равных между собою частей. Транспортир есть уже самодеятельный инструмент, так как точное в геометрическом смысле градуирование любой дуги на произвольное число равных частей с помощью линейки и циркуля невозможно.

С глубокой древности повелось допускать к исполнению геометрических построений только циркуль и линейку, т. е. приборы, позволяющие проводить прямые линии и окружности. В задачах на построение циркуль и линейка предполагаются идеальными инструментами, в частности:

Линейка не имеет делений и имеет сторону бесконечной длины, но только одну.

Циркуль может иметь какой угодно большой или малый раствор (то есть может чертить окружность произвольного радиуса).

С помощью циркуля можно провести произвольную окружность, можно провести окружность с данным центром и данного радиуса. Можно также на данной прямой отложить отрезок, равный данному.

Решение задач на построение - это описание последовательности шагов с использованием основных простейших построений, которая приводит к построению искомой фигуры. Чтобы найти эту последовательность шагов, т.е. составить план решения задачи, обычно поступают так. Предполагают, что задача решена, делают примерный чертеж искомой фигуры, отмечают те отрезки и углы, которые известны из условия задачи, и стараются определить, к нахождению какой точки (прямой, угла) сводится решение задачи. После этого стремятся найти такую зависимость между данными и искомыми величинами, которая позволяет построить искомую точку (прямую, угол), и составляют план построения. Составление плана - самая важная часть задачи, ее называют анализом.

Выполнив анализ, наметив план, описывают само построение. Оно может содержать лишь основные построения и элементарные действия с циркулем и линейкой.

Далее требуется привести доказательство того, что построенная фигура удовлетворяет всем условиям задачи и, кроме того, проделать исследование, т.е. выяснить, всегда ли (при любых ли данных) описанное построение возможно, нет ли частных случаев, в которых построение упрощается или делается невозможным.

Таким образом, решение задачи на построение состоит из 4-х частей: анализ, построение, доказательство, исследование. Анализ опускается в простых задачах или в тех, решение которых уже известно.

1.Задача на бисекцию. С помощью циркуля и линейки разбить данный отрезок AB на две равные части или угол разделить пополам

2.Задача Аполлония о построении окружности, касающейся трех заданных окружностей. Если ни одна из заданных окружностей не лежит внутри другой, то эта задача имеет 8 существенно различных решений.

3.Задача Брахмагупты о построении вписанного четырехугольника по четырем его сторонам.

Неразрешимые задачи

Следующие три задачи на построение были поставлены ещё древними греками:

1.трисекция угла — разбить произвольный угол на три равные части;

2.удвоение куба — построить ребро куба вдвое большего по объёму, чем данный куб;

3.квадратура круга — построить квадрат, равный по площади данному кругу.

Лишь в XIX веке было строго доказано, что все эти три задачи неразрешимы при использовании только циркуля и линейки. Доказательство неразрешимости этих задач построения было достигнуто с помощью алгебраических методов, основанными на теории Галуа[1]. В частности, невозможность построения квадратуры круга следует из трансцендентности числа π.

Другая известная и неразрешимая с помощью циркуля и линейки задача — построение треугольника по трём заданным длинам биссектрис[2]. Эта задача остаётся неразрешимой даже при наличии инструмента, выполняющего трисекцию угла, например томагавка.[3]

Искусство построения геометрических фигур при помощи циркуля и линейки было в высокой степени развито в Древней Греции. Одна из труднейших задач на построение, которую уже тогда умели выполнять, - построение окружности, касающейся трех данных окружностей. Эта задача называется задачей Аполлония – по имени греческого геометра Аполлония из Перги (ок. 200 г. до н.э.).

Однако древним геометрам никак не удавалось выполнить некоторые построения, используя лишь циркуль и линейку, а построения, выполненные с помощью других инструментов, не считались геометрическими. К числу таких задач относятся так называемые три знаменитые классические задачи древности: квадратура круга, трисекция угла и удвоение куба, а именно построение квадрата, равновеликого данному кругу, деление произвольного угла на три равные части и построение стороны куба, объем которого вдвое больше объема заданного куба.

Эти три задачи привлекали внимание выдающихся математиков на протяжении столетий, и лишь в середине прошлого века была доказана их неразрешимость, т.е. невозможность указанных построений лишь с помощью циркуля и линейки. Эти результаты были получены средствами не геометрии, а алгебры, что еще раз подчеркнуло единство математики. Однако до сих пор еще встречаются люди, которые пытаются найти решения указанных задач при помощи циркуля и линейки.

Еще одной интереснейшей задачей на построение с помощью циркуля и линейки является задача построения правильного многоугольника с заданным числом сторон. Древние греки умели строить правильный треугольник, квадрат, правильный пятиугольник и пятнадцатиугольник , а также все многоугольники, которые получаются из них удвоением числа сторон, и только их.

Новый шаг в решении поставленной задачи был сделан лишь в 1801 г. немецким математиком К. Гауссом, который открыл способ построения правильного семнадцатиугольника при помощи циркуля и линейки и указал все значения , при которых возможно построение правильного -угольника указанными средствами. Этими многоугольниками оказались лишь многоугольники, у которых количество сторон является простым числом Ферма (т.е. простым числом вида ) (см. Ферма малая теорема) или произведением нескольких различных простых чисел Ферма, а также те, которые получаются из них путем удвоения числа сторон. Таким образом, с помощью циркуля и линейки оказалось невозможным построить правильный семиугольник, девяти-, одиннадцати-, тринадцатиугольник и т.д.

Теорема Морли . Одна из трех знаменитых задач древности задача о делении произвольного угла на три равные части. Лишь сравнительно недавно было доказано, что деление угла с помощью циркуля и линейки не всегда возможно. Видимо, этим объясняется то, что лишь в 1899 г. был открыт следующий удивительный факт: если в произвольном треугольнике разделить каждый угол на три равные части, то точки пересечения делящих их лучей (рис. 1) окажутся вершинами равностороннего треугольника. Эта теорема получила название теоремы Франка Морли, по имени американского математика, открывшего этот факт. Позже было замечено, что этим свойством обладают также и точки пересечения лучей, делящих на равные части внешние углы произвольного треугольника (рис. 2).

Задачи на построение

1.Разделить отрезок пополам.

2.Построить биссектрису угла.

3.Построить угол с вершиной в данной точке, с данной стороной угла, по указанную сторону от нее и равный данному.

4.Построить треугольник по трем сторонам.

5.Построить треугольник по двум сторонам и углу между ними.

6.Построить треугольник по стороне и двум углам, прилежащим к ней.

7.Построить прямоугольный треугольник по двум катетам, или по катету и гипотенузе, или по катету и острому углу, или по гипотенузе и острому углу.

8.Построить равнобедренный треугольник по основанию и радиусу описанной окружности.

9.Построить прямую, касательную к данной окружности и проходящую через данную точку вне этой окружности.

10.При выполнении графических работ приходится решать многие задачи на построение. Наиболее встречающиеся при этом задачи — деление отрезков прямой, углов и окружностей на равные части, построение различных фигур.

Деление отрезка прямой

Чтобы разделить заданный отрезок АВ на две равные части, точки его начала и конца принимают за центры, из которых проводят дуги радиусом, по величине превышающим половину отрезка АВ. Дуги проводят до взаимного пересечения, где получают точки С и D. Линия, соединяющая эти точки, разделит отрезок в точке К на две равные части (рис. а).

Чтобы разделить отрезок АВ на заданное количество равных участков п, под любым острым углом к АВ проводят вспомогательную прямую, на которой из общей заданной прямой точки откладывают п равных участков произвольной длины (рис. б). Из последней точки (на чертеже — шестой) проводят прямую до точки В и через точки 5, 4, 3, 2, 1 проводят прямые, параллельные отрезку 6В. Эти прямые и отсекут на отрезке АВ заданное число равных отрезков (в данном случае 6).

геометрические построения - Деление окружности

Чтобы разделить окружность на четыре равные части, проводят два взаимно перпендикулярных диаметра: на пересечении их с окружностью получаем точки, разделяющие окружность на четыре равные части (рис. а).

Чтобы разделить окружность на восемь равных частей, дуги, равные четвертой части окружности, делят пополам. Для этого из двух точек, ограничивающих четверть дуги, как из центров радиусов окружности выполняют засечки за ее пределами. Полученные точки соединяют с центром окружностей и на пересечении их с линией окружности получают точки, делящие четвертные участки пополам, т. е. получают восемь равных участков окружности (рис. б).

На двенадцать равных частей окружность делят следующим образом. Делят окружность на четыре части взаимно перпендикулярными диаметрами. Приняв точки пересечения диаметров с окружностью А, В, С, D за центры, величиной радиуса проводят четыре дуги до пересечения с окружностью. Полученные точки 1, 2, 3, 4, 5, 6, 7, 8 и точки А, В, С, D разделяют окружность на двенадцать равных частей (рис. в).

Пользуясь радиусом, нетрудно разделить окружность и на 3, 5, 6, 7 равных участков.

Актуальность выбранной темы объясняется тем, что как только на уроках математики начинают выполняться геометрические построения, сразу появляется интерес и улучшается математическое развитие. Задачи на построение вырабатывают и помогают лучше представить конкретную геометрическую фигуру и дополнительные элементы. Все это помогает развивать пространственное мышление и воображение. Также геометрические задачи на построение способны повысить уровень логического мышления, интуиции, внимания, целеустремленности, изобретательности, дисциплинированности и трудолюбия.

Проблема исследования состоит в следующем: рассмотрение различных методов решения геометрических задач на построение.

На самом деле, решая замечательные задачи по геометрии, в числе которых упражнения на построение в главной роли, школьники получают много необходимых качеств:

1) умение представлять различные геометрические образы;

2) в уме решать операции над вымышленными геометрическими построениями.

Задачи на построение помогают логически думать.

На самом деле, из чего состоит путь выполнения геометрической задачи на построение? У ученика возникает одна цель: начертить необходимое в задаче построение. Для того, чтобы решить эту цель ему необходимо будет вникнуть в условие задачи и вспомнить нужные темы из геометрии. Только самые легкие задачи получится выполнить без особых раздумий. Во многих случаях, прежде чем построить окончательный рисунок, необходимо выполнить пару вспомогательных , которые являются логическими умозаключениями.

Самый первый вспомогательный рисунок строится на основе условия задачи и на различных сведениях, не зная которых нельзя решить данную задачу. Если необходимо построить второй вспомогательный рисунок, то первое вносится в число данных. Выполняя один за другим такие действия, ученик находит окончательное правильное построение. Но не всегда вспомогательные построения могут быть верными и приводить к нужной цели. В таких случаях их просто отбрасывают.

Когда ученик находит требуемое построение, он должен логически доказать верность своих действий, основываясь на учебный материал. А так же выявить, всегда ли данная задача имеет решение.

История развития геометрии ведет свое начало с древних времен. Людям необходимо было как-то измерять земельные участки. Отсюда и пошло название геометрия: geo - земля, metria – мера (землемерие).

Позже геометрия вылилась в отдельную самостоятельную науку, выйдя за пределы первоначального определения.

В своем развитии как науки, геометрия прошла несколько периодов.

Зарождение геометрии датируется приблизительно 5 веком до нашей эры и ведет свое начало с Древнего Египта, Вавилона и Греции.

Частые затопления земельных участков, расположенных на берегу Нила, требовали постоянного восстановления границ после спада воды. Это вынудило египтян заняться измерениями земли. Позже, с развитием торговли, потребовалось необходимость в измерении емкости сосудов. Постройка пирамид для захоронения фараонов также требовала знаний пространственных форм.

В 7 в.до н.э. знания египтян были позаимствованы греками. И именно благодаря греческим ученым, систематизировавшим сведения о геометрии, она вылилась в отдельную науку.

Однако в Евклидовых трудах отсутствовали данные об измерениях объемов и поверхности.

Дальнейший толчок к развитию геометрии было дано Архимедом, вычислившем число Пи, нашедшим способы вычислять поверхность шара. Кроме того, Архимедом была выведена формула для нахождения площади треугольника через три его стороны. Это дало возможность решать геометрические задачи, имеющие значение в мореплавании и строительном деле.

Первая половина 17 века ознаменовалась введением Декартом системы координат. Это послужило началом для перехода геометрии на более качественную ступень развития, объединив ее с алгеброй.

В процессе дальнейшей эволюции геометрической науки возникло два новых направления: дифференциальная геометрия и проективная.

Основателями дифференциальной геометрии считаются Эйлер и Монжа. В развитие проективной геометрии внесли большой вклад французские математики Ж.Дезарг и Б.Паскаль. Суть проективной геометрии в том, что она изучает свойства и отношения, остающиеся неизменными при проецировании одной плоскости на другую.

Евклидова система не решала многие астрономические вопросы. Труды же Лобачевского дали толчок не только к развитию геометрии, но и высшей математики и астрономии.

История развития геометрической науки на этом не закончена. Расширение круга фигур, их свойств, изменение понятий об объектах требует постоянного развития науки.

Задачи, для решения которых в древности необходимо было бы затратить много времени и сил, сейчас решаются быстро и легко.

Популярные сегодня темы

Кувшинка белая плавает на поверхности, но после цветения затягивает цветок под воду, где развивается плод. Когда семена созревают возвращается на поверхность.

Фотосинтез – это процесс, который представляет из себя трансформацию лучистой энергии солнца в химическую энергию. Таким образом природа приспособилась к использованию солнечной энергии для т

Паукообразные не имеют никакого отношения к насекомым. Они представляют отдельную группу животного мира. Главное их отличие – количество ножек – их 8. К этой категории относятся: скорпионы, к

Окружающая среда - то место, где обитает человек и разные виды животных. Соответственно, этих сред очень много на Земле.

Рим – великая империя, подарившая миру множество памятников культуры. Человек, который воочию видит всю архитектуру, погружается в историю. Это великолепное чувство.

Планета Сатурн является 6 по счету от Солнца и представляет собой огромный газовый гигант, который обрамляется тысячей светящихся колец. Таким образом Сатурн представляет собой в действительн

Цель – показать необходимость изучения этой науки (геометрии), которая дает возможность понять, а также рассмотреть значение геометрических законов и закономерностей, их практическое применение при проектировании и постройке сооружений.

Фигура – это произвольное множество точек на плоскости. Точка, прямая, отрезок, луч, треугольник, круг, квадрат и так далее – всё это примеры геометрических фигур.
Основными геометрическими фигурами на плоскости являются точка и прямая. Этим фигурам в геометрии не даётся определений. Неопределяемыми геометрическими фигурами на плоскости являются точка и прямая. Точки принято обозначать прописными латинскими буквами: А, В, С, D …. Прямые обозначаются строчными латинскими буквами: а, b, с, d ….

1.Основные геометрические понятия.

Основные геометрические понятия возникли еще в доисторические времена. Наблюдая за формами растений и животных, гор и извилинами рек, за особенностями ландшафта и далекими планетами, человек заимствовал у природы ее правильные формы, размеры и свойства. Материальные потребности побуждали человека строить жилища, изготавливать орудия труда и охоты, лепить из глины посуду и прочее. Все это постепенно способствовало тому, что человек пришел к осознанию основных геометрических понятий. Одним из первых достижений абстрактного мышления древнего человека стало понимание прямой линии.

Прямая не проходит через точку, если точка не принадлежит ей.

Пряма́я — одно из фундаментальных понятий геометрии.
При систематическом изложении геометрии прямая линия обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии (евклидовой).Если основой построения геометрии служит понятие расстояния между двумя точками пространства, то прямую линию можно определить как линию, путь вдоль которой равен расстоянию между двумя точками. Аналитически прямая задаётся уравнением (в трёхмерном пространстве — системой уравнений) первой степени.

К основным свойствам прямой относятся:

Черед две различные точки проходит одна единственная прямая. Следовательно две прямые не могут иметь более одной общей точки.

Две разные прямые, имеющие общую точку, пересекаются в ней. В связи с тем, что две точки определяют прямую, проходящую через них, прямую обозначают сочетанием букв, к примеру, прямая АВ, прямая PQ.

Точка М, лежащая на прямой а, разбивает её на две части. Каждая из которых называется полупрямой или лучом. Точка М служит началом каждого их этих лучей. Две точки М и N разбивают прямую на три части: два луча МР и NQ и отрезок MN.

Прямая разбивает плоскость на 2 части. Часть плоскости лежащая по одну сторону от этой прямой, называется полуплоскостью.

Если прямые не имеют общих точек, говорят, что они параллельны.

Если две прямые имеют одну общую точку, говорят, что они пересекаются в этой точке.

Две прямые в трёхмерном евклидовом пространстве скрещиваются, если не существует плоскости, их содержащей. Иначе говоря, две прямые в пространстве, не имеющие общих точек, и не являющиеся параллельными.

2. Параллелограмм.

Параллелограмм (др.-греч. παραλληλόγραμμον от παράλληλος — параллельный и γραμμή — черта, линия) — это четырёхугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных прямых.

Частными случаями параллелограмма являются прямоугольник, квадрат и ромб.

Признаки параллелограмма:
Четырёхугольник является параллелограммом, если выполняется одно из следующих условий:
1. Если в четырёхугольнике противоположные стороны попарно равны, то четырёхугольник - параллелограмм
2. Если в четырёхугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник - параллелограмм
3. Если в четырёхугольнике две стороны равны и параллельны, то этот четырёхугольник - параллелограмм

Параллелограмм, у которого все углы прямые, называется прямоугольником.
Теорема. Если в параллелограмме диагонали равны, то он является прямоугольником.
Параллелограмм, у которого все стороны равны, называется ромбом.
Теорема. Если в параллелограмме диагонали перпендикулярны, то он является ромбом.

Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции. Расстояние между основаниями называется высотой трапеции.

Средняя линия трапеции параллельна основаниям и равна их полусумме.

Отрезок, соединяющий середины диагоналей, равен полуразности оснований.

В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.

Трапеция, у которой боковые стороны равны, называется равнобокой или равнобедренной.
Свойства равнобедренной трапеции.

Прямая, проходящая через середины оснований, перпендикулярна основаниям и является осью симметрии трапеции.

В равнобедренной трапеции углы при любом основании равны.

В равнобедренной трапеции длины диагоналей равны.

Если трапецию можно вписать в окружность, то она равнобедренная.

Около равнобедренной трапеции можно описать окружность.

Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.

Трапеция, имеющая прямые углы при боковой стороне, называется прямоугольной.

4.Окружность.

Окружность – это плоская замкнутая линия, все точки которой находятся на одинаковом расстоянии от некоторой точки (точки О), которая называется центром окружности.
(Окружность — геометрическая фигура, состоящая из всех точек, расположенных на заданном расстоянии от данной точки.)
Круг – это часть плоскости, ограниченная окружностью. Точка О также называется центром круга. Расстояние от точки окружности до её центра, а также отрезок, соединяющий центр окружности с её точкой, называется радиусом окружности/круга.

Хорда - греческое - струна, стягивающая что-то
Диаметр - "измерение через"
Углы могут встречаться во все более возрастающем количестве, приобретать, соответственно, все больший разворот – пока не исчезнут окончательно и плоскость не станет кругом. Это очень простой и одновременно очень сложный случай, о котором мне хотелось бы поговорить подробно. Здесь необходимо отметить, что как простота, так и сложность обусловлены отсутствием углов. Круг прост, поскольку давление его границ, в сравнении с прямоугольными формами, нивелировано – различия здесь не так велики. Он сложен, поскольку верх неощутимо перетекает в левое и правое, а левое и правое – в низ.

В Древней Греции круг и окружность считались венцом совершенства. Действительно, в каждой своей точке окружность устроена одинаковым образом, что позволяет ей двигаться самой по себе. Это свойство окружности сделало возможным возникновение колеса, поскольку ось и втулка колеса должны все время быть в соприкосновении. В школе изучается много полезных свойств окружности. Одной из самых красивых теорем является следующая: проведем через заданную точку прямую, пересекающую заданную окружность, тогда произведение расстояний от этой точки до точек пересечения окружности с прямой не зависит от того, как именно была проведена прямая. Этой теореме около двух тысяч лет. Эта фигура получается, если провести дуги окружностей с центрами в вершинах равностороннего треугольника, соединяющие две другие вершины. Если провести к этой фигуре две параллельные касательные, то расстояние между ними будет равно длине стороны исходного равностороннего треугольника, так что такие катки ничем не хуже круглых. В дальнейшем были придуманы и другие фигуры, способные выполнять роль катков.

У каждого треугольника имеется, и притом единственная, окружность девяти точек. Это окружность, проходящая через следующие три тройки точек, положение которых определено для треугольника : основания его высот D1 D2 и D3, основания его медиан D4, D5 и D6 середины D7, D8 и D9 отрезков прямых от точки пересечения его высот Н до его вершин. Эта окружность, найденная в XVIII в. великим ученым Л. Эйлером (поэтому ее часто также называют окружностью Эйлера), была заново открыта в следующем столетии учителем провинциальной гимназии в Германии. Звали этого учителя Карл Фейербах (он был родным братом известного философа Людвига Фейербаха). Дополнительно К. Фейербах выяснил, что окружность девяти точек имеет еще четыре точки, тесно связанные с геометрией любого данного треугольника. Это -точки ее касания с четырьмя окружностями специального вида. Одна из этих окружностей вписанная, остальные три - вневписанные. Они вписаны в углы треугольника и касаются внешним образом его сторон. Точки касания этих окружностей с окружностью девяти точек D10, D11, D12 и D13 называются точками Фейербаха. Таким образом, окружность девяти точек является в действительности окружностью тринадцати точек. Окружность эту очень легко построить, если знать два ее свойства. Во-первых, центр окружности девяти точек лежит в середине отрезка, соединяющего центр описанной около треугольника окружности с точкой Н- его ортоцентром (точка пересечения его высот). Во-вторых, ее радиус для данного треугольника равен половине радиуса описанной около него окружности.

5.Треугольник.

Треуго́льник (в евклидовом пространстве) — это геометрическая фигура, образованная тремя отрезками, которые соединяют три не лежащие на одной прямой точки. Три точки, образующие треугольник, называются вершинами треугольника, а отрезки — сторонами треугольника.
Стороны треугольника образуют в вершинах треугольника три угла. Другими словами, треугольник — это многоугольник, у которого имеется ровно три угла.

Вершины — три точки А, В и С. Стороны — отрезки АВ, ВС и СА.
Углы — ∟ ВАС, ∟ СВА и ∟ АСВ.
Периметр треугольника — сумма длин трех сторон треугольника.

Медиана треугольника (m)— отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Биссектриса треугольника (b) — отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны. Высота треугольника (h)— перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону.

В любом треугольнике медианы пересекаются в одной точке, биссектрисы пересекаются в одной точке, высоты или их продолжения также пересекаются в одной точке.

Теорема. Сумма углов треугольника 180°. Каждая сторона треугольника меньше суммы двух других сторон.

1) против большей стороны лежит больший угол.

2) против большего угла лежит большая сторона.

В прямоугольном треугольнике гипотенуза больше катета

Классификация треугольников по углам. В треугольнике может быть только один тупой угол. В треугольнике может быть только один прямой угол. По сторонам.
Треугольник называется равнобедренным, если две его стороны равны.
Равные стороны называются боковыми сторонами, а третья сторона — основанием равнобедренного треугольника.

5.1. Теоремы треугольника.

В равнобедренном треугольнике углы при основании равны.
Теорема

В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.

Равносторонний треугольник — все стороны и углы равны.

Если два треугольника равны, то элементы (т. е. стороны и углы) одного треугольника соответственно равны элементам другого треугольника.
В равных треугольниках против соответственно равных сторон лежат равные углы.

5.2.Признаки треугольника.

ПЕРВЫЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВ
Теорема:
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

ВТОРОЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВ
Теорема. Если сторона и два прилежащих угла одного треугольника соответственно равны стороне и двум прилежащим углам другого треугольника, то такие треугольники равны.

ТРЕТИЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВ
Теорема. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

5.3.Прямоугольный треугольник.

СВОЙСТВА ПРЯМОУГОЛЬНЫХ ТРЕУГОЛЬНИКОВ

• Сумма двух острых углов прямоугольного треугольника равна 90°.
• Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы.
• Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30°.

ПРИЗНАКИ РАВЕНСТВА ПРЯМОУГОЛЬНЫХ ТРЕУГОЛЬНИКОВ
Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого, то такие треугольники равны.

Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны.

Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны.

Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету.

5.4. История изучения треугольника.

6.Многоугольник.

Многоугольник — фигура, составленная из отрезков так, что смежные отрезки не лежат на одной прямой, а несмежные отрезки не имеют общих точек.
Точки А, В, С, D, Е… — вершины многоугольника. Отрезки АВ, ВС, CD, DE, ЕА,… - стороны многоугольника.
Периметр многоугольника (гречечкое пери - вокруг, около) — сумма длин всех сторон.
Многоугольник с n вершинами называется n-угольником; он имеет n сторон.
Две вершины многоугольника, принадлежащие одной стороне, называются соседними.
Диагональ многоугольника (греческое dia - через, gonia - угол, т.е. проходящая через углы) — отрезок, соединяющий любые две несоседние вершины.
Любой многоугольник разделяет плоскость на две части, одна из которых называется внутренней, а другая — внешней областью многоугольника. Фигуру, состоящую из сторон многоугольника и его внутренней области, также называют многоугольником.

Многоугольник называется выпуклым:

1) если он лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины

2) если вместе с любыми своими 2 точками он содержит и соединяющий их отрезок.

Сумма углов выпуклого п-угольника равна (n- 2) 180°.

Многоугольником может называться замкнутая ломаная с самопресечениями и правильные звёздчатые многоугольники.

Площадь многоугольника — это величина той части плоскости, которую занимает многоугольник.

1) равные многоугольники имеют равные площади;

2) если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников;
3) площадь квадрата равна квадрату его стороны.

7. Многранники. Виды многранников

В современном мире нас окружает множество построек состоящих из сложных геометрических фигур, большинство из которых являются многогранниками. Примеров тому очень много, достаточно посмотреть по сторонам и мы заметим что здания, в которых мы живём, магазины, в которые ходим, школы и детские сады и т.д. представлены в виде многогранников.

Призма – это многогранник, две грани которой ABCDE и abcde ( основания призмы ) – равные многоугольники с соответственно параллельными сторонами, а остальные грани ( AabB, BbcC и т.д. ) - параллелограммы, плоскости которых параллельны прямой ( Aa, или Bb, или Cc и т.д. По основанию:

-Небоскрёб Flat Iron (Утюг) на пересечении Бродвея и Пятого Авеню. Построен в 1902 году. 21 этаж, 87 метров

-Пентагон — здание Министерства обороны США в форме пятиугольника. Находится в штате Вирджиния недалеко от Вашингтона.

-Наклонная призма – боковое ребро наклонено к основанию под углом отличны от 90є.

Прямая призма – боковое ребро расположено перпендикулярно к основанию.

7.2. Параллелепипед

Параллелепипед - призма, в основании которой находится параллелограмм.

Наклонный, Прямой, Прямоугольный – это прямой параллелепипед,

в основании которого прямоугольник.

Куб – это прямой параллелепипед,

все грани которого квадраты

7.3. Пирамида

Пирамида – это многогранник, одна из граней которого – произвольный n-угольник, а остальные “n” граней – треугольники, имеющие общую вершину.

-Университетский волейбольно-баскетбольный стадион в Калифорнии

В основании - Квадрат

-Торговый центр в Турции

Цилиндр – это тело, ограниченное частью замкнутой цилиндрической поверхности и частью двух плоскостей, параллельных между собой

Водонапорная башня в Минске, Нефтехранилища, Небоскреб в США

Конус - это геометрическое тело, ограниченное частью конической поверхности, расположенной по одну сторону от вершины и частью пересекающей её плоскости.

Как самостоятельные сооружения конусы в строительстве не используются. Практически всегда они составляют какую-то часть здания, например крыши и архитектурные украшающие детали.

Также в строительстве используют конические сваи.

7.6. Сфера и шар.

Сфера – это множество всех точек пространства, находящихся на положительном расстоянии R от данной точки О, называемой центром сферы.

Шар – это множество всех точек пространства, расстояние которых от данной точки не превосходит заданного положительного числа R. Шар получается при вращении полукруга относительно диаметра.

Шаровой слой – это часть шара, заключенная между двумя параллельными плоскостями.

Шаровой сегмент – это часть шара, отсекаемая от него плоскостью.

ТРК Вояж, г. Санкт-Петербург, Здание в Париже (Франция)

Здание Национального Конгресса в США

Итак, при постройке, как современных зданий, так и зданий прошлых веков необходимы знания геометрии. Архитектурное формообразование с помощью геометрических построений сохраняется во всех случаях. Эта проблема стояла перед архитекторами прошлых веков, не исчезла она и сегодня.

7.7. Двойной квадрат

Два квадрата, сложенные вместе, образуют двойной квадрат. Сложив два двойных квадрата, получим квадрат, повторяющий своими очертаниями исходный квадрат. Это простое аддитивное свойство квадрата широко использовалось в архитектуре эпохи Возрождения.

7.8. Восьмиугольные звезды.

Использование восьмиугольных звезд в архитектурных конструкциях не вызывает никаких сомнений. Автором этого проекта является Леонардо да Винчи.

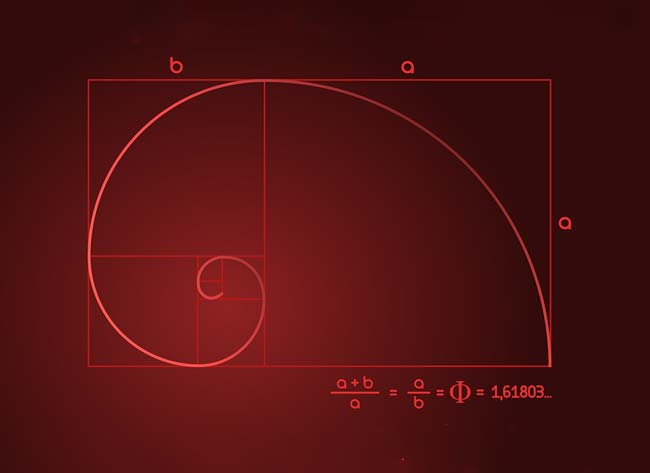
Золото́е сече́ние (золотая пропорция, деление в крайнем и среднем отношении) — деление непрерывной величины на две части в таком отношении, при котором меньшая часть так относится к большей, как большая ко всей величине.

Исследовательская работа ученика 7 класса по теме: "Геометрия вокруг нас". Цель данной работы: показать практическое применение геометрии.

Вложение	Размер
tvorcheskaya_rabota_geometriya_vokrug_nas.docx	42.26 КБ

Предварительный просмотр:

Муниципальное автономное образовательное учреждение

Автор: Зырянов Кирилл, 7 класс

Научный руководитель: Пахомова

2.2 Геометрия в жизни людей…….…………………………………….6

2.3. Геометрия в природе………………………………………………. 7

2.4. Практическое применение геометрии …..…………………………8

Заключение………………………………………………………..…. 11
Список использованных источников, литературы…………………12

«Геометрия является самым могущественным средством

для изощрения наших умственных способностей и дает

Проблема исследования: как можно применить на практике знания, полученные на уроках геометрии, есть ли связь между геометрией и другими учебными предметами.

Объект исследования: геометрия.

Предмет исследования: практическое применение геометрии.

Гипотеза исследования: геометрия необходима не только как школьная дисциплина, но и важна в повседневной жизни.

Цель исследования: Роль геометрии в жизни человека.

Исследовать и показать как можно больше способов практического применения геометрии.
Научиться их применять в повседневной жизни.
Показать одноклассникам практическое применение геометрии.

- поисковый метод с использованием научной и учебной литературы, интернета;

- исследовательский метод при решении практических задач по геометрии.

II. Основная часть.

2.1. Немного истории.

2.2. Геометрия в жизни человека.

Геометрические знания связаны со многими современными специальностями. Например, архитектор, который перед тем как построить жилое здание, придумывает основную концепцию здания, его облик, проектируют будущую постройку на чертежах в уменьшенном масштабе. Задача архитектора — спроектировать сооружение, максимально отвечающее потребностям заказчика.

Оказывается геометрия тесно связана с искусством, т.к. одним из ранних этапов развития искусства Древней Греции (IX-VIII вв. до н. э.) является техника геометрической живописи. Это проявляется в росписи утвари. Геометрическому стилю присуще многообразие и четкость узоров , их строгость подчёркивает построение конструктивного предмета . Орнамент располагается полосами и получается из ломанных линий, крестов, окружностей. В более поздний период развития Древней Греции появляется изображение образа человека из геометрических фигур. А в начале XX века появилось авангардное направление в живописи –кубизм . В этом направлении используется множество геометрических фигур.

Геометрия непосредственно связана с модой. Множество геометрических фигур можно увидеть в основных частях костюма. Построение геометрических фигур необходимо не только на уроках геометрии, но и в конструировании одежды.

Самым неожиданным для меня явилось то, что геометрия нужна в психологии. В психологии есть система, с помощью которой можно определить характер человека, его способности, манеру общения. Данная система называется- психогеометрия. В основе психогеометрии лежит пять типов личности, которым соответствуют геометрические фигуры квадрат , треугольник , прямоугольник , круг и загзаг . Человек выбирает ту, с которой ассоциируете себя. Оставшиеся фигуры пронумерует в порядке убывания предпочтения. Выбранная фигура и определяет основные черты характера. А последняя фигура, в вашем пронумерованном списке, может обозначать персоны, контакты с которой будут наиболее затруднительными для тестируемого.

2.3 Геометрия в природе.

Если посмотреть вокруг, то можно увидеть что большая часть тел в природе имеют шарообразную форму. Примером могут служить ягоды, фрукты, цветы и даже некоторые животные имеют форму шара. Например, рыба-еж, ядовитая рыба – фугу. Икра всех рыб представляет форму шара. Многие бактерии - шарообразны. Если взять любое насекомое, то его как будто сконструировали по чертежу. Глаза стрекозы, занимающие большую часть её головы, состоят из более 30 000 мелких глазков (фасеток). Что интересно, каждый миниатюрный глаз способен работать независимо от других. Верхняя часть фасеток предназначена для распознавания формы предмета, а нижняя – его цвета. Яйца у птиц имеют шаровидную или продолговатую форму. Многие животные спят, свернувшись клубком, т.к. поверхность тела уменьшается, и тепло лучше сохраняется. Итак, природа часто использует круг и его объемный эквивалент – сферу. Небесные тела большой массы, такие как звезды, планеты и спутники тоже сферической формы. Сила притяжения толкает каждый атом к центру тела. Со временем оно приобретает сферическую форму, потому что именно в ней достигается максимальная концентрация массы при минимальной площади внешней поверхности.

Конечно не только шарообразная форма присутствует в природе. Например, пчелы строят соты в форме шестиугольников, что позволяет им хранить максимально возможное количество меда, используя минимальное количество воска.

Есть около 5000 типов пауков, и все они создают почти идеальное круговое полотно с радиальными поддерживающими нитями почти на равном расстоянии и спиральной тканью для ловли добычи. Ученые не уверены, почему пауки так любят геометрию, так как испытания показали, что круглое полотно не заманит еду лучше, чем полотно неправильной формы. Ученые предполагают, что радиальная симметрия равномерно распределяет силу удара, когда жертва попадает в сети, в результате чего получается меньше разрывов.

Один из примеров симметрии являются круги на полях, которые отличаются сложностью дизайна и невероятной симметрией, даже после того, как создатели кругов признались и продемонстрировали свое мастерство, многие люди до сих пор верят, что это сделали космические пришельцы.

Даже такие крошечные образования, как снежинки, регулируются законами симметрии, так как большинство снежинок имеет шестигранную симметрию. Это происходит в частности из-за того, как молекулы воды выстраиваются, когда затвердевают (кристаллизуются). Молекулы воды приобретают твердое состояние, образуя слабые водородные связи, они выравниваются в упорядоченном расположении, которое уравновешивает силы притяжения и отталкивания, формируя гексагональную форму снежинки. Но при этом каждая снежинка симметрична, но ни одна снежинка не похожа на другую. Это происходит потому, что падая с неба, каждая снежинка испытывает уникальные атмосферные условия, которые заставляют её кристаллы располагаться определенным образом.

2.4 Практическое применение геометрии.

Сделав вывод о том ,что природа всегда останавливает выбор на самых стабильных формах, минимально расходующих энергию, я подумал о том, чем мне может помочь геометрия в жизни. Не зря ли я трачу время на изучение данного предмета? Возможно они мне пригодятся только для того, чтобы измерить расстояние от точки до точки, вычислить площадь или объём предмета и только? Нет, конечно. Законы геометрии применимы буквально на каждом шагу. Просто нужно знать, как ими воспользоваться.

Перед нами стеклянные чайники четырёх моделей одинаковой вместимости (рис. 2). В каком чайнике заваренный чай останется тёплым дольше?

Решение. Из курса физики известно, что время охлаждения пропорционально площади поверхности тела. Значит, чем меньше поверхность чайника, тем дольше остывает чай. Самая маленькая площадь поверхности у четвёртого чайника, так как его форма близка к сфере (S = d 2 ).

Задача №2. Часто в рецептуре того или иного блюда требуется взять четверть (или половину) стакана жидкости, муки либо какого-либо другого продукта. Как отмерить такой объём с наибольшей точностью, не прибегая к дополнительным измерительным средствам?

Решение. Воспользуемся стаканом цилиндрической формы — это важно для точности измерений. Чтобы отмерить четверть стакана жидкости, надо из наполненного стакана вылить столько, чтобы оставшаяся в нём жидкость закрыла половину дна . Она займёт примерно четверть объёма стакана-цилиндра. Аналогично поступаем, если надо отмерить половину стакана. Наклоняем стакан так, чтобы оставшаяся в нём жидкость закрыла всё дно.

Задача№3. Прямоугольная калитка со временем расшатывается и становится похожей на параллело-грамм. Этого можно избежать, прибив к ней ещё одну планку. Только надо знать, как это сделать.

Решение. Выбор такого положения планки, как показано на рис. 10, справа, основан на свойстве жёсткости треугольника. Оно гласит: существует единственный треугольник с заданными длинами сторон. Планка и есть гипотенуза такого треугольника.

Задача №4. На какой табурет можно сесть без риска оказаться на полу, на тот у которого ножки и сиденье образуют треугольник или квадрат?

Решение. Безопасный табурет тот, у которого сиденье и ножки образуют треугольник(более устойчив).

Задача №6. Как без всяких измерений найти середину негнущегося прута, доски или металлического стержня?

Решение. Можно отмерить размеры стержня на шнуре, затем сложить его пополам и отложить полученную длину. А можно воспользоваться геометрическим построением середины отрезка с помощью циркуля и линейки, если, конечно, размеры позволяют это сделать. Ещё более рациональное решение даёт физика. Середину однородного стержня легко найти, используя понятие центра тяжести.

Задача №7. Один из вопросов, который меня всегда мучил – почему крышки люков круглые?

Оказывается есть еще ответ, который опирается на знания формул площадей круга и квадрата. Люки делают круглыми с целью снижения себестоимости их производства. Это обусловливается спецификой оборудования: для того, чтобы изготовить круглую крышку, необходимо меньше материала. Стандартные нормы ширины люка – 600 мм, для круга это будет диаметр, а для квадрата – сторона, поэтому площадь квадратного люка будет равна 0,36 квадратных метров, а круглого – на 30 % меньше.

Еще одна практическая сторона: крышка люка круглая, поскольку ее удобно переносить. В большинстве случаев крышки люков делают из рашпера (серого чугуна), который получают путем переплавки различного металлолома. Вес одной крышки варьирует от 50 до 110 кг. Одному человеку перенести крышку люка с одного места на другое довольно тяжело, а благодаря круглой форме его можно перекатить.

Не квадратные, а именно люки круглой формы удобно монтировать и демонтировать, поскольку точки концентрации нагрузки идут по всей окружности крышки, в то время как у люков квадратной или прямоугольной формы такими точками будут только углы. Именно поэтому горлышки и, соответственно, крышки к банкам изготавливают круглыми.

Выдвинутая гипотеза о том, что геометрия необходима не только как школьная дисциплина, но и важна в повседневной жизни – подтвердилась.

Читайте также: