Реферат на тему тетраэдр
Обновлено: 02.07.2024
У любого тетраэдра 4 вершины, 6 рёбер, 4 грани, 4 трёхгранных угла, 6 двугранных углов, 12 плоских углов. Если все 6 рёбер равны, то равными будут и грани, и трёхгранные углы, и плоские; в этом случае тетраэдр - правильный. Из равенства всех 4 граней, однако, ещё не следует правильность тетраэдра; тетраэдр, у которого все грани равны, называется равногранным. Чтобы представить себе равногранный тетраэдр, отличный от правильного, возьмём произвольный остроугольный треугольник из бумаги и будем сгибать его по средним линиям. Тогда три вершины сойдутся в одну точку, а половинки сторон сомкнутся, образуя боковые рёбра тетраэдра (рис. 2).
Перечислим теперь свойства тетраэдра, каждое из которых является необходимым и достаточным условием равногранности, включая определение:
(1) Скрещивающиеся рёбра попарно равны (2) Трёхгранные углы равны.
(3) Противолежащие двугранные углы равны.
(4) Два плоских угла, опирающиеся на одно ребро, равны.
(5) Сумма плоских углов при каждой вершине равна 180.
(6) Развёртка тетраэдра - треугольник или параллелограмм
(7) Описанный параллелепипед - прямоугольный.
(8) Тетраэдр имеет три оси симметрии.
(9) Общие перпендикуляры скрещивающихся рёбер попарно перпендикулярны.
(10) Средние линии попарно перпендикулярны.
(11) Периметры граней равны.
(12) Площади граней равны.
(13) Высоты (тетраэдра) равны. 19=>18
(14) Отрезки, соединяющие вершины с центром тяжести пртивоположных граней, равны.
(15) Радиусы описанных около граней окружностей равны.
(16) Центр тяжести (тетраэдра) совпадает с центром описанной сферы.
(17) Центр тяжести (тетраэдра) совпадает с центром вписанной сферы.
(18) Центр вписанной сферы совпадает с центром описанной.
(19) Вписанная сфера касается граней в центрах описанных около них окружностей.
(20) Сумма внешних единичных векторов, перпендикулярных к граням, равна 0 (рис. 4).
(21) Сумма косинусов всех двугранных углов равна 2.
Все перечисленные условия являются одновременно и свойствами и признаками равногранного тетраэдра. Чтобы вывести равногранность из какого-нибудь условия, надо выстроить целую цепочку промежуточных условий, в которой каждое прямое следствие предыдущего.
Проще всего устанавливается, что (0) (1) (2) (3) (4).
Все грани тетраэдра АВСD равны по условию. Рассмотрим треугольники АDВ и DАС: АD общая, тогда АВ равна либо DС (если так, то из равенства треугольников АDВ и DАС следует АС=DВ; а из равенства треугольников АDВ и СВD следует АD=ВС, т.е. скрещивающиеся рёбра попарно равны), либо АС (если так, то из равенства треугольников АDВ и DАС следует DВ=DС, т.е. треугольник равнобедренный, а остальные нет, т.е. противоречие)
Из (1) следует, что треугольники АВD, СDВ, ВАС (рис.1) равны (доказано выше). Тогда равны и соответствующие углы треугольников, т.е. трёхгранные углы ВАСD, АВСD, САВD, DАВС равны, т.к. любой трёхгранный угол однозначно определяется своими тремя плоскими углами.
Т.к. трёхгранный угол однозначно определяется своими тремя плоскими углами, то сдедующие доказательства будут аналогичны предудущему.
Дальше можно рассуждать по следующей схеме: (4)=>(5)=>(6)=>(1) (откуда уже следует равносильность первых шести условий).
- Из условия следует, что углы ADB=ACB, ADC=ABC, BDC=BAC. Тогда треугольники ABC, ADC, ADB, BCD подобны, но треугольники ADB и DAC имеют общую сторону, т.е. они равны, аналогично равны екжду собой и остальные треугольники, т.е. тетраэдр равногранный.
- Разрежем тетраэдр АВСD по рёбрам АВ, АС, АD и рассмотрим развёртку А1ВА2DА3С (рис. => ), тогда в точках В, С и D приложены по три угла, сумма которых 180°, поэтому углы А1ВА2, А2ОА3, А3СА1 развернутые; значит, А1А2А3 треугольник, содержащий точки В, С, D и являющийся разверткой тетраэдра АВСD, Для остальных разверток рассуждение аналогично.
- Посмотрев на рисунок можно увидеть, что на развёртке (например треугольник) скрещивающиеся рёбра являются противоположными сторонами параллелограмма, т.е. они равны.
Наш следующий шаг - доказательство равносильности (1) (7).
В самом деле, поскольку скрещивающиеся ребра тетраэдра диагонали граней описанного параллелепипеда, из попарного равенства ребер следует, что грани описанного параллелепипеда прямоугольники и наоборот.
Теперь мы предлагаем рассуждать по схеме (7)=>(8)=>(9)=>(10)=>(7).
- Взглянув на (рис. =>), вы легко установите, что осями симметрии являются прямые, соединяющие центры симметрии противоположных граней описанного (прямоугольного) параллелепипеда, или, что здесь то же самое, общими перпендикулярами скрещивающихся рёбер.
- Общими перпендикулярами скрещивающихся рёбер являются отрезки соединяющие середины противоположных граней описанного параллелограмма (прямоугольного) (рис. ^), а это значит, что эти отрезки попарно перпендикулярны (т.к. каждый из отрезков перпендикулярен граням, которые он соединяет).
- Отрезки, соединяющие середины скрещивающихся рёбер перпендикулярны, но это и есть средние линии.
Следующая цепочка рассуждений (0)=>(11),(12),(13),(14),(15). Мы докажем, что (11)=>(1), (12)=>(3), (13)=>(12), (14)=>(1), (4)=>(15); тем самым будет установлена равносильность первых 15 свойств.
- Запишем условие (11) в виде a2+b2+c2 (1) =a2+b1+c1 (2) =b2+a1+c1 (3) =c2+a1+b1 (4), где a1b1c1 длины рёбер тетраэдра, исходящих из одной вершины, a2b2c2 длины соответственно скрещивающихся с ними рёбер. (1)-(2)=(3)-(4) или b2+c2-b1-c1=b2+c1-c2-b1, т.е. 2с2=2с1 или по-другому с2=с1, рассуждая аналогично для a1,a2,b1,b2, получаем a1=a2, b1=b2, c1=c2, а это и есть запись условия (1).
- Для этого утверждения предварительно заметим, что S4=S1c14+S2c24+S3c34 (**), где Si - площади i-й грани, а сij косинус двугранного угла между i-й и j-й гранью. Соотношение (**) сразу следует из теоремы о площади проекции, если спроектировать все грани тетраэдра на четвёртую грань. Написав ещё три таких соотношения (для трёх других граней) и воспользовавшись условием (12), приходим к системе с14+с24+с34=с13+с23+с34=с12+с23+с24=с12+с13+с14, которая решается точно так же как система из предыдущего утверждения. Получим с14=с23, с24=с14, с34=с12 , откуда следует равенство соответствующих углов, т.е. (3).
- Утверждение очевидно следует из формулы для объёма тетраэдра V=Sh/3: S1h1/3=S2h2/3=S3h3=S4h4/3 S1=S2=S3=S4 по условию => h1=h2=h3=h4.
-
Обозначим через Оi центр тяжести i-й грани и выразим |DO4| через стороны /DA/=/a/, /DB/=/b/, /DC/=/c/ (рис. =>). /DO4/ = =/DA/ + + /AO4/ = /DA/ + 2/3*/AE/ = /DA/ + 2/3*1/2*(/AB/ + /AC/) = = 1/3*(/DA/ + /AB/) + 1/3*(/DA/ + /AC/) + 1/3*/DA/ = 1/3*/DA/ + + 1/3*/DB/ + 1/3*/DC/ = 1/3*(/a/+/b/+/c/). Отсюда находим скалярный квадрат вектора /DO4/ : (DO4)2=1/9*(a2+b2+c2+2/a/*/b/+2/a/*/c/+2/b/*/c/). Обозначив a1=|a|, b1=|b|, c1=|c|, a2=|BC|, b2=|AC|, c2=|AB| и воспользовавшись тем, что /AB/=/b/-/a/, /BC/=/c/-/b/, /CA/=/a/-/c/, можно DO4 выразить в виде (DO4)2= 1/3*((a1)2+(b1)2+(c1)2) + 1/9*((a2)2+(b2)2+(c2)2
Вы можете изучить и скачать доклад-презентацию на тему Тетраэдр. Презентация на заданную тему содержит 20 слайдов. Для просмотра воспользуйтесь проигрывателем, если материал оказался полезным для Вас - поделитесь им с друзьями с помощью социальных кнопок и добавьте наш сайт презентаций в закладки!

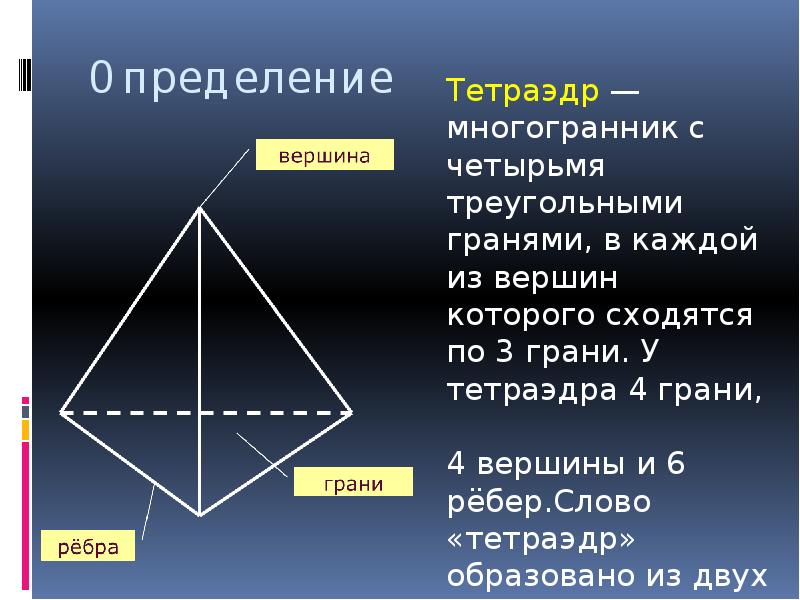
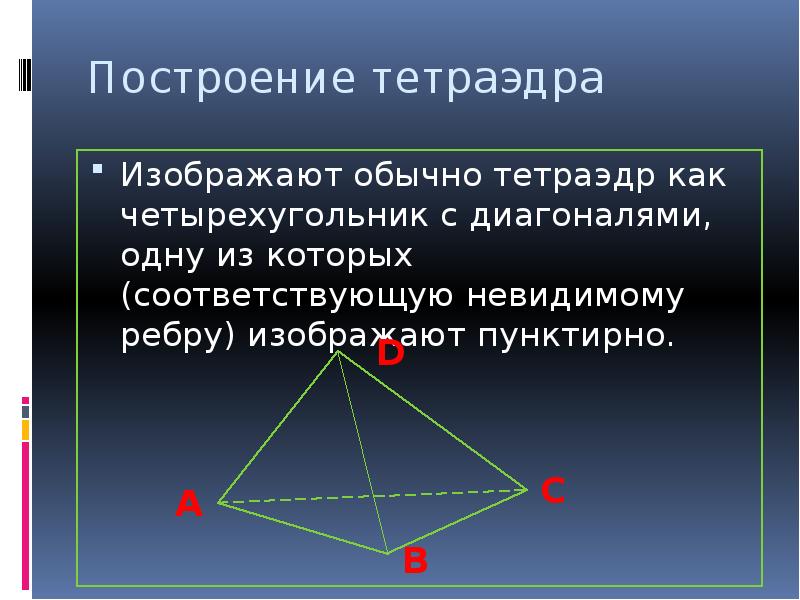















Построение тетраэдра Изображают обычно тетраэдр как четырехугольник с диагоналями, одну из которых (соответствующую невидимому ребру) изображают пунктирно.
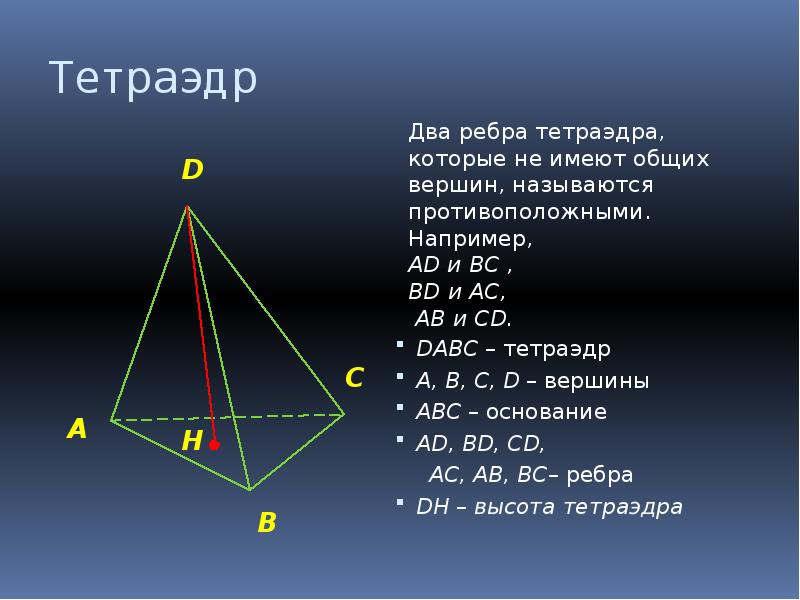
Тетраэдр DАВС – тетраэдр А, В, С, D – вершины АВС – основание АD, ВD, СD, АС, АВ, ВС– ребра DH – высота тетраэдра
Определения медианы, бимедианы(средние линии) и высоты тетраэдра Отрезок, соединяющий вершину тетраэдра с точкой пересечения медиан противоположной грани, называется его медианой, опущенной из данной вершины. Отрезок, соединяющий середины скрещивающихся рёбер тетраэдра, называется его бимедианой, соединяющей данные рёбра. Отрезок, соединяющий вершину с точкой противоположной грани и перпендикулярный этой грани, называется его высотой, опущенной из данной вершины.
Высота тетраэдра Высота тетраэдра — равна корню квадратному из двух третих, помноженному на длину ребра тетраэдра
Типы тетраэдров Равногранный тетраэдр – это тетраэдр, у которого все грани – равные между собой треугольники. Ортоцентрический тетраэдр – это тетраэдр, у которого все высоты, опущенные из вершин на противоположные грани, пересекаются в одной точке. Прямоугольный тетраэдр – это тетраэдр, у которого все ребра, прилежащие к одной из вершин, перпендикулярны между собой. Правильный тетраэдр – это тетраэдр, у которого все грани — равносторонние треугольники. Соразмерный тетраэдр, бивысоты которого равны. Инцентрический тетраэдр –это тетраэдр, у которого отрезки, соединяющие вершины тетраэдра с центрами окружностей, вписанных в противоположные грани, пересекаются в одной точке.
Правильный тетраэдр Тетраэдр, все четыре грани которого — равные правильные треугольники, называется правильным тетраэдром . Правильный тетраэдр — это частный случай правильной треугольной пирамиды.
Все четыре грани правильного тетраэдра – правильные треугольники. Если длину ребра правильного тетраэдра обозначить a, то можно вычислить:
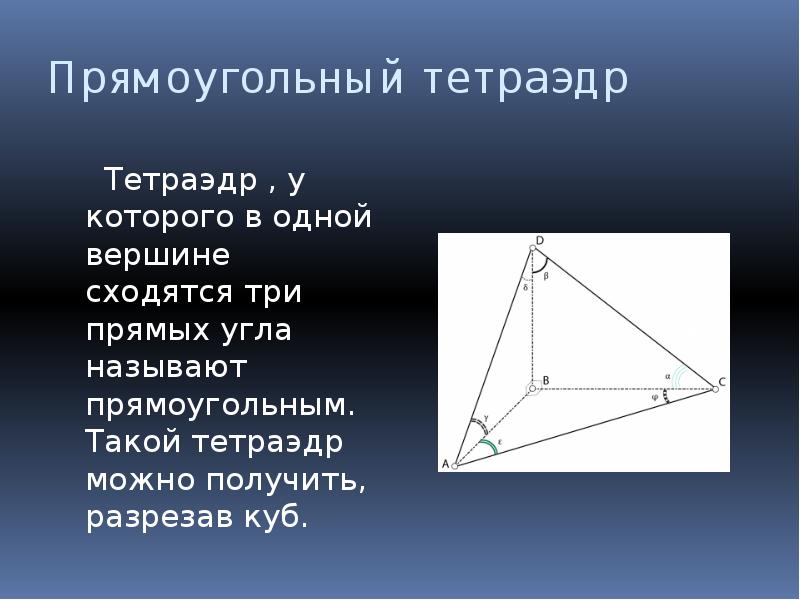
Прямоугольный тетраэдр Тетраэдр , у которого в одной вершине сходятся три прямых угла называют прямоугольным. Такой тетраэдр можно получить, разрезав куб.
Свойство тетраэдра Каждая его вершина является вершиной трех треугольников. А значит, сумма плоских углов при каждой вершине будет равна 180º. В правильный тетраэдр можно вписать октаэдр. Правильный тетраэдр можно вписать в икосаэдр, притом, четыре вершины тетраэдра будут совмещены с четырьмя вершинами икосаэдра. Правильный тетраэдр можно вписать в куб двумя способами, притом четыре вершины тетраэдра будут совмещены с четырьмя вершинами куба.
Тетраэдры в живой природе Некоторые плоды, находясь вчетвером на одной кисти, располагаются в вершинах тетраэдра, близкого к правильному. Такая конструкция обусловлена тем, что центры четырёх одинаковых шаров, касающихся друг друга, находятся в вершинах правильного тетраэдра. Поэтому похожие на шар плоды образуют подобное взаимное расположение. Например, таким образом могут располагаться грецкие орехи.
Тетраэдры в строительстве Тетраэдр образует жёсткую, статически определимую конструкцию. Тетраэдр, выполненный из стержней, часто используется в качестве основы для пространственных несущих конструкций пролётов зданий, перекрытий, балок, ферм, мостов и т. д. Стержни испытывают только продольные нагрузки.
Уголковый отражатель Уголковый отражатель — устройство в виде прямоугольного тетраэдра со взаимно перпендикулярными отражающими плоскостями. Излучение, попавшее в уголковый отражатель, отражается в строго обратном направлении. Используется:для точного измерения расстояний (для лазерной локации Луны, ИСЗ; топосъемке, строительстве); для возврата излучения точно назад (катафот, радиоэлектронная борьба).
Тетраэдры в микромире Молекула метана СН4 Молекула аммиака NH3 Алмаз C — тетраэдр с ребром равным 2,5220 ангстрем Флюорит CaF2, тетраэдр с ребром равным 3, 8626 ангстрем Сфалерит, ZnS, тетраэдр с ребром равным 3,823 ангстрем Комплексные ионы [BF4] -, [ZnCl4]2-, [Hg(CN)4]2-, [Zn(NH3)4]2+ Силикаты, в основе структур которых лежит кремнекислородный тетраэдр [SiO4]4-
Lipton tea & тетраэдр Чайная компания Lipton для разнообразия формы пакетиков для чая теперь выпускает их в виде тетраэдра

Многогранник относится к правильным многогранникам и является одним из пяти Платоновых тел .
Тетраэдр имеет следующие характеристики:
- Тип грани – правильный треугольник;
- Число сторон у грани – 3;
- Общее число граней – 4;
- Число рёбер, примыкающих к вершине – 3;
- Общее число вершин – 4;
- Общее число рёбер – 6;
Правильный тетраэдр составлен из четырех равносторонних треугольников. Каждая его вершина является вершиной трех треугольников. Следовательно, сумма плоских углов при каждой вершине равна 180°.
Тетраэдр не имеет центра симметрии, но имеет 3 оси симметрии и 6 плоскостей симметрии.
Является ли тетраэдр пирамидой? Да, тетраэдр это треугольная пирамида у которой все стороны равны.
Может ли пирамида быть тетраэдром? Только если это пирамида с треугольным основанием и каждая из её сторон равносторонний треугольник.
Отметим, что очень редко, но встречаются геометрические тела, составленные не из правильных треугольников, и их тоже называют тетраэдры, так как они имеют четыре грани.
Математические характеристики тетраэдра

Тетраэдр может быть помещен в сферу (вписан), так, что каждая из его вершин будет касаться внутренней стенки сферы.
Радиус описанной сферы тетраэдра определяется по формуле:
, где a - длина стороны.

Сфера может быть вписана внутрь тетраэдра.
Радиус вписанной сферы тетраэдра определяется по формуле:


Площадь поверхности тетраэдра
Для наглядности, площадь поверхности тетраэдра можно представить в виде площади развёртки. Площадь поверхности можно определить как площадь одной из сторон тетраэдра (это площадь правильного треугольника) умноженной на 4. Либо воспользоваться формулой:

Объем тетраэдра определяется по следующей формуле:

Высота тетраэдра определяется по следующей формуле:
Расстояние до центра основания тетраэдра определяется по формуле:
Вариант развертки
Тетраэдр можно изготовить самостоятельно. Бумага или картон самый подходящий вариант. Для сборки потребуется бумажная развёртка - единая деталь с линиями сгибов.
Древнегреческий философ Платон ассоциировал тетраэдр с "земным" элементом огонь, поэтому для построения модели этого правильного многогранника мы выбрали красный цвет.

Заметим, что это не единственный вариант развертки.
Для построения модели Вы можете скачать развертку в формате pdf и распечатать на листе формата А4:
- если Вы предполагаете распечатать на цветном принтере - цветная развертка
- если Вы предполагаете использовать для сборки цветной картон - развертка
Видео. Тетраэдр из набора "Волшебные грани"


Вы можете изготовить модель тетраэдра воспользовавшись деталями для сборки из набора "Волшебные грани".
Сборка многогранника из набора:
Подробная сборка от Алексея Жигулева (youtube-канал PRO)
Подробная сборка от Алексея Жигулева (youtube-канал PRO)
вращение готового многогранника:
Видео. Вращение всех правильных многогранников
Популярное
Приходилось ли вам сталкиваться с кубом, грани которого могут изменять свой цвет? Если да, то вполне вероятно вы уже сталкивались с.
Под руководством учителя математики Тимофеевой Татьяны Юрьевны ребята работали над проектом "Удивительный мир многогранников". Делали свои развертки и использовали развертки из.
Почтовые марки охватывают все значимые события в мире. Не обошли вниманием художники-филателисты и изображения многогранников. Почтовая марка, посвященная Леонарду Эйлеру с.
В микромире многогранники встречаются в виде молекул, вирусов и бактерий - простейших организмов. Например: фуллерены – шарообразные молекулы углерода С60 (рис.) - "кирпичики".
Для Вашего удобства мы снизили стоимость доставки наборов "Волшебные грани" в разы!

Тетраэдр (четырёхгранник) — многогранник, гранями которого являются четыре треугольника (от греческого tetra — четыре и hedra — грань).
- правильная треугольная пирамида — основание — равносторонний треугольник, все боковые грани — одинаковые равнобедренные треугольники (Рис. 3);
из определения правильного многогранника следует, что все рёбра тетраэдра имеют равную длину, а грани — равную площадь.

Две грани параллелепипеда, имеющие общее ребро, называются смежными , а не имеющие общих рёбер — противоположными .
Обычно выделяют какие-нибудь две противоположные грани и называют их основаниями , а остальные грани — боковыми гранями параллелепипеда.
Отрезок, соединяющий две вершины, не принадлежащие одной грани, называется диагональю параллелепипеда (Рис. 5).

Прямой параллелепипед, у которого основанием тоже является прямоугольник, называется прямоугольным параллелепипедом.

Длины непараллельных рёбер прямоугольного параллелепипеда называются его линейными размерами (измерениями).
Плоскостью сечения многогранника можно назвать любую плоскость, по обе стороны которой находятся точки многогранника.

У параллелепипеда \(6\) граней, поэтому сечением этого многогранника может быть треугольник (Рис. 9), четырёхугольник ( Рис. 10), пятиугольник (Рис. 11) или шестиугольник (Рис. 12).
| Рис. 9 | Рис. 10 | Рис. 11 | Рис. 12 |


6. через точку \(N\) в плоскости основания NL ∥ MP , так как линии пересечения параллельных плоскостей с третьей плоскостью должны быть параллельны;
Читайте также:

