Реферат на тему окружность и прямая

Обновлено: 03.07.2024

Круг и окружность – одни из самых древнейших геометрических фигур, философы древности придавали им большое значение. Круг – воплощение нескончаемого Времени и Пространства, символ всего сущего, Вселенной. “Из всех фигур прекраснейшая – круг”, – считал Пифагор.

Вокруг нас много круглых предметов. Представьте себе на секунду, что вдруг случилась беда: на Земле исчезло все круглое! Казалось бы – пусть все будет квадратным. Разве нельзя прожить без круглых труб, а к квадратным колесам нельзя привыкнуть? Можно ли вообще представить жизнь человека без использования круга? Почему так много тел имеют круглую форму? Чтобы найти ответы на все эти вопросы, в первую очередь, необходимо рассмотреть историю возникновения этих понятий и дальнейшее их развитие.

История возникновения и развития геометрических понятий “круг” и “окружность”.

Для первобытных людей важную роль играла форма окружавших их предметов. По форме и цвету они отличали съедобные грибы от несъедобных, пригодные для построек породы деревьев от тех, которые годятся лишь на дрова, вкусные орехи от горьких и т.д. Особенно вкусными казались им орехи кокосовой пальмы, похожие на шар. Специальных названий для геометрических фигур, конечно, не было. Говорили: “такой же, как кокосовый орех” или “такой же, как соль” и т.д. Так, овладевая окружающим их миром, люди знакомились с простейшими геометрическими фигурами.

Круглые тела еще в древности заинтересовали человека. В Древнем Египте для постройки знаменитых египетских пирамид никаких технических сооружений еще не было. Даже шлифовать огромные каменные глыбы приходилось вручную, а перемещали их с помощью бревен круглой формы. Заметили, что перекатка проще, если взять кусок дерева с почти одинаковой толщиной в начале и в конце. Так люди познакомились с одним из важнейших тел – цилиндром. Скалками цилиндрической формы пользовались и женщины, раскатывая белье после стирки. Перевозить грузы на катках было довольно тяжело, потому что сами древесные стволы весили много. Чтобы облегчить работу, стали вырезать из стволов тонкие круглые пластинки, которые катились уже легче и с их помощью перетаскивали грузы. Так появилось первое колесо. К сожалению, неизвестен непосредственный изобретатель колеса.

Не только в процессе работы люди знакомились с различными фигурами. Издавна они любили украшать себя, свою одежду, свое жилище. И многие, созданные давным-давно украшения, имели ту или иную форму. Бусинки были шарообразными, браслеты и кольца имели форму окружности. Древние мастера научились придавать красивую форму бронзе, золоту, серебру, драгоценным камням. Художники, расписывавшие дворцы, тоже использовали окружность. Со времени изобретения гончарного круга люди научились делать круглую посуду – горшки, вазы, амфоры. Круглыми были и колонны, подпирающие здания.

Математические знания египтян и вавилонян были разрозненные и представляли собой свод правил, проверенных практикой. В Древней Греции все разрозненные знания привели в систему, геометрия стала бурно развиваться как наука. Только в Древней Греции “окружность” и “круг” получили свои названия, почти все названия геометрических фигур греческого происхождения, как и само слово геометрия (“гео” – земля, а “метрио” – мерить). Однако эти слова вошли в русский язык не непосредственно с греческого, а через латинский язык.

В Древней Греции многие свойства фигур, в том числе круга и окружности были сформулированы в виде теорем и доказаны. Наиболее удачно была изложена геометрия, как наука о свойствах геометрических фигур, греческим ученым Евклидом (III в. до н. э.) в своих книгах “Начала”. В течение многих веков “Начала” были единственной учебной книгой, по которой молодежь изучала геометрию. И даже сейчас, в наше время, учебники написаны под большим влиянием “Начал” Евклида.

Окружность и круг – это плоские фигуры . Мы живем в мире трех измерений. А в какое геометрическое тело превратятся окружность и круг, если попадут в пространство? Это сфера и шар. “Сфера” – произошло от греческого слова “сфайра”, в переводе – “мяч”. Кроме этого геометрия пространства рассматривает и другие круглые тела – это “цилиндр” (от греческого слова “кюлиндрос”, что означает “валик”, “каток”) и “конус” (от греческого слова “конос”, означающего “сосновая шишка”). Самым важным среди круглых тел был шар.

Итак, в Древней Греции круг и окружность считали венцом совершенства. “В каждой своей точке окружность устроена одинаковым образом, что позволяет ей двигаться самой по себе”. Это свойство окружности стало толчком к возникновению колеса (Приложение 5). (Приложение 2).

Круг – “циркулус” – латинское слово, от него же и “циркуль”, без которого бы мы не построили круг. Циркуль и линейка – самые старые чертежные инструменты на Земле. (Приложение 3.)

Элементы окружности и круга (Приложение 2):

Радиус окружности – это отрезок, соединяющий центр окружности с любой ее точкой (по-латыни – спица колеса).

Диаметр окружности – это хорда, проходящая через центр окружности (с греческого – “поперечник”).

Хорда окружности – отрезок, соединяющий любые две точки на окружности (с греческого– “струна”).

Дуга окружности – это часть окружности, ограниченная двумя точками.

Часто в практических задачах нужно узнать длину окружности. А как измерить длину окружности, если сама окружность – кривая линия, а единица измерения длины – отрезок? Есть несколько способов измерения длины окружности (Приложение 1).

Однако эти способы непосредственного измерения длины окружности малоудобны и дают приближенные результаты. Поэтому уже с древних времен начали искать более совершенные способы измерения длины окружности. В процессе измерений заметили, что между длиной окружности и длиной ее диаметра имеется определенная зависимость: С:d ≈ 3,1.

Многие ученые – математики пытались доказать, что это отношение есть число постоянное, не зависящее от размеров окружности, его стали обозначать греческой буквой π-ο ервая буква греческого слова “периферия” – круг.

С:d = π, где С – длина окружности, d – длина диаметра, отсюда и формула длины окружности C = πd или C = 2πr.

Изучив исследования ученых математиков, мы провели следующие измерения и вычисления:

1. Вычисление числа пи : а) с помощью тонкой нити измерили длину окружности С некоторых предметов быта; б) чтобы точнее найти длину диметра d, приложили этот предмет к листу бумаги и обвели карандашом, вырезали, свернули пополам, линия сгиба – это диаметр, измерили его с помощью линейки; в) нашли отношение С:d, данные занесли в таблицу:

Предметы	Длина окружности С	Диаметр d	Отношение С:d
Стакан	22 см	7 см	3.1428
Ведро	82 см	26 см	3.1538
Тарелка	62 см	19,5 см	3,1794
Кастрюля	69 см	22 см	3.1363
Бидон	52 см	16,5 см	3,1515

2. Границы значения числа пи: а) с помощью циркуля вписали круг в квадрат: если диаметр равен 1,то длина окружности равна π . Периметр квадрата со стороной 1 равен 4. Значит π меньше 4. (Приложение 6. Рис.1). б) в этот же круг вписали правильный шестиугольник: диаметр круга снова 1, длина окружности равна π . Сторона правильного шестиугольника равна радиусу, т.е.0,5,а периметр равен 6·0,5=3,значит π больше 3 (Приложение 6. Рис.2).

В результате мы убедились, что отношение длины окружности к ее диаметру (число π) есть число постоянное и 3 ‹ π ‹ 4 ,т.е. мы подтвердили исследования ученых – математиков.

Одна из загадок числа π состоит в том, что оно не может быть выражено какой – либо точной дробью. История числа π достойна восхищения, многие математики затратили на его вычисления не один десяток лет. Уточнялись нижняя и верхняя оценки числа и предпринимались неудачные попытки представить π в виде дроби и, таким образом, окончательно найти его значение (Приложение 4). Пока рекорд принадлежит японскому математику, в 2004 году – Ясума Канада из Токио рассчитал число π на компьютере до 1,24 триллиона знаков.

π -3,141 592 653 589 793 238 462 643 383279 502 884197 169 399 375 105 ….

Зачем нужно π, да еще с такой точностью? Число π чрезвычайно важно для ученых и инженеров. Все, что круглое и все, что движется по кругу (как колеса или планеты), содержит π. Без π люди не могли создать автомобили, понять движение планет или сосчитать сколько гороха поместится в консервную банку. Но загадка таинственного числа не разрешена вплоть до сегодняшнего дня, и, по-прежнему, волнует ученых. В настоящее время с числом π связано труднообозримое множество формул, математических и физических фактов. Их количество продолжает стремительно расти. Все это говорит о возрастающем интересе к важнейшей математической константе, изучение которой насчитывает уже более двадцати двух веков.

Изучив литературу и проделав собственные измерительные исследования с окружностью и кругом, мы пришли к следующим выводам: окружность и круг – это удивительно гармоничные фигуры. Окружность – единственная кривая, которая может “скользить сама по себе”, вращаясь вокруг центра. Это свойство окружности дает ответ на вопросы, почему для ее вычерчивания используют циркуль, и почему колеса делают круглыми, а не квадратными или треугольными.

Круг в окружающей жизни.

Исследуя вопрос о роли круга в окружающей жизни, мы провели анкетирование обучающихся 5-9 классов и педагогов МО ШИСП (всего 90 человек):

Какие круглые тела вы встречаете в окружающей жизни?
Какое значение имеет круг в других науках?
Какие практические задачи повседневной жизни решаются, используя знания о круге и окружности?
Как вы считаете, почему встречается так много круглых тел в природе?

Ответы на первый вопрос представлены в презентации.

Круговые процессы-циклы: круговорот воды и веществ в природе.

Круглую форму имеют клетки крови, цилиндрическую – клетки многих желез.

Стебли растений и стволы деревьев, кости человека – круглые.

Кровообращение идет по кругу.

Овощи и фрукты имеют шарообразную или конусовидную форму.

От слова круг образовано множество различных слов: круглый, кругленький, округлить, округлиться, округлый, кругом, вокруг, окружать, кружить и многое другое.

Проанализировав ответы на третий вопрос анкеты, мы поняли, что знания о круге и окружности позволяют человеку решать многие практические задачи в повседневной жизни: разбить клумбу или фонтан, сделать круглую крышу, окно или крышку, сшить головной убор, связать салфетку, сделать елочную игрушку, сделать выкройку платья или юбки, нарисовать узор и т.п.

Таким образом, круг в жизни человека имеет очень важную роль, и в жизни без круглых предметов обойтись невозможно.

Не все, кого мы анкетировали, смогли дать ответ на четвертый вопрос.

Здесь мы помещаем самые интересные и распространенные ответы:

Только круглые предметы могут катиться, и поэтому их легче перемещать.
Потому что, куда бы мы не пошли, мы возвращаемся, т.е. идем по кругу.
У круга нет углов, и поэтому он удобен в применении, например, круглые монеты не могут порвать карман, о них не уколешься, не порежешься.
Мячик не может быть квадратным, он не будет отпрыгивать.
Посуду делали из глины, и округлую форму было легче придать, чем квадратную. Круглую посуду легче мыть, не надо выскребать из углов, в ней удобней размешивать.
Легче изготовить круглое, чем угловатое. Многие технические процессы легче для тел вращения.
На круглую форму идет меньше материала, чем на квадратную.
Круглая крышка люка никогда не провалится, в отличие от квадратной.
Все банки и крышки круглой формы, т.к. каждая точка окружности является точкой концентрации напряжения, и ее легко открыть, у прямоугольной формы такими точками являются только углы.
Потому ,что солнце круглое, а без солнца мы не могли бы существовать.
Круглая форма универсальна в природе.

Почему же на самом деле встречается так много круглых тел? Мы обратились к научным источникам. На этот вопрос можно ответить, рассмотрев мыльный пузырь, т.к. он идеально круглой формы. Силы поверхностного натяжения не дают лопнуть мыльному пузырю и стремятся придать мыльному пузырю максимально компактную форму. Самая компактная форма в природе – это шар. При шарообразной форме воздух внутри пузыря равномерно давит на все участки его внутренней стенки.

В небе много круглых объектов: Солнце, Луна, планеты, звезды. Почему не быть хотя бы одной некруглой планете? Ну, пусть одна, будет кубическая или пирамидальная. Но это невозможно? Есть сила, которая во всей Вселенной превращает миры в гладкие шары. Эта сила – сила тяготения. Каждый предмет имеет свою гравитацию, притягивает к себе другие тела, а также и свои части. Чем больше тело, тем сила тяжести увеличивается. Земля наша огромная, поэтому она имеет свою большую силу тяжести, которая заставляет притягиваться все к ее центру, а тело преобразовываться в шар. Если бы в силу каких-то причин удалось изменить нашу планету и придать ей иную форму, не шара, то спустя некоторое время она снова стала бы шарообразной. С телами на земле это не происходит, потому что их сила очень маленькая и сила тяжести Земли препятствует этому. Но если взять, например, каплю воды и запустить в космос, она сразу же преобразуется в шар. Именно жидкость способна преобразовываться в шарообразную форму. Земля состоит в основном из магмы (жидкости) поэтому и имеет форму шара.

Таким образом, мы пришли к выводам, что сама природа выбирает эту удобную и компактную форму – шара.

Кроме того, окружность и круг в виде сферы и шара – самая распространенная форма во Вселенной.

Круг и окружность – это еще и траектория движения Земли вокруг Солнца, это перемещение звезд на небе, это цикличность всех процессов, происходящих в мире. Если бы необходимо было бы выбрать форму, наиболее точно передающую устройство мира, то это были бы окружность и круг.

Изучив научную литературу, мы сделали вывод, что с незапамятных времен люди используют в своей жизни круг.

1. Около 3300 года до нашей эры стали применять гончарный круг, делать круглую посуду – тарелки, вазы, кастрюли, горшки, сковородки. У посуды есть окружность (верхний край) и круг (дно).

2. Мы не можем представить свою жизнь без машин: автобус, трактор, велосипед, швейная, стиральная и пишущая машинки, самолет, вездеход, луноход, различные станки, подъемный кран…Они не похожи друг на друга, но присмотримся к ним повнимательнее. Есть у них у всех похожие части – детали, и одна из них – колесо. Сначала колеса были круглые и гладкие, чтобы по земле легко катились, а потом человек придумал много разных колес. Зубчатые колеса спрятаны внутри многих машин, одно колесо заставляет вращаться другое, колеса с желобком –блоки, помогающие поднимать тяжелые грузы. Машины из века в век совершенствовались и совершенствуются, но неизменным остается использование в них колеса, как основной детали.

3. Круг и окружность широко применяются в архитектуре и искусстве: круглые арки, своды, купола. Круг – это форма кочевых шатров и поселений, у многих народов символизирующая динамизм и бесконечное движение в противовес квадратам домов, участкам земли и городам оседлых и зерносеющих народов. Еще древние греки обнаружили, что с помощью циркуля и линейки можно построить множество фигур, включая шестиугольники, квадраты и другие правильные многоугольники, и создавать волшебные узоры.

4. Необозрима сфера применения круга в математике: тригонометрический круг, круги Эйлера, задачи на построение, круговые диаграммы и т.д. Многие приборы имеют круглую шкалу, в математике таким прибором является транспортир (Приложение 7).

Есть в математике задачи, которые до сих пор не разрешены, например, знаменитая задача о “квадратуре круга” – о построении квадрата, равновеликого данному кругу и т.д.

5. Картинки с волшебными кругами люди используют в медицинских целях, когда на них смотришь, кажется, что они двигаются. Если смотреть на них несколько минут, то проходит головная боль (Приложение 8).

6. Также человек использует круг, как универсальный символ, означающий целостность, непрерывность, первоначальное совершенство, бесконечность, отсутствие начала и конца, верха и низа, цикличность, повторяемость, завершенность. Три концентрических круга символизируют прошлое, настоящее и будущее; три сферы земли: землю, воздух и воду; небесные миры, землю и преисподнюю; фазы луны; восходящее, полуденное и заходящее солнце. Многие народы используют круг в религии, как символ связи земного с космосом.

В последнее время в разных местах земного шара стали появляться круги на полях, которые создают посланцы иных миров, желая о чем-то предупредить землян. (Приложение 9).

7. В энциклопедии мы нашли еще много понятий связанных с кругом: кругловязальная машина, круглочулочный автомат, круглогубцы, кругломер, “круговая система” в спорте, кругозор, круг друзей, круг общения, спасательный круг, святой круг, спиритический круг, круговая оборона, круговая порука, круглосуточная аптека, круги вокруг глаз.

Прямая, имеющая с окружностью только одну общую точку.

Касательная перпендикулярна к радиусу окружности, проведённому в точку касания

Прямая, пересекающая окружность в двух точках

Окружность

Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки - центра окружности

Конечная часть плоскости, ограниченная окружностью

Отрезок, соединяющий центр окружности с любой точкой окружности

Отрезок, соединяющий две любые точки окружности

Хорда, проходящая через центр окружности.

Диаметр является самой длинной хордой окружности

Прямая, имеющая с окружностью только одну общую точку.

Касательная перпендикулярна к радиусу окружности, проведённому в точку касания

Прямая, пересекающая окружность в двух точках

Свойства хорд и дуг окружности

Фигура	Рисунок	Свойство
Диаметр, перпендикулярный к хорде		Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам.
Диаметр, проходящий через середину хорды		Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам.
Равные хорды		Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности.
Хорды, равноудалённые от центра окружности		Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны.
Две хорды разной длины		Большая из двух хорд расположена ближе к центру окружности.
Равные дуги		У равных дуг равны и хорды.
Параллельные хорды		Дуги, заключённые между параллельными хордами, равны.

Диаметр, перпендикулярный к хорде

Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам.

Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам.

Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности.

Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны.

Большая из двух хорд расположена ближе к центру окружности.

У равных дуг равны и хорды.

Дуги, заключённые между параллельными хордами, равны.

Теоремы о длинах хорд, касательных и секущих

Произведения длин отрезков, на которые разбита каждая из хорд, равны:

Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.

Произведения длин отрезков, на которые разбита каждая из хорд, равны:

Пересекающиеся хорды

Произведения длин отрезков, на которые разбита каждая из хорд, равны:

Доказательства теорем о длинах хорд, касательных и секущих

Теорема 1 . Предположим, что хорды окружности AB и CD пересекаются в точке E (рис.1).

Тогда справедливо равенство

Доказательство . Заметим, что углы BCD и BAD равны как вписанные углы, опирающиеся на одну и ту же дугу. Углы BEC и AED равны как вертикальные. Поэтому треугольники BEC и AED подобны. Следовательно, справедливо равенство

откуда и вытекает требуемое утверждение.

Теорема 2 . Предположим, что из точки A , лежащей вне круга, к окружности проведены касательная AB и секущая AD (рис.2).

Точка B – точка касания с окружностью, точка C – вторая точка пересечения прямой AD с окружностью. Тогда справедливо равенство

Доказательство . Заметим, что угол ABC образован касательной AB и хордой BC , проходящей через точку касания B . Поэтому величина угла ABC равна половине угловой величины дуги BC . Поскольку угол BDC является вписанным углом, то величина угла BDC также равна половине угловой величины дуги BC . Следовательно, треугольники ABC и ABD подобны (угол A является общим, углы ABC и BDA равны). Поэтому справедливо равенство

откуда и вытекает требуемое утверждение.

Теорема 3 . Предположим, что из точки A , лежащей вне круга, к окружности проведены секущие AD и AF (рис.3).

Точки C и E – вторые точки пересечения секущих с окружностью. Тогда справедливо равенство

Доказательство . Проведём из точки A касательную AB к окружности (рис. 4).

Точка B – точка касания. В силу теоремы 2 справедливы равенства

откуда и вытекает требуемое утверждение.

Теорема о бабочке

Теорема о бабочке . Через середину G хорды EF некоторой окружности проведены две произвольные хорды AB и CD этой окружности. Точки K и L – точки пересечения хорд AC и BD с хордой EF соответственно (рис.5). Тогда отрезки GK и GL равны.

Доказательство . Существует много доказательств этой теоремы. Изложим доказательство, основанное на теореме синусов, которое, на наш взгляд, является наиболее наглядным. Для этого заметим сначала, что вписанные углы A и D равны, поскольку опираются на одну и ту же дугу. По той же причине равны и вписанные углы C и B . Теперь введём следующие обозначения:

Воспользовавшись теоремой синусов, применённой к треугольнику CKG , получим

Воспользовавшись теоремой синусов, применённой к треугольнику AKG , получим

Данная тема представляет определенный интерес, так как её истоки относятся к древности. Окружность — самая простая из кривых линий. Это одна из древнейших геометрических фигур, которая всегда привлекала внимание художников, архитекторов. Философы древности придавали ей большое значение.

Вложение	Размер
issledovat_rabota_yulya.docx	124.94 КБ

Предварительный просмотр:

Окружность и круг

Автор: Алексашина Юлия

ученица 5 класса

ГБОУ ООШ №3 г. Жигулевск

Руководители: Царькова Д.А.

ГБОУООШ №3 г.о.Жигулевск

г. Тольятти, 2013

Основная цель работы: исследование окружности и круга.

Основные задачи исследования:

1) познакомиться с понятиями: окружность, центр и радиус окружности, диаметр, хорда окружности.

2) выяснить, на какое наибольшее число частей можно разделить окружность тремя прямыми.

3) выяснить, существует ли круг, чтобы его площадь и длина окружности выражались одним и тем же числом.

4) рассмотреть взаимное расположение на плоскости прямой и окружности.

5) рассмотреть взаимное расположение на плоскости двух окружностей.

Основные методы решения поставленных задач : метод наблюдения за числами; метод подбора и проб; чтение дополнительной литературы; составление таблиц и сравнение результатов; метод обобщения.

Часть 1. Основные понятия, используемые в работе

1.1. Понятие Окружности

Окружность — геометрическая фигура, состоящая из всех точек плоскости, расположенных на заданном расстоянии от данной точки.

Данная точка (O) называется центром окружности.

Любые две точки окружности делят ее на две части. Каждая из этих частей называется дугой окружности.

1.2. Длина окружности

Обозначим длину окружности буквой l , а ее диаметр буквой d и запишем формулу

Число π приблизительно равно 3.14

Более точное его значение π = 3,1415926535897932. Исходя из формулы выше, выведем, чему равна окружность, если известен диаметр d .

Если известен радиус r , то формула длины окружности будет выглядеть так:

1.3. Радиус окружности

Радиус окружности — это отрезок, соединяющий центр с какой-либо точкой окружности. Все радиусы имеют одну и ту же длину (по определению).
Определить радиус окружности можно по формуле:

1.4. Диаметр окружности

Хорда — отрезок, соединяющий две точки окружности. Хорда, проходящая через центр окружности, называется диаметром. Центр окружности является серединой любого диаметра. Определить диаметр окружности можно по формуле:

где R — радиус, D — диаметр, π — число π = 3,14.

Часть 2. Постановка и решение задач

2.1. Постановка первой задачи

Рассмотрим, на какое наибольшее число частей можно разделить окружность тремя прямыми.

Рассмотрев всевозможные варианты, можно сделать вывод о том, что наибольшее число частей, на которое можно разделить окружность тремя прямыми равно 7.

Итак, сделаем первый вывод : наибольшее число частей, на которое можно разделить окружность тремя прямыми равно 7.

2.2. Постановка второй задачи

Дан квадрат, периметр и площадь которого выражаются одним и тем же числом.

Пусть сторона квадрата равна Х, тогда Р=4Х , а S=X 2 .

Таким образом, можно сделать вывод, что при стороне квадрата равной 4, периметр и площадь будут выражаться одним целым числом.

Предположим, что существует круг, площадь и длина окружности которого выражаются одним числом.

Длина окружности вычисляется по формуле: L=2пR=пD

Площадь: S = πR 2 . π=3,14

Составим таблицу 1.

Из таблицы видно, что при радиусе равном 2 площадь и длина окружности, которого выражаются одним числом.

Итак, сделаем второй вывод: существует круг, площадь и длина окружности которого выражаются одним числом, радиус которого равен 2.

2.3. Постановка третей задачи

сравним длины окружностей, заменяя π числами и

Найдем длину окружности, если радиус равен 497 см.

2.4. Постановка четвертой задачи

При вычислении длины окружности в Древнем Вавилоне за π часто принимали число, равное 3. Сравним их ответ от настоящего ответа при нахождении длины окружности. R= 40

Сравнив полученные данные, можно сделать вывод, что при вычислении длины окружности в Древнем Вавилоне ответ меньше настоящего на 11,2.

2.5. Постановка пятой задачи

Рассмотрим всевозможные случаи взаимного расположения на плоскости прямой и окружности.

Если расстояние от центра окружности до прямой меньше радиуса окружности ( d ), то прямая и окружность имеют две общие точки. В этом случае прямая называется секущей по отношению к окружности.

Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют только одну общую точку. Такая прямая называется касательной к окружности , а их общая точка называется точкой касания прямой и окружности .

Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общих точек.

2.6. Постановка шестой задачи

Рассмотрим всевозможные случаи взаимного расположения на плоскости двух окружностей.

Окружности не имеют общих точек, но у них общий центр

Окружности имеют одну общую точку

Окружности имеют две общие точки

Окружности не имеют общих точек

2.7. Отличие окружности от круга

Окружность представляет собой бесчисленное множество точек, которые находятся на одинаковом расстоянии от одной единственной, называемой центром окружности. Соединенные между собой точки формируют кривую линию, которая и будет окружностью. Все точки, которые находятся на другом расстоянии от центра окружности, не будут находиться на этой линии, поэтому не будут входить в окружность. Соответственно, окружность – это геометрическая фигура, которая представляет собой определенную линию, а все, что находится внутри нее либо снаружи, к окружности не относится. По этой причине имеется четкое понятие, что окружность делит всю плоскость на две части – внутреннюю, ограниченную линией окружности, и внешнюю, безграничную, поскольку плоскость в общем понимании не имеет границ.

Круг является геометрической фигурой, граница которой состоит из бесчисленного множества точек, равноудаленных от центра круга. Все внутреннее пространство, а также центр круга принадлежат ему, таким образом, можно говорить о том, что круг представляет собой некую площадь пространства, ограниченную множеством точек. А поскольку эти точки равноудалены от центра, то границей круга будет окружность. Все внешнее пространство кругу не принадлежит, зато он охватывает всю ту часть плоскости, которая очерчена при помощи окружности.

Различия между кругом и окружностью не столь велики, поскольку эти фигуры представляют собой неисчисляемое количество точек плоскости, находящихся от одной центральной точки на одинаковом расстоянии. Но важным отличительным признаком является тот факт, что внутреннее пространство не принадлежит окружности, но обязательно является составной частью круга. Иными словами, круг представляет собой не только окружность, которая является его границей, но также и то бесконечное число точек, находящихся внутри этой окружности.

Можно сделать следующий вывод. Разница между кругом и окружностью заключается в следующем:

1. Окружность является лишь частью круга, его границей, в то время как круг является более обширной и полноценной фигурой;

2. Окружность – это кривая линия, состоящая из бесчисленного множества точек, равноудаленных от центра, а круг представляет собой не только сумму этих точек окружности, но также и все те точки, которые расположены внутри этой самой окружности.

Проведенная выше работа позволила мне сделать следующие выводы:

1. Наибольшее число частей, на которое можно разделить окружность тремя прямыми равно 7.

2. При стороне квадрата равной 4, периметр и площадь будут выражаться одним целым числом.

3. Существует круг, площадь и длина окружности которого выражаются одним числом, радиус которого равен 2.

4. Существует три случая взаимного расположения на плоскости прямой и окружности: прямая и окружность имеют две общие точки; прямая и окружность имеют только одну общую точку; прямая и окружность не имеют общих точек.

5. Существует четыре случая взаимного расположения на плоскости двух окружностей.

Так же выяснила, что разница между кругом и окружностью заключается в следующем:

1. Глейзер Г.И. История математики в школе 7-8 кл.: Пособие для учителей. –М.: Просвещение, 1982. С. 32.

3. Шарыгин И.Ф., Ерганжиева Л.Н. Наглядная геометрия: Учеб. пособие для учащихся 5-6 классов. – М.: МИРОС, 1995. С. 72—83.

Всё про окружность и круг

Окружность — это геометрическое место точек плоскости, равноудаленных от некоторой заданной точки (центра окружности). Расстояние между любой точкой окружности и ее центром называется радиусом окружности (радиус обозначают буквой R).
Значит, окружность — это линия на плоскости, каждая точка которой расположена на одинаковом расстоянии от центра окружности.

Кругом называется часть плоскости, ограниченная окружностью и включающая ее центр.

Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр окружности, представляет собой диаметр. Диаметр окружности равен ее удвоенному радиусу: D = 2R.

Точка пересечения двух хорд делит каждую хорду на отрезки, произведение которых одинаково: a1a2 = b1b2

Касательная к окружности всегда перпендикулярна радиусу, проведенному в точку касания.

Отрезки касательных к окружности, проведенные из одной точки, равны: AB = AC, центр окружности лежит на биссектрисе угла BAC.

Квадрат касательной равен произведению секущей на ее внешнюю часть

Центральный угол — это угол, вершина которого совпадает с центром окружности.

Дугой называется часть окружности, заключенная между двумя точками.

Мерой дуги (в градусах или радианах) является центральный угол, опирающийся на данную дугу.

Вписанный угол это угол, вершина которого лежит на окружности, а cтороны угла пересекают ее.

Вписанный угол равен половине центрального, если оба угла опираются на одну и ту же дугу окружности.
Внутренние углы, опирающиеся на одну и ту же дугу, равны.

Сектором круга называется геометрическая фигура, ограниченная двумя радиусами и дугой, на которую опираются данные радиусы.

Периметр сектора: P = s + 2R.

Площадь сектора: S = Rs/2 = ПR 2 а/360°.

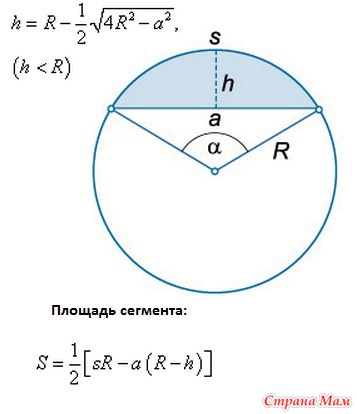
Сегментом круга называется геометрическая фигура, ограниченная хордой и стягиваемой ею дугой.

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3

Министерство образования и науки

Муниципальное общеобразовательное учреждение

Глава III .Построение окружности с помощью циркуля и линейки
3.1 Основные понятия………………………………………………………..19-21
3.2 Деление отрезков ………………………………………………………. 22-23
3.3 Известные задачи………………………………………………………. 24-26
3.4 Неразрешимые задачи. ……………………………………………………..27
3.5 Интересные факты…………………………………………………………. 28

Когда-то геометрия включала всю математику. Но математика росла и развивалась особенно бурно в последние 200 лет. Возникли новые направления: математический анализ, теория множеств, топология, совсем иначе стала выглядеть алгебра. Конечно, развивалась и геометрия, однако некоторые математики начали в последнее время относить ее к числу второстепенных математических направлений. Это мнение нашло свое отражение и в содержании школьных программ по математике. Как мало мы знаем о природе геометрии и об успехах, которые были достигнуты ее исследователями! Геометрия и сейчас обладает всеми теми достоинствами, за которые ее ценили педагоги прошлых поколений.

Самая простая из кривых линий – окружность. Это одна из древнейших геометрических фигур. Философы древности придавали ей огромное значение. Согласно Аристотелю, небесная материя, из которой состоят планеты и звезды, как самая совершенная, должна двигаться по самой совершенной фигуре – окружности. Сотни лет астрономы считали, что планеты двигаются по окружностям. Это ошибочное мнение было опровергнуто лишь в XVII в. учением Коперника, Галилея, Кеплера и Ньютона.

Цель данного реферата состоит в том, чтобы вспомнить некоторые из полузабытых вещей, касающихся окружностей и касательных к ним, вывести новые теоремы. Узнать способы деления отрезков с помощью циркуля и линейки.

Задача реферата: 1. Изучить понятия окружности и касательных. Особенности и свойства; 2. Окружность девяти точек; 3. Рассмотрение задач на деление отрезков с помощью циркуля и линейки.

1.1 Что такое окружность?

Окружность (рис.1) — геометрическое место всех точек плоскости, равноудалённых от заданной точки, называемой центром, на заданное неотрицательное расстояние , называемое её радиусом.

· Окружность диаметра AB — это фигура, состоящая из точек A, B и всех точек плоскости, из которых отрезок AB виден под прямым углом.

· Окружность — это фигура, состоящая из всех точек плоскости, для каждой из которых отношение расстояний до двух данных точек равно данному числу, отличному от единицы.

· Также фигура, состоящая из всех таких точек, для каждой из которых сумма квадратов расстояний до двух данных точек равна заданной величине, большей половины квадрата расстояния между данными точками.

Радиус (рис.2) — не только величина расстояния, но и отрезок , соединяющий центр окружности с одной из её точек.

( рис.2 ) ОА = r — радиус

Отрезок, соединяющий две точки окружности, называется её хордой. Хорда, проходящая через центр окружности, называется диаметром (рис.3).

(рис.3) АВ — диаметр

· Прямая, имеющая с окружностью ровно одну общую точку, называется касательной (рис.4) к окружности, а их общая точка называется точкой касания прямой и окружности.

(рис.4) а — касательная

Прямая, проходящая через две различных точки окружности, называется секущей (рис.5).

(рис.5) АВ – секущая

· Центральный угол (рис. 6)— угол с вершиной в центре окружности. Центральный угол равен градусной мере дуги, на которую опирается.

Вписанный угол (рис. 7) — угол, вершина которого лежит на окружности, а стороны пересекают эту окружность. Вписанный угол равен половине градусной меры дуги, на которую опирается.

1.3 Вписанная окружность.

Окружность называется вписанной в угол, если она лежит внутри угла и касается его сторон. Центр окружности, вписанной в угол, лежит на биссектрисе этого угла.

Окружность называется вписанной в выпуклый многоугольник, если она лежит внутри данного многоугольника и касается всех прямых, проходящих через его стороны.

Если в данный выпуклый многоугольник можно вписать окружность, то биссектрисы всех углов данного многоугольника пересекаются в одной точке, которая является центром вписанной окружности.

· В каждый треугольник можно вписать окружность, притом только одну.

· Центр O вписанной окружности называется инцентром, он равноудалён от всех сторон и является точкой пересечения биссектрис треугольника.

· Не во всякий четырехугольник можно вписать окружность (рис.10)

· В любом описанном четырехугольнике суммы противоположных сторон равны (АВ + С D = a + b + c + d , BC + AD = a + b + c + d , поэтому AB + CD = BC + AD ) (рис.11)

Окружность - это геометрическое место точек плоскости, равноудаленных от некоторой заданной точки (центра окружности). Расстояние между любой точкой окружности и ее центром называется радиусом окружности (радиус обозначают буквой R).
Значит, окружность — это линия на плоскости, каждая точка которой расположена на одинаковом расстоянии от центра окружности.

Кругом называется часть плоскости, ограниченная окружностью и включающая ее центр.

Точка пересечения двух хорд делит каждую хорду на отрезки, произведение которых одинаково: a1a2 = b1b2

Касательная к окружности всегда перпендикулярна радиусу, проведенному в точку касания.

Квадрат касательной равен произведению секущей на ее внешнюю часть

Центральный угол - это угол, вершина которого совпадает с центром окружности.

Дугой называется часть окружности, заключенная между двумя точками.

Мерой дуги (в градусах или радианах) является центральный угол, опирающийся на данную дугу.

Вписанный угол это угол, вершина которого лежит на окружности, а cтороны угла пересекают ее.

Периметр сектора: P = s + 2R.

Площадь сектора: S = Rs/2 = ПR 2 а/360°.

Сегментом круга называется геометрическая фигура, ограниченная хордой и стягиваемой ею дугой.

Скопируйте код и вставьте в окошко создания записи на LiveInternet, предварительно включив там режим "Источник"

+13 Зарегистрируйтесь и получите возможность оценивать материалы, общаться в комментариях и многое другое!')"> Зарегистрируйтесь и получите возможность оценивать материалы, общаться в комментариях и многое другое!')">

Lilit

05.01.2015

114

5 комментариев

Построим каркасный дом вашей мечты

Каркасный дом с гаражом на 2 авто V161 "Давис"

Каркасный дом с гаражом V200 "Цлантон"

Каркасный дом с террасой V193 "Гунтерсвилле"

Каркасный дом с мансардой V399 "Саннивейл"

В одном месте собраны все формулы, определения и теоремы касаемо окружности и круга, без которых решение многих геометрических задач просто не возможно - это к Вашему вопросу "зачем".

Хорошая вещь - эти ваши круги. В хозяйстве постоянно пользуюсь. Мне особенно про вписанный угол понравилось, как-то к шарнирам думаю приспособить. что-то там есть.

Вставка изображения

Можете загрузить в текст картинку со своего компьютера:

. или указать адрес картинки в интернете:

Загрузка списка альбомов.

Вставка изображения

Чаще всего на сайте читают:

Я отношусь к малочисленному виду "мамаша-пофигист". Учится ребенок, и ладно. Золотая медаль в доме уже есть, висит-пылится на видном месте. Свой мозг в головы дочерей все равно не вложишь, поэтому приходится обходиться заводской комплектацией. На каждое собрание прихожу с открытой душой новорожденного ребенка: закономерные вопросы других, ответственных мам, типа "как вы решали №768 со страницы 878787 по учебнику Засланца-Марсианского" вводят меня в ступор. Однако и меня не обошел стороной конфликт с учителем. Но я смогла решить его с наименьшими потерями. Как? Об этом расскажу в своей записи.

Квартиру мы купили еще в 2007 году, в 2008 сделали капитальный ремонт и благополучно отметили новоселье. Но две шестиметровые лоджии мы так и не отделали, не хватило денег. И как-то наш друг проронил такую фразу: Сразу не сделаете - уже никогда не сделаете! Поэтому мелкие недоделки по квартире я постаралась доделать пока свежо, а вот лоджии так и стояли до этой осени грустные и обшарпанные, такие как нам достались от предыдущих хозяев.

В передаче "Тайны Мира" сейчас говорили про волшебные свойства соды. Без всяких диет и упражнений полежала в ванной 20 минут и все, пара кило ушли.

У моего 16-летнего брата завелась девушка. И вот я совершенно случайно подслушала их разговор. Собрался братишка к пассии своей в гости и мой муж дает ему наставления. Муж - "Как придешь к ней домой сразу просись в туалет, не стесняйся. А там загляни под крышку унитаза. Если обнаружишь сам знаешь что, то смело сваливай от неряхи и стирай ее номер телефона".

Читайте также:

Реферат на тему окружность и прямая

Свойства хорд и дуг окружности

Теоремы о длинах хорд, касательных и секущих

Доказательства теорем о длинах хорд, касательных и секущих

Теорема о бабочке

Предварительный просмотр:

Всё про окружность и круг

Построим каркасный дом вашей мечты

Каркасный дом с гаражом на 2 авто V161 "Давис"

Каркасный дом с гаражом V200 "Цлантон"

Каркасный дом с террасой V193 "Гунтерсвилле"

Каркасный дом с мансардой V399 "Саннивейл"

Комментарии

Вставка изображения

Загрузка списка альбомов.

Вставка изображения

Чаще всего на сайте читают: