Реферат на тему геометрия римана

Обновлено: 02.07.2024

При решении задач практического характера и, в первую очередь, задач астрономии возникла сферическая геометрия в IV в. до н. э. Cферическая геометрия возникла позже евклидовой геометрии при решении задач практического характера. Выводы этой геометрии были необходимы путешественникам и мореплавателям, которые ориентировались по звёздам. Сведения о сфере использовались и при решении сугубо земных задач — вычислении географических координат, для составления географических карт, для нахождения курса корабля.

Актуальность выбора темы исследования обусловлена тем, что в настоящее время сферическая геометрия особенно широкое применение находит в астрономии, геодезии, навигации и картографии. Одной из задач данного исследования является сравнение свойств фигур на плоскости и фигур на сфере. Выдвигается гипотеза о том, что зависимости между элементами сферического треугольника выражаются формулами, отличными от формул евклидовой геометрии.

Результат исследования : существование геометрии Римана, отличной от евклидовой; применение геометрии Римана в жизни. Приведён алгоритм вычисления длины пути на зимовку перелётных птиц.

1 . Основные понятия сферической геометрии

Сферой называется множество точек пространства, расположенных на данном расстоянии от данной точки, называемой её центром. Плоскость, проходящая через центр сферы, называется диаметральной плоскостью . Диаметральная плоскость пересекает сферу по большой окружности (рис.1) . Любая плоскость, которая не проходит через центр сферы, пересекает сферу по малой окружности (рис.2) .

Так как через любые три точки пространства, не лежащие на одной прямой, проходит плоскость и притом единственная, то через любые две точки сферы А, В, не являющиеся диаметрально противоположными и центр сферы, точку О, проходит единственная диаметральная плоскость. Следовательно, через любые две точки сферы проходит единственная большая окружность (рис.3). Через две диаметрально противоположные точки сферы можно провести бесконечное множество больших окружностей (рис.4). Любые две большие окружности пересекаются в двух диаметрально противоположных точках сферы [1]. Между геометрией на сфере и геометрией на плоскости имеются существенные различия. Роль прямых на сфере отводится большим окружностям. Известно, что через любые две точки плоскости проходит единственная прямая; другими словами, никакие две прямые не могут пересечься в двух точках. Но, в отличие от плоскости, две сферические прямые обязательно пересекаются в двух диаметрально противоположных точках. Таким образом, в сферической геометрии просто не существует понятия параллельности. Это обстоятельство отличает сферическую геометрию от евклидовой. Еще одно отличие – сферическая прямая, т.е. большая окружность, замкнута, т.к. двигаясь по ней в одном и том же направлении, мы вернемся в исходную точку. Большая окружность делит сферу на две области; эти области называются полусферами , две большие окружности делят сферу на четыре области (рис.5). Так как три плоскости, пересекающиеся в одной точке, делят пространство на восемь областей, то три большие окружности, не пересекающиеся в одной точке, делят сферу на восемь областей: (ABC, ABC, ABC, ABC, ABC, ABC, ABC, ABC), те, на которые делят сферу большие окружности AB, AC и BC, причём точки A,B,C диаметрально противоположны точкам A,B,C (рис.6) .

2 . Сферический отрезок

Если две точки сферы А и В не являются диаметрально противоположными, то существует единственная плоскость, проходящая через центр сферы и эти две точки. Линия пересечения этой плоскости со сферой есть большая окружность. Точки А и В разбивают большую окружность на две части. Меньшая из двух дуг этой окружности, соединяющая точки А и В, является сферическим отрезком (рис.7).

С ферический отрезок, соединяющий две точки на сфере, короче любой другой линии на сфере, соединяющий эти две точки (рис.8) .

Длина сферического отрезка АВ равна радианной мере центрального угла AOB (рис.9). Таким образом, в сферической геометрии длины отрезков измеряются в радианах. Это ещё одно из отличий геометрии на сфере от евклидовой геометрии на плоскости.

3. Сферический многоугольник

Сферическим многоугольником называется часть сферы, ограниченная дугами больших окружностей, меньшими полуокружности. В отличие от плоскости, где треугольник является многоугольником с наименьшим числом сторон, на сфере имеются многоугольники с двумя сторонами называемые двуугольниками. Сферический двуугольник - фигура, образованная двумя полуокружностями больших окружностей сферы (рис.10). Вершины сферического двуугольника являются диаметрально противоположнымы точками сферы. Углы на сфере определяются следующим образом: Угол между плоскостями двух больших кругов называется двугранным углом. Он равен углу при вершине двуугольника, т.е. углу между сферическими отрезками (рис.11) .

4 . Сферический треугольник Среди всех сферических многоугольников наибольший интерес представляет сферический треугольник. Сферический треугольник — геометрическая фигура на поверхности сферы, образованная пересечением трёх больших окружностей (рис.12).

Или по-другому : сферическим треугольником называется фигура, образованная тремя дугами окружностей больших кругов, попарно соединяющих три точки [2].

Три больших окружности, которые пересекаются попарно в двух точках, образуют на сфере восемь сферических треугольников (рис.13). Зная элементы (стороны и углы) одного из них, можно определить элементы всех остальных, поэтому рассматривают соотношение между элементами одного треугольника, того, у которого все стороны меньше половины большой окружности. Как и в планиметрии, в сферической геометрии существуют определенные соотношения между сторонами и углами треугольников.

Следующие свойства сферического треугольника аналогичны свойствам плоского треугольника: а) в каждом сферическом треугольнике против большего угла лежит большая сторона; б) сумма любых двух сторон больше третьей стороны[3].

Однако, признаков равенства треугольников на сфере 4, а не 3. Добавляется четвёртый признак по равенству трёх углов. Подобных треугольников на сфере не существует.

Вот ещё удивление сферической геометрии: треугольник на сфере может иметь три прямых угла, если он ограничен двумя перпендикулярными меридианами и экватором.

5. Площадь сферического треугольника

Будем называть площадью сферической фигуры, по аналогии с площадью плоской фигуры, действительное число, удовлетворяющее следующим четырём требованиям:

площадь сферической фигуры является положительным числом (свойство позитивности);

площадь сферической фигуры не изменяется при движении (свойство инвариантности);

если сферическая фигура разбита на части, то площадь данной фигуры равна сумме площадей её частей (свойство аддитивности);

площадь всей сферы радиуса R равна 4R 2 (свойство нормировки) [4].

Для нахождения площади сферического треугольника используется теорема о площади двуугольника (рис.14).

Теорема : площадь двуугольника, углы, при вершинах которого равны , определяется формулой:

Три больших окружности, пересекаясь попарно в двух точках, образуют на сфере шесть двуугольников с вершинами в точках А, В, С (рис.13).

Например, окружности, проходящие через точки С, В и через точки С, А определяют два двуугольника с углами С. Вершин три, таким образом, получается шесть двуугольников, два с углом А, два – с углом В и два – с углом С.

Треугольник АВС равен диаметрально противоположному треугольнику А'В'С'. Треугольник АВС входит в двуугольник с верщиной А, с вершиной В и с вершиной С, т.е. повторяется трижды. Треугольник А'В'С' также повторяется трижды. Остальные точки сферы входят только в один двуугольник. Поэтому сумма площадей шести двуугольников равна площади S всей сферы плюс учетверённая площадь S() треугольника АВС, т.е. 2S(A)+2S(B)+2S(C)=S+4S().

Так как площади двуугольников

S(A)=2r 2 A, S(B)=2r 2 B, S(C)=2r 2 C,

то мы получим 4r 2 (A+B+C)=4r 2 +4S(), т.е. S()=r 2 (A+B+C)-r 2

Эта формула впервые была опубликована Альбертом Жираром в 1629г. [5].

Так как величины S() и r 2 положительны, то величина А+В+С- также положительна, откуда следует, что А+В+С, т.е. сумма углов сферического треугольника больше 180 градусов. Величина А+В+С- называется угловым или сферическим избытком данного сферического треугольника. Разность – величина положительная.

Таким образом, площадь сферического треугольника равна произведению его углового избытка на квадрат радиуса сферы.

Сумма всех сторон сферического треугольника всегда меньше .

Сумма углов сферического треугольника всегда меньше и больше .

6 . Тригонометрия сферического треугольника

Сферическая тригонометрия – математическая дисциплина, изучающая зависимости между углами и сторонами сферических треугольников.

Формулы сферической тригонометрии применяются для решения различных геодезических и астрономических задач.

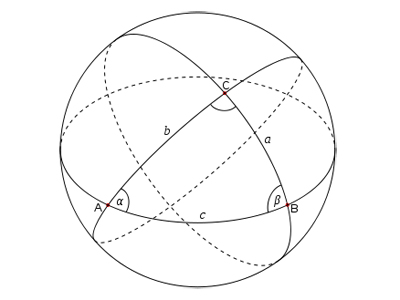
Пусть А, В, С - углы и а, b, с - противолежащие им стороны сферического треугольника ABC. Углы и стороны сферического треугольника связаны следующими основными формулами сферической тригонометрии:

Cos а = cos b cos с + sin b sin с cos А,

Cos A = - cos B cos С + sin B sin С cos a,

Sin a cos B = cos b sin c - sin b cos с cos А,

Sin А cos b = cos B sin C + sin B cos С cos a.

В этих формулах стороны а, b, с измеряются соответствующими центральными углами, длины этих сторон равны соответственно aR , bR , cR , где R — радиус сферы. Меняя обозначения углов (и сторон) по правилу круговой перестановки: А ® В ® С ® А ( а ® b ® с ® а ) , можно написать другие формулы сферической тригонометрии, аналогичные указанным. Формулы сферической тригонометрии позволяют по любым трём элементам сферического треугольника определить три остальные. [6].

7. Практическое применение геометрии сферического треугольника. В астрономии : 1. С помощью формулы площади сферического треугольника можно вычислить радиус планеты: R 2 = S () / (А+В+С-). Радиус является внутренней характеристикой планеты, поэтому определяется довольно сложно. Гораздо легче определить площадь конкретного планетарного сферического треугольника, измерить его углы и определить радиус.

2. Если расстояния до небесных объектов неизвестны, то в астрономии располагают их на поверхности сферы с центром в точке, где находится наблюдатель. Такая сфера называется небесной сферой . Радиус небесной сферы произволен, обычно его считают равным единице. С использованием небесной сферы в рамках космического проекта HIPPARCOS, осуществленного в 90-х годах XX века, измерили параллаксы (или расстояния) до 120 000 звезд, находящихся на расстоянии до 1 килопарсека от Солнца. Несмотря на то, что объем, в котором расположены эти звезды, составляет очень малую часть от объема нашей Галактики, измерение расстояний является важнейшим результатом проекта, потому что оказалось возможным построить трехмерную картину ближайшей окрестности Солнца.

Применение в мореплавании

С помощью теоремы косинусов для сферического треугольника, определеляют расстояние между двумя точками земной поверхности. Задача. Мореплаватель Америго Веспуччи проплыл 1800 миль в одном направлении из точки А к точке В, повернул на 60 градусов и проплыл в новом направлении еще 2700 миль, оказался в точке С. Требуется найти расстояние между точками А и С (по поверхности земного шара) (рис 15).

Решение: 1 морская миля равна 1 угловой минуте на земном меридиане, 1морская миля в 360·60 раз короче большой окружности земного шара, т.е. длина земного экватора равна 21600м.миль. 2pR=21600миль, R=21600/2p=10800/p.

Обозначим через a, b и с длины дуг ВС, АС и АВ соответственно,

 — внутренний угол при вершине В сферического треугольника АВС.

где R — радиус земного шара, выраженный в морских милях.

По теореме косинусов для сферического треугольника

Следовательно, длина дуги АС = b= R·0.90662 = 3437.4·0.906623116.7 миль.

Ответ: 3117 морских миль 5772 км.

Сферическая геометрия нужна не только астрономам, штурманам морских кораблей, самолетов, космических кораблей, которые по звездам определяют свои координаты, но и строителям шахт, метрополитенов, тоннелей, а также при геодезических съемках больших поверхностях Земли.

Применение в краеведении:

А теперь я расскажу о своих собственных исследованиях.

С помощью формул сферической тригонометрии можно расчитать дальность перелёта на зимовку птиц курского края.

Визитной карточкой курского края являются соловьи. Соловей считается одним из самых красивых певцов, пение соловья знают и любят многие. Самые лучшие певцы - "курские" соловьи. Поют только самцы, и главная роль песни - "обозначение" территории и привлечение самки. Соловей весит 20-30 грамм, питается преимущественно насекомыми, пауками и многоножками, то есть соловей является "защитником леса"!

Задача. Зимует "курский" соловей в Африке, южнее экватора (не севернее юга Эфиопии). Какое расстояние преодолевает соловей во время перелёта на зимовку?

Решение: Кратчайшее расстояние между двумя точками земной поверхности (если принять Землю за сферу) определяется формулой:

cos(d)= sin( φ А )·sin( φ B ) + cos( φ А )·cos( φ B )·cos( λ А − λ B ),

где φ А, φ B - координаты широты, λ А , λ B – координаты долготы данных пунктов (рис.16), d - расстояние между пунктами, измеряемое в радианах длиной дуги большого круга земного шара. Расстояние между пунктами, измеряемое в километрах, определяется по формуле: L =d·R, где R=6371км-средний радиус земного шара.

Зная географические координаты г. Курска и координаты Эфиопии, можно вычислить длину перелёта наших курских соловьёв в тёплые страны.

Координаты г. Курска: 51°43′00″ с. ш. 36°11′00″ в. д.

Координаты Эфиопии: 8°18′00″ с. ш. 39°07′00″ в. д.

cos(d)= sin(51°43′)·sin(8°18′) + cos(51°43′)·cos(8°18′)·cos(36°11′ −39°07′ )

d = arccos (0,7257)0,7592 радиан, L =d·R=0,7592·63714837км.

По этому алгоритму можно рассчитать длину пути, преодолеваемого перелётными птицами. В следующей таблицы приведены расстояния перелётов птиц Курской области.

Научно-исследовательские труды Бернхард Римана оказали огромное влияние на развитие математики в конце XIX и начале XX веков.

Уже в докторской диссертации Риманом были заложены основы геометрического направления теории аналитических функций. Выдающийся математик и геометр Риман ввел так называемые римановы поверхности, которые сыграли важную роль при исследовании многозначных функций. Более того, им была разработана теория конформных отображений, а также представлены основные идеи топологии, изучены условия существования аналитических функций внутри областей различного вида и многое другое.

Методы, разработанные Риманом нашли широкое применение в теории алгебраических функций и интегралов, по аналитической теории дифференциальных уравнений, в частности, уравнений, определяющих гипергеометрические функции, по аналитической теории чисел. К примеру, Риманом была указана связь распределения простых чисел со свойствами дзета-функции, а именно: с распределением её нулей в комплексной области — так называемая гипотеза Римана, однако ее справедливость ещё не доказана

Риманова геометрия — это раздел дифференциальной геометрии, объектом изучения которой, главным образом, являются римановы многообразия . Римановы многообразия — это гладкие многообразия с дополнительной структурой, римановой метрикой, то есть с выбором евклидовой метрики на каждом касательном пространстве, которая гладко меняется от точки к точке.

Подразделом римановой геометрии является геометрия в целом, которая выявляет связь глобальных свойств риманова многообразия (к примеру, топология или диаметр) и его локальных свойств (к примеру, ограничений на кривизну).

Основными элементами трехмерной римановой геометрии являются точки, прямые и плоскости.

В римановой геометрии имеют место такие предложения: через каждые две точки проходит одна прямая, каждые две плоскости пересекаются по одной прямой, каждые две прямые, лежащие в одной плоскости, пересекаются (в одной точке), точки на прямой расположены в циклическом порядке (как и прямые, лежащие в одной плоскости и проходящие через одну точку). Таким образом, требования аксиом римановой геометрии, относящиеся конгруэнтности, обеспечивают свободные движения фигур по плоскости и в пространстве Римана, как на плоскости, так и в пространстве Евклида.

Таким образом, Риман построил вторую разновидность неевклидовой геометрии в противоположность геометрии Лобачевского.

Уникальные идеи и методы, предложенные Риманом открыли новые пути для развития математики и нашли применение в механике и физике. Развитию римановой геометрии послужило создание итальянскими учеными Риччи-Курбастро и Леви-Чивита тензорного исчисления.

Создание аналитической геометрии Р.Декартом. Геометрии Лобачевского, Римана и их применение

Описание: Тема: Создание аналитической геометрии Р. Геометрии Лобачевского Римана и их применение. Создание аналитической геометрии Рене Декартом. Геометрии Лобачевского Римана и их применение: а геометрия Лобачевского; б создание неевклидовой геометрии; в утверждение геометрии Лобачевского; г геометрия Римана.

Дата добавления: 2015-01-27

Размер файла: 30.59 KB

Работу скачали: 16 чел.

Поделитесь работой в социальных сетях

Если эта работа Вам не подошла внизу страницы есть список похожих работ. Так же Вы можете воспользоваться кнопкой поиск

Тема: Создание аналитической геометрии Р.Декартом. Геометрии Лобачевского, Римана и их применение.

Создание аналитической геометрии Рене Декартом.
1. Геометрии Лобачевского, Римана и их применение:
а) геометрия Лобачевского;

б) создание неевклидовой геометрии;

в) утверждение геометрии Лобачевского;

г) геометрия Римана.

1.1. СОЗДАНИЕ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ РЕНЕ ДЕКАРТОМ.

Pене Декарт (1596-1650) (1596-1650) был выдающимся французским ученым: философом, физиком, математиком, физиологом. Образование он получил в иезуитском колледже, славившемся постановкой обучения. Всю жизнь Декарт продолжал совершенствоваться в науках. Целью естественнонаучных занятий Декарта была разработка общего дедуктивно-математического метода изучения всех вопросов естествознания. При этом Декарт совершенно отделил этот род своих занятий от метафизических рассуждений идеалистического характера. В границах физики Декарта единственную субстанцию, единственное основание бытия и познания представляет материя. Рационализм идей Декарта, признающего, прежде всего, разум, строгую дедукцию, был направлен против церковной схоластики. Природой материи, утверждал Декарт, является ее трехмерная объемность; важнейшими свойствами ее - делимость и подвижность. Эти же свойства материи должна отображать математика. Последняя не может быть либо численной, либо геометрической. Она должна быть универсальной наукой, в которую входит все, относящееся к порядку и мере. Все содержание математики должно рассматриваться с единых позиций, изучаться единым методом; само название науки должно отражать эту ее всеобщность. Декарт предложил назвать ее универсальной математикой.

Возникновение в первой половине XVII в. аналитической геометрии, установившей связь между алгеброй и геометрией, не было случайным. Оно было подготовлено как ходом развития математики до этого, так и общими потребностями производства, экономики, науки и торговли той эпохи.

Известно, что после Аполлония в Древней Греции не было крупных открытий в геометрии. В этой науке наступил длительный застой, причинами которого были не только политические и экономические условия, но и следующий существенный факт: геометрическая проблематика классического периода оказалась почти полностью исчерпанной. Все, что можно было сделать в геометрии с помощью ограниченного математического аппарата того времени, которым пользовались греки, было ими сделано, и сделанное вполне удовлетворяло запросам экономики, техники и науки.

Идеи Евдокса, Архимеда, Аполлония и других корифеев древней математики нельзя было развивать дальше без расширения понятия числа, введения в математику символики, идеи переменных величин и движения, без создания дифференциального и интегрального исчисления. Но такое революционное преобразование математики требовало не только длительного времени, но главным образом мощных внешних объективных факторов и стимулов, зависящих от производительных сил и производственных отношений. Лишь после великих географических открытий (Америки в 1492г., морского пути в Индию в 1498 г.), которые вызвали дальнейшее бурное развитие производства, торговли, мореплавания и поставили задачи составления географических карт, определения места корабля в море, составления более совершенных тригонометрических и астрономических таблиц и разработки более рациональных методов вычисления, лишь после возникновения в ряде европейских стран новой формы производства, стало заметным дальнейшее интенсивное развитие науки и техники. В трудах Галилея и других ученых была разработана новая механика, в которой нуждалось, впрочем, и военное дело, в частности баллистика, исследующая законы движения пуль и снарядов. Новое учение Коперника в астрономии привело к открытию Кеплером законов движения планет. Необходимость в более широких и точных наблюдениях небесных светил привела к построению целого ряда оптических инструментов и к развитию геометрической оптики. Все эти вопросы науки и техники поставили перед математикой ряд новых задач, неразрешимых старыми средствами и методами. Они-то и вызвали в XVII в. создание сначала аналитической геометрии, а затем дифференциального и интегрального исчисления. В основе аналитической геометрии, созданной Ферма и Р. Декартом, лежат две идеи: 1) идея координат, приведшая к арифметизации плоскости, т. е. к тому, что каждой точке плоскости ставится в соответствие два числа, взятые в определенном порядке, и наоборот, 2) идея истолкования любого уравнения с двумя неизвестными как некоторой линии на плоскости и, наоборот, представления любой линии, определяемой как некоторое геометрическое место точек, соответствующим уравнением.

Решение Декарта (устаревшее по форме и изложению и поэтому для нас довольно тяжелое) сводится к следующему. Он относит все линии к двум главным прямым: АВ, называемую х, и ВС. Последний отрезок он обозначает через у.

Прямая АВ выбирается как ось X , точка А − как начало координат. Ось Y по существу отсутствует, но подразумевается как направленная параллельно ВС. В целом система координат такая же, как и у Ферма. Для искомого геометрического места точки С Декарт после ряда выкладок получает уравнение:

Это уравнение второго порядка, представляющее коническое сечение, в котором каждая буква означает некоторый отрезок (расстояние). Уравнение (1) представляет, по Декарту, длину отрезка ВС, если АВ или х берется неопределенным (т. е. как переменная). Далее Декарт занимается вопросом о том, какое именно коническое сечение изображает уравнение (1) при тех или иных значениях постоянных (коэффициент), входящих в него. Если радикал в правой части (1) равен нулю, пишет Декарт, то точка С описывает прямую . И в случае, если этот корень извлекается, искомое место будет некоторой прямой.

Аналитическая геометрия в трудах Эйлера, у его современников и последователей. Большая часть математических работ Л. Эйлера относится, как известно, к области математического анализа. Тем не менее, он посвятил более 75 трудов геометрии и разным ее применениям. Он получил важнейшие результаты в теории алгебраических кривых и в дифференциальной геометрии и положил начало топологии, учению о симметрии и о других геометрических преобразованиях.

В последней четверти XIX столетия начался следующий важнейший этап в развитии аналитической геометрии как науки: введение в нее учения о геометрических преобразованиях и теории инвариантов. Аналитическая геометрия имела большое значение для развития дифференциальной геометрии, проективной геометрии, аналитической механики и других разделов математики и физики. Она и в настоящее время необходима для изучения математики и естествознания. Исходя из двумерной и трехмерной, развилась многомерная и бесконечномерная аналитическая геометрия . В известной мере продолжение идей классической аналитической геометрии отражено в современном функциональном анализе, обобщающем понятия математического анализа, и в общей алгебраической геометрии, связанной с теорией функций и с топологией.

1.2. ГЕОМЕТРИИ ЛОБАЧЕВСКОГО, РИМАНА И ИХ ПРИМЕНЕНИЕ.

Геометрия Лобачевского (гиперболическая геометрия) − одна из неевклидовых геометрий, геометрическая теория, основанная на тех же основных посылках, что и обычная евклидова геометрия, за исключением аксиомы о параллельных, которая заменяется на аксиому о параллельных Лобачевского.

Попытки доказательства пятого постулата

Среди многих пытавшихся доказать пятый постулат были, в частности, следующие крупные учёные.

Древнегреческие математики Птолемей ( II в.) и Прокл ( V в.) (основывался на предположении о конечности расстояния между двумя параллельными).

Ибн аль-Хайсам из Ирака (конец X начало XI вв.) (основывался на предположении, что конец движущегося перпендикуляра к прямой описывает прямую линию).

Иранские математики Омар Хайям (2-я половина XI начало XII вв.) и Насир ад-Дин ат-Туси ( XIII в.) (основывались на предположении, что две сходящиеся прямые не могут при продолжении стать расходящимися без пересечения).

Первую в Европе известную нам попытку доказательства аксиомы параллельности Евклида предложил живший в Провансе (Франция) Герсонид (он же Леви бен Гершом, XIV век). Его доказательство опиралось на утверждение о существовании прямоугольника.

Катальди (впервые в 1603 году напечатал работу, целиком посвященную вопросу о параллельных).

Английский математик Валлис (1663, опубликовано в 1693) (основывался на предположении, что для всякой фигуры существует ей подобная, но не равная фигура).

Французский математик Лежандр (1800) (основывался на допущении, что через каждую точку внутри острого угла можно провести прямую, пересекающую обе стороны угла; у него также были другие попытки доказательства).

При этих попытках доказательства пятого постулата математики вводили (явно или неявно) некоторое новое утверждение, казавшееся им более очевидным.

Были предприняты попытки использовать доказательство от противного: итальянский математик Саккери (1733) (сформулировав противоречащее постулату утверждение, он вывел ряд следствий и, ошибочно признав часть из них противоречивыми, он счёл постулат доказанным). Немецкий математик Ламберт (около 1766, опубликовано в 1786) (проведя исследования, он признал, что не смог обнаружить в построенной им системе противоречия).

Наконец, стало возникать понимание о том, что возможно построение теории, основанной на противоположном постулате: немецкие математики Швейкарт (1818) и Тауринус (1825) (однако они не осознали, что такая теория будет логически столь же стройной).

Создание неевклидовой геометрии

Одновременно и независимо к аналогичным выводам пришёл Янош Бойяи, а Карл Фридрих Гаусс пришёл к таким выводам ещё раньше. Однако труды Бойяи не привлекли внимания, и он вскоре оставил эту тему, а Гаусс вообще воздерживался от публикаций, и о его взглядах можно судить лишь по нескольким письмам и дневниковым записям. Например, в письме 1846 года астроному Г. X . Шумахеру Гаусс так отозвался о работе Лобачевского:

Это сочинение содержит в себе основания той геометрии, которая должна была бы иметь место и притом составляла бы строго последовательное целое, если бы евклидова геометрия не была бы истинной…

В итоге Лобачевский выступил как первый наиболее яркий и последовательный пропагандист этой теории.

Утверждение геометрии Лобачевского

Лобачевский умер в 1856 году. Спустя несколько лет была опубликована переписка Гаусса, в том числе несколько восторженных отзывов о геометрии Лобачевского, и это привлекло внимание к трудам Лобачевского. Появляются переводы их на французский и итальянский языки, комментарии видных геометров. Публикуется и труд Бойяи.

В 1868 году выходит статья Э. Бельтрами об интерпретациях геометрии Лобачевского. Бельтрами определил метрику плоскости Лобачевского и доказал, что она имеет всюду постоянную отрицательную кривизну. Такая поверхность тогда уже была известна − это псевдосфера Миндинга. Бельтрами сделал вывод, что локально плоскость Лобачевского изометрична участку псевдосферы. Окончательно непротиворечивость геометрии Лобачевского была доказана в 1871 году, после появления, модели Клейна.

Вейерштрасс посвящает геометрии Лобачевского специальный семинар в Берлинском университете (1870). Казанское физико-математическое общество организует издание полного собрания сочинений Лобачевского, а в 1893 году столетие русского математика отмечается в международном масштабе.

Геометрия Римана - многомерное обобщение геометрии на поверхности, представляющее собой теорию римановых пространств, т. е. таких пространств, где в малых областях приближённо имеет место евклидова геометрия (с точностью до малых высшего порядка сравнительно с размерами области). Риманова геометрия получила своё название по имени Б.Римана, который заложил её основы в 1854 г.

Простейший пример риманова пространства представляет любая гладкая поверхность. Действительно, в достаточно малой окрестности любой точки она совпадает (с точностью до величин высшего порядка малости) с касательной плоскостью в этой точке; поэтому в такой окрестности соотношения длин на поверхности будут такими же, как на плоскости (конечно, с точностью до малых величин высшего порядка). Таким образом, в малых областях поверхности имеет место (с точностью до малых величин высшего порядка) евклидова геометрия.

Например, при измерениях на участках земной поверхности, малых в сравнении с размерами земного шара, можно с успехом применять обычную планиметрию. Однако результаты измерений на больших участках обнаруживают существенное отклонение от законов планиметрии.

Таким образом, поверхность, рассматриваемая с точки зрения измерений, проводимых на ней, оказывается двумерным пространством, геометрия которого (т. н. внутренняя геометрия поверхности), будучи евклидовой в бесконечно малом, в целом не является евклидовой; к тому же, как правило, такое пространство неоднородно по своим геометрическим свойствам. Внутренняя геометрия поверхности есть не что иное, как риманова геометрия в случае двух измерений, а поверхность, рассматриваемая с точки зрения её внутренней геометрии, есть двумерное риманово пространство.

Перенесение этих понятий на многомерные пространства приводит к общей римановой геометрии. Именно, рассматривается абстрактное пространство n измерении, в котором задаётся закон измерения расстояний, совпадающий вблизи каждой точки с обычным евклидовым с точностью до бесконечно малых высшего порядка.

В основе рассматриваемой геометрии лежат три идеи.

Первая идея - признание того, что вообще возможна геометрия, отличная от евклидовой, была впервые развита Н.И.Лобачевским.

Вторая - это идущее от К.Гаусса понятие внутренней геометрии поверхностей и её аналитический аппарат в виде квадратичной формы, определяющий линейный элемент поверхности.

Третья идея - это понятие об n-мерном пространстве, выдвинутое и разработанное в простейших случаях в 1-й половине 19 в. рядом геометров.

Б.Риман, соединив и обобщив эти идеи, ввёл, во-первых, общее понятие о пространстве как о непрерывной совокупности любого рода однотипных объектов, которые служат точками этого пространства. Во-вторых, Б.Риман перенёс на эти абстрактные пространства представление об измерении длин бесконечно малыми шагами, т. е. дал общее понятие о метрике, определяемой формулой ds = f ( x 1, x 2, . xn ; dx 1, dx 2, . dxn ).

Риманова геометрия, многомерное обобщение геометрии на поверхности, представляющее собой теорию римановых пространств, т. е. таких пространств, где в малых областях приближённо имеет место евклидова геометрия (с точностью до малых высшего порядка сравнительно с размерами области). Риманова геометрия получила своё название по имени Б. Римана, который заложил её основы в 1854.

Гладкая поверхность в евклидовом пространстве, рассматриваемая с точки зрения измерений, производимых на ней, оказывается двумерным пространством, геометрия которого (так называемая внутренняя геометрия), будучи приближённо евклидовой в малом (в окрестности любой точки она совпадает с точностью до малых высшего порядка с геометрией касательной плоскости), точно не является евклидовой; к тому же, как правило, поверхность неоднородна по своим геометрическим свойствам. Поэтому внутренняя геометрия поверхности и есть не что иное, как Риманова геометрия двух измерений, а сама поверхность есть двумерное риманово пространство.

Так, при измерениях на участках земной поверхности, малых в сравнении с размерами земного шара, можно с успехом применять обычную планиметрию, однако результаты измерений на больших участках обнаруживают существенное отклонение от законов планиметрии. Перенесение этих понятий на многомерные пространства приводит к общей Риманова геометрия

После опубликования работ Римана его идеи привлекли внимание ряда математиков, которые развивали дальше аналитический аппарат Риманова геометрия и устанавливали в ней новые теоремы геометрического содержания. Важным шагом было создание итальянскими геометрами Г. Риччи-Курбастро и Т. Леви-Чивита на рубеже 20 в. так называемого тензорного исчисления, которое оказалось наиболее подходящим аналитическим аппаратом для разработки Риманова геометрия Решающее значение имело применение Риманова геометрия в создании А. Эйнштейном общей теории относительности, которое было триумфом не только абстрактной геометрии, но и идей о связи геометрии и физики, выдвинутых Лобачевским и Риманом. Это привело к бурному развитию Риманова геометрия и её разнообразных обобщений. В настоящее время Риманова геометрия вместе с её обобщениями представляет собой обширную область геометрии, которая продолжает успешно развиваться, причём особое внимание уделяется вопросам глобального характера.

… Его работа по геометрии оказала чрезвычайно большое влияние на развитие математических и физических идей. Дело в том, что Риман дал классификацию всех существующих видов геометрии, включая найденные уже неевклидовы геометрии, и показал возможность создания любого числа новых пространств. Эта работа открыла Эйнштейну путь к разработке общей теории относительности.

Георг Фридрих Бернхард Риман (17 сентября 1826 – 20 июля 1866) – знаменитый немецкий математик, известный своими работами по теории функций и новаторскими теориями в области дифференциальной геометрии. Пути развития современной математики в значительной мере были предопределены трудами этого ученого.

Риман родился в семье бедного пастора, вторым из шести его детей, в деревне Брезеленц, недалеко от Данненберга. Школу смог начать посещать лишь с 14 лет. Мать Римана, Шарлотта Эбелль, умерла от туберкулёза, когда он ещё учился в школе; от этой же болезни умерли две его сестры.

Наклонности к математике проявлялись у молодого Римана ещё в детстве, но, уступая желанию отца, Риман поступил в 1846 году в Гёттингенский университет для изучения филологии и богословия. Однако здесь он слушает лекции Гаусса и принимает окончательное решение стать математиком.

В 1847 году Бернхард Риман переходит в Берлинский университет, где слушает лекции Дирихле, Якоби и Штейнера. В 1849 году он возвращается в Гёттинген. Там Риман знакомится с Вильгельмом Вебером, который становится его учителем и близким другом. Годом позже приобретает ещё одного друга – Рихарда Дедекинда.

С 1854 года Бернхард Риман работает в Гёттингенском университете. За следующие 10 лет он преобразовал сразу несколько разделов математики.

В этом знаменитом докладе Риман определил общее понятие n -мерного многообразия и его метрику в виде произвольной положительно определённой квадратичной формы. Далее Риман обобщил гауссову теорию поверхностей на многомерный случай; при этом был впервые введён тензор кривизны и другие понятия римановой геометрии. Существование метрики, по Риману, объясняется либо дискретностью пространства, либо некими физическими силами связи – здесь он предвосхитил общую теорию относительности. Альберт Эйнштейн писал:

Риман первый распространил цепь рассуждений Гаусса на континуумы произвольного числа измерений, он пророчески предвидел физическое значение этого обобщения евклидовой геометрии.

Риман также высказал предположение, что геометрия в микромире может отличаться от трёхмерной евклидовой геометрии:

Эмпирические понятия, на которых основывается установление пространственных метрических отношений, – понятия твёрдого тела и светового луча, по-видимому, теряют всякую определённость в бесконечно малом. Поэтому вполне мыслимо, что метрические отношения пространства в бесконечно малом не отвечают геометрическим допущениям; мы действительно должны были бы принять это положение, если бы с его помощью более просто были объяснены наблюдаемые явления.

Риман является создателем геометрического направления теории аналитических функций. Он ввёл носящие его имя поверхности (римановы поверхности) и разработал теорию конформных отображений.

Всё же Бернхард Риман был принят приват-доцентом Гёттингенского университета, где читает курс абелевых функций. На его первую лекцию, говорят, пришло всего лишь восемь человек, а на следующую и того меньше. Дело в том, что Риман ощущал сначала известные трудности при чтении лекций. Но спустя некоторое время он писал:

Моя первоначальная застенчивость уже несколько прошла: я привыкаю больше думать о слушателях, чем о себе, и научился читать по их лицам, могу ли продолжать лекцию или должен еще раз вернуться к рассматриваемой проблеме…

Застенчивость Римана вскоре совершенно прошла, и, благодаря его тщательной подготовке к лекциям, он стал добиваться хороших результатов в обучении студентов. В своих лекциях он использовал часто нигде не опубликованные материалы.

В 1857 году Риман публикует классические труды по теории абелевых функций и аналитической теории дифференциальных уравнений.

Вслед за Коши, Риман рассмотрел формализацию понятия интеграла и ввёл своё определение – интеграл Римана. Развил общую теорию тригонометрических рядов, не сводящихся к рядам Фурье.

Исследование Риманом распределения простых чисел имело большой резонанс. Он дал интегральное представление дзета-функции (ζ-функция Римана)

ζ(s) = 1 –s + 2 –s + 3 –s + . ,

исследовал её полюса и нули, вывел приближённую формулу для оценки количества простых чисел через интегральный логарифм.

Исследования Римана в области механики относятся к изучению динамики течений сжимаемой жидкости (газа) – в частности, сверхзвуковых. Риман стал одним из основоположников классической газовой динамики. Именно ему механика обязана понятием об ударных волнах. Явление образования ударных волн в потоке сжимаемого газа впервые было обнаружено не экспериментально, а теоретически – в ходе проводившегося Риманом изучения решений уравнений движения газа.

В последние годы своей недолгой жизни Риман был удостоен многочисленных почестей, получил признание ведущих ученых, был избран членом различных научных обществ, в том числе Лондонского Королевского общества и Французской Академии наук.

Последние четыре года жизни учёный провел в Италии.

20 июля 1866 года Риман скончался от туберкулёза в возрасте 39 лет.

Дедекинд, со слов жены, так описал его смерть:

Могила Римана в Италии была заброшена и позже уничтожена при перепланировке кладбища, но надгробная плита уцелела и в наши дни установлена у стены кладбища.

Посмертный сборник трудов Римана, подготовленный Дедекиндом, содержал всего один том. После смерти учёного слушатели его лекций тщательно собрали свои записи, и таким образом было создано дополнение к собранию трудов Римана, изданное почти через сорок лет после его смерти.

Некоторые математические идеи Римана вошли в науку, и носят имя автора. Не каждому ученому выпала такая честь. Даже очень далекие от математики люди слышали о так называемом Римановом пространстве. Предложенные великим математиком Бернхардом Риманом идеи и методы раскрыли новые пути в развитии математики, и нашли применение в механике и физике. И, несмотря на то, что он написал немного работ, а напечатал еще меньше, любая из них отличалась огромной важностью и множеством новых идей.

Некоторое понятие о том, как много сделал Риман для развития математики, может дать перечень математических объектов, носящих его имя:
- гипотеза Римана:
- обобщенная гипотеза Римана
- большая гипотеза Римана
- гипотеза Римана для кривых над конечными полями
- дзета-функция Римана
- инварианты Римана
- интеграл Римана
- кратный интеграл Римана
- обобщенный интеграл Римана
- интеграл Римана – Стилтьеса
- производная Римана
- риманова кривизна
- риманова геометрия (многомерное обобщение геометрии)
- геометрия Римана (эллиптическая геометрия)
- риманова поверхность
- риманово пространство
- сфера Римана
- сферическая геометрия Римана
- соответствие Римана – Гильберта
- тензор Римана
- теорема Римана из теории конформных отображений
- теорема Римана об условно сходящихся рядах
- теорема Римана об устранимой особой точке
- теорема Римана – Роха
- условия Коши – Римана
- инвариант Римана
- леммы Римана-Лебега
- матрица Римана
- формулы Римана – Зигеля
- тета-функции Римана – Зигеля
- вектор Римана – Зильберштейна
- сумма Римана
- псевдориманово многообразие
- риманова связность
- риманова связность на поверхности.
Читайте также: