Проверка динамических рядов на автокорреляцию реферат

Обновлено: 04.07.2024

Автокорреляция в динамических рядах – зависимость между уровнями ряда или зависимость между исходным динамическим рядом и тем же рядом, но смещенным на определенный временной интервал, называемый лагом.

Лаг – временной интервал, разделяющий зависимые уровни.

Исходный Смещенные ряды

Наличие автокорреляции в рядах динамики оценивается на основе коэффициентов автокорреляции, которые строятся и рассчитываются аналогично коэффициентам парной корреляции

– уровни исходного ряда

– уровни смещенного ряда

i – временной лаг

– среднеквадратическое отклонение, рассчитанное на основе значений исходного ряда

- среднеквадратическое отклонение, рассчитанное на основе значений смещенного ряда

Величина лага определяет порядок коэффициента:

если lag = 1, то говорят о коэффициенте автокорреляции первого порядка

если lag = 2, то говорят о коэффициенте автокорреляции второго порядка

Если n > 20 и рассчитывается коэффициент автокорреляции первого порядка, то , .

Чем больше величина лага и чем меньше число уровней в изучаемом ряду, тем больше разница в значениях средних уровней и стандартных отклонений коррелируемых рядов.

Коэффициент автокорреляции, как и парный коэффициент, изменяется в пределах от -1 до 1.

Оценка существенности (статистической значимости коэффициента автокорреляции) осуществляется на основе t- статистики:

t_ф ≥ t_т - чтобы признать величину коэффициента автокорреляции статистически значимой.

Близость коэффициента автокорреляции к нулю будет свидетельствовать об отсутствии автокорреляции в уровнях рядов, к единице – о присутствии.

Наличие автокорреляции в рядах динамики (что характерно для экономических и социальных явлений) свидетельствует о присутствии тенденции в изучаемых рядах.

Если исследуемый временной ряд включает достаточное число временных рядов, то могут быть рассчитаны коэффициенты автокорреляции высоких порядков.

Последовательность коэффициентов автокорреляции r_a₁, r_a₂, r_a₃, … , r_ai принято называть автокорреляционной функцией. На ее основе может быть изучена внутренняя структура динамического ряда, то есть можно получить ответы на вопросы: присутствует ли тенденция в изучаемом ряду, подвержены ли уровни ряда циклическим (сезонным) колебаниям; и указать период циклических колебаний, о котором свидетельствуют максимальные значения коэффициентов автокорреляции.

На основе функции автокорреляции строится график, который называется коррелограмма.

Высокое значение автокорреляции первого порядка свидетельствует о присутствии тенденции в изучаемом ряду. Высокие значения 4, 8 и 12 порядков корреляции говорят о присутствии циклических колебаний в динамике инвестиций в основной капитал, период цикла – четыре квартала. Однако величине коэффициента автокорреляции 12 порядка вряд ли стоит доверять, так как он рассчитан на основе четырех коррелируемых пар показателей.

Если установлено наличие автокорреляции в уровнях ряда, то тенденция изучаемого временного ряда может быть описана на основе уравнения авторегрессии.

Уравнение тренда: y = a + bt

Уравнение авторегрессии: y = a + by_t_-_i (в качестве фактора выступает предшествующий уровень).

Выбор уравнения авторегрессии осуществляется по аналогии с уравнением тренда и оценка его качества – по тем же критериям.

Величина i определяется исходя из порядка коэффициента автокорреляции, имеющего максимальное значение (если величина коэффициента статистически значима).

Если в изучаемом временном ряду отсутствуют циклические колебания, то коррелограмма отразит затухающую автокорреляционную функцию, так как чем выше порядок автокорреляции, тем меньше будет его значение. Поэтому в динамических рядах, построенных по данным годичных интервалов, как правило, максимальное значение имеет коэффициент автокорреляции первого порядка. Строится уравнение, в котором фактором выступает ряд, смещенный на один лаг.

Если получено удовлетворительное уравнение авторегрессии, на его основе может быть осуществлен прогноз, но следует помнить, что чем больше период упреждения, тем менее точен прогноз (так как уже на втором шаге прогноза в качестве фактора в уравнение подставляется уже спрогнозированная величина).

На практике часто возникает необходимость изучения связей между двумя или несколькими динамическими рядами. Статистическим процедурам анализа всегда должен предшествовать теоретический анализ на основе положений экономической теории и знаний о тех процессах и явлениях, которые описываются имеющимися динамическими рядами. Этот анализ необходим чтобы избежать оценки так называемой ложной корреляции при реальном отсутствии зависимости между явлениями.

Если в изучаемых рядах существуют однонаправленные тенденции, то коэффициент корреляции получается завышенным. Если в изучаемых рядах присутствуют разнонаправленные тенденции, то значения коэффициентов корреляции получаются заниженными. Поэтому, если теоретически обоснованно наличие связи между временными рядами, то при статистической ее оценке следует исключить также с невыполнением одного из условий применения метода корреляционно-регрессионного анализа.

В динамических рядах, как правило, присутствует автокорреляция уровней, что говорит о невыполнении условия независимости наблюдений.

Статистикой разработано несколько вариантов исключения тенденции из временных рядов.

I В первую очередь возможно коррелировать не уровни рядов, а остатки от трендовых моделей. При этом выполняются следующие шаги:

1) строятся статистически значимые трендовые модели для каждого ряда;

2) определяются остатки от трендовых моделей;

3) оценивается наличие автокорреляции в остатках. Если в остатках автокорреляция присутствует, то опять строится модель и заново вычисляются остатки. Если в остатках автокорреляция присутствует, то на основе значений остатков рассчитывают показатели корреляции и строят модель.

II Коррелирование показателей, являющихся постоянными в трендовых моделях. Так, в условиях линейного тренда коррелируются цепные абсолютные приросты. Если тренд описывался экспонентой, коррелируются цепные коэффициенты роста. Если тренды в изучаемых рядах описаны с использованием разных функций, возможно коррелировать разные показатели.

III Переход от парной регрессии ко множественной регрессии путем прямого включения в уравнение связи фактора времени.

Математической статистикой доказано, что включение фактора времени аналогично коррелированию остатков от трендовых моделей.

Самый распространенный вариант ухода от автокорреляции.

При изучении зависимости между временными рядами следует учитывать возможность запаздывания изменения уровней другого временного ряда. При коррелировании таких рядов следует учитывать этот временной лаг.

Многие экономические процессы растянуты по времени и требуют анализа данных за ряд лет. В экономике для этой цели используются модели временных рядов, то есть, модели, которые строятся по данным, которые отражают изменение какого-либо процесса или объекта за ряд лет.
Модели временных рядов анализируются методами корреляционно-регрессионного анализа, который позволяет выявить наличие зависимости между переменными, строить прогноз и т.д. Однако, не всегда имеющиеся данные подходят для построения модели временных рядов, поскольку во временных рядах могут встречаться определенные колебания – такова особенность временных рядов.
Так, например, в данных могут содержаться сезонные или циклические колебания, которые могут искажать конечный результат корреляционно-регрессионного анализа. Для получения корректного результата сезонную или циклическую компоненту нужно исключить из временного ряда.
В некоторых данных может содержаться ложная корреляция, которая также приводит к некорректным результатам. Эта корреляция носит название автокорреляции.
Таким образом, исследование методов обнаружения и устранения автокорреляции в моделях авторегрессии представляется актуальным.
Целью работы является изучение теоретических и методологических аспектов выявления и устранения автокорреляции и авторегрессии в рядах динамики.
Для достижения поставленной цели необходимо решить ряд задач:
определить сущность автокорреляции и авторегрессии, выявить их причины;
выявить последствия проявления автокорреляции и авторегрессии;
исследовать методы выявления и устранения автокорреляции и авторегрессии.

1 Теоретические аспекты автокорреляции и авторегрессии в рядах динамики
1.1 Определения, причины автокорреляции и авторегрессии,
авторегрессионная функция
Автокорреляция представляет собой взаимозависимость элементов временного или пространственного ряда. Причем стоит отметить, что эти элементы должны быть последовательны, то есть, идти друг за другом. Также существует такое явление, как автокорреляция остатков – то есть, наличие постоянной дисперсии остатков при значительной ковариации.
Чаще всего такое явление наблюдается во временных рядах. Как уже упоминалось ранее, так может проявляться специфика временного ряда. Однако, иногда наличие автокорреляции обусловлено ошибкой в спецификации эконометрической модели. Также это может говорить о том, что в модель нужно внести новую переменную с независимыми характеристиками.
Наличие автокорреляции противоречит одному из требований метода наименьших квадратов (далее – МНК) – требования о том, чтобы остатки, полученные в результате решения уравнения регрессии, были случайными.
Авторегрессия – это процесс, который позволяет определять значения показателей будущих периодов на основе значений показателей прежних периодов. Таким образом, в основе данного процесса лежит предположение о том, что предыдущие значения определенного показателя могут влиять на его последующие значения. Авторегрессия AR (1) – это процесс первого уровня, при котором будущее значение показателя вычисляется из предыдущего значения. Например, выручка предприятия за текущий 2019 год определяется, исходя из значений выручки предприятия за предыдущий 2018 год. Авторегрессия AR (2) – это процесс второго уровня, при котором будущее значение показателя вычисляется из двух предыдущих значений, идущих подряд. Например, выручка предприятия за текущий 2019 год определяется, исходя из значений выручки предприятия за предыдущие два года – 2017-2018 годы.
Основными причинами, приводящими к автокорреляции, являются следующие:
1) Ошибки спецификации проявляются тогда, когда в модели не учитывается какой-то важный параметр переменной. Также такие ошибки проявляются, если неверно выбрана форма корреляции. В обоих случаях наблюдается отклонение точек наблюдения от линии регрессии, что влечет за собой проявление автокорреляции и некорректные результаты.
2) Инерция. Многие экономические показатели (например, инфляция, безработица, ВНП и т.п.) возникают циклично

Зарегистрируйся, чтобы продолжить изучение работы

1.2 Последствия автокорреляции и авторегрессии в рядах динамики и
методы избавления
Автокорреляция в моделях авторегрессии приводит к неверным результатам при вычислении средних квадратических ошибок коэффициентов регрессии. Автокорреляция также не позволяет построить достоверные доверительные интервалы, проверить их соответствие определенным требованиям. наличие автокорреляции также может привести к уменьшению числа наблюдений, что тоже искажает результаты.
Среди последствий также можно выделить следующие:
оценки параметров, оставаясь линейными и несмещенными, перестают быть эффективными;
дисперсии оценок являются смещенными, что может привести к признанию статистически значимыми объясняющие переменные, которые в действительности таковыми могут и не являться.
Кроме того, оценка дисперсии регрессии (формула 1.8) является смещенной оценкой истинного значения , во многих случаях занижая его:
(1.8)
Выводы по t- и F-статистикам, определяющим значимость коэффициентов регрессии и коэффициента детерминации, могут иметь неверное значение. Вследствие этого ухудшаются прогнозные качества модели.
В этом случае можно воспользоваться методами, которые позволяют устранить автокорреляцию.
1) Определение р на основе статистики Дарбина-Уотсона. Этот метод наиболее эффективен, когда имеется большое количество наблюдений. В этом случае оценка параметра p будет достаточно точной.
Взаимосвязь между статистикой Дарбина-Уотсона и параметром авторегрессии определяется выражением:
(1.9)
Тогда в качестве оценки p можно принять:
(1.10)
где (1.11)
2) Метод Кохрана-Оркатта. Это итерационная процедура. Алгоритм таков. Сначала необходимо оценить исходную регрессию:
(1.12)
Затем необходимо определить остатки:
, (1.13)
В качестве первого приближения параметра p следует взять его МНК-оценку в регрессии (это уравнение не содержит константу).:
(1.14)
Далее нужно оценить полученную регрессию:
(1.15)
Снова определяются остатки

(временные ряды) или в пространстве (пространственные данные).

Среди основных причин, вызывающих появление автокорреляции,

Ошибки спецификации . Отсутствие учета в модели какой-либо важной

объясняющей переменной либо неправильный выбор формы зависимости,

обычно приводит к системным отклонениям точек наблюдений от линии

Инерция. Многие экономические показатели (например, инфляция,

безработица, ВНП и т. п.) обладают определенной цикличностью, связанной

Действительно, экономический подъем приводит к росту занятости,

сокращению и нфляции, увеличению ВНП и т.д. Этот рост продолжается до

тех пор, пока изменение конъюнктуры рынка и ряда экономических

характеристик не приведет к замедлению роста, затем остановке и движению

вспять рассматриваемых показателей. В любом случае эта трансформ ация

происходит не мгновенно, а обладает определенной инертностью.

Эффект паутины. Во многих производств енных и других с ферах

экономические показатели реагируют на изменение экономических условий с

запаздыванием (временным лаг ом). Например, предложение

сельскохозяйственной продукции реагирует на изменение цены с

запаздыванием (равным периоду созревания урожая). Большая цена

сельскохозяйственной продукции в прошедшем году вызовет (скорее всего)

ее перепроизводство в текущем году, а, следовательно, цена на эту

продолжительному временному периоду получают усреднением данных по

составляющим его подынтервалам. Это может привести к определенному

сглаживанию колебаний, которые имелись внутри рассматриваемого

периода, что в свою очередь может послужить причиной автокорреляции.

Обычно эконометрические модели строятся на основе двух типов исходных

 данные, характеризующие совокупность различных объектов в

 данные, характеризующие один объект за ряд последовательных

Модели, построенные по данным первого типа, называются

пространственными моделями. Модели, построенные на основе второго

Временной ряд – совокупность значений какого-либо показателя за

несколько последовательных моментов или периодов времени. Каждый

уровень временного ряда формируется под воздействием большого числа

факторов, которые условно можно подразделить на три группы:

 факторы, формирующие тенденцию ряда (например, инфляция влияет

 факторы, формирующие циклические колебания ряда (например,

уровень безработицы в курортных городах в зимний период выше по

Очевидно, что реальные данные чаще всего содержат все три компоненты.

Модель, в которой временной ряд представлен как сумма перечисленных

компонент, называется аддитивной моделью временного ряда. Если же

временной ряд представлен как их произведение, то такая модель называется

Под временным рядом (time series) поним ается последовательность

наблюдений значений некоторой переменной, произведенных через равные

промежутки времени. Если принять длину такого промежутка за единицу

времени (год, квартал, день и т.п.), то можно считать, что последовательные

Основная отличительная особенность статистического анализа временных

рядов состоит в том, что последовательность наблюдений

x1, . xn рассматривается как реализация последовательности , вообще

говоря, статистически зависимых случайных величин X1, . Xn , имеющих

некоторое совместное распределение с ф ункцией распределения

распределение случайных величин X1, . Xn имеет совместную плотность

Чтобы сделать задачу статистического анализа временных рядов доступной

для практического решения, приходится так или иначе ограничивать класс

рассматриваемых моделей временных рядов , вводя те или иные

предположения относительно структуры ряда и структуры его

вероятностных характеристик. Одно из таких ограничений предполагает

Ряд xt , t = 1, …, n , называется строго стационарным (или стационарным в

вероятностей случайных величин X t1…… X tm такое же, как и для X

t1+ш…… X tm + I , при любых t1,…, tm и I, таких , что 1 ≤ t1, … , tm ≤ n и 1

Другими словами, свойства строго стационарного врем енного ряда не

изменяются при изменении начала отсчета времени . В частности, при m = 1

из предположения о строгой стационарности временного ряда xt следует, что

закон распределения вероятностей случайной величины Xt не зависит от t, а

значит, не зависят от t и все его основные числовые характеристики (если,

конечно, они существуют), в том числе: м атематическое ожидание E (Xt) =

Значение М. определяет постоянный уровень, относительно которого

колеблется анализируемый временной ряд xt, а постоянная Ớ

Одно из главных отличий последовательности наблюдений,образующих

временной ряд, заключается в том, что члены временного ряда являются,

вообще говоря, статистически взаимозависимыми . Степень тесноты

статистической связи между случайными величинами Xt и Xt+ может

Если ряд xt стационарный, то значение не зависит от t и

является функцией только от ; мы будем использовать для него

Соответственно, для стационарного ряда и значение коэффициента

зависит только от ; мы будем использовать для него обозначение

Практическая проверка строгой стационарности ряда xt на основании

наблюдения значений x1, x2, …, xn в общем случае затруднительна . В связи с

Еще одним подходом к описанию основной тенденции временного ряда и прогнозированию является авторегрессионная модель. Ее построению предшествует оценка наличия автокорреляции в изучаемом ряду.

При анализе динамических рядов особый интерес представляет оценка степени зависимости изменений в уровнях одного ряда от изменений, происходящих в уровнях другого ряда

Вторая особенность состоит в том, что одним из основных условий применения методов корреляции является независимость отдельных наблюдений.

Автокорреляция – это зависимость между последовательными значениями (уровнями) временного ряда. Автокорреляция первого порядка (first-order autocorrelation) оценивает степень зависимости между соседними значениями временного ряда. Автокорреляция второго порядка (second-order autocorrelation) оценивает тесноту связи между значениями, разделенными двумя временными интервалами, и т.д. Интервал времени, разделяющий зависимые уровни динамического ряда, называется лагом (lag). Автокорреляционная зависимость может быть представлена как зависимость между уровнями исходного ряда:

у1, у2, у3, … , уn

и того же ряда, но смещенного на i периодов (моментов) времени:

, у2-i, у3-i, … , уn-i.

Интервал смещения (i) - временной лаг (i = 1, i = 2, i = 3 и т. д.).

Если при изучении отдельных динамических рядов наличие автокорреляции помогало выявлению тенденции развития явления, то при анализе корреляционной зависимости между рядами ее следует исключить.

Наличие автокорреляции проверяется на основе коэффициентов автокорреляции. При этом в качестве результативного признака принимается переменная, содержащая фактические значения уровней исходного ряда динамики, а в качестве факторного признака переменная, содержащая фактические уровни смещенного ряда. Величина временного лага определяет порядок коэффициента автокорреляции.

Математической статистикой разработаны циклический и нециклический коэффициент автокорреляции. На практике чаще используется нециклический коэффициент автокорреляции, который может быть рассчитан по формуле:

Если динамический ряд У(t) достаточно большой, а i = 1, то дисперсии рядов У(t), У(t-i), а также их средние уровни практически равны. Поэтому формулу можно записать следующим образом:

Для проверки нулевой гипотезы об отсутствии автокорреляции фактическая величина коэффициента сопоставляется с табличным значением для соответствующего уровня значимости. Поскольку таблицы содержат критические значения коэффициента автокорреляции, то нулевая гипотеза может быть принята, если фактическое значение коэффициента меньше табличного.Когда фактическая величина коэффициента превышает табличное значение, нулевая гипотеза отвегается и признается наличие автокорреляции в исследуемом ряду.

Вычисление коэффициентов автокорреляции в динамических рядах в системе STATISTICA осуществляется аналогично рассмотренному ранее случаю с определением коэффициента автокорреляции в остатках тренда.

Рис. 106. Коэффициенты автокорреляции для импорта в 3 периоде

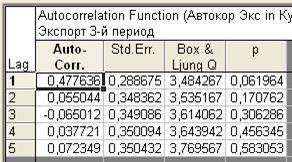
Рис. 108. Коэффициенты автокорреляции для экспорта в 3 периоде

Напомним, что в STATISTICA красным цветом высвечиваются статистически значимые оценки. Следовательно, можно сделать вывод об отсутствии автокорреляции в изучаемом динамическом ряду.

Поскольку в нашем примере отсутствует автокорреляция, построим авторегрессионную модель в методических целях, сместив исходный ряд на 1 лаг, т.е. модель первого порядка.

Для вычисления параметров уравнения авторегрессии потребуется создать дополнительную переменную . Воспользуемся тем же приемом, что и при расчете показателей изменения уровней динамического ряда. Выберем меню Statistics/Advanced Linear/Nonlinear Models/Times Series/Forecasting, в качестве переменной используем исходные данные третьего периода. Нажимаем кнопку ОК, переходим на закладку Shift и в поле Shift (Lag) Series Back ставим 1. Далее нажимаем ОК (Transform selected series) и сохраняем полученные данные с помощью кнопки Save variables. В результате получаем таблицу с двумя переменными, первая - исходный ряд, а вторая – ряд, смещенный на 1 период.

Длина переменных должна быть одинаковой, для чего нужно удалить в первом столбце последнюю и во втором - первую строки.

Процедура расчета численных значений коэффициентов уравнения авторегрессии идентична определению параметров уравнений для различных трендовых моделей и осуществляется с помощью меню Statistics/Multiple Regression. При этом в качестве зависимой переменной выбирается исходный ряд, в качестве независимой – ряд сдвинутый на лаг назад, так как нас интересует зависимость текущего уровня от предыдущего.

Рис. 110. Данные регрессионного анализа (импорт)

Рис. 111. Данные регрессионного анализа (экспорт)

Соответственно, уравнения авторегрессии имеют вид:

Как правило, авторегрессионная модель позволяет лучше, чем трендовая, описать предысторию процесса и получить более точный прогноз. Но для этого необходимо, чтобы уравнение и все его параметры были статистически значимы.

На основе данного уравнения сделаем прогноз на объем экспорта и импорта за 2006 года.

млрд. $ US составил объем импорта,

млрд. $ US составил объем экспорта.

Графики авторегрессий для экспорта и импорта Японии выглядят следующим образом:

Рис. 112. Авторегрессия для импорта в третьем периоде

Рис. 113. Авторегрессия для экспорта в третьем периоде

Корреляция рядов динамики

При изучении тенденции развития явления во времени часто возникает необходимость определить степень зависимости между динамическими рядами.

Корреляционная связь между уровнями двух динамических рядов называется кросс-корреляцией. Оценка тесноты связи в задачах исследования кросс-корреляции производится с использованием стандартного коэффициента корреляции Пирсона. Однако применение традиционных методов корреляции и регрессии к анализу зависимости временных рядов имеет определенные особенности.

смешанный корреляционный момент первой степени.

Величина коэффициента корреляции, который представляет собой нормированный показатель ковариации, в этих условиях может оказаться достаточно большой. Однако однонаправленность трендов и высокое значение коэффициента корреляции вовсе не означает наличие причинно-следственной зависимости между рядами. Поэтому, прежде чем приступать к количественной оценке корреляционной зависимости, необходимо теоретически обосновать ее наличие.

Вторая особенность обусловлена тем, что одним из условий применения КРА является независимость наблюдений. В контексте изучения временных рядов – это отсутствие связи между уровнями ряда, т.е. автокорреляции. Наличие тренда (автокорреляции) в анализируемых динамических рядах может существенно исказить оценку. Поэтому для получения адекватного результата, необходимо предварительно исключить тенденцию из анализируемых рядов.

Существует несколько способов исключения автокорреляции (тенденции). Один из них основан на переходе от корреляции уровней ряда к корреляции остатков, отклонений фактических уровней от тренда. При этом:

- определяют форму тренда и производят аналитическое выравнивание каждого из связных рядов;

- рассчитывают отклонения фактических уровней от соответствующих выровненных уровней по каждому ряду;

- определяют численное значение коэффициента корреляции по полученным отклонениям.

Если обозначить отклонение от тренда по ряду, содержащему результативный признак – , а по ряду, содержащему факторный признак - , то коэффициент корреляции можно рассчитать по следующей формуле:

В том случае, когда тенденция описывается уравнениями прямой или параболы, среднее отклонение от тренда всегда равно нулю. Для других типов тренда это равенство выполняется, если математическая функция достаточно точно отражает фактическую тенденцию.

Если , формула принимает вид:

Зная коэффициент корреляции, можно определить коэффициент регрессии, который для линейной зависимости будет определяться:

Свободный член уравнения в данном случае будет равен нулю, поскольку:

Таким образом, уравнение регрессии отклонений от тренда примет вид:

Практика показывает, что часто в отклонениях от тренда сохраняется автокорреляция. Прежде чем приступить к расчету коэффициента корреляции по остаткам, необходимо проверить наличие в них автокорреляции.

Наряду с коррелированием остатков, способом обойти автокорреляцию уровней может быть метод коррелирования последовательныхразностей или тех цепных показателей динамических рядов, которые являются константами их трендов. Так, для линейного тренда – это цепные абсолютные приросты ( и ), а коэффициент корреляции будет определяться по формуле:

Данный подход к исключению автокорреляции вполне оправдан. На длительном временном отрезке искажение корреляции при наличии тренда может быть весьма существенным, благодаря кумулятивному эффекту. В разностях между соседними уровнями воздействие тренда незначительно, т. к. в большей мере они отображают влияние колеблемости.

Если установлено, что тенденция ряда близка к экспоненте, рекомендуется коррелировать цепные темпы роста. При наличии в анализируемых рядах тенденций разного типа, допускается коррелирование разных цепных показателей, являющихся константами различных трендов.

Еще один прием устранения автокорреляции основан на включении времени в уравнение регрессиив качестве аргумента: .

Математически доказано, что непосредственное введение в уравнение регрессии фактора времени устраняет автокорреляцию, аналогично использованию отклонений фактических уровней от тренда. Это свойство, доказанное в теореме Фриша справедливо не только для линейной тенденции. Простота реализации этого подхода явилась причиной его широкого применения в практических исследованиях.

При изучении связи между временными рядами следует помнить, что между изменением уровней одного ряда, как отклика на изменение уровней другого, может существовать определенный временной лаг.

Коэффициенты кросс-корреляции на основе отклонений от трендов в STATISTICA рассчитываются точно так же, как и коэффициенты автокорреляции. Только на закладке Autocorrelations выбирается кнопка Crosscorrelations. Напомним, что это осуществляется с помощью меню Statistics/Advanced Linear/Nonlinear Models/Time Series Forecasting. И выбрать необходимо сразу две переменные: отклонения от лучших трендов одного и второго динамических рядов.

Рис. 114. Параметры кросс-корреляции

На основании рассчитанных коэффициентов кросс-корреляции определяется лаг наиболее существенной взаимосвязи между динамическими рядами, то есть тот лаг, которому соответствует максимальный коэффициент кросс-корреляции (помечается красным цветом). В нашем случае максимально значение достигается при и составляет r = 0,742002.

Это свидетельствует о статистически значимой тесноте связи между двумя динамическими рядами при , что является достаточным основанием возможности прогнозирования значений одного динамического ряда по соответствующим уровням другого и в данном случае нет необходимости в смещении их относительно друг друга.

Описанный выше прием непосредственного включения в уравнение связи фактора времени, позволяет не только оценить зависимость между рядами, но и получить модель для прогнозирования.

где i - лаг наибольшей взаимосвязи между рядами, в нашем случае .

В демонстрационном примере невозможно теоретически обосновать, какой из динамических рядов является признаком-фактором, а кокой признаком-результатом, т.е. обосновать причинно-следственную связь. Поэтому построим два уравнения, в которых в качестве результативной переменной будут выступать разные динамические ряды.

Расчет параметров этих факторно-временных функций осуществляется аналогично коэффициентам любого другого уравнения регрессии в меню Statistics/Multiple Regression. При построении уравнений в поле зависимых и независимых переменных меняем динамические ряды местами и добавляем переменную Т - время.

Рис. 116. Параметры факторно-временных функций

Рис. 117. Параметры факторно-временных функций

Для прогнозирования следует выбрать уравнение на основе максимального коэффициента детерминации из таблиц Regression Summary (или использовать другие критерии). При условии статистической значимости уравнения и параметров модель может быть использована для прогнозирования.

Максимальный коэффициент детерминации в 1 таблице. . В нашем случае мы используем уравнение, где признаком-результатом является третий период импорта, а признаком-фактором третий период экспорта и фактор времени:

где - значение уровня динамического ряда, рассчитанное по линейной модели авторегрессии первого порядка для экспорта Японии в 2006 году, поэтому кросс-корреляционная модель прогноза получится очень далекой от реальной тенденции. Так как фактических данных при прогнозировании не имеем. Рассчитаем как экспорт в 2006 году, спрогнозированный на основе лучшего тренда (полинома 3-ей степени).

Читайте также: