Пространственная система сил реферат

Обновлено: 30.06.2024

Магистерская диссертация состоит из 43 страниц, 20 рисунков, 1 таблицы. При составлении использовано 33 источника литературы. Магистерская диссертация состоит из введения, 4 глав, заключения, списка использованной литературы и приложения.

Ключевые слова: Цилиндрическая оболочка, Метод сил, Реактивное давление, Напряженно-деформированное состояние, линия контакта.

В введении обосновывается актуальность работы. Целью работы является разработка способа расчета тонкостенных пространственных систем, состоящих из сочлененных замкнутых цилиндрических оболочек, основанном на одном из методов строительной механики- методе сил.

В первой главе рассматриваются методы решения задач теории оболочек.

Во второй главе рассматриваются тонкостенные пространственные системы состоящие из ряда замкнутых цилиндрических оболочек. Предлагается такие пространственные системы рассчитывать методом сил. Одна из оболочек пространственной системы находится под действием сосредоточенной нагрузки. По линии контакта сочлененных оболочек возникает реактивное давление, величина и характер которого неизвестны. Для определения напряженно-деформированного состояния оболочек необходимо знать величину и характер изменения реактивного давления по линии контакта оболочек. Принимаем реакцию стенки оболочек равномерно распределенной в пределах сколь угодно малых участков, а всю эпюру - ограниченно ступенчатой линией. Перемещения определяются только для середин отдельных прямолинейных участков. Связь между оболочками осуществляется только в отдельных точках, находящихся в серединах прямолинейных участков эпюры. Условные опоры представлены в виде абсолютно твердых стержней-связей, присоединенных шарнирно к оболочкам. Основную статистически определимую систему выберем, разрезая или удаляя все вертикальные стержни, заменяя их действие действием неизвестных реактивных сил. Расчет пространственной системы, состоящей из двух одинаковых сочлененных цилиндрических оболочек, сводится к расчету замкнутой цилиндрической оболочки под действием сосредоточенных сил. Для нахождения неизвестных реактивных сил составляем канонические уравнения обычного вида. Значения перемещений стенки замкнутой цилиндрической оболочки под действием сосредоточенной силы можно найти по аналитическим выражениям. Перемещения стенки оболочки от внешней нагрузки, в зависимости от вида действия, можно определить по работам К.Ф. Шагивалеева. Подставив найденные перемещения в систему уравнений и разрешив последние, получим значения неизвестных реактивных сил. По ним находится интенсивность давления в пределах каждого участка. Имея величину и характер реактивного давления можно определить напряженно-деформированное состояние оболочек.

В третьей главе по предложенному способу проведен расчет тонкостенной пространственной системы, состоящей из двух одинаковых сочлененных замкнутых цилиндрических оболочек. Исследована зависимость максимального значения реактивного давления от того, насколько участков разбивается линия контакта оболочек пространственных систем, состоящих из сочлененных замкнутых цилиндрических оболочек методом сил.

В четвертой главе было рассмотрено влияние изменения геометрических параметров одной из оболочек на величину и характер распределения реактивного давления. Произведен расчет пространственных систем, состоящих из двух сочлененных замкнутых цилиндрических оболочек с различными параметрами при действии внутреннего равномерно распределенного давления.

Система сил, линии действия которых расположены в различных плоскостях, называется пространственной системой сил .

Пространственная система сил называется сходящейся , если линии действия всех сил системы пересекаются в одной точке.

Теорема: пространственная система сходящихся сил эквивалентна равнодействующей, которая равна векторной сумме этих сил; линия действия равнодействующей проходит через точку пересечения линий действия составляющих сил.

Пусть дана пространственная система n сходящихся сил (F₁, F₂, F₃. F_n) . На основании следствия из аксиом III и IV перенесем все силы системы вдоль линий действия в точку их пересечения. Затем на основании аксиомы параллелограмма последовательно сложим все силы и получим их равнодействующую:

Силовой многоугольник пространственной системы сил не лежит в одной плоскости, поэтому геометрический и графический способы нахождения равнодействующей пространственной системы сходящихся сил неприемлемы, а применяется только аналитический способ (метод проекций) .

Проекция силы на ось в пространстве находится по проецирующим перпендикулярам, и может быть определена при помощи тригонометрических функций. При определении проекций сил пространственной системы потребуется система координат с осями X , Y , Z , поскольку силы системы не располагаются в одной плоскости.

Правило знаков для проекций будет таким же, как и для плоской системы сил – совпадающие по направлению с координатной осью силы считаются положительными, в противном случае – отрицательными. Если вектор силы параллелен какой-либо оси координат, то он проецируется на эту ось в натуральную величину, если же вектор перпендикулярен оси, его проекция на эту ось будет равна нулю.

Разложение силы по трем осям координат

Пусть дана сила F (см. рисунок 1) .
Возьмем систему координат так, чтобы начало координат совпадало с началом вектора силы F (т. е. с точкой приложения силы). Из конца этого вектора опустим перпендикуляр на плоскость xy и разложим силу F на составляющие F_xy и F_z , а составляющую F_xy – на составляющие F_x и F_y . Тогда:

Достроим полученное изображение до параллелепипеда, у которого составляющие F_x , F_y и F_z являются ребрами, а сила F – диагональю.

Из изложенного можно сделать вывод: равнодействующая трех взаимно-перпендикулярных сил выражается по модулю и направлению диагональю параллелепипеда, построенного на этих силах .

Из рисунка видно, что в случаях разложения силы F по трем взаимно-перпендикулярным направлениям x , y , z составляющие F_x , F_y и F_z равны по модулю проекциям силы F на эти оси.

Зная проекции силы на три взаимно-перпендикулярные оси координат, можно определить модуль и направление вектора силы по формулам:

модуль силы: F = √(F_x 2 + F_y 2 + F_z 2 ) (здесь и далее √ - знак корня) ;

направляющие косинусы: cos(F,x) = Fx/F; cos(F,y) = Fy/F; cos(F,z) = Fz/F .

Аналитический способ определения равнодействующей пространственной системы сходящихся сил

Рассмотренный выше способ разложения силы F на три составляющие по направлению координатных осей x , y , z можно применить для каждой из сходящихся сил пространственной системы. Тогда вместо данной системы n сходящихся сил мы получим эквивалентную ей систему 3n сил, из которых n сил действуют по оси x , n сил – по оси y , и n сил – по оси z .
Равнодействующая проекций сил системы на ось x равна их геометрической сумме, то же самое можно сказать и о равнодействующих проекций сил на оси y и z .
Таким образом, систему 3n сил можно заменить эквивалентной ей системой трех сил, каждая из которых представляет собой равнодействующую проекций сил данной системы на ту или иную ось координат.

Проекции силы на три взаимно-перпендикулярные оси и составляющие силы, направленные по этим осям, равны по модулю, следовательно, проекции равнодействующей равны:

Очевидно, что равнодействующая трех взаимно перпендикулярных сил выражается по модулю и направлению диагональю параллелепипеда, построенного на этих силах, и по известным проекциям равнодействующей можно определить модуль и направление самой равнодействующей.

Аналитические условия равновесия пространственной системы сходящихся сил

Известно, что пространственная система сходящихся сил эквивалентна равнодействующей. Если такая система сил находится в равновесии, т. е. эквивалентна нулю, то можно сделать вывод, что равнодействующая этой системы равна нулю, а следовательно, и проекции равнодействующей тоже равны нулю, причем эти проекции равны сумме проекций составляющих.
Отсюда вытекают условия равновесия пространственной системы сходящихся сил:

ΣX = 0; ΣY = 0; ΣZ = 0 .

Эти условия формируются следующим образом: для равновесия пространственной системы сходящихся сил необходимо и достаточно, чтобы алгебраическая сумма проекций всех сил на каждую их трех координатных осей равнялась нулю.

Момент силы относительно оси

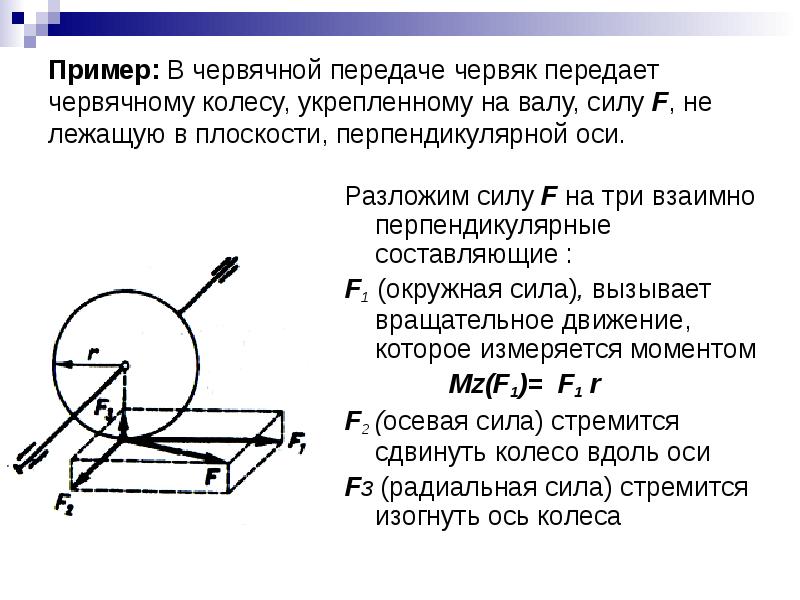
Рассмотрим колесо червячной передачи, укрепленное на валу, вращающемся в подшипниках (см. рисунок 2) . Червяк передает червячному колесу силу F , не лежащую в плоскости, перпендикулярной оси.

Разложим силу F на три взаимно-перпендикулярные составляющие F₁ , F₂ и F₃ .
Составляющую F₁ назовем окружной силой , составляющую F₂ – осевой силой , а составляющую F₃ – радиальной силой .
Из рисунка видно, что составляющая F₁ вызывает вращательное действие, которое измеряется произведением силы F₁ на радиус колеса r ; составляющая F₂ стремится сдвинуть червячное колесо вдоль оси, а составляющая F₃ стремится изогнуть ось колеса.
Очевидно, что вращающее действие сил F₂ и F₃ относительно оси колеса равно нулю.
Таким образом, если нужно найти момент силы относительно оси, то следует принимать в расчет только составляющую F₁ , лежащую в плоскости, перпендикулярной оси, и не пересекающую ось (иначе ее момент будет равен нулю).

Ранее было отмечено, что проекция вектора силы на ось есть скалярная алгебраическая величина. В отличие от проекции на ось проекция силы на плоскость есть величина векторная, так как эта проекция характеризуется не только числовым значением, но и положением на плоскости, т. е. направлением.
Поэтому моменту силы относительно оси можно дать такое определение: моментом силы относительно оси называется величина, равная моменту проекции этой силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с плоскостью.

Это определение поясняет рисунок 3 .
Момент силы относительно оси условимся записывать следующим образом:

Условимся считать момент силы положительным, если смотреть с положительного конца оси и сила стремится вызвать вращение против часовой стрелки, если же сила стремится вызвать вращение по часовой стрелке, ее момент считаем отрицательным.

Момент силы относительно оси не меняется при перемещении силы вдоль оси ее действия.

если вектор силы параллелен оси, так как при этом проекция силы на плоскость, перпендикулярную оси, равна нулю (см. рисунок 3, сила F_Z) ;
если линия действия силы пересекает ось, так как при этом плечо равно нулю (сила F₃ на рисунке 2) .

Аналитические условия равновесия пространственной системы произвольно расположенных сил

Пространственная система сил, в которой линии действия составляющих сил расположены произвольно, т. е. линии их действия могут не пересекаться и находиться в разных плоскостях, называется произвольно расположенной системой сил.

Для равновесия пространственной системы произвольно расположенных сил необходимо и достаточно, чтобы алгебраическая сумма проекций всех сил на каждую из трех осей координат была равна нулю и чтобы алгебраическая сумма моментов всех сил относительно каждой из этих осей была равна нулю.

Строгое обоснование приведенного выше условия равновесия пространственной системы произвольно расположенных сил требует знания некоторых вопросов, не предусмотренных программами учреждений среднего профессионального образования, поэтому условие равновесия такой системы здесь приводится без доказательства.

Математически условие равновесия пространственной системы произвольно расположенных сил можно записать в виде уравнений:

ΣX = 0; ΣMx(Fi) = 0;
ΣY = 0; ΣMy(Fi) = 0;
ΣZ = 0; ΣMz(Fi) = 0.

Свободное тело в пространстве имеет шесть степеней свободы, а именно: возможность перемещаться в направлениях трех взаимно-перпендикулярных осей координат и возможность вращаться вокруг этих осей. Таким образом, шести степеням свободы тела в пространстве соответствуют шесть условий равновесия.
Если система сил, приложенных к свободному телу, удовлетворяет всем шести условиям равновесия, то возможность трех перемещений и трех вращений тела под действием сил системы исключена, поэтому тело будет находится в равновесии.

Очевидно, что все выведенные ранее условия равновесия для различных систем сил являются частными случаями условия равновесия пространственной системы произвольно расположенных сил.

Так как условия равновесия пространственной системы сил справедливы для любых прямоугольных осей координат, то при решении данной задачи систему координат можно изменять, т. е. часть уравнений равновесия составить для одних осей координат, а часть – для измененных. В некоторых случаях этот прием упрощает решение задач.

Теорема о моменте равнодействующей относительно оси
(теорема Вариньона)

Теорема: момент равнодействующей относительно оси равен алгебраической сумме моментов, составляющих сил относительно этой же оси .

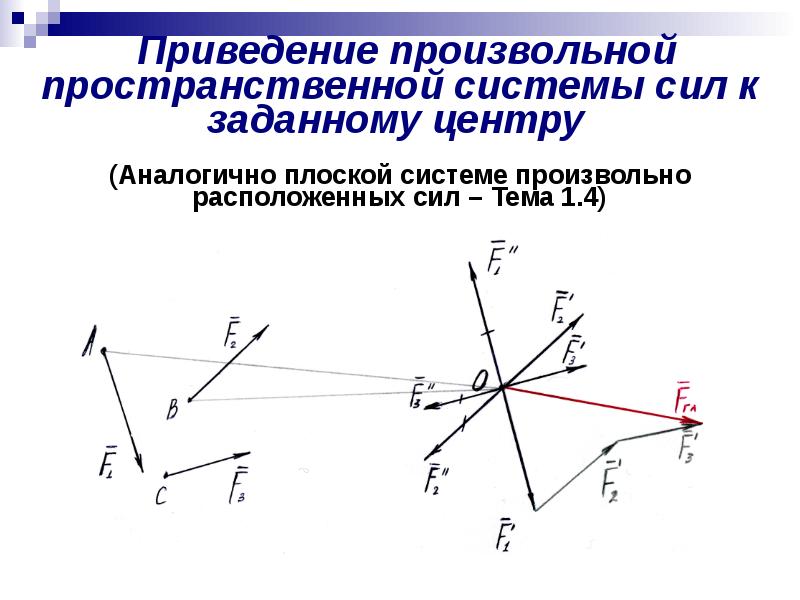
Пусть даны пространственная система n произвольно расположенных сил, приложенных к телу, и равнодействующая этой системы сил F_Σ (см. рисунок 4) :

Приложим к телу другую систему сил, равнодействующая которой F’_Σ по модулю равна F_Σ и направлена по той же линии действия, но в противоположную сторону, т. е. является уравновешивающей данной системы сил.
Тогда можно записать:

Так как обе записанные выше системы сил эквивалентны нулю, т. е. уравновешены, то к ним можно применить любое условие равновесия, например

Вы можете изучить и скачать доклад-презентацию на тему Пространственная система сил. (Тема 1.5). Презентация на заданную тему содержит 23 слайдов. Для просмотра воспользуйтесь проигрывателем, если материал оказался полезным для Вас - поделитесь им с друзьями с помощью социальных кнопок и добавьте наш сайт презентаций в закладки!

Знать: - момент силы относительно оси, свойства момента; - аналитический способ определения равнодействующей; -условия равновесия.

Уметь: -выполнять разложение силы на три взаимно перпендикулярные оси; -определять момент силы относительно оси; -определять реакции в опорах и выполнить проверку.

Пространственная система сил- система сил, линии действия которых расположены в различных плоскостях.

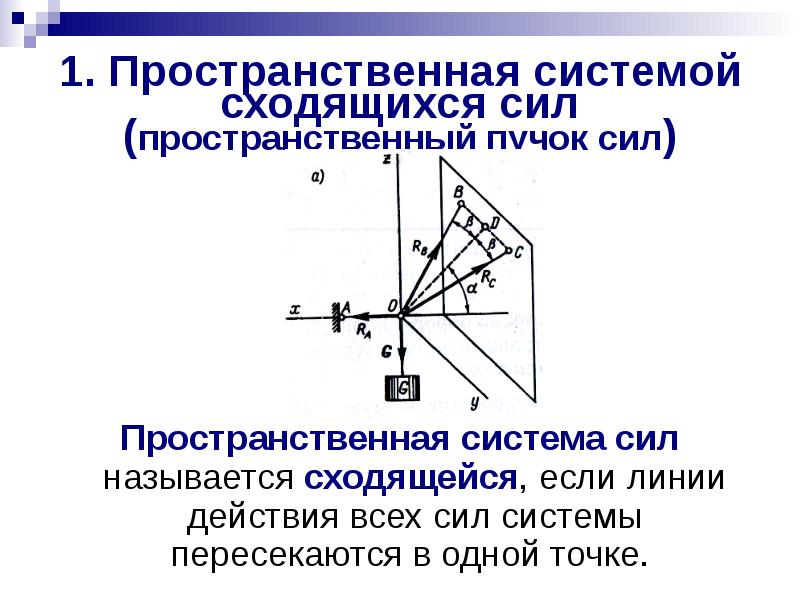
1. Пространственная системой сходящихся сил (пространственный пучок сил) Пространственная система сил называется сходящейся, если линии действия всех сил системы пересекаются в одной точке.

Теорема о равнодействующей пространственной ССС. Пространственная система сходящихся сил эквивалентна равнодействующей, которая равна векторной сумме этих сил; линия действия равнодействующей проходит через точку пересечения линий действия составляющих сил системы. F =Fi

Способы определения равнодействующей силы пространственной системы сходящихся сил: Способы определения равнодействующей силы пространственной системы сходящихся сил: Силовой многоугольник пространственной системы сил не лежит в одной плоскости, поэтому геометрический и графический способы нахождения равнодействующей неприемлемы. Применяется только аналитический способ ( метод проекций).

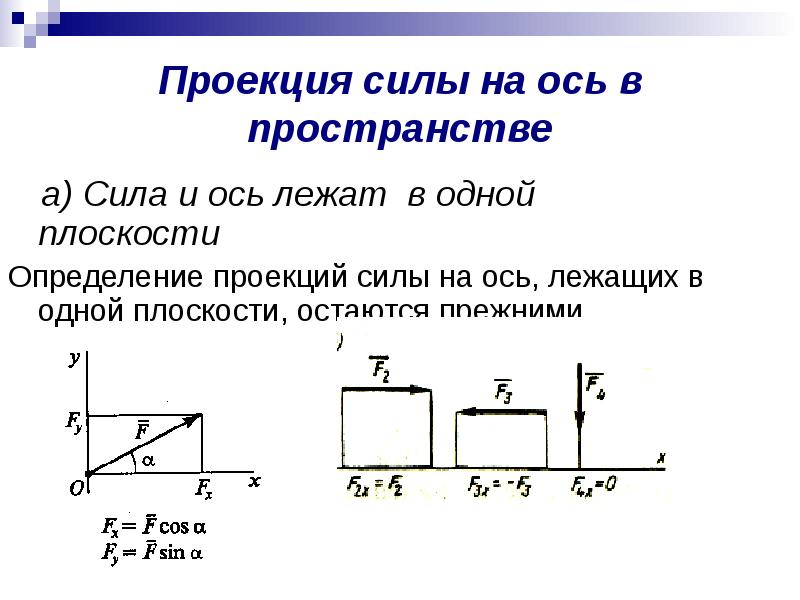
Проекция силы на ось в пространстве а) Сила и ось лежат в одной плоскости Определение проекций силы на ось, лежащих в одной плоскости, остаются прежними.

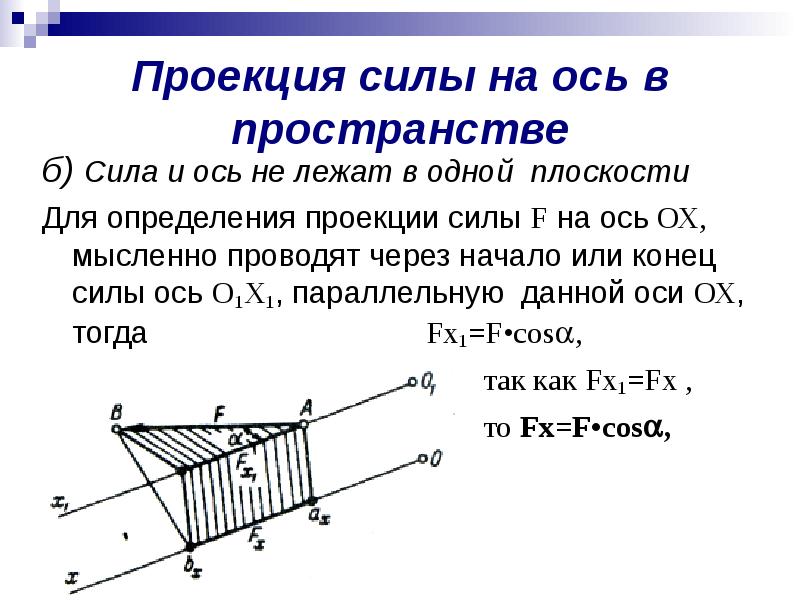
Проекция силы на ось в пространстве б) Сила и ось не лежат в одной плоскости Для определения проекции силы F на ось ОХ, мысленно проводят через начало или конец силы ось О1Х1, параллельную данной оси ОХ, тогда Fx1=F•cos, так как Fx1=Fx , то Fx=F•cos,

Разложение силы по трём осям координат Равнодействующая трёх взаимно перпендикулярных сил равна по модулю и направлена по диагонали параллелепипеда, построенного на этих силах. F=Fx+Fy+Fz

Модуль и направление равнодействующей силы : - модуль FƩ FƩ=Fx2+Fy2+Fz2 =(∑Xi)2+(∑Yi)2+(∑Zi)2 - направление FƩ Cos(FƩ,X)=Fx/FƩ=∑Xi/FƩ Cos(FƩ,Y)=Fy/FƩ= ∑Yi/FƩ Cos(FƩ,Z)=Fz/FƩ= ∑Zi/FƩ

Аналитическое условие равновесия пространственной ССС Для равновесия пространственной ССС необходимо и достаточно, чтобы равнодействующая системы, а значит и её проекции на оси координат X,Y и Z были равны 0. 1)Fix = Х = 0 FƩ = 0 2)Fiy = У = 0 3) Fiz = Z = 0

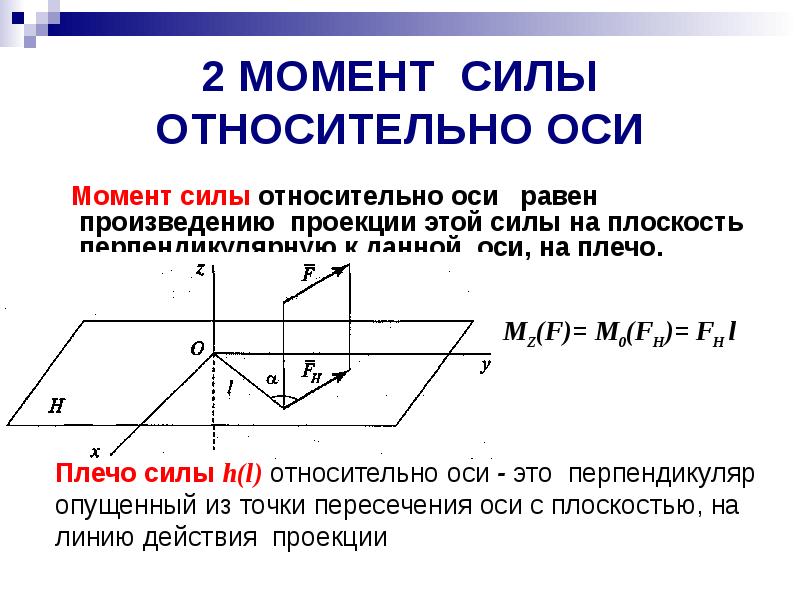
2 МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ОСИ Момент силы относительно оси равен произведению проекции этой силы на плоскость перпендикулярную к данной оси, на плечо.

Правило знаков Момент силы относительно оси будем считать положительным , если сила стремится вызвать вращение против часовой стрелки, момент силы считаем отрицательным, если она стремится вызвать вращение по часовой стрелке. При этом необходимо смотреть на плоскость перпендикулярно данной оси с её положительного конца.

Момент силы относительно оси равен нулю в 2 случаях: 1. Если линия действия силы перпендикулярна оси F1Z , т.к. h(l) = 0 2. Если вектор силы параллелен оси F2Z , т.к. FH = 0

Пример: В червячной передаче червяк передает червячному колесу, укрепленному на валу, силу F, не лежащую в плоскости, перпендикулярной оси. Разложим силу F на три взаимно перпендикулярные составляющие : F1 (окружная сила), вызывает вращательное движение, которое измеряется моментом Мz(F1)= F1 r F2 (осевая сила) стремится сдвинуть колесо вдоль оси Fз (радиальная сила) стремится изогнуть ось колеса

3. Пространственная система произвольно расположенных сил - это система сил, линии действия, которых не лежат в одной плоскости и не пересекаются в одной точке

Приведение произвольной пространственной системы сил к заданному центру (Аналогично плоской системе произвольно расположенных сил – Тема 1.4)

Модуль и направление главного вектора : - модуль FГЛ FГЛ=Fx2+Fy2+Fz2 =(∑Xi)2+(∑Yi)2+(∑Zi)2 - направление FГЛ Cos(Fгл; x)= Xi/ Fгл Cos(Fгл; y)= Yi/ Fгл Cos(Fгл; z)= Zi/ Fгл

Модуль главного момента : Алгебраическая сумма моментов всех сил системы относительно каждой оси. МГЛ =  (МX(Fi))2+(МY(Fi))2+ (МZ(Fi))2

Аналитические условия равновесия пространственной системы произвольно расположенных сил Алгебраическая сумма проекций всех сил на три взаимно перпендикулярные оси координат должна быть равна нулю и алгебраическая сумма моментов всех сил, относительно тех же осей, должна быть равна нулю