Принцип максимального правдоподобия реферат

Обновлено: 05.07.2024

Метод наибольшего правдоподобия в его современном виде был предложен английским статистиком Р. Фишером (1912), однако в частных формах метод использовался К. Гауссом, а еще раньше, в 18 веке, к его идее были близки И. Ламберт и Д. Бернулли. Следует добавить, что название "Метод наибольшего правдоподобия" является калькой с английского "maximum, likelihood, method".

Содержание работы

Файлы: 1 файл

Метод наибольшего правдоподобия.doc

Метод наибольшего правдоподобия…………………………………………… .3

Дискретные случайные величины………………………………………. 3

Непрерывная случайная величина………………………………………..4

Метод наибольшего правдоподобия

Метод наибольшего правдоподобия точечной оценки неизвестных параметров заданного распределения сводится к отысканию максимума функции одного или нескольких оцениваемых параметров, в качестве оценок выбираются те значения параметров, при которых данные результаты наблюдений "наиболее вероятны".

Дискретные случайные величины

Пусть X —дискретная случайная величина, которая в результате п опытов приняла возможное значение. Допустим что вид закона распределения величины X задан, но неизвестен параметр в, которым определяется этот закон требуется найти его точечную оценку

Обозначим вероятность того, что в результате испытания величина примет значение через р (Xi;Ө).

Функцией правдоподобия дискретной случайной величины X называют функцию аргумента Ө:

L(х1, х2, … , хп;)= р(х1; Ө)* р(х2; Ө) … р(хп; Ө)

Оценкой наибольшего правдоподобия параметра Ө называют такое его значение Ө*, при котором функция правдоподобия достигает максимума.

Функции L и ln L , достигают максимума при одном и том же значении Ө, поэтому вместо отыскания максимума функции L ищут, что удобнее, максимум функции In L.

Логарифмической функцией правдоподобия называют функцию ln L.

Точку максимума функции In L аргумента Ө можно искать, например, так:

1. Найти производную

2. Приравнять производную нулю и найти критическую точку Ө* -корень полученного уравнения (его называют уравнением правдоподобия).

3. Найти вторую производную

если вторая производная при Ө=Ө* отрицательная, то Ө* - точка максимума.

Найденную точку максимума Ө* принимают в качестве оценки наибольшего правдоподобия параметра Ө.

Непрерывная случайная величина

Пусть X — непрерывная случайная величина, которая в результате п испытаний приняла значения х1, х2, … , хп. Допустим, что вид плотности распределения - функции f(х)- задан, но неизвестен параметр Ө, которым определяется эта функция.

Функцией правдоподобия непрерывной случайной величины X называют функцию аргумента Ө:

L(х1, х2, … , хп;)= f(х1; Ө) * f(х2; Ө) * …* f(хп; Ө)

Оценку наибольшего правдоподобия неизвестного параметра распределения непрерывной случайной величины ищут так же как в случае дискретной случайной величины.

Если плотность распределения f(х) непрерывной случайной величины определяется двумя неизвестными параметрами Ө1 и Ө2, то функция правдоподобия есть функция двух независимых аргументов Ө1 и Ө2:

L(х1, х2, … , хп;)= f(х1; Ө) * f(х2; Ө) * …* f(хп; Ө)

Далее находят логарифмическую функцию правдоподобия и для отыскания ее максимума составляют и решают систему

Метод наибольшего правдоподобия не всегда приводит к приемлемым результатам, однако в достаточно широком круге практически важных случаев этот метод является в известном смысле наилучшим. Так, например, можно утверждать, что если для параметра существует несмещенная эффективная оценка Ө* по выборке объема n, то уравнение правдоподобия имеет единств, решение Ө=Ө*. Что касается асимптотического поведения оценок максимального правдоподобия при больших n, то известно, что при некоторых общих условиях метод наибольшего правдоподобия приводит к состоятельной оценке, которая асимптотически нормальна и асимптотически эффективна. Данные выше определения непосредственно обобщаются и на случай нескольких неизвестных параметров и на случай выборок из многомерных распределений.

Метод наибольшего правдоподобия состоит в том, что в качестве оценки параметра берется значение, при котором функция правдоподобия достигает своего максимума.

Параметр Ө находят, решая относительно Ө* уравнение

Часто вместо (1.2.3) используют уравнение

Если плотность или вероятности зависят от параметров, то наиболее правдоподобную оценку системы параметров получают решением системы уравнений

Наиболее правдоподобные оценки имеют некоторые замечательные свойства. При достаточно общих условиях они являются состоятельными и асимптотически нормально распределенными (однако не всегда несмещенными), имеют среди всех асимптотически нормально распределенных оценок наибольшую эффективность. Справедливо следующее положение: если вообще имеется эффективная оценка, то она получается методом наибольшего правдоподобия.

Если функция правдоподобия является дифференцируемой по переменным , то о.н.п. удовлетворяет следующей системе уравнений:

Это хорошо известные из курса математического анализа необходимые условия экстремума функции нескольких переменных.

Оценить вероятность некоторого события . Пусть

Решение. ; . Пусть в независимых наблюдениях событие произошло раз, т.е. . Таким образом, имеем , . Отсюда следует, что . Следовательно, есть наиболее правдоподобная оценка параметра . Случайная величина k биномиально распределена, ; Следовательно, — несмещенная оценка вероятности, асимптотически состоятельная и асимптотически нормальная.

Рассмотрим независимую выборку из равномерного распределения в отрезке , где -- неизвестный параметр. Выпишем функцию правдоподобия

и перепишем ее в более удобном виде:

Легко видеть, что максимальное значение эта функция принимает в точке . Это и есть искомая оценка наибольшего правдоподобия для параметра .

Принцип максимального правдоподобия является спорным принципом статистического вывода, который предполагает, что вся информация о статистической выборке содержится в функции правдоподобия.

Функция правдоподобия основывается на условной вероятности взятием ее как функции от второго аргумента при фиксировании первого. Например рассмотрим модель в которой плотность вероятности случайной величины X зависит от параметра θ. Тогда для некоторого конкретного значения x случайной величины X функция L(θ | x) = P(X=x | θ) и есть функция правдоподобия θ, определяющая насколько правдоподобно каждое конкретное значение параметра θ при условии, что нам известно значение x величины X. Две функции правдоподобия являются равными, если одна есть произведение второй на некоторую скалярную величину.

Содержание

Пример

Рассмотрим случайные величины

X количество успехов в двенадцати независимых испытаний с распределением Бернулли с вероятностью успеха θ в каждом из них.
Y количество независимых испытаний с распределением Бернулли, необходимых для получения трех успехов. Вероятность успеха в каждом из испытаний θ.

Тогда рассмотрение X = 3 даст функцию правдоподобия

$L(\theta|X=3)=\begin 12\\3\end\;\theta^3(1-\theta)^9=220\;\theta^3(1-\theta)^9$

а рассмотрение Y = 12 даст функцию правдоподобия

$L(\theta|Y=12)=\begin 11\\2\end\;\theta^3(1-\theta)^9=55\;\theta^3(1-\theta)^9.$

Они равносильны, так как одна равняется произведению второй на скалярное значение. Принцип максимального правдоподобия в данном случае говорит, что выводы, сделанные о значении переменной θ должны быть одинаковы в обоих случаях.

Разница в наблюдении X = 3 и наблюдении Y = 12 исключительно в дизайне эксперимента: в одном случае изначально было решено делать двенадцать попыток, а в другом делать попытки, пока не будет трех успешных. Результат будет одинаковым в обоих случаях. Поэтому принцип максимального правдоподобия иногда выражают следующим образом:

Вывод должен зависеть только от исхода эксперимента, а не от дизайна эксперимента.

Закон максимального правдоподобия

Связанная с принципом максимального правдоподобия концепция — это закон максимального правдоподобия, говорящий, что отношение того, какое значение параметра более применимо, равняется отношению их функций правдоподобия. Тогда отношение

$\Lambda = <L(a|X=x) \over L(b|X=x)> =$

является мерой того, насколько величина x принимает параметр a в отношении к b. Таким образом, если отношение равняется 1, то разницы нет, а если больше 1, то a предпочтительней b, и наоборот.

Из принципа максимального правдоподобия и закона максимального правдоподобия следует, что параметр, который максимизирует функцию правдоподобия, является лучшим. Это и является основой широко известного метода максимального правдоподобия.

Историческая справка

Принцип максимального правдоподобия был впервые упомянут в печати в 1962 г. Однако основы принципа и применение его на практике были опубликованы ранее в работах Р. А. Фишера в 1920 г.

Аргументы за и против принципа максимального правдоподобия

Принцип максимального правдоподобия принимается не всеми. Некоторые широко используемые методы традиционной статистики, как например проверка статистических гипотез противоречат принципу максимального правдоподобия. Рассмотрим кратко некоторые за и против этого принципа.

Зависимость результата от организации эксперимента

Неосуществленные события действительно играют роль в некоторых общих статистических методах. Например результат проверки статистической гипотезы может зависеть от доверительной вероятности так же или даже более, чем распределение неизвестного параметра. А сама доверительная вероятность может зависеть организации эксперимента.

Некоторые классичекие методы проверки гипотез базируются не на правдоподобии. Часто приводимый пример это проблема оптимальной остановки. Предположим я сказал, что бросил монету 12 раз и получил 3 решки. Из этого вы сможете сделать некоторые выводы о вероятности выпадения решки у этой монеты. А теперь предположим, что я бросал монету пока решка не выпала 3 раза, и получилось 12 бросков. Сделаете ли вы теперь другие выводы?

Функция правдоподобия одинакова в обоих случаях и пропорциональна

$p^3 \; (1-p)^9$

В соответствии с принципом правдоподобия выводы должны быть одинаковы в обоих случаях.

Предположим некоторая группа ученых определяет вероятность некоторого исхода (который мы будем называть 'успехом') серией экспериментов. Здравый смысл подсказывает нам, что если нет оснований считать что успех более вероятен, чем неудача, и наоборот, то следует положить вероятность успеха равной 0.5. Ученый Адам сделал 12 испытаний, в которых получил 3 успеха и 9 неудач, после чего умер.

$\left(<12 \choose 9> Его коллега по лаборатории Билл продолжил работу Адама и опубликовал результат проверки гипотезы. Он проверил гипотезу что вероятность успеха p=0.5 против p +++\right)\left(\right)^$

что есть 299/4096 = 7.3 %. Таким образом гипотеза не отвергается при 5 % уровне доверия.

Шарлотта, прочитав статью Билла, пишет письмо. Она считает, что Адам, возможно, продолжал испытания пока не умер, успев получить к этому моменту 3 успеха. Вероятность того, что для трех успехов потребуется 12 или более испытаний равна

$1-\left(<10 \choose 2> \left(\right)^+\left(\right)^+\cdots +\left(\right)^\right)$

что есть 134/4096 = 3.27 %. И теперь результат отвергается при уровне в 5 %.

Для этих ученых зависимость результата испытаний зависит от организации эксперимента, а не только от правдоподобия результата.

Очевидно, парадоксы такого рода некоторые считают аргументом против принципа правдоподобия, для других они же иллюстрирует значимость принципа.

Эта система соответствует системе, полученной по методу наименьших квадратов. То есть ММП и МНК дают одинаковые результаты, если соблюдаются предпосылки МНК. Последнее выражение в системе (2.54) дает оценку дисперсии случайной переменной 7, или, что одно и то же, дисперсии случайных остатков. Как было отмечено выше (см. формулу (2.23)), несмещенная оценка дисперсии случайных остатков равна… Читать ещё >

Метод максимального правдоподобия ( реферат , курсовая , диплом , контрольная )

Метод максимального правдоподобия (ММП) является одним из наиболее широко используемых методов в статистике и эконометрике. Для его применения необходимо знание закона распределения исследуемой случайной величины.

Пусть имеется некоторая случайная величина У с заданным законом распределения ДУ). Параметры этого закона неизвестны и их нужно найти. В общем случае величину Y рассматривают как многомерную, т. е. состоящую из нескольких одномерных величин У1, У2, У3 …, У.

Предположим, что У — одномерная случайная величина и ее отдельные значения являются числами. Каждое из них (У], у2, у3, …, у") рассматривается как реализация не одной случайной величины У, а ? случайных величин У1; У2, У3 …, У". То есть:

уj — реализация случайной величины У];

у2 — реализация случайной величины У2;

уз — реализация случайной величины У3;

у" - реализация случайной величины У".

Параметры закона распределения вектора У, состоящего из случайных величин Yb Y2, У3, У", представляют как вектор ?, состоящий из к параметров: . ?2,вк. Величины ?? ?2, У3,…, ?? могут быть распределены как с одинаковыми параметрами, так и с различными; некоторые параметры могут совпадать, а другие различаться. Конкретный ответ на этот вопрос зависит от той задачи, которую решает исследователь.

Например, если стоит задача определения параметров закона распределения случайной величины У, реализацией которой являются величины У1; У2, У3, У," то предполагают, что каждая из этих величин распределена так же, как величина У. Иначе говоря, любая величина У,• описывается одним и тем же законом распределения/(У,•), причем с одними и теми же параметрами ?: . ?2,…, дк.

В рамках метода максимального правдоподобия совокупность имеющихся значений У], у2, у3, …, у" рассматривается как некоторая фиксированная, неизменная. То есть закон /(У;) есть функция от заданной величиныу, и неизвестных параметров ?. Следовательно, для п наблюдений случайной величины У имеется п законов /(У;).

Неизвестные параметры этих законов распределения рассматриваются как случайные величины. Они могут меняться, однако приданном наборе значений Уі, у2, у3, …, у" наиболее вероятны конкретные значения параметров. Иначе говоря, вопрос ставится таким образом: каковы должны быть параметры ?, чтобы значения уj, у2, у3, …, у" были наиболее вероятны?

Для ответа на него нужно найти закон совместного распределения случайных величин У1; У2, У3,…, Уп -КУі, У2, Уз, У"). Если предположить, что наблюдаемые нами величиныу^ у2, у3, …, у" независимы, то он равен произведению п законов/.

(У;) (произведению вероятностей появления данных значений для дискретных случайных величин или произведению плотностей распределения для непрерывных случайных величин):

Чтобы подчеркнуть тот факт, что в качестве переменных рассматриваются искомые параметры ?, введем в обозначение закона распределения еще один аргумент — вектор параметров ?:

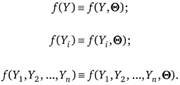
С учетом введенных обозначений закон совместного распределения независимых величин с параметрами будет записан в виде.

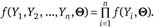
(2.51).

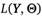
Полученную функцию (2.51) называют функцией максимального правдоподобия и обозначают :

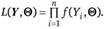
Еще раз подчеркнем тот факт, что в функции максимального правдоподобия значения У считаются фиксированными, а переменными являются параметры вектора (в частном случае — один параметр). Часто для упрощения процесса нахождения неизвестных параметров функцию правдоподобия логарифмируют, получая логарифмическую функцию правдоподобия

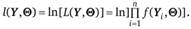
Дальнейшее решение по ММП предполагает нахождение таких значений ?, при которых функция правдоподобия (или ее логарифм) достигает максимума. Найденные значения ?; называют оценкой максимального правдоподобия.

Методы нахождения оценки максимального правдоподобия достаточно разнообразны. В простейшем случае функция правдоподобия является непрерывно дифференцируемой и имеет максимум в точке, для которой.

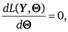
В более сложных случаях максимум функции максимального правдоподобия не может быть найден путем дифференцирования и решения уравнения правдоподобия, что требует поиска других алгоритмов его нахождения, в том числе итеративных.

Оценки параметров, полученные с использованием ММП, являются:

— состоятельными, т. е. с увеличением объема наблюдений разница между оценкой и фактическим значением параметра приближается к нулю;
— инвариантными: если получена оценка параметра ?, равная 0L, и имеется непрерывная функция q (0), то оценкой значения этой функции будет величина q (0L). В частности, если с помощью ММП мы оценили величину дисперсии какого-либо показателя (af), то корень из полученной оценки будет оценкой среднего квадратического отклонения (?,), полученной по ММП.
— асимптотически эффективными;
— асимптотически нормально распределенными.

Последние два утверждения означают, что оценки параметров, полученные по ММП, проявляют свойства эффективности и нормальности при бесконечно большом увеличении объема выборки.

Для нахождения параметров множественной линейной регрессии вида ["https://referat.bookap.info", 16].

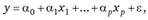
необходимо знать законы распределения зависимых переменных 7; или случайных остатков . Пусть переменная Yt распределена по нормальному закону с параметрами ?,•, ?,•. Каждое наблюдаемое значение у, имеет, в соответствии с определением регрессии, математическое ожидание ?,• = МУ" равное его теоретическому значению при условии, что известны значения параметров регрессии в генеральной совокупности.

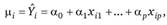
где xfl, …, xip — значения независимых переменных в і-м наблюдении. При выполнении предпосылок применения МНК (предпосылок построения классической нормальной линейной модели), случайные величины У, имеют одинаковую дисперсию.

Дисперсия величины определяется по формуле.

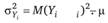
Преобразуем эту формулу:

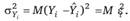
(2.52).

При выполнении условий Гаусса — Маркова о равенстве нулю математического ожидания случайных остатков и постоянстве их дисперсий можно перейти от формулы (2.52) к формуле.

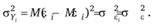
Иначе говоря, дисперсии случайной величины У, — и соответствующих ей случайных остатков совпадают.

Выборочную оценку математического ожидания случайной величины Yj будем обозначать.

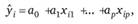
а оценку ее дисперсии (постоянной для разных наблюдений) как Sy.

Если предположить независимость отдельных наблюдений yit то получим функцию максимального правдоподобия.

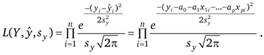
(2.53).

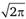
В приведенной функции делитель является константой и не оказывает влияния на нахождение ее максимума. Поэтому для упрощения расчетов он может быть опущен. С учетом этого замечания и после логарифмирования функция (2.53) примет вид.

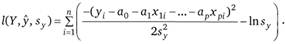
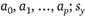
В соответствии с ММП найдем производные логарифмической функции правдоподобия по неизвестным параметрам

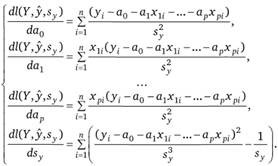
Для нахождения экстремума приравняем полученные выражения к нулю. После преобразований получим систему.

(2.54).

Аналогичная оценка, полученная с применением ММП (как следует из системы (2.54)), вычисляется по формуле.

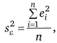
т.е. является смещенной.

Мы рассмотрели случай применения ММП для нахождения параметров линейной множественной регрессии при условии, что величина У, нормально распределена. Другой подход к нахождению параметров той же регрессии заключается в построении функции максимального правдоподобия для случайных остатков . Для них также предполагается нормальное распределение с параметрами (0, ??). Нетрудно убедиться, что результаты решения в этом случае совпадут с результатами, полученными выше.

Аннотация: Цель работы: практически освоить метод максимального правдоподобия для точечной оценки неизвестных параметров заданного вероятностного распределения случайной величины. Среда программирования — MATLAB.

Теоретическая часть

Метод максимального или наибольшего правдоподобия предложен Р. Фишером [6, 13]. С помощью этого метода производится точечная оценка неизвестных параметров априорно известного закона распределения случайной величины.

Рассмотрим сначала суть метода при оценке параметров дискретного распределения случайной величины [6].

Обозначим вероятность того, что в результате испытания величина примет значение \mbox< >(i=1,2. n)" />
, через .

Определение. Функцией правдоподобия случайной дискретной величины называют функцию аргумента :

$L(x_1,x_2. x_n;\theta)=p(x_1;\theta)p(x_2;\theta) . p(x_n;\theta),$

( 7.1)

где ,\mbox< >x_. x_" />
— фиксированные числа, полученные при измерении случайной величины .

В качестве точечной оценки параметра принимают такое его значение =\theta^(x_1,x_2. x_n)" />
, при котором функция правдоподобия достигает максимума. Оценку " />
называют оценкой максимального правдоподобия .

Для упрощения расчетов в рассмотрение вводится логарифм функции правдоподобия , которую называют логарифмической функцией правдоподобия . Функции и достигают максимума при одном и том же значении своего аргумента, поэтому вместо отыскания максимума функции ищут максимум функции . Записывая необходимое условие экстремума функции правдоподобия в случае скалярного параметра, получаем уравнения правдоподобия

$\frac<\partial L(\vec x_n;\theta)><\partial \theta>=0,$

( 7.2)

$\frac<\partial\ln L(\vec x_n;\theta)><\partial \theta>=0,$

( 7.3)

$\vec x_n$

где — заданная выборка случайных величин.

Уравнение правдоподобия (7.3) с логарифмической функцией, как правило, более простое относительно функции правдоподобия (7.2).

Если распределение случайной величины зависит от вектора параметров , то уравнение (7.3) заменяется системой уравнений

$\frac<\partial\ln L(\vec x_n;\theta)><\partial \theta_k>=0,\qquad k=\overline.$

( 7.4)

Именно уравнения (7.3) и (7.4) принято называть уравнениями правдоподобия [13]. Во многих случаях решение системы (7.4), являющейся, как правило, нелинейной, приходится искать численными методами.

Рассмотрим применение метода максимального правдоподобия для оценки параметров непрерывного распределения случайных величин генеральной совокупности .

Пусть — непрерывная случайная величина , которая в результате испытаний приняла значения ,\mbox< >x_. x_" />
. Предполагается, что вид плотности распределения задан, но неизвестен параметр , которым определяется эта функция .

Определение. Функцией правдоподобия непрерывной случайной величины называют функцию аргумента

$L(x_1,x_2. x_n;\theta)=f(x_1;\theta)f(x_2;\theta) . f(x_n;\theta),$

( 7.5)

$x_<1> где ,\mbox< >x_. x_$
— фиксированные числа.

$\theta$

Оценку максимального правдоподобия неизвестного параметра распределения непрерывной случайной величины ищут так же, как в случае дискретной величины.

Замечание. Если плотность распределения непрерывной случайной величины определяется двумя неизвестными параметрами и , то функция правдоподобия является функцией двух независимых аргументов и :

$L(x_1,x_2. x_n;\theta_1,\theta_2)=f(x_1;\theta_1,\theta_2)f(x_2;\theta_1,\theta_2) . f(x_n;\theta_1,\theta_2),$

( 7.6)

Как для дискретных распределений, так и для непрерывных точку максимума логарифмической функции распределения аргумента можно искать через необходимое условие экстремума :

Найденную точку максимума " />
принимают в качестве оценки максимального правдоподобия параметра .

Метод максимального правдоподобия имеет ряд достоинств: его оценки, вообще говоря, состоятельны (но они могут быть смещенными), распределены асимптотически нормально (при больших значениях приближенно нормально) и имеют наименьшую дисперсию по сравнению с другими асимптотически нормальными оценками; если для оцениваемого параметра существует эффективная оценка " />
, то уравнение правдоподобия имеет единственное решение " />
; этот метод наиболее полно использует данные выборки об оцениваемом параметре, поэтому он особенно полезен в случае малых выборок. Недостаток метода состоит в том, что он часто требует сложных вычислений.

Практическая часть

1. Оценка параметра экспоненциального распределения

$\lambda$

Рассматривается пример поиска методом максимального правдоподобия оценки параметра экспоненциального распределения случайной величины, для которой функция плотности имеет вид

( 7.7)

К характеристикам экспоненциального распределения относятся математическое ожидание и дисперсия :

$M[X]=\frac<1><\lambda>,$

( 7.8)

$D[X]=\frac<1><\lambda^2>.$

( 7.9)

Замечание. Во встроенных функциях MATLAB параметром экспоненциального распределения является математическое ожидание случайной величины.

Возможная программная реализация точечной оценки параметра экспоненциального распределения:

Видоизмените программу так, чтобы параметры задачи вводились в одном диалоговом окне .
В соответствии с номером компьютера задайте следующие значения параметра:

№ 1: ; № 2: ; № 3: ; № 4: ; № 5: ;

№ 6: ; № 7: ; № 8: ; № 9: ; № 10: .

Число прогонов программы выберите по равномерному закону из следующих интервалов (в соответствии с номером компьютера):

Читайте также: