Предельная ошибка повторной и бесповторной случайной выборки реферат

Обновлено: 08.07.2024

Разность между показателями выборочной и генеральной совокупности называется ошибкой выборки . Ошибки выборки подразделяются на ошибки регистрации и ошибки репрезентативности.

Ошибки регистрации возникают из-за неправильных или неточных сведений. Источниками таких ошибок могут быть непонимание существа вопроса, невнимательность регистратора, пропуск или повторный счет некоторых единиц совокупности, описки при заполнении формуляров и т.д.

Расхождение между значениями изучаемого признака выборочной и генеральных совокупностей является ошибкой репрезентативности (представи-тельности). Она может быть случайной и систематической. Случайная возникает в силу того, что выборочное статистическое наблюдение является несплошным наблюдением, и выборка недостаточно точно воспроизводит (репрезентирует) генеральную совокупность.

Систематические ошибка репрезентативности возникают из-за неправильного, тенденциозного отбора единиц, при котором нарушается основной принцип научно организованной выборки - принцип случайности.

При определении величины репрезентативной ошибки предполагается, что ошибка регистрации равна нулю. Определение ошибки производится по формулам ошибки выборочной доли и ошибки выборочной средней . Систематическая ошибка репрезентативности возникает вследствие нарушения правил отбора единиц генеральной совокупности, в частности принципа беспристрастного, непреднамеренного отбора. Систематическая ошибка может привести к полной непригодности результатов наблюдений.

Рассмотрим на примере, насколько отличаются выборочные и генеральные показатели по данным об успеваемости студентов (две 10%-е выборки):

Если у вас возникли сложности с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой - мы готовы помочь.

1.3. Ошибки выборочного отбора
Разность между показателями выборочной и генеральной совокупности называется ошибкой выборки. Ошибки выборки подразделяются на ошибки регистрации и ошибки репрезентативности.

Среди ошибок регистрации выделяются систематические, обусловленные причинами, действующими в каком-то одном направлении и искажающими результаты работы (например, округление цифр, тяготение к полным пятеркам, десяткам и т.д.), и случайные,проявляющиеся в различных направлениях, уравновешивающие друг друга и лишь изредка дающие заметный суммарный итог.
Расхождение между значениями изучаемого признака выборочной и генеральных совокупностей является ошибкой репрезентативности (представи-тельности). Она может быть случайной и систематической. Случайная возникает в силу того, что выборочное статистическое наблюдение является несплошным наблюдением, и выборка недостаточно точно воспроизводит (репрезентирует) генеральную совокупность.
Систематические ошибка репрезентативности возникают из-за неправильного, тенденциозного отбора единиц, при котором нарушается основной принцип научно организованной выборки - принцип случайности.

При определении величины репрезентативной ошибки предполагается, что ошибка регистрации равна нулю. Определение ошибки производится по формулам ошибки выборочной доли и ошибки выборочной средней. Систематическая ошибка репрезентативности возникает вследствие нарушения правил отбора единиц генеральной совокупности, в частности принципа беспристрастного, непреднамеренного отбора. Систематическая ошибка может привести к полной непригодности результатов наблюдений.

Средний балл для генеральной совокупности

по первой выборке

по второй выборке

Доля студентов, получивших оценки "4" и "5":

по генеральной совокупности

по первой выборке

по второй выборке

Разность между показателями выборочной и генеральной совокупности является случайной ошибкой репрезентативности (ошибкой выборки).

Как видно из расчетов, выборочная средняя и выборочная доля являются случайными величинами, которые могут принимать различные значения в зависимости от того, какие единицы совокупности попали в выборку.
1.3.1. Ошибка выборочной средней
Ошибка выборочной средней представляет собой расхождение (разность) между выборочной средней и генеральной средней , возникающее вследствие несплошного выборочного характера наблюдения. Величина ошибки выборочной средней определяется как предел отклонения от , гарантируемый с заданной вероятностью:

где – гарантийный коэффициент, зависящий от вероятности , с которой гарантируется невыход разности за пределы ; – средняя ошибка выборочной средней.

Значения гарантийного коэффициента и соответствующие им вероятности приведены в табл.4.1. Обычно вероятность принимается равной 0,9545 или 0,9973, а при этом равно соответственно 2 и 3.

При правильном формировании выборки величину ее ошибки можно рассчитать заранее. В общем случае под ошибкой выборкипонимают объективно возникающее расхождение между характеристиками выборки и генеральной совокупности.

Ошибки выборкиподразделяются на ошибки регистрации и ошибки репрезентативности.

Ошибки регистрациивозникают из-за неправильных или неточных сведений. Их источником является невнимательность регистратора, неправильное заполнение формуляров, описки или же непонимание существа исследуемого вопроса.

Ошибки репрезентативностивозникают вследствие несоответствия структуры выборки структуре генеральной совокупности. Источником их существования является разная вариация признака у статистических единиц, в результате которой распределение единиц в выборочной совокупности отличается от распределения единиц в генеральной совокупности.

Ошибки репрезентативности делятся на систематические и случайные.

Систематические ошибкирепрезентативности возникают из-за неправильного формирования выборки, при котором нарушается основной принцип научно организованной выборки – принцип случайности.

Случайные ошибкирепрезентативности означают, что даже при соблюдении принципа случайности отбора единиц, расхождения между характеристиками выборки и генеральной совокупности все же имеют место.

Ошибка выборочного наблюдения – это разность между величиной параметра в генеральной совокупности и его величиной, вычисленной по результатам выборочного наблюдения. Для среднего значения ошибка будет определяться так:

х_i – вариант (значение варьирующего признака)

N – объем генеральной совокупности ( = сумме f_i)

х_i – вариант (значение варьирующего признака)

n – объем выборочной совокупности

Рассмотрим пример: Даны две 10-ти процентные выборки успеваемости студентов (табл. 6.1).

Таблица 6.1 – Исходные данные

Оценка	Число студентов
Генеральная совокупность	1-я выборка	2-я выборка
Итого:

Рассчитаем ошибку выборки.

1. Средний балл рассчитываем по средней арифметической взвешенной:

По генеральной совокупности:

По выборочным совокупностям:

Разность между показателями выборочной и генеральной совокупности и будет случайной ошибкой репрезентативности:

Величина ошибки выборки зависит от следующих факторов:

- Степени колеблемости признака в генеральной совокупности

Чем однороднее исследуемая совокупность, тем меньше величина средней ошибки при той же самой численности выборки.

- Объема (численности) выборки

Увеличивая или уменьшая объем выборки n, можно регулировать величину средней ошибки. Чем больше единиц будет включено в выборку, тем меньше будет величина ошибки, так как тем точнее в выборке будет представлена генеральная совокупность.

- Способа отбора единиц в выборочную совокупность

Для каждого способа формирования выборки величина ее ошибки определяется по разному. В практической деятельности используются различные способы формирования выборочной совокупности, но принципиальное значение имеет их деление на способы случайного (повторного и бесповторного) отбора.

При собственно случайном повторном отбореобщее число единиц генеральной совокупности в процессе выборке не меняется.

Статистическая единица, попавшая в выборку, после регистрации изучаемого признака возвращается в генеральную совокупность и можетвновь попасть в выборку. Таким образом, для всех единиц генеральнойсовокупности обеспечивается равная вероятность отбора.

В математической статистике доказывается, что средняя ошибка выборки определяется по формуле: (6.3)

где - дисперсия генеральной совокупности;

n – объем выборочной совокупности.

Дисперсия – отклонение признака от средней величины. Генеральная дисперсия, также как и остальные параметры генеральной совокупности, является неизвестной величиной, но известно соотношение между генеральной и выборочной дисперсией: ~ , тогда при достаточно большом объеме выборки (n>30), является величиной близкой к 1, и можно считать, что ~ . В случаях малой выборки при n

Повторная и бесповторная выборка. Что это значит? Слова говорят сами за себя:

– Если случайно отбираемые объекты не возвращаются в генеральную совокупность, то это бесповторная выборка. Если же выбранный объект возвращается обратно (перед выбором следующего), то это повторная выборка, т.е. здесь один и тот же попугай может быть выбран неоднократно.

А теперь к теме. На данном уроке мы рассмотрим детализированную задачу о доверительном интервале генеральной средней и о доверительном интервале доли; последняя только что встретилась в предновогодней статье об оценке вероятности биномиального распределения (Пример 29). Детализация состоит в том, что построение доверительного интервала зависит от того, бесповторная была проведена выборка или повторная. Как и прежде, полагаем, что во всех нижеследующих задачах генеральная совокупность распределена нормально, либо её распределение близкО к таковому. Этот факт может быть известен и / или подкреплён статистическими методами.

Для опытных читателей мини-оглавление и быстрая ссылка:

Оценка генеральной средней (заголовок ниже)
Оценка генеральной доли

и для всех – большой и приятный путь:

Оценка генеральной средней

Итак, записываем: пусть из нормально распределенной (или около того) генеральной совокупности объёма проведена выборка объёма и по её результатам найдена выборочная средняя и исправленная выборочная дисперсия .

Если объём выборки , то коэффициент доверия определяется с помощью распределения Стьюдента (см. также Пункт 11б для ). Если , то чаще пользуются соотношением , где – функция Лапласа, а – доверительная вероятность. Если известна генеральная дисперсия, то второй вариант.

С конспектом отмучились, теперь задачи :) Есть у меня тут на выбор несколько штук: про вклады в банке, про токарей на заводе, …но, вот, пожалуй, самая зимняя – как говорится, у кого подснежники в марте, а у кого и подсолнухи в декабре:)

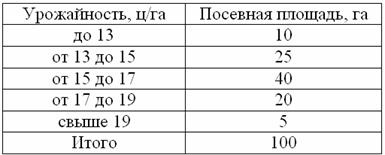
С целью изучения урожайности подсолнечника в колхозах области проведено 5%-ное выборочное обследование 100 га посевов, отобранных в случайном порядке, в результате которого получены следующие данные:

С вероятностью 0,9973 определить предельную ошибку выборки и возможные границы, в которых ожидается средняя урожайность подсолнечника в области.

Решение: в условии не указан тип отбора, но исходя из логики исследования, положим, что он бесповторный. Поскольку выборка 5%-ная, то она составляет 1/20-ю часть генеральной совокупности, стало быть, общая посевная площадь области составляет:
гектаров – не знаю, насколько это реалистично, оставим этот вопрос на совести автора задачи.

По условию, требуется найти предельную ошибку выборки , где – коэффициент доверия, соответствующий доверительной вероятности , и коль скоро выборка бесповторна и генеральной дисперсии мы не знаем, то средняя ошибка рассчитывается по формуле . Далее нужно найти интервал , который с вероятностью 99,73% накроет генеральную среднюю урожайность подсолнечника по области.

Смотрим на таблицу выше и приходим к выводу, что нам предложен интервальный вариационный ряд с открытыми крайними интервалами. Поскольку длина частичного интервала составляет га, то вопрос закрываем так: 11-13 и 19-21 га.

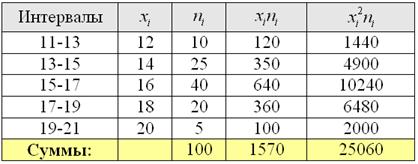
Находим середины интервалов (переходим к дискретному ряду), произведения и их суммы:

С порядком заполнения таблицы и техникой вычислений можно ознакомиться на предыдущих уроках, даже кино на эту тему есть.

Вычислим выборочную среднюю:
– центнеров с гектара.

Выборочную дисперсию вычислим по формуле:

Этим частенько пренебрегают, но я призываю поправлять дисперсию:
– мелочь, а приятно.

И составляем доверительный интервал для оценки генеральной средней урожайности подсолнечника по области.

Вычислим предельную ошибку .

Так как объём выборки , то коэффициент доверия ищем из соотношения (но можно использовать и распределение Стьюдента). Поскольку , то:

По таблице значений функции Лапласа или с помощью Экселя (Пункт 5*), определяем, что этому значению функции соотвествует аргумент .

Вычислим среднюю ошибку бесповторной выборки:
ц/га, таким образом, предельная ошибка составляет ц/га, и искомый доверительный интервал:

(ц/га) – границы, в которых ожидается средняя урожайность подсолнечника в области с вероятностью .

Ответ: ц/га, (ц/га)

Теперь распишем интервал в развёрнутом виде:

и проанализируем дробь . Очевидно, что при увеличении объёма выборки эта дробь будут увеличиваться до единицы, и, соответственно, разность будет уменьшаться до нуля. Таким образом, предельная ошибка уменьшается, и доверительный интервал становится меньше, что вполне логично – ведь чем больше выборка, тем точнее оценка. И в предельном случае, когда мы исследовали всю генеральную совокупность , ошибка становится нулевой и доверительный интервал вырождается в генеральную среднюю .

Исходя из вышесказанного, можно рассмотреть две обратные задачи:

1) Предположим, что нам хочется уменьшить доверительный интервал, например, в два раза, т.е. споловинить предельную ошибку до ц/га (вместо 0,6). Но высокую доверительную вероятность и соответствующий коэффициент мы сохранить хотим. Тогда ничего не остаётся, как увеличивать объём выборки. Из соотношения выведем формулу для нахождения этого объёма, для этого возведём обе части в квадрат:
и разрешим уравнение относительно :
, откуда следует:

Таким образом, для того чтобы с доверительной вероятностью обеспечить точность , следует организовать выборку объёмом:

гектара – округляем в бОльшую сторону, что составляет генеральной совокупности. Таким образом, трудозатраты возросли примерно в 3,5 раза. Тоже логично.

2) Теперь обратная ситуация – когда оценка нас устраивают, но нет возможности или времени проводить большую выборку. Да чего тут, исследовали гектаров из , и нормально. В этом случае пострадает доверительная вероятность, давайте выясним насколько:

и с помощью расчётного макета (Пункт 11а) для количества степеней свободы находим соответствующую доверительную вероятность:

Впрочем, это было очевидно – ведь такая малая выборка явно не репрезентативна (плохо представляет генеральную совокупность).

Поэтому нужно найти возможность, время, желание и провести нормальное исследование :) А также решить следующую задачу:

По результатам 10%-ной бесповторной выборки объёма , найдены выборочная средняя и дисперсия .

а) Найти пределы, за которые с доверительной вероятностью 0,954 не выйдет среднее значение генеральной совокупности.

б) Выборку примерно какого объёма нужно организовать, чтобы с той же доверительной вероятностью улучшить точность оценки в три раза?

Краткое решение и ответ в конце урока.

Если выборка повторная, то почти всё то же самое, с той поправкой, что средняя ошибка выборки определяется без множителя :
, таким образом, предельная ошибка составляет и соответствующий доверительный интервал для оценки генеральной средней:
– не что иное, как интервал, который был рассмотрен и неоднократно построен в 1-й части урока о статистических оценках.

Примечание: если известна дисперсия генеральной совокупности , то, разумеется, используется она.

Теперь поставим предельные ошибки рядом:

и проанализируем такой момент: при большом объёме генеральной совокупности (которая может быть и бесконечной) и малом объёма выборки грань между формулами стирается. По той причине, что дробь стремится к нулю и разность – к единице, в результате чего 1-я формула практически совпадает со 2-й, чем мы уже пользовались ранее. Вспомним, например, Пример 21:

“
Известно, что генеральная совокупность распределена нормально со средним квадратическим отклонением . Найти доверительный интервал для оценки математического ожидания с надежностью 0,95, если выборочная средняя , а объем выборки .
”

В условии не сказано, повторная ли проведена выборка или бесповторная, и не известен объём генеральной совокупности. Поэтому ничего не остаётся, как допустить, что она очень великА и пользоваться формулой . В том решении мы получили и доверительный интервал , который с вероятностью накрывает неизвестное математическое ожидание . Кроме того, было прорешано ещё несколько похожих задач, но во всех из них остался за кадром анализ объёма выборки. И сейчас пришло время наверстать упущенное:

По данным Примера 21 () определить объём выборки, обеспечивающий точность с вероятностью .

Да, вот так вот сурово :)

Доверительной вероятности соответствует коэффициент (из соотношения ).

Таким образом:
– объём выборки, необходимый для обеспечения точности с вероятностью .

Это означает, что доверительный интервал , где – значение, найденное по выборке объёмом 900, практически достоверно накроет генеральную среднюю .

И ещё раз подчёркиваю, что значение из Примера 21 использовать нельзя, ибо новая выборка – новая средняя. Но заметьте, что здесь известна генеральная дисперсия и поэтому точность будет выдержана строго.

Ответ:

Как видите, объём заметно возрос, и если вам хочется совсем крутой точности, скажем, с той же вероятностью , то придётся выбрать уже:
объектов, после чего практически достоверно можно утверждать, что рассчитанное по этой выборке значение будет отличаться от менее чем на 0,1. Но тут нужно смотреть – будет ли такая большая выборка целесообразной.

И в заключение параграфа ещё один любопытный факт: если для бесповторной выборки ошибка может строго равняться нуля (когда ), то для повторной выборки это не так: – здесь она может лишь стремиться к нулю при , даже если объём генеральной совокупности конечен. Это обусловлено эффектом повторности – представьте, что из чёрного ящика наугад извлекаются некие предметы и возвращаются обратно. Мало того, что они будут учтены не одинаковое количество раз, так некоторые из них теоретически могут вообще не попадаться сколь угодно долго.

Оценка генеральной доли

Быстренько освежим в памяти, что такое доля. Пусть из генеральной совокупности объёма вновь проведена выборка объёмом , и по её результатам требуется оценить генеральную долю объектов, обладающих некоторым количественным или качественным признаком.

Вспоминаем помидоров на базе, среди которых первосортных. Тогда отношение является генеральной долей первосортных помидоров. Однако исследовать все овощи затруднительно, поэтому организуется представительная выборка из помидоров, среди которых первосортных окажется штук. Отношение называется выборочной долей.

И наша задача состоит в том, чтобы по найденному значению оценить истинную долю . Как оценить? С помощью доверительного интервала:
, где – предельная ошибка доли.

Далее для удобства я буду опускать подстрочный индекс у выборочной доли: .

В том случае, если выборка достаточно велика ( порядка сотни и больше), а доля не слишком малА (по крайне мере, больше нескольких процентов), то предельная ошибка доли определяется как произведение , где – коэффициент доверия, определяемый из того же соотношения для заданного уровня доверительной вероятности, а – средняя ошибка доли, которая определяется так:
– для бесповторной выборки;
– для повторной выборки.

В том случае, если генеральная совокупность велика, а выборка малА, то для бесповторной выборки можно использовать и 2-ю формулу, ибо дробь будет близка к нулю.

Как видите, формулы очень похожи, только вместо дисперсии у нас тут произведение , и чего томиться, сразу задача:

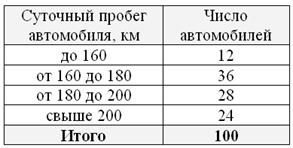
В целях изучения суточного пробега автомобилей автотранспортного предприятия проведено 10%-ное выборочное обследование 100 автомобилей методом случайного бесповторного отбора, в результате которого получены следующие данные:

С вероятностью 0,954 требуется определить долю машин в генеральной совокупности с пробегом более 180 км.

Решение: вычислим количество автомобилей с пробегом более 180 км по выборке:
. Таким образом:
– выборочная доля автомобилей с пробегом более 180 километров.

Генеральную долю таких автомобилей оценим с помощью доверительного интервала:
, где – предельная ошибка доли.

Для уровня доверительной вероятности находим знакомый коэффициент доверия:

Вычислим среднюю ошибку доли. Коль скоро выборка 10%-ная, то объём генеральной совокупности равен автомобилей и для бесповторной выборки:

Таким образом, предельная ошибка доли и искомый доверительный интервал:

– с вероятностью 95,4% данный интервал накрывает истинную генеральную долю автомобилей с пробегом более 180 км.

Ответ:

Кстати, тут можно оценить и абсолютное количество таковых машин:

– от 425 до 615 автомобилей.

Но результат, конечно, такой слабоватый. И помочь здесь может увеличение выборки.
Родственная формула уже выведена в предыдущем параграфе, и я просто заменю дисперсию произведением :
– здесь по желаемой предельной ошибке можно вычислить необходимый объём выборки.

И прямо сейчас у вас представится такая возможность. На десерт:

Методом механического отбора проведено однопроцентное обследование веса пирожных, изготовленных кондитерской фабрикой за сутки. Распределение веса пирожных по весу следующее:

а) С вероятностью 0,9973 определить пределы, в которых будет находиться доля пирожных весом не менее 100 г, во всей суточной продукции

б) Сколько процентов пирожных нужно проверить, чтобы улучшить оценку в 7 раз? (при той же доверительной вероятности)

Краткое решение и ответ в конце урока. И в его заключение пара слов о повторной выборке. На самом деле такую задачу мы уже разобрали на уроке об оценке вероятности биномиального распределения (Пример 29). Цитирую условие:

“
Проверив изделий, обнаружили, что изделий высшего сорта. Сколько надо проверить изделий, чтобы с уверенностью 95% определить долю высшего сорта с точностью до 0,01?
”

Заметьте, что в этой задаче ничего не сказано о типе выборки, но, судя по всему, она бесповторна. Однако размер генеральной совокупности не указан, и поэтому ничего не остаётся, как предположить, что изделий очень много и использовать формулу повторной выборки.

С решением можно ознакомиться по ссылке выше (единственное, там буквы немного другие), ну а я ещё раз поздравляю всех с праздником – всем солнца, пирожных и автомобилей! И, конечно, хороших оценок ;)

Решения и ответы:

Пример 31. Решение: вычислим исправленную выборочную дисперсию:

а) Вычислим предельную ошибку выборки.
Так как , то коэффициент доверия найдём из соотношения .

Примечание: ввиду небольшого объёма выборки хорошо смотрится и оценка по Стьюденту, что может быть даже предпочтительнее.

По условию, , следовательно:

По таблице значений функции Лапласа находим, что этому значению функции соотвествует аргумент

Поскольку выборка 10%-ная бесповторная, то объём генеральной совокупности равен:

Вычислим среднюю ошибку выборки:

Таким образом, предельная ошибка:
и искомый доверительный интервал:

– пределы, которые с доверительной вероятностью 0,954 накрывают среднее значение генеральной совокупности.

б) Улучшим точность оценки в три раза: и воспользуемся формулой:
(округлять лучше до бОльшего значения)

Таким образом, для того, чтобы с вероятностью 95,4% утверждать, что отличается от менее чем на , следует провести выборку объёмом примерно (что составляет половину генеральной совокупности, и, конечно, нецелесообразно).

Пример 34. Решение:

а) Вычислим количество пирожных весом не менее 100 грамм:
. Таким образом:
– выборочная доля таковых пирожных.

Соответствующую генеральную долю оценим с помощью доверительного интервала:
, где – предельная ошибка.

Уровню доверительной вероятности соответствует коэффициент
Вычислим среднюю ошибку доли. Поскольку выборка 1%-ная и бесповторная, то:

Таким образом, предельная ошибка доли и искомый доверительный интервал:

– данный интервал практически достоверно накрывает долю пирожных весом не менее 100 грамм во всей суточной партии.

б) Улучшим точность оценки в 7 раз: и вычислим объём выборки, которую следует организовать, чтобы обеспечить эту точность. Учитывая, что объём генеральной совокупности составляет :

Таким образом, для того, чтобы с вероятностью 99,73% можно было утверждать, что выборочная доля пирожных весом не менее 100 грамм будет отличаться от истинного значения менее чем на 0,02, следует организовать выборку объёмом пирожных, что составляет примерно треть генеральной совокупности.

Автор: Емелин Александр

(Переход на главную страницу)

cкидкa 15% на первый зaкaз, при оформлении введите прoмoкoд: 5530-hihi5

Читайте также: