Правило трех сигм реферат

Обновлено: 05.07.2024

Пределы трех сигм – это статистический расчет, при котором данные находятся в пределах трех стандартных отклонений от среднего . В бизнес-приложениях три сигмы относятся к процессам, которые работают эффективно и производят изделия высочайшего качества.

Пределы трех сигм используются для установки верхнего и нижнего контрольных пределов в диаграммах статистического контроля качества . Контрольные диаграммы используются для установления пределов для производственного или бизнес-процесса, который находится в состоянии статистического контроля.

Ключевые моменты:

Пределы трех сигм (пределы трех сигм) – это статистический расчет, который относится к данным в пределах трех стандартных отклонений от среднего.
Пределы трех сигм используются для установки верхнего и нижнего контрольных пределов в диаграммах статистического контроля качества.
На кривой колокола данные, которые лежат выше среднего и за линией трех сигм, представляют менее 1% всех точек данных.

Понимание пределов трех сигм

Контрольные диаграммы также известны как диаграммы Шухарта, названные в честь Уолтера А. Шухарта, американского физика, инженера и статистика (1891–1967).1 Контрольные диаграммы основаны на теории, согласно которой даже в идеально спроектированных процессах существует определенная вариативность выходные измерения присущи.

Контрольные диаграммы определяют, есть ли в процессе контролируемое или неконтролируемое изменение. Считается, что отклонения в качестве процесса по случайным причинам находятся под контролем; Неконтролируемые процессы включают как случайные, так и особые причины отклонений. Контрольные карты предназначены для определения наличия особых причин.

Для измерения вариаций статистики и аналитики используют показатель, известный как стандартное отклонение, также называемый сигмой. Сигма – это статистическое измерение изменчивости, показывающее, насколько существует отклонение от среднего статистического значения.

Краткая справка

Сигма измеряет, насколько наблюдаемые данные отклоняются от среднего или среднего значения; инвесторы используют стандартное отклонение для измерения ожидаемой волатильности, известной как историческая волатильность.

Чтобы понять это измерение, рассмотрим нормальную кривую колокола , которая имеет нормальное распределение. Чем дальше вправо или влево точка данных записывается на колоколообразной кривой, тем выше или ниже, соответственно, данные, чем среднее значение. С другой стороны, низкие значения указывают на то, что точки данных близки к среднему; высокие значения указывают на то, что данные широко распространены и не близки к среднему.

Пример расчета предела трех сигм

Давайте рассмотрим производственную фирму, которая проводит серию из 10 тестов, чтобы определить, есть ли различия в качестве ее продукции. Точки данных для 10 тестов: 8,4, 8,5, 9,1, 9,3, 9,4, 9,5, 9,7, 9,7, 9,9 и 9,9.

Сначала рассчитайте среднее значение наблюдаемых данных. (8,4 + 8,5 + 9,1 + 9,3 + 9,4 + 9,5 + 9,7 + 9,7 + 9,9 + 9,9) / 10, что равно 93,4 / 10 = 9,34.
Во-вторых, рассчитайте дисперсию набора. Дисперсия – это разброс между точками данных, который рассчитывается как сумма квадратов разницы между каждой точкой данных и средним значением, деленная на количество наблюдений. Первый квадрат разницы будет рассчитан как (8,4 – 9,34) 2 = 0,8836, второй квадрат разности будет (8,5 – 9,34) 2 = 0,7056, третий квадрат может быть рассчитан как (9,1 – 9,34) 2 = 0,0576, и скоро. Сумма различных квадратов всех 10 точек данных составляет 2,564. Таким образом, дисперсия составляет 2,564 / 10 = 0,2564.
В-третьих, вычислите стандартное отклонение, которое представляет собой просто квадратный корень из дисперсии. Итак, стандартное отклонение = √0,2564 = 0,5064.
В-четвертых, вычислите три сигмы, что на три стандартных отклонения выше среднего. В числовом формате это (3 x 0,5064) + 9,34 = 10,9. Поскольку ни один из данных не находится на таком высоком уровне, процесс производственных испытаний еще не достиг уровня качества трех сигм.

Особые соображения

Поскольку около 99,99% управляемого процесса будет происходить в пределах плюс-минус трех сигм, данные процесса должны приблизительно соответствовать общему распределению вокруг среднего значения и в заранее определенных пределах. На кривой колокола данные, которые лежат выше среднего и за линией трех сигм, представляют менее 1% всех точек данных.

При рассмотрении нормального закона распределения выделяется важный частный случай, известный как правило трех сигм.

Запишем вероятность того, что отклонение нормально распределенной случайной величины от математического ожидания меньше заданной величины D:

Если принять D = 3s, то получаем с использованием таблиц значений функции Лапласа:

Т.е. вероятность того, что случайная величина отклонится от своего математического ожидание на величину, большую чем утроенное среднее квадратичное отклонение, практически равна нулю.

Это правило называется правилом трех сигм.

Не практике считается, что если для какой – либо случайной величины выполняется правило трех сигм, то эта случайная величина имеет нормальное распределение.

Пример . Поезд состоит из 100 вагонов. Масса каждого вагона – случайная величина, распределенная по нормальному закону с математическим ожидание а = 65 т и средним квадратичным отклонением s = 0,9 т. Локомотив может везти состав массой не более 6600 т, в противном случае необходимо прицеплять второй локомотив. Найти вероятность того, что второй локомотив не потребуется.

Второй локомотив не потребуется, если отклонение массы состава от ожидаемого (100×65 = 6500) не превосходит 6600 – 6500 = 100 т.

Т.к. масса каждого вагона имеет нормальное распределение, то и масса всего состава тоже будет распределена нормально.

Получаем:

Пример . Нормально распределенная случайная величина Х задана своими параметрами – а = 2 – математическое ожидание и s = 1 – среднее квадратическое отклонение. Требуется написать плотность вероятности и построить ее график, найти вероятность того, Х примет значение из интервала (1; 3), найти вероятность того, что Х отклонится (по модулю) от математического ожидания не более чем на 2.

Плотность распределения имеет вид:

Построим график:

Найдем вероятность попадания случайной величины в интервал (1; 3).

Найдем вероятность отклонение случайной величины от математического ожидания на величину, не большую чем 2.

Тот же результат может быть получен с использованием нормированной функции Лапласа.

Центральная предельная теорема Ляпунова

Теорема . Если случайная величина Х представляет собой сумму очень большого числа взаимно независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, то Х имеет распределение, близкое к нормальному.

На практике для большинства случайных величин выполняются условия теоремы Ляпунова.

Если известна плотность распределения, то функция распределения может быть легко найдена по формуле:

Двумерная плотность распределения неотрицательна и двойной интеграл с бесконечными пределами от двумерной плотности равен единице.

По известной плотности совместного распределения можно найти плотности распределения каждой из составляющих двумерной случайной величины.

Условные законы распределения

Как было показано выше, зная совместный закон распределения можно легко найти законы распределения каждой случайной величины, входящей в систему.

Однако, на практике чаще стоит обратная задача – по известным законам распределения случайных величин найти их совместный закон распределения.

В общем случае эта задача является неразрешимой, т.к. закон распределения случайной величины ничего не говорит о связи этой величины с другими случайными величинами.

Кроме того, если случайные величины зависимы между собой, то закон распределения не может быть выражен через законы распределения составляющих, т.к. должен устанавливать связь между составляющими.

Все это приводит к необходимости рассмотрения условных законов распределения.

Определение . Распределение одной случайной величины, входящей в систему, найденное при условии, что другая случайная величина приняла определенное значение, называется условным законом распределения.

Условный закон распределения можно задавать как функцией распределения так и плотностью распределения.

Условная плотность распределения вычисляется по формулам:

Условная плотность распределения обладает всеми свойствами плотности распределения одной случайной величины.

Условное математическое ожидание

Определение . Условным математическим ожиданием дискретной случайной величины Y при X = x (х – определенное возможное значение Х) называется произведение всех возможных значений Y на их условные вероятности.

Для непрерывных случайных величин:

где f(y/x) – условная плотность случайной величины Y при X=x.

Условное математическое ожидание M(Y/x)=f(x) является функцией от х и называется функцией регрессии Х на Y.

Пример . Найти условное математическое ожидание составляющей Y при

X = x₁ = 1 для дискретной двумерной случайной величины, заданной таблицей:

Y	X
x₁=1	x₂=3	x₃=4	x₄=8
y₁=3	0,15	0,06	0,25	0,04
y₂=6	0,30	0,10	0,03	0,07

Аналогично определяются условная дисперсия и условные моменты системы случайных величин

Зависимые и независимые случайные величины

Случайные величины называются независимыми, если закон распределения одной из них не зависит от того какое значение принимает другая случайная величина.

Понятие зависимости случайных величин является очень важным в теории вероятностей.

Условные распределения независимых случайных величин равны их безусловным распределениям.

Определим необходимые и достаточные условия независимости случайных величин.

Теорема . Для того, чтобы случайные величины Х и Y были независимы, необходимо и достаточно, чтобы функция распределения системы (X, Y) была равна произведению функций распределения составляющих.

Аналогичную теорему можно сформулировать и для плотности распределения:

Теорема . Для того, чтобы случайные величины Х и Y были независимы, необходимо и достаточно, чтобы плотность совместного распределения системы (X, Y) была равна произведению плотностей распределения составляющих.

Определение . Корреляционным моментом m_xy случайных величин Х и Y называется математическое ожидание произведения отклонений этих величин.

Практически используются формулы:

Для дискретных случайных величин:

Для непрерывных случайных величин:

Корреляционный момент служит для того, чтобы охарактеризовать связь между случайными величинами. Если случайные величины независимы, то их корреляционный момент равен нулю.

Корреляционный момент имеет размерность, равную произведению размерностей случайных величин Х и Y. Этот факт является недостатком этой числовой характеристики, т.к. при различных единицах измерения получаются различные корреляционные моменты, что затрудняет сравнение корреляционных моментов различных случайных величин.

Для того, чтобы устранить этот недостаток применятся другая характеристика – коэффициент корреляции.

Определение . Коэффициентом корреляции r_xy случайных величин Х и Y называется отношение корреляционного момента к произведению средних квадратических отклонений этих величин.

Коэффициент корреляции является безразмерной величиной. Коэффициент корреляции независимых случайных величин равен нулю.

Свойство : Абсолютная величина корреляционного момента двух случайных величин Х и Y не превышает среднего геометрического их дисперсий.

Свойство : Абсолютная величина коэффициента корреляции не превышает единицы.

Случайные величины называются коррелированными, если их корреляционный момент отличен от нуля, и некоррелированными, если их корреляционный момент равен нулю.

Если случайные величины независимы, то они и некоррелированы, но из некоррелированности нельзя сделать вывод о их независимости.

Если две величины зависимы, то они могут быть как коррелированными, так и некоррелированными.

Часто по заданной плотности распределения системы случайных величин можно определить зависимость или независимость этих величин.

Наряду с коэффициентом корреляции степень зависимости случайных величин можно охарактеризовать и другой величиной, которая называется коэффициентом ковариации. Коэффициент ковариации определяется формулой:

Пример . Задана плотность распределения системы случайных величин Х и Y.

Выяснить являются ли независимыми случайные величины Х и Y.

Для решения этой задачи преобразуем плотность распределения:

В чем заключается правило трех сигм (3-sigma rule) в статистике

Математическое ожидание — это среднее значение случайной величины. Обозначается как $\mu$ .

Правило трех сигм заключается в том, что при нормальном распределении практически все значения величины с вероятностью 0,9973 лежат не далее трех сигм в любую сторону от математического ожидания, то есть находятся в диапазоне $\left[\mu-3\sigma;\;\mu+3\sigma\right]$ .

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Приблизительно 99,7% всех значений лежат в пределе трех сигм от математического ожидания, около 95% — в пределах двух сигм, а примерно 68% значений лежат в пределах всего одной сигмы.

Те значения, которые выходят за рамки 3 сигм, принято считать грубыми ошибками. Большое количество таких ошибок может свидетельствовать о том, что распределение на самом деле не является нормальным. В этом заключается практическая польза правила 3 сигм.

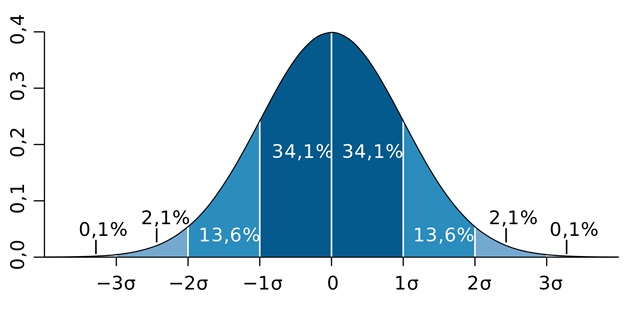
Нормальное распределение случайной величины

Нормальное распределение (распределение Гаусса) — это такое распределение вероятностей, функция плотности которого совпадает с функцией Гаусса.

где $\mu$ — значение математического ожидания, $\sigma$ – величина среднеквадратического отклонения, $\sigma^2$ — дисперсия распределения.

Функция плотности — это функция, которая характеризует сравнительную вероятность реализации определенных значений случайной переменной или переменных.

Нормальное распределение величины центрировано и нормировано.

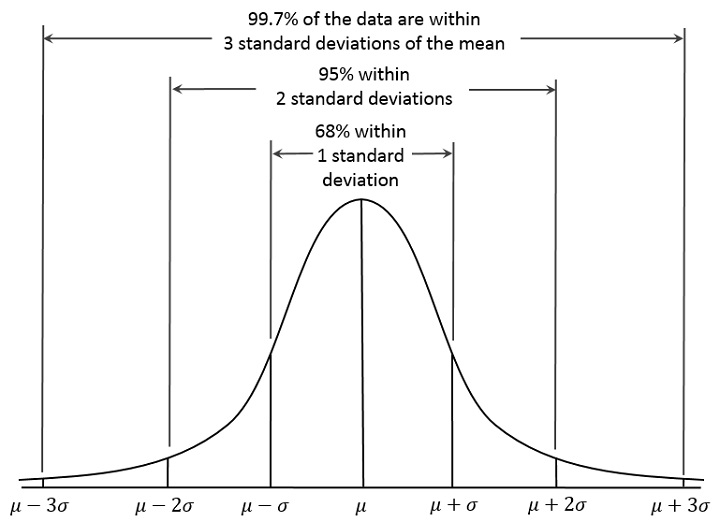
График нормального распределения тесно связан с центральной предельной теоремой (ЦПТ). Согласно ЦПТ, сумма достаточно большого количества слабо зависимых случайных величин имеет распределение, близкое к нормальному.

Нормальное распределение не является абстрактным понятием. Ему соответствуют некоторые характеристики живых организмов в популяции, отклонение от мишени при стрельбе, измерения и их погрешности. Во всех этих случаях наиболее распространена группа близких значений, но есть отклонения как в большую, так и в меньшую сторону.

Примеры решения задач

Рассмотрим несколько простых задач на применение правила 3 сигм.

Задача 1

Имеется выборка жителей богатого дома. Средняя зарплата жильцов составляет 150 000 рублей, среднеквадратичное отклонение равно 20 000 рублей. Определите, жители с какой зарплатой вряд ли могут жить в этом доме: А) 205 000 рублей; Б) 95 000; В) 230 000; Г) 87 000.

Решение

Чтобы решить данную задачу, необходимо определить, каковы верхние и нижние границы возможных зарплат в доме. Для этого воспользуемся правилом 3 сигм.

Значения А, Б входят в диапазон $\left[90\;000;\;210\;000\right]$ . Значения В, Г не входят в него и, следовательно, являются искомыми грубыми ошибками.

Задача 2

Завод выпускает партии по 100 цилиндрических деталей. Диаметр каждой детали — случайная величина, распределенная по нормальному закону. Математическое ожидание равно 65 мм, а среднее отклонение составляет 0,9 мм. Для упаковки партии используют коробки шириной 6600 мм. Детали кладут в один ряд. Если детали не поместятся в одну коробку, придется брать еще одну. Найдите вероятность, что понадобится только одна коробка.

Решение

Т. к. диаметр каждой детали распределен нормально, то и их общий диаметр также будет распределен нормально.

Чтобы все детали поместились в одну коробку, необходимо, чтобы отклонение диаметра всех деталей отклонялось от ожидаемого не более чем на 100 мм. Это следует из того, что математическое ожидание общего диаметра всех деталей равно $65\cdot100=6500$ . А ширина коробки составляет 6600 мм.

Для расчета воспользуемся формулами дисперсии и правилом 3 сигм, чтобы вычислить вероятность, что понадобится только одна коробка.

ГОСТ

Напомним для начала следующие факты:

Вспомним формулу для нахождения вероятности того, что отклонение, распределенной по нормальному закону непрерывной случайной величины $X$, от математического ожидания $a$ по абсолютной величине (то есть по модулю) будет меньше $\delta $:

Напомним таблицу нахождения значений интегральной функции (таблица 1)

Рисунок 1. Значения интегральной функции $Ф(x)$.

Теперь найдем, чему будет равна вероятность того, что отклонение, распределенной по нормальному закону непрерывной случайной величины $X$, от математического ожидания $a$ по абсолютной величине (то есть по модулю) будет меньше $3\sigma $, то есть:

Геометрически этот факт можно представить следующим образом:

Из всего вышесказанного сформулируем следующее правило:

Правило трёх сигм: Если непрерывная случайная величина $X$ распределена по нормальному закону, то абсолютная величина её отклонения от математического ожидания $a$ не превосходит утроенного значения среднего квадратического отклонения $\sigma $.

Примеры решения задач на применение правила трех сигм

Длина изготавливаемого стержня подчинена нормальному закону распределения. Математическое ожидание $a=1$ м, а среднее математическое отклонение $\sigma =0,01$ м. Найти границы, пределах которых гарантируется длина стержня.

Для решения задачи воспользуемся правилом трех сигм:

Текущая цена на молоко подчинена нормальному закону распределения. Математическое ожидание $a=25$ рублей, а среднее математическое отклонение $\sigma =1$ рубль. Найти границы, в которых будет находиться текущая цена нам молоко.

Для решения задачи воспользуемся правилом трех сигм:

\[P\left(|X-a|Так как случайная величина (цена) распределена по нормальному закону, то \[P\left(\left|X-25\right|Ответ: (22,28).

На заводе изготавливают шурупы для ноутбуков. Размер диаметра шурупа распределен по нормальному закону распределения с математическим ожиданием $a=0,2\ $см и средним квадратическим отклонением $\sigma =0,02$ мм. В каких границах можно практически 100\% гарантировать размер шурупа?

Вначале приведем все величины к одному измерению:

Так как случайная величина подчинена нормальному закону распределения, то мы можем применить правило трех сигм:

Генеральная совокупность - множество всех объектов, относительно которых предполагается делать выводы при изучении конкретной задачи.

Выборка - часть генеральной совокупности, которая охватывается экспериментом.

Репрезентативная выборка - выборка, в которой все основные признаки генеральной совокупности, из которой извлечена данная выборка, представлены приблизительно в той же пропорции или с той же частотой, с которой данный признак выступает в этой генеральной совокупности.

Унимодальное распределение - распределение, имеющее только одну моду (пример: нормальное распределение)

Способы формирования репрезентативной выборки:

Простая случайная выборка (simple random sample)

Стратифицированная выборка (stratified sample)

Групповая выборка (cluster sample)

Типы переменных:

непрерывные (рост в мм)

дискретные (количество публикаций у учёного)

Ранговые (успеваемость студентов)

Гистограмма частот:

Позволяет сделать первое впечатление о форме распределения некоторого количественного признака.

Описательные статистики:

Меры центральной тенденции (узкий диапазон, высокие значения признака):

Мода (mode) - значение во множестве наблюдений, которое встречается наиболее часто.

Медиана (median) - значение признака, которое делит упорядоченное множество пополам.

Среднее значение (mean, среднее арифметическое) - сумма всех значений измеренного признака, делённая на количество измеренных значений.

( используется для среднего значения из выборки, а для генеральной совокупности латинская буква )

Свойства среднего:

Если к каждому значению выборки прибавить определённое число, то и среднее значение увеличится на это число.

Если каждое значение выборки умножить на определённое число, то и среднее значение увеличится в это число раз.

Если для каждого значения выборки, рассчитать такой показатель как его отклонение от среднего арифметического, то сумма этих отклонений будет равняться нулю.

Меры изменчивости (широкий диапазон, вариативность признака):

Размах (range) - разность максимального и минимального значения.

При добавлении сильно отличающегося значения данные меняются сильно и могут быть некорректные.

Дисперсия (variance) - средний квадрат отклонений индивидуальных значений признака от их средней величины.

Дисперсия генеральной совокупности:

(среднеквадратическое отклонение генеральной совокупности)

(среднеквадратическое отклонение выборки)

Свойства дисперсии:

Квартили распределения и график box-plot

Квартили - три точки (значения признака), которые делят упорядоченное множество данных на четыре равные части.

Box-plot - такой вид диаграммы в удобной форме показывает медиану (или, если нужно, среднее), нижний и верхний квартили, минимальное и максимальное значение выборки и выбросы.

Нормальное распределение

Отклонения наблюдений от среднего подчиняются определённому вероятностному закону.

Стандартизация

Стандартизация или z-преобразование - преобразование полученных данных в стандартную Z-шкалу (Z-scores) со средним и

Правило "двух" и "трёх" сигм

Центральная предельная теорема

Центральная предельная теорема - класс теорем в теории вероятностей, утверждающих, что сумма большого количества независимых случайных величин имеет распределение близкое к нормальному. Так как многие случайные величины в приложениях являются суммами нескольких случайных факторов, центральные предельные теоремы обосновывают популярность нормального распределения.

Есть признак, распределенный КАК УГОДНО* с некоторым средним и некоторым стандартным отклонением. Тогда, если выбирать из этой совокупности выборки объема n, то их средние тоже будут распределены нормально со средним равным среднему признака в ГС и стандартным отклонением .

Стандартная ошибка среднего - теоретическое стандартное отклонение всех средних выборки размера , извлекаемое из совокупности.

Доверительные интервалы для среднего

Доверительный интервал является показателем точности измерений. Это также показатель того, насколько стабильна полученная величина, то есть насколько близкую величину (к первоначальной величине) вы получите при повторении измерений (эксперимента).

Идея статистического вывода

P-значение (P-value) - величина, используемая при тестировании статистических гипотез. Фактически это вероятность ошибки при отклонении нулевой гипотезы (ошибки первого рода).

2. Сравнение средних

T-распределение

Если число наблюдений невелико и \sigma неизвестно (почти всегда), используется распределение Стьюдента (t-distribution).

Унимодально и симметрично, но: наблюдения с большей вероятностью попадают за пределы от

"Форма" распределения определяется числом степеней свободы ().

С увеличением числа распределение стремится к нормальному.

t-распределение используется не потому что у нас маленькие выборки, а потому что мы не знаем стандартное отклонение в генеральной совокупности.

Сравнение двух средних; t-критерий Стьюдента

Критерий, который позволяет сравнивать средние значения двух выборок между собой, называется t-критерий Стьюдента.

Условия для корректности использования t-критерия Стьюдента:

Две независимые группы

Формула стандартной ошибки среднего:

Формула числа степеней свободы:

Формула t-критерия Стьюдента:

Переход к p-критерию:

Проверка распределения на нормальность, QQ-Plot

Однофакторный дисперсионный анализ

Часто в исследованиях необходимо сравнить несколько групп между собой. В таком случае применятся однофакторный дисперсионный анализ.

Незвисимая переменная - номинативная перменная с нескольким градациями, разделяющая наблюдения на группы.

Зависимая перемнная - количественная переменная, по степени выраженности которой сравниваются группы.

Читайте также: