Плотность распределения двумерной случайной величины и ее свойства реферат

Обновлено: 09.07.2024

Функция распределения F (x, y) есть вероятность попадания в бесконечный квадрант D, который можно рассматривать как прямоугольник, ограниченный абсциссамиоо и х и ординатами — и у. Иглу длиной / бросают на плоскость, на которой на расстоянии L друг от друга проведены параллельные линии. Определите вероятность пересечения иглой одной из линий, если / Читать ещё >

теория вероятностей и математическая статистика

Плотность вероятности двумерной случайной величины ( реферат , курсовая , диплом , контрольная )

Двумерная случайная величина (X, Y) называется непрерывной, если ее функция распределения F (x, y)~ непрерывная функция, дифференцируемая по каждому из аргументов, и существует вторая смешанная производная F (х, у).

Как и для одномерной случайной величины, введем понятие плотности вероятности двумерной СВ.

Оценим вероятность попадания случайной точки в прямоугольник со сторонами Ах и, А у. Средняя плотность вероятности в данном прямоугольнике равна отношению вероятности к площади прямоугольника Ах-Л у. Будем неограниченно уменьшать стороны прямоугольника, устремив Ах и А у к нулю. С учетом (5.9) получим:

Учитывая то, что функция F (x, y) непрерывная и дифференцируемая по каждому аргументу, выражение (5.10) примет вид:

Плотностью вероятности (плотностью распределения, или совместной плотностью) непрерывной двумерной случайной величины (X, Y) называется вторая смешанная частная производная ее функции распределения:

Плотность распределения двумерной СВ обладает свойствами, аналогичными свойствам плотности вероятности одномерной СВ:

1. Плотность распределения двумерной случайной величины есть неотрицательная функция, то есть

Это свойство вытекает из того, что F (x, y) — функция неубывающая по каждому аргументу.

2. Вероятность попадания непрерывной двумерной случайной величины (Х, У) в область D равна

3. Функция распределения непрерывной двумерной случайной величины выражается через ее плотность вероятности по формуле:

Функция распределения F (x, y) есть вероятность попадания в бесконечный квадрант D, который можно рассматривать как прямоугольник, ограниченный абсциссамиоо и х и ординатами — и у.

4. Двойной несобственный интеграл в бесконечных пределах от плотности вероятности двумерной СВ равен единице:

Несобственный интеграл (5.16) есть вероятность попадания во всю плоскость Оху, а вероятность достоверного события равна 1 ["https://referat.bookap.info", 6].

Зная плотность вероятности двумерной СВ (X, Y), можно найти функции распределения и плотности вероятностей ее одномерных составляющих X и Y. Учитывая (5.6) и (5.15), получим:

Дифференцируя функции распределения F,(x) и F₂(y) по аргументам х и у соответственно, получим плотности вероятности одномерных СВ:

т. е. несобственный интеграл в бесконечных пределах от совместной плотности р (х, у) двумерной случайной величины по аргументу х дает плотность вероятности рг (у), а по аргументу у — плотность вероятности р,(х).

ПРИМЕР 1. Задано распределение вероятностей дискретной двумерной случайной величины:

Действительно, по определению плотность распределения есть предел отношения двух неотрицательных величин: вероятности попадания в прямоугольник и площади прямоугольника – и, следовательно, отрицательной быть не может.

2) Вероятность попадания случайной точки (X,Y) в область D равна двойному интегралу от плотности по области D:

Действительно, разбив область D на прямоугольники и применив к каждому из них равенство (13), получаем, по теореме сложения вероятностей, при стремлении к нулю площадей прямоугольников (то есть при и ), формулу (15). Геометрически эта вероятность изображается объёмом цилиндрического тела, ограниченного сверху поверхностью распределения и опирающегося на область D.

3) Функция распределения двумерной случайной величины выражается через плотность распределения следующим образом:

Эта формула следует из (13), так как F(x,y) есть вероятность попадания в прямоугольник, ограниченный абсциссами и ординатами .

4) Условие нормировки: двойной несобственный интеграл в бесконечных пределах от плотности вероятности двумерной случайной величины равен единице:

Действительно, этот интеграл есть вероятность попадания во всю плоскость xOy, то есть вероятность достоверного события. Геометрически свойство 4 означает, что объём тела, ограниченного поверхностью распределения и плоскостью xOy, равен единице.

5) Плотности распределения компонент двумерного случайного вектора могут быть получены по формулам:

Доказательство. Принимая во внимание, что

Продифференцировав обе части этого равенства по х, получим формулу (19):

Аналогично выводится формула (20).

Пример 5. Двумерная случайная величина (X,Y) задана плотностью распределения вероятностей .

Найти: 1) А; 2) ; 3) и .

Решение:1) Постоянную А найдём, используя условие нормировки:

2) Используя формулу (14), находим:

Можно было сначала по формуле (17) найти функцию распределения

и затем воспользоваться формулой (8):

Ответ:

Система n случайных величин

Перейдём теперь к системе n случайных величин или к n-мерной случайной величине.

Функция распределения n-мерной случайной величины - это вероятность совместного выполнения неравенств вида: i

Плотность вероятностей j(х, у) обладает свойствами, аналогичными свойствам плотности вероятности одномерной случайной величины:

1. Плотность вероятности двумерной случайной величины есть неотрицательная функция, т.е. j(x,y) ³ 0.

Свойство вытекает из определения плотности вероятности как предела отношения (см. 12, лекция 9) двух неотрицательных величин, ибо функция распределения Fx,y) – неубывающая функция по каждому аргументу.

2. Вероятность попадания непрерывной двумерной величины (X, Y) в область D равна

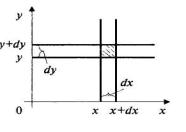
Эта вероятность приближенно равна объему элементарного параллелепипеда с высотой j(x, y), опирающегося на элементарный прямоугольник со сторонами dx и dy.

3. Если вероятность попадания одномерной случайной величины на отрезок [a, b] геометрически выражалась площадью фигуры, ограниченной сверху кривой распределения j(x) и опирающейся на отрезок [a, b], и аналитически выражалась интегралом , то вероятность попадания двумерной случайной величины в область D на плоскости Оху геометрически изображается объемом цилиндрического тела, ограниченного сверху поверхностью распределения j(x, y) и опирающегося на область D, а аналитически – двойным интегралом (1).

4. Функция распределения непрерывной двумерной случайной величины может быть выражена через ее плотность вероятности по формуле

Функция распределения F(x,y) есть вероятность попадания в бесконечный квадрант D, который можно рассматривать как прямоугольник, ограниченный абсциссами -¥ и х и ординатами -¥ и у. Поэтому в соответствии с (1)

5. Двойной несобственный интеграл в бесконечных пределах от плотности вероятности двумерной случайной величины равен единице.

Несобственный интеграл (3) есть вероятность попадания во всю плоскость Оху, т.е. вероятность достоверного события, равная 1. Это означает, что полный объем тела, ограниченного поверхностью распределения и плоскостью Оху, равен 1.

Зная плотность вероятности двумерной случайной величины (X, У), можно найти функции распределения и плотности вероятностей ее одномерных составляющих X и Y.

Так как в соответствии с (7) предыдущей лекции F(x,+¥) = F₁(x) и F(+¥,y) = F₂(y), то взяв в формулах (2) соответственно y = +¥ и x = +¥, получим функции распределения одномерных случайных величин X и Y

Дифференцируя функции распределения F₁(x) и F₂(y) соответственно по аргументам x и y, получим плотности вероятности одномерных случайных величин X и Y

т.е. несобственный интеграл в бесконечных пределах от совместной плотности j(x, y) двумерной случайной величины по аргументу x дает плотность вероятности j₂(y), а по аргументу у — плотность вероятности j₁(x).

Замечание.Если имеется кривая распределения j(x) одномерной случайной величины X, то конкретное значение ее плотности вероятности в данной точке х определяется геометрически ординатой кривой j(x). Если имеется поверхность распределения j(x, y) двумерной случайной величины (X, Y), то конкретное значение ее совместной плотности в данной точке (х, у) определяется геометрически аппликатой по поверхности j(x, y). В этом случае конкретное значение плотности вероятности j₁(x) одномерной составляющей X в данной точке х, в соответствии с (4), определится геометрически площадью сечения поверхности j(x, y) плоскостью X = х, параллельной координатной плоскости Oyz и отсекающей на оси Ох отрезок х. Аналогично конкретное значение плотности j₂(y) одномерной составляющей Y в данной точке y есть площадь сечения поверхности j(x, y) плоскостью Y = y, параллельной координатной плоскости Oxz и отсекающей на оси Оу отрезок у (см. рис. 2, на котором значение j₂(y) при данном y представляет площадь сечения, равную s).

Задача 1Двумерная случайная величина распределена равномерно в круге радиуса R = 1 (рис. 2). Определить: а) выражение совместной плотности и функции распределения двумерной случайной величины (X, Y); б) плотности вероятности и функции распределения одномерных составляющих X и Y; в) вероятность того, что расстояние от точки (X, Y)до начала координат будет меньше 1/3.

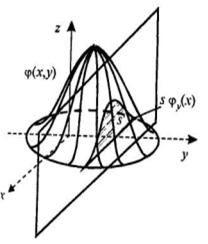
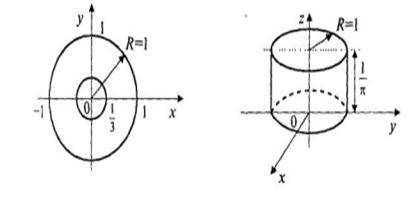
Рис. 2 Рис. 3 Рис. 4

Решение.

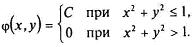
Постоянную С можно найти из соотношения (3)

Проще это сделать, исходя из геометрического смысла соотношения (3), означающего, что объем тела, ограниченного поверхностью распределения j(x,y) и плоскостью Охy, равен 1. В данном случае, это объем цилиндра с площадью основания pR 2 = p*1 2 = p и высотой С (рис. 4), равный p*C = 1, откуда C = 1/p. Следовательно

1/p, если х 2 +у 2 £ 1

0, если х 2 +у 2 > 1.

Найдем функцию распределения F(x, y) по формуле (2):

Очевидно, что этот интеграл с точностью до множителя 1/p совпадает с площадью области D – области пересечения круга х 2 + у 2 £ 1 с бесконечным квадрантом левее и ниже точки М(х, у)(рис. 5).

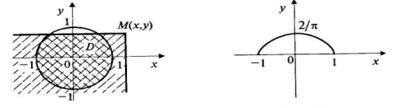
Для различных x и y можно по формуле (2) посчитать значения функции распределения двумерной случайной величины. Отметим очевидное, что при х £ –1, –¥ 1, у > 1, F(х, у) = 1, так как при этом область D полностью совпадает с кругом х 2 + у 2 £ 1, на котором совместная плотность (x,y) отлична от нуля;

б) Найдем функции распределения одномерных составляющих X и Y. По формуле (4) при –1 2 +Y 2

Друг друга берегите, дорожите! Ведь жизнь она у каждого одна. И в радости, и в горе поддержите, иначе - нам как людям "ГРОШ" цена! © Автор неизвестен ==> читать все изречения.

Функция распределения одной случайной величины не может описать все многообразие природных и, в том числе, экономических процессов и явлений. Для описания этих процессов используются двумерные и многомерные случайные величины. В данной главе остановимся на двумерных случайных величинах.

Двумерной случайной величиной называется функция вероятного события, наступившего в результате принятия величинами х и y случайных значений.

X и Y случайные величины, которые могут быть как дискретными, так и непрерывными.

Двумерную случайную величину можно интерпретировать как случайно взятую точку на плоскости Оxy, где x и y координаты этой точки.(Рис.1) Т.е. функция распределения F (x,y) есть вероятность попадания случайной точки в квадрант с вершиной в точке А(x,y), лежащей левее и ниже этой точки.

Для дискретной случайной величины функция распределения имеет следующий вид:

Свойства функции распределения двумерной случайной величины.

1.Функция 0 ≤ F(x,y) ≤ 1, т.е. величина неотрицательная меньше 1.

2.Функция F(x,y) есть возрастающая функция по каждому из аргументов.

3.Функция распределения F(x,y) = 0, если хотя бы один из аргументов x или y стремится к минус бесконечности.

4.Функция F(x,y) равна функции от одного аргумента F(x) (F(y)), если y (x) стремится к бесконечности.

5. Функция F(x,y) равна 1, если оба аргумента стремятся к плюс бесконечности.

Геометрический смысл функции распределения есть поверхность на координатной плоскости Оxy.(Рис.2) Значение функции равно вероятности попадания случайной величины в область, рассчитанную по формуле:

Формула рассчета вероятности, состоящая из 4-х слагаемых, объясняется тем, что вероятность равна вероятности попадания случайной величины в бесконечный квадрант, исходящий из точки В, минус квадрант в точках А и С и плюс бесконечный квадрант в точке D, т.к. квадрант в точке D был вычтен дважды.

Репетитор: Васильев Алексей Александрович

Предметы: математика, физика, информатика, экономика, программирование.

2000 руб / 120 мин - подготовка к ЕГЭ и ГИА для школьников. 3000 руб / 120 мин - индивидуально (базовый уровень). 2000 руб / 120 мин - студенты.

2.Плотность вероятности двумерной случайной величины.

Как известно, случайная величина имеет плотность вероятности, если она непрерывна. Говоря о случайных величинах, двумерная случайная величина называется непрерывной, если ее функция распределения является непрерывной функцией. И существует вторая смешанная производная F '' xy (x,y), которая и является плотностью вероятности двумерной случайной величины.

Т.е. плотность вероятности это вторая смешанная производная от функции распределения двумерной случайной величины:

В общем виде плотность вероятности двумерной случайной величины выражается следующей формулой:

r - коэффициент корреляции случайных величин X и Y
σ x - среднее квадратическое отклонение случайной величины X
σ y - среднее квадратическое отклонение случайной величины Y
m x - математическое ожидание случайной величины X
m y - математическое ожидание случайной величины Y

Если случайные величины подчинены нормальному закону распределения и не коррелированы (r = 0 ), то формула плотности вероятности примет вид:

Геометрический смысл вероятности двумерной случайной величины - это поверхность похожая на купол. На рис.3 изображен график плотности вероятности с параметрами r, σ x , σ y , m x , m y , которые имеют следующие значения:

r = 0
σ x = 2
σ y = 2
m x = -1
m y = 1

Рассматривая выражения для плотности вероятности двумерной случайной величины, можно заметить, что данный закон распределения задается пятью параметрами: двух координат центра распределения случайных величин x и y по осям X и Y, средних квадратических отклонений σ x и σ y , и коэффициентом корреляции случайных величин x и y.

Вероятность попадания непрерывной двумерной случайной величины в область D равна:

Функция распределения непрерывной двумерной случайной величины имеет вид:

Пример 1

Двумерная случайная величина распределена равномерно в геометрической фигуре ограниченной осью Ox и параболой y = x² - 1 (рис.4). Найти выражение совместной плотности и функции распределения двумерной случайной величины (X,Y). Найти также плотности вероятности и функции распределения одномерных составляющих X и Y и вероятность того, что расстояние от точки (X,Y) до оси X будет не больше 3/4.

Читайте также: