Основные законы алгебры логики реферат

Обновлено: 02.07.2024

Алгебра логики это математический аппарат, позволяющий выполнять операции с логическими высказываниями. Другое название – алгебра высказываний.

С помощью этого понятия производятся вычисления, упрощения и преобразования с исходными суждениями.

Логическое высказывание или суждение – это предложение с истинным или ложным значением.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Сегодня идет дождь.

Основные законы алгебры логики

Законы алгебры высказываний представляют собой тавтологии и также называются теоремами. Запись законов раздела математической логики осуществляется в виде эквивалентных формул.

Закон тождества

Теорема представлена в виде формулы: A=A.

Рассматриваемый закон гласит, что любое высказывание тождественно самому себе. При рассуждении недопустима подмена одной мысли или понятия другими. В противном случае может возникнуть логическая ошибка.

Закон непротиворечия

Записывается в виде: \(A\&Ā=0\)

Рассматриваемая теорема означает, что суждение в конкретный момент времени может иметь или истинное, или ложное значение, третье исключено.

Бизнес несет убытки или не несет.

Это высказывание – ложь. Его истинность исключается, так как в предложении утверждается, что оно ложно. В то же время рассматриваемое высказывание не может быть ложью, иначе оно являлось бы истинным. Данное предложение не ложь, и не истина, поэтому закон исключенного третьего нарушается.

В данном случае противоречие объясняется ссылкой суждения на самого себя. Возникающий в этом примере парадокс является доказательством того, что рассматриваемый закон не всегда применим.

Закон двойного отрицания

Записывается в виде \(\overset=A=A\)

Означает, что при двойном отрицании исходного суждения в итоге получится оно же.

Шторы – элемент декора окон. Неверно, что шторы не являются элементом декора окон.

Свойства констант

Отрицание лжи есть истина:

Отрицание истины есть ложь:

Закон идемпотентности

Теорема идемпотентности – это закон, дающий возможность исключить повторяющиеся суждения.

В записи данный закон выглядит так:

От того, сколько раз мы скажем – свет включен или свет включен или свет включен – значение предложения не поменяется.

Закон коммутативности

На следующей неделе будет ясно или пасмурно только при условии, что на следующей неделе будет ясная погода или пасмурная погода.

Закон ассоциативности

Теорема утверждает, что логическое сложение и умножение ассоциативно, то есть при наличии в выражении лишь конъюнкции или лишь дизъюнкции можно опускать скобки:

\(A\cup(B\cup C)=(A\cup B)\cup C\)

Законы дистрибутивности

Рассматриваемая теорема является правилом раскрытия скобок при конъюнкции и дизъюнкции.

Дистрибутивность логического сложения относительно логического умножения имеет значение – А или (В и С) есть тоже самое, что А или В и А или С – и записывается формулой:

Дистрибутивность логического умножения над логическим сложением читается как – А и (В или С) есть тоже самое, что А и В или А и С – и имеет вид:

Закон поглощения

Теорема, при которой верны следующие равенства:

Законы де Моргана

\(\overline=\overline A\cup\overline B\)

Закон де Моргана для дизъюнкции означает, неверно, что А и В, если и только если неверно А и неверно В. Данное выражение можно записать в виде формулы:

\(\overline=\overline A\&\overline B\)

Формы представления функций алгебры логики

Существует три способа представления выражений:

в виде таблицы истинности;
аналитическая форма;
логическая форма.

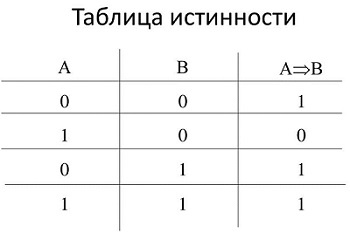
Таблица истинности

При этом способе комбинации логических переменных они расположены в порядке возрастания их двоичного номера. Наборы переменных обозначаются числами от нуля до 2n − 1, где n – количество переменных функции. При наличии значений на всех комбинациях функция называется полностью определенной.

Аналитическое выражение

Рассмотрение данной формы невозможно без введения новых понятий.

терм – компонент выражения;
ранг терма – число переменных в терме;
дизъюнктивный терм (макстерм) – логическое сложение произвольного количества попарно независимых переменных;
конъюнктивный терм (минтерм) – логическое умножение произвольного количества попарно независимых переменных.

В аналитической записи используют две формы выражения:

\(f(a,b,c)=\overline ab\overline c+a\overline b+a\overline c+b\)

При условии, что все термы, составляющие нормальную форму, имеют одинаковый и максимальный ранг, который равен количеству переменных функции, форма называется совершенной. В такой форме минтерм – конституентная единицы, макстерм – конституентная нуля.

Совершенная дизъюнктивная форма (дизъюнкция конституент единицы) записывается так:

\(F(a,b,c)=\overline abc+abc+abc+ab\overline c\)

Совершенная конъюнктивная форма (конъюнкция конституент нуля) имеет вид:

\(F(a,b,c,d)=(a+b+\overline c+d)(\overline a+b+\overline c+d)(\overline a+\overline d+\overline c+d)\)

Аналитические формы полностью дуальны.

Числовая запись

Данный вид записи функций алгебры логики позволяет представить ее компактно.

Вид для совершенной дизъюнктивной нормальной формы:

Вид для совершенной конъюнктивной нормальной формы:

Логические операции

Сложные логические суждения формируются из простых логических операций. Основные логические операции:

конъюнкция или логическое умножение;
дизъюнкция или логическое сложение;
инверсия или логическое отрицание.

Конъюнкция

В основе логического умножения стоят два высказывания, в соответствие с которыми ставится новое суждение, являющееся истиной лишь в том случае, когда оба исходных высказывания истинны.

Конъюнкция может быть записана следующими способами:

Дизъюнкция

При логическом сложении двух исходных суждений получается новое высказывание, ложное лишь в том случае, когда оба исходных суждения ложны.

Графическое обозначение дизъюнкции:

Инверсия

При логическом отрицании в соответствие каждому суждению ставится противоположное исходному высказывание.

Разложение в дизъюнкцию

Составление совершенных форм происходит по таблице истинности функции.

Правило для составления дизъюнкции конституент единицы: для каждой комбинации переменных, где функция истинна, записывается минтерм ранга n>, где переменные с нулевым значением в рассматриваемом наборе берутся с отрицанием. Все конъюнктивные термы объединяют дизъюнктивно. СДНФ для номеров N=1, 3, 6, 7:

\(f(a,b,c)=\overline a\overline bc+\overline abc+ab\overline c+abc\)

Разложение в конъюнкцию

Правило составления конъюнкции конституент нуля по таблице истинности: для каждого набора переменных, где функция имеет ложное значение, записывают дизъюнктивный терм ранга n, в котором переменные с единичными значениями на данной комбинации берутся с отрицанием. Все макстермы объединяют конъюнктивно. СКНФ для номеров наборов N=0, 2, 4, 5:

\(f(a,b,c)=(a+b+c)(a+\overline b+c)(\overline a+b+c)(\overline a+b+\overline c)\)

Как составить таблицу истинности

Алгоритм построения таблицы истинности:

Определить число переменных функции.
Посчитать, сколько всего операций в выражении.
Учесть скобки и установить порядок выполнения логических операций.
Узнать количество столбцов в таблице путем сложения количества переменных и числа операций.
В шапке таблицы записать переменные и операции в установленном в п.3 порядке.
Определить количество строк в таблице (без шапки) по формуле m=2n.
Выписать комбинации входных переменных, представленных в виде целого ряда двоичных чисел от 0 до 2n−1 с разрядом n.
Заполнить столбцы таблицы, последовательно совершая логические операции.

В выражении A&B две переменные и одна операции – конъюнкция. Количество столбцов для данного примера – 3:

Алгебра высказываний (алгебра логики) — раздел математической логики, изучающий логические операции над высказываниями и правила преобразования сложных высказываний.

При решении многих логических задач часто приходится упрощать формулы, полученные при формализации их условий. Упрощение формул в алгебре высказываний производится на основе эквивалентных преобразований, опирающихся на основные логические законы.

Законы алгебры высказываний (алгебры логики) — это тавтологии.

Иногда эти законы называются теоремами.

В алгебре высказываний логические законы выражаются в виде равенства эквивалентных формул. Среди законов особо выделяются такие, которые содержат одну переменную.

Первые четыре из приведенных ниже законов являются основными законами алгебры высказываний.

Закон тождества:

Всякое понятие и суждение тождественно самому себе.

Закон тождества означает, что в процессе рассуждения нельзя подменять одну мысль другой, одно понятие другим. При нарушении этого закона возможны логические ошибки.

Закон непротиворечия :

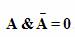
В один и тот же момент времени высказывание может быть либо истинным, либо ложным, третьего не дано. Истинно либо А, либо не А. Примеры выполнения закона исключенного третьего:

1. Число 12345 либо четное, либо нечетное, третьего не дано.

2. Предприятие работает убыточно или безубыточно.

3. Эта жидкость является или не является кислотой.

Рассмотрим следующее высказывание: Это предложение ложно. Оно не может быть истинным, потому что в нем утверждается, что оно ложно. Но оно не может быть и ложным, потому что тогда оно было бы истинным. Это высказывание не истинно и не ложно, а потому нарушается закон исключенного третьего.

Парадокс (греч. paradoxos — неожиданный, странный) в этом примере возникает из-за того, что предложение ссылается само на себя. Другим известным парадоксом является задача о парикмахере: В одном городе парикмахер стрижет волосы всем жителям, кроме тех, кто стрижет себя сам. Кто стрижет волосы парикмахеру? В логике из-за ее формальности нет возможности получить форму такого ссылающегося самого на себя высказывания. Это еще раз подтверждает мысль о том, что с помощью алгебры логики нельзя выразить все возможные мысли и доводы. Покажем, как на основании определения эквивалентности высказываний могут быть получены остальные законы алгебры высказываний.

Например, определим, чему эквивалентно (равносильно) А (двойное отрицание А , т. е. отрицание отрицания А ).Для этого построим таблицу истинности:

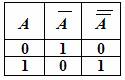
По определению равносильности мы должны найти тот столбец, значения которого совпадают со значениями столбца А. Таким будет столбец А.

Таким образом, мы можем сформулировать закон двойного отрицания:

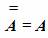
Если отрицать дважды некоторое высказывание, то в результате получается исходное высказывание. Например, высказывание А = Матроскин — кот эквивалентно высказыванию А = Неверно, что Матроскин не кот .

Аналогичным образом можно вывести и проверить следующие законы:

Свойства констант:

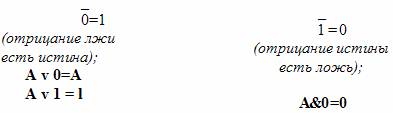
Законы идемпотентности:

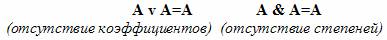
Сколько бы раз мы ни повторяли: телевизор включен или телевизор включен или телевизор включен . значение высказывания не изменится. Аналогично от повторения на улице тепло, на улице тепло. ни на один градус теплее не станет.

Законы коммутативности:

Операнды А и В в операциях дизъюнкции и конъюнкции можно менять местами.

Законы ассоциативности:

A v(B v C) = (A v B) v C;

А & (В & C) = (A & В) & С.

Если в выражении используется только операция дизъюнкции или только операция конъюнкции, то можно пренебрегать скобками или произвольно их расставлять.

Законы дистрибутивности:

A v (B & C) = (A v B) &(A v C)

(дистрибутивность дизъюнкции
относительно конъюнкции)

А & (B v C) = (A & B) v (А & C)

(дистрибутивность конъюнкции
относительно дизъюнкции)

Закон дистрибутивности конъюнкции относительно дизъюнкции аналогичен дистрибутивному закону в алгебре, а закон дистрибутивности дизъюнкции относительно конъюнкции аналога не имеет, он справедлив только в логике. Поэтому необходимо его доказать. Доказательство удобнее всего провести с помощью таблицы истинности:

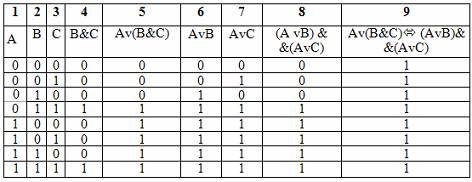
Законы поглощения:

Проведите доказательство законов поглощения самостоятельно.

Законы де Моргана:

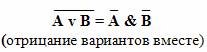
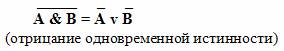
Словесные формулировки законов де Моргана:

Мнемоническое правило: в левой части тождества операция отрицания стоит над всем высказыванием. В правой части она как бы разрывается и отрицание стоит над каждым из простых высказываний, но одновременно меняется операция: дизъюнкция на конъюнкцию и наоборот.

Примеры выполнения закона де Моргана:

1) Высказывание Неверно, что я знаю арабский или китайский язык тождественно высказыванию Я не знаю арабского языка и не знаю китайского языка.

2) Высказывание Неверно, что я выучил урок и получил по нему двойку тождественно высказыванию Или я не выучил урок, или я не получил по нему двойку.

Замена операций импликации и эквивалентности

Операций импликации и эквивалентности иногда нет среди логических операций конкретного компьютера или транслятора с языка программирования. Однако для решения многих задач эти операции необходимы. Существуют правила замены данных операций на последовательности операций отрицания, дизъюнкции и конъюнкции.

Так, заменить операцию импликации можно в соответствии со следующим правилом:

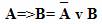
Для замены операции эквивалентности существует два правила:

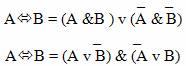
В справедливости данных формул легко убедиться, построив таблицы истинности для правой и левой частей обоих тождеств.

Знание правил замены операций импликации и эквивалентности помогает, например, правильно построить отрицание импликации.

Информатика не может существовать без такого важного раздела математики, который называется алгеброй логики. В данной статье будет рассказана основополагающая информация по данной теме, обозначены её главные правила и законы.

Что такое алгебра и алгебра логики

Алгебра — это раздел математики, который обобщенно можно охарактеризовать, как расширение и обобщение арифметики.

Алгебра логики — это раздел математической логики, который исследует операции над высказываниями.

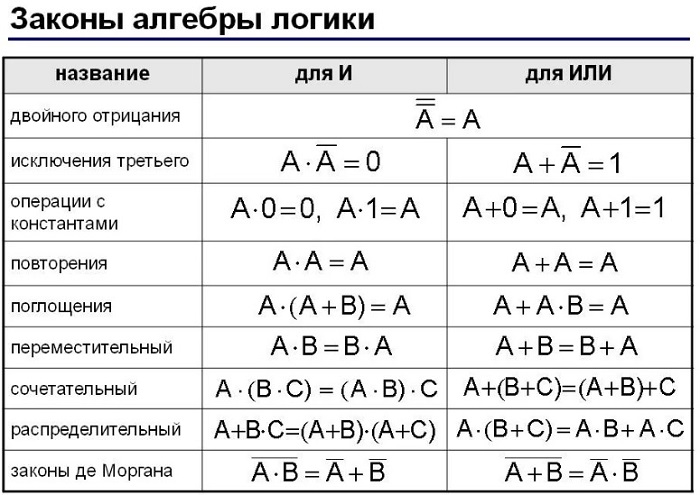
Законы алгебры логики

Имеется большое количество правил в данной сфере деятельности, но сегодня будет рассмотрено несколько основных.

Переместительный закон - предназначен для процесса сложения и вычитания. Суть данного правила в том, что обозначения А и В в операциях дизъюнкции и конъюнкции можно менять.

Сочетательный закон - применяется, когда есть или только операция дизъюнкции, или только операция конъюнкции. Тогда можно обходиться без скобок или хаотично ставить скобки.

Распределительный закон - имеется два типа данного правила: дистрибутивность дизъюнкции относительно конъюнкции и дистрибутивность конъюнкции относительно дизъюнкции. Первый тип схож с дистрибутивным законом алгебры, а второй — нет, поэтому его нужно доказывать.

Закон двойственности и инверсии (закон Моргана) - основоположником данного правила стал шотландский математик и логик де Морган. Он разработал правило, которое связывает логические операции конъюкцию (И) и дизъюнкцию (ИЛИ) с помощью отрицания.

Основные законы алгебры логики представлены в таблице:

Логические выражения

В информатике предоставляется два вида высказываний: простое и сложное.

Простое — это утверждение, которое обычно обозначается в виде предложения и про него можно сказать — ложное оно или истинное.

Нью-Йорк — столица США (ложное);

в России 1117 городов (верное).

Сложное высказывание обозначает некий набор простых утверждений, которые связаны логическими процессами.

Идёт дождь, а у меня нет зонта.

Основные логические операции

Логические процессы подразделяются на несколько классов. Рассмотрим их последовательно.

Логическое отрицание (инверсия) —НЕ

Данная операция используется при обозначении отрицания. Она обозначается знаками — NO, NOT, ! В=2 (истина), а после выполнения операции отрицания, В, к примеру, приобретет значение 1 (ложное).

Таблица истинности инверсии:

Результаты операции НЕ следующие:

если исходное выражение истинно, то результат его отрицания будет ложным;

если исходное выражение ложно, то результат его отрицания будет истинным.

Логическое сложение (дизъюнкция, объединение) — ИЛИ

Таблица истинности операции ИЛИ:

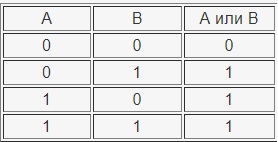
Логическое умножение(конъюнкция) — И

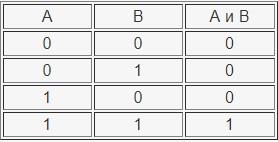
В истории данная операция также обозначается как логическое умножение и конъюнкция. Данная операция обозначается элементами — И, AND, &&, &.

За объект описания возьмём А и В. Оба данных выражения могут иметь или неверное значение, или правдивое значение. Для применения операции логическое умножение, и А, и В должны является истинными (то есть равными единице).

При всех остальных значениях операция будет ложной.

Таблица истинности операции И приведена ниже:

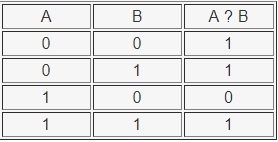
Логическое следование (импликация) — ЕСЛИ ТО

Необходимо запомнить, что данная операция ложна только тогда, когда из первого ложного утверждения следует ложный итог. На компьютерном языке данный процесс обозначается формулой: if. then.

Таблица истинности операции ЕСЛИ ТО выглядит так:

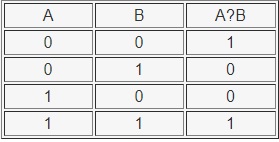
Операция эквивалентности (равнозначности) - А ТОГДА И ТОЛЬКО ТОГДА, КОГДА В

Данная операция определяется так: сложное высказывание будет истинно тогда и только тогда, когда и А, и В — истинные.

И наоборот: сложное высказывание будет ложным тогда и только тогда, когда и А, и В — ложные.

Таблица истинности операции эквивалентности:

В современном мире одной из наиболее интересных и древних наук,
безусловно, является логика. Логика, как наука стала формироваться еще в
древней Греции примерно две с половиной тысячи лет назад.
Данная наука в процессе развития человеческой цивилизации
претерпевала значительная изменения и на сегодняшний день её методы, и
принципы позволяют принимать наиболее эффективные и рациональные
решения. Основой логики являются её законы, которые определяют
основные принципы интеллектуальной познавательной деятельности
человека в различных сферах. К основным законам логики относятся
следующее:
- закон тождества;
- закон противоречия;
- закон исключения третьего;
- закон достаточного основания.
Логической законы являются фундаментом данной науки и
представляют собой большой интерес так, как от их эффективного
использования зависит эффективность принимаемых решений, именно этим
и объясняется актуальность выбранной темы исследования.
Целью данной работы является рассмотрение основных законов логики
принятых на сегодняшний день.

1. Основные законы логики. Закон тождества

2. Закон противоречия

делает воинствующее заявление насчет того, что убеждений никаких нет и не
может быть, причем отстаивает данный персонаж свое пессимистическое
мнение горячо и убежденно.
- Так вы говорите: никаких убеждений нет? — спрашивает Рудин.
- Нет и быть не может.
- Это ваше убеждение?
- Да.
- Как же вы утверждаете, что их нет? Вот вам одно на первый случай.
Утверждая что-либо о каком-либо объекте, мы не можем, не
противореча себе, отрицать то же самое о том же самом объекте, взятом в то
же самое время и в том же самом отношении. Второй закон обеспечивает
непротиворечивость и последовательность мышления, способность
фиксировать и исправлять всякого рода противоречия в своих и чужих
рассуждениях.

3. Закон исключенного третьего

Посредством использования данного закона достигается однозначность
логического мышления.

4. Закон достаточного основания

Сущность закона достаточного основания представляет собой то, что
любая мысль является истиной только в том случае, когда мысль имеет
достаточное основание, таким образом, любая мысль должна иметь
аргументы подтверждающие её, быть обоснованной. Всякая мысль является
истинной или ложной не сама по себе, а в силу достаточного основания. Это
значит: любое положение, прежде чем стать научной истиной, должно быть
подтверждено различными аргументами, достаточными для признания его
твердо и неопровержимо доказанным.
Достаточным основанием какой-либо мысли может быть любая другая,
уже проверенная и признанная истинной мысль, из которой вытекает
истинность рассматриваемой мысли. Закон позволяет обеспечить
обоснованность мыслительного процесса. Во всех случаях, когда мы
утверждаем что-либо, мы обязаны доказать свою правоту, то есть, привести
достаточные основания, подтверждающие истинность наших мыслей.
Заключение

Таким образом, на современном этапе развития науки логики
сформировались определенные законы, способствующие решению
различных задач наиболее эффективным, рациональным образом.
Следование принципам и методам применяемых в данных законах,
безусловно, является важнейшей предпосылкой правильно мышления.
Использование законов логики позволяет достигнуть истины в той или
иной степени, а также снижает шанс получения неверного суждения в
процессе поиска истинного знания об определенном предмете или явлении.
В этой связи, абсолютно любому человеку необходимо
руководствоваться основными законами логики так, как именно они
позволяют достигнуть истины, избегая, различные заблуждения,
встречающиеся на пути поиска истины.

Список использованной литературы

1. А.Д. Гетманова. Логика. – М.: КноРус, 2012. – 240 с.
2. А.К. Сковиков. Логика. – М.: Юрайт, 2013. – 576 с.
3. В.И. Кириллов, А.А. Старченко. Логика. Учебник. – М.: Проспект, 2016. –
240 с.
4. Д.А. Гусев. Логика. Учебное пособие. – М.: Прометей, 2015. – 300 с.
6. Елена Зарецкая. Логика. Практическое пособие. – М.: LAP Lambert
Academic Publishing, 2014. – 152 с.
7. С.К. Абачиев. Формальная логика с элементами теории познания. –
Ростов-на-Дону: Феникс, 2011. – 640 с.

Читайте также: