Определение положения точек на земной поверхности реферат
Обновлено: 26.07.2024
Координатные данные, составляющие один из основных классов геоинформационных данных, используют для указания местоположения на земной поверхности.
Поверхность Земли имеет сложную форму. При общей площади ее поверхности 510 млн. км 2 71 % приходится на дно морей и океанов и 29 % - на сушу. Это дает основание считать, что земная поверхность состоит из двух резко отличающихся морфологических элементов - материков и океанов.
С учетом того, что поверхность вод Мирового океана занимает почти 3/4 поверхности Земли, за общую фигуру земли принимают тело, ограниченное поверхностью воды океанов. Такая поверхность называетсяуровненной. Потенциал силы тяжести на ней имеет одно и то же значение. Другими словами, эта поверхность везде перпендикулярна отвесной линии, т.е. везде горизонтальна.
Можно построить семейство горизонтальных поверхностей. Поверхность, которая совпадает с поверхностью Мирового океана в состоянии покоя и равновесия и продолжена под материками, образует фигуру, принятую в геодезии за общую фигуру Земли, называемуюгеоид.
С помощью методов дистанционного зондирования удалось установить, что Земля имеет грушевидную форму. В качестве математической модели Земли применяют эллипсоид, который в геодезии принято называтьреференц-эллипсоидом. В СССР до 1946 г. использовался эллипсоид, полученный Ф. Бесселем. В 1946 г. для обязательного использования был введен эллипсоид, вычисленный в ЦНИИГАиК в 1940 г. под руководством Ф.Н. Красовского при участии А.А. Изотова.
Для отображения положения точек поверхности на плоскости используют различные математические модели поверхности и различные системы координат. На практике применяют два основных типа координат: плоские и сферические. Реже применяют криволинейные или полярные.
Выбор системы координат зависит от размеров исследуемых участков поверхности, как следствие, от влияния кривизны Земли. При изображении небольших участков Земли часть уровненной поверхности можно принять за плоскость. Такими участками будут участки до 20 км длиной и площадью до 400 км 2 .
В этих случаях применимы плоские координаты.
Плоские декартовы координаты определяются заданием двух осей. При этом обычно координата Х указывает на восток, Y - на север. Задают масштабные отрезки. Упорядоченная пара (X, Y) определит положение точки в заданной системе.
Плоские полярные координаты используют расстояние от начала координат и угол от фиксированного направления. Направление обычно фиксируется на север, а угол отсчитывается по часовой стрелке от него. Полярные координаты удобны при проведении измерений от какой-либо заданной точки, например, когда используются данные таких источников, как радарные съемки.
При необходимости учета кривизны Земли применяют пространственные системы координат.
Для определения географической системы координат (разновидности сферической системы) введем следующие понятия:
• плоскость земного экватора - проходит через центр Земли перпендикулярно к оси вращения;
• плоскость географического (астрономического) меридиана - проходит через ось вращения Земли и отвесную линию в точке земной поверхности;
• меридиан - линия пересечения плоскостей географических меридианов с земной поверхностью;
• параллель - линия, образованная пересечением плоскости, параллельной плоскости земного экватора, с поверхностью Земли.
Положение точки определяется широтой и долготой.
Широта - это угол между точкой и экватором вдоль меридиана (Такое определение широты не годится для эллипсоида.). Она изменяется от -90 ° (южный полюс) до +90 ° (северный полюс).
Долгота - это угол в плоскости экватора между меридианом точки и главным (нулевым) меридианом, проходящим через Гринвич (Англия). Она изменяется от -180 ° (западная долгота) до +180 ° (восточная долгота).
Основными понятиями этой системы координат являются:
меридиан - линия постоянной долготы;
параллель - линия постоянной широты;
большой круг - воображаемый круг на земной поверхности, образованный плоскостью, проходящей через центр земного шара;
малый круг - воображаемый круг на земной поверхности, образованный плоскостью, не проходящей через центр земного шара.
Рассмотренные системы координат носят в большей степени теоретический характер. На практике используют более широкий набор систем координат: геоцентрические, топоцентрические, полярные геодезические, эллиптические и др.
Координатные данные
Геометрически информация, содержащаяся на карте, может быть определена как совокупность наборов точек, линий, контуров и площадей, имеющих метрические значения, отражающие трехмерную реальность. Эта информация образует класс координатных данных ГИС, являющийся обязательной характеристикой геообъектов. Будучи частью (классом) общей модели данных в ГИС, координатные данные определяюткласс координатных моделей.
Основные типы координатных моделей
Класс координатных моделей можно разбить на типы. При этом следует учесть, что попытка включить в описание широкий набор групп, приводит к усложнению базы данных и процессов обработки. В ГИС используют меньшее число атомарных моделей по сравнению с САПР. В ГИС, как и в САПР, применяют набор базовых геометрических типов моделей, из которых создают все остальные, более сложные. С учетом предметной области карт ограничиваются лишь описанием таких типов (структур географических данных), которые относятся к представлению топографии и к тематическому упорядочению.
В ГИС включают следующие основные типы координатных данных - (рис. 5.3.):
• точка (узлы, вершины);
• контур (замкнутая линия);
• полигон (ареал, район) - группы примыкающих друг к другу замкнутых участков.
В некоторых системах в описание основных типов моделей включают понятие пространственная сеть, которая является развитием типа данных район. Контуры и линии часто объединяют общим термином - "линейные объекты". Таким образом, в разных ГИС число основных типов координатных моделей меняется от трех до пяти. Проводя сравнение с технологиями САПР, отметим, что основные типы координатных данных являются аналогами атомарных моделей в САПР, которые называютпримитивами.
Приведенные выше понятия носят концептуальный характер. На практике для построения реальных объектов используют большее число составных координатных моделей. В разных ГИС они незначительно отличаются, поэтому рассмотрим в качестве примера набор данных в системе GeoDraw:
• точка - пара координатX, Y;
• отрезок - линия, соединяющая две точки;
• вершина (вертекс) - начальная или конечная точка отрезка;
• дуга (линия) - упорядоченный набор связных отрезков (или вершин);
Рис. 5.3. Основные типы координатных данных
• узел - начальная или конечная вершина дуги;
• висячий узел - узел, принадлежащий только одной дуге, у которой начальная и конечная вершины не совпадают;
• псевдоузел - узел, принадлежащий только двум дугам либо одной замкнутой дуге, у которой начальная и конечная вершины совпадают. Исключением является узел, принадлежащий двум дугам, одна из которых самозамкнута в этом узле, а другая примыкает к ней (такой узел является нормальным);
• нормальный узел - узел, принадлежащий трем (и более) дугам. Нормальным также является узел, принадлежащий двум дугам, одна из которых самозамкнута в этом узле, а другая примыкает к ней;
• висячая дуга - дуга, имеющая висячий узел;
• замкнутая дуга - дуга, у которой совпадают начальная и конечная вершины (у такой дуги имеется только один узел);
• полигон - единичная область, ограниченная (находящаяся внутри) замкнутой дугой или упорядоченным набором связных дуг, которые образуют замкнутый контур;
• покрытие - набор файлов, фиксирующий в виде цифровых записей пространственные объекты (точки, дуги, полигоны) и структуру отношений между ними;
• пустое покрытие - покрытие, в котором отсутствуют пространственные объекты;
• слой - покрытие, рассматриваемое в контексте его содержательной определенности (растительность, рельеф, административное деление и т.п.) или его статуса в среде редактора (активный слой, пассивный слой);
• внутренний идентификатор пространственного объекта - целое чисто, являющееся служебным идентификатором системы (уникальное для каждого объекта данного покрытия и назначаемое автоматически в процессе работы редактора). Может изменяться системой в процессе работы;
• пользовательский идентификатор (внутренний ключ) пространственного объекта - целое число, служащее для связи объектов цифровой карты с базой (таблицами) тематических данных. Назначается и изменяется только пользователем.
На рис. 5.4 показаны основные из рассмотренных элементы векторных данных ГИС.
Рис. 5.4. Основные элементы векторных данных ГИС
Точечные объекты. Простейший тип пространственного объекта задают точечные данные, к которым относятся не только точки, но и все точечные условные знаки. Выбор объектов, представляемых в виде точек, зависит от масштаба карты или исследования. Например, на крупномасштабной карте точками показываются отдельные строения, а на мелкомасштабной карте - города.
Особенность точечных объектов состоит в том, что они хранятся и в виде графических файлов, как другие пространственные объекты, и в виде таблиц, как атрибуты. Последнее обусловлено тем, что координаты каждой точки описывают как два дополнительных атрибута.
В силу этого информацию о наборе точек можно представить в виде развернутой таблицы или таблицы, содержащей помимо координат наборы атрибутов (идентификационные номера, тематические характеристики и т.д.). В таких таблицах каждая строка соответствует точке - в ней собрана вся информация о данной точке. Каждый столбец - это признак, содержащий типизированные данные: координаты или атрибуты. Каждая точка независима от всех остальных точек, представленных отдельными строками.
Линейные объекты. Они широко применяются для описания сетей, для которых в отличие от точечных объектов характерно присутствие топологических признаков.
Любая сеть состоит из узлов (вершин) - соединений, концов обособленных линий и звеньев (дуг) - цепей в модели базы данных.
Линейные объекты, как и точечные, имеют свои атрибуты, причем разные для дуг (звеньев) и узлов.
Атрибутами для дуг являются:
• направление движения, интенсивность движения, протяженность;
• количество полос, время пути вдоль звена;
• диаметр трубы, направление движения газа;
• напряжение в ЛЭП, высота опор;
• количество путей, уклон, ширина тоннеля, грузоподъемность и др.
Атрибуты для узла:
• наличие перехода, названия пересекающихся улиц;
• наличие автоматического регулирования перекрестков;
• тип (ручной или автоматический) перевода стрелок;
• характеристики трансформаторов ЛЭП;
Некоторые атрибуты (например, названия пересекающихся улиц) служат для связи одного типа объектов с другими (узлы со звеньями), другие характеризуют только участки звеньев сети.
Сети часто используют как системы линейной адресации. В этих случаях точки размещают в сети по данным о номере звена и о расстоянии от его начала. Это более удобно, чем использовать X, Y координаты точки из таблицы, поскольку такие данные непосредственно указывают положение точки в сети.
Данный подход определяет метод присвоения атрибутов отдельным участкам звеньев. При этом линейные объекты (здания, тоннели) хранятся в отдельных таблицах, а с сетью они увязаны путем указания номера звена и расстояния от его начала.
Для точечных объектов необходимо указать одно значение координат, для линейных - два (для начальной и конечной точек). Это позволяет при необходимости рассчитать X, Y координаты этих объектов и исключает необходимость дробить звенья и вводить двухвалентные узлы.
Ареалы. В настоящее время в ГИС может быть представлено несколько типов ареалов: зоны в приложении к окружающей среде или природным ресурсам, социально-экономические зоны, данные об угодьях и др.
Для ареальных объектов границы могут определяться свойством или явлением, а также независимо от явления (затем перечисляются значения атрибутов). Кроме того, границы могут устанавливаться искусственно, например для микрорайонов.
© 2014-2022 — Студопедия.Нет — Информационный студенческий ресурс. Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав (0.011)
- Для учеников 1-11 классов и дошкольников
- Бесплатные сертификаты учителям и участникам
Лекция 2. ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЯ ТОЧЕК НА ЗЕМНОЙ
ПОВЕРХНОСТИ
1. Географические координаты
2. Плоские прямоугольные координаты
3. Полярные и биполярные координаты
4. Система плоских прямоугольных координат Гаусса-Крюгера
1. Географические координаты
Широта — угол между плоскостью экватора и отвесной линией в данной точке. Широту параллели обозначают на рамках географических карт, а на глобусе — у пересечений параллелей с меридианами 0° и 180°. Широты изменяются от 0 до 90°. В северном полушарии они называются северными, а в южном — южными.
Долгота — угол, составленный плоскостью начального меридиана и плоскостью меридиана данной точки. Долготы, отсчитываемые на восток от Гринвичского меридиана, называются восточными, а долготы, отсчитываемые на запад, — западными. Долгота может иметь значения от 0° до 180°. На картах и глобусах долготы чаще всего обозначают у пересечения меридианов с экватором.
Чтобы определить широту какого-либо объекта, надо найти параллель, на которой он находится. Например, столица Египта Каир расположен на параллели 30° и лежит к северу от экватора, следовательно, широта Каира северная и составляет 30° северной широты (с.ш.). А если объект находится не на тех параллелях, что подписаны на карте, а между ними? Тогда надо определить широту ближайшей к объекту параллели со стороны экватора и к ней прибавить число градусов дуги меридиана от этой параллели до объекта. Например, Москва расположена севернее параллели 50°. По меридиану число градусов между этой параллелью и Москвой — 6°, следовательно, географическая широта Москвы — 56° северной широты. Вулкан Везувий находится в северном полушарии и севернее параллели 40°, число градусов между этой параллелью и вулканом — 1°, следовательно, Везувий расположен на 41° северной широты.
Чтобы определить долготу какого-либо объекта, надо найти меридиан, на котором находится этот объект. Например, Санкт-Петербург расположен к востоку от нулевого Гринвичского меридиана, на меридиане, отстоящем от него на 30°, следовательно, долгота Санкт-Петербурга восточная и составляет 30° (в.д).

Рис. 1. С помощью астрономического прибора — секстанта — в Средние века определяли координаты судна в открытом море

Рис. 2. Широта и долгота на глобусе

2. Плоские прямоугольные координаты
Прямоугольная система координат на плоскости образуется двумя взаимно перпендикулярными осями координат Х 1 Х и Y 1 Y (крестом ). Оси координат пересекаются в точке О , которая называется началом координат , на каждой оси выбрано положительное направление.

Положение точки А на плоскости определяется двумя координатами Х и Y .
Ось Х называется осью абсцисс, а ось Y - осью ординат. Координата Х называется абсциссой точки А , координата Y — ординатой точки А .
В правосторонней системе координат положительное направление осей выбирают так, чтобы при направлении оси Y 1 Y вверх, ось Х 1 Х смотрела направо. Обычно принято пользоваться правосторонними системами координат (если обратное не оговорено или не очевидно — например, из чертежа; иногда по каким-то соображениям бывает удобнее всё же пользоваться левосторонней системой координат).
Четыре угла (I, II, III, IV), образованные осями координат Х 1 Х и Y 1 Y , называются координатными углами , четвертями или квадрантами .
Точки внутри координатного угла I имеют положительные абсциссы и ординаты.
Точки внутри координатного угла II имеют отрицательные абсциссы и положительные ординаты.
Точки внутри координатного угла III имеют отрицательные абсциссы и ординаты
Точки внутри координатного угла IV имеют положительные абсциссы и отрицательные ординаты.
3. Полярные и биполярные координаты
Полярные координаты. В войсковой практике они применяются для определения положения одних точек относительно других на сравнительно небольших участках местности, например при целеуказании, засечке ориентиров и целей, составлении схем местности и др.

Рис. 5. Полярные координаты Рис. 6. Биполярные координаты
Система плоских полярных координат (рис. 5 ) состоит из: точки О - начало координат, или полюса, и начального направления ОР , называемого полярной осью. Положение точки М на местности или на карте определяется двумя координатами: углом положения Q , который измеряется по ходу часовой стрелки от полярной оси до направления на определяемую точку М (от 0 до 360°), и расстоянием Д = |ОМ |.
В зависимости от решаемой задачи за полюс принимают наблюдательный пункт, огневую позицию, исходный пункт движения и т.п., а за полярную ось - геодезический меридиан, магнитный меридиан (направление магнитной стрелки компаса) или же направление на какой-либо удаленный ориентир.
Биполярные координаты. Система биполярных (двухполюсных) координат (рис. 6 ) состоит из двух полюсов А и В и общей оси | АВ |, называемой базисом или базой засечки. Положение любой точки М относительно двух данных на карте (местности) точек А и В определяется координатами, которые измеряются на карте или местности Этими координатами могут служить либо два угла положения Q 1 и Q 2 , определяющие направления с точек А и В на искомую точку М , либо расстояния | AM| и | ВМ| до нее. Углы положения, как показано на рис. 6 , измеряются в точках А и В или от направления базиса (т.е. угла А , равного углу ВАМ и угла В , равного углу АВМ ) или углами Qi и Qi .
Биполярные координаты чаще всего используются при наблюдении и засечке целей с пунктов сопряженного наблюдения, нанесении на карту (схему) минных полей и других случаях.
4. Система плоских прямоугольных координат Гаусса-Крюгера
В основу системы координат положена проекция, предложенная немецким ученым К. Гауссом и разработанная для практического применения в геодезии другим немецким ученым — Л. Крюгером. Земной эллипсоид разделен меридианами на равные зоны размером по долготе 6°, простирающиеся от полюса до полюса (рис. 5). Зоны нумеруются с запада на восток от Гринвичского меридиана, который является западной границей первой зоны. Если долготы западного и восточного меридианов, ограничивающих зону, обозначить соответственно через Lз и Lв , а долготу среднего меридиана через L 0 , то по номеру зоны n легко определить их значения по формулам
Lз = 6° (п— 1); Lв = 6 °п; L0 = 6° n —3°.
Средний меридиан зоны называют осевым.
Территория СССР включает 29 зон, начиная с четвертой п тридцать вторую включительно.
Плоские изображения зон получают путем особого проектирования каждой зоны на цилиндр, который разворачивается в плоскость. Представим, что вокруг земного эллипсоида описан цилиндр, ось которого перпендикулярна к оси вращения Земли РР 1 и, следовательно, лежит в плоскости экватора QQ 1 , а касание эллипса с цилиндром происходит по среднему меридиану зоны 3 (рис. 4.7). Зону проектируют с поверхности эллипсоида 2 на поверхность цилиндра 1 . После этого цилиндр разрезается по образующим, на которых лежат точки Р и P 1 , и полуцилиндр разворачивается в плоскость. Поворачивая цилиндр последовательно вокруг оси РР 1 на 6°, проектируют последовательно все остальные зоны.
Проектирование эллипсоида на цилиндр выполняется с соблюдением следующих трех условий:
1) изображение на плоскости должно быть равноугольным (подобным), иначе говоря, углы фигур, построенных на поверхности эллипсоида, изображаются на плоскости без искажений;
2) осевой (средний) меридиан зоны и экватор изображаются взаимно перпендикулярными прямыми;
3) масштаб изображения вдоль осевого меридиана должен быть равен единице. Это означает, что длины дуг, расположенных на осевом меридиане, переносятся
на плоскость без искажений. Масштаб изображения увеличивается при удалении от осевого меридиана к границам зоны.

Изображение зоны на плоскости получается несколько более широким, чем на эллипсоиде.
В результате проектирования получаем изображение каждой зоны в проекции на плоскость.
В каждой зоне (рис. 4.7) изображение осевого меридиана принимается за ось абсцисс х , а изображение экватора — за ось ординат у. Началом координат в каждой зоне служит точка пересечения осевого меридиана и экватора. Абсциссы отсчитываются от экватора к северу и югу, ординаты — от осевого меридиана к западу и востоку. К северу от экватора абсциссы положительные, к югу — отрицательные. Ординаты к востоку от осевого меридиана имеют знак
плюс, к западу — минус. В северном полушарии абсциссы всегда положительны. Ординаты же могут быть положительными и отрицательными. Чтобы не иметь отрицательных ординат, в практике ординату осевого меридиана принимают равной 500 км, как это показано на рис 4.7. Исправленную указанным образом ординату называют преобразованной. Для однозначного определения положения точки на земной поверхности перед каждой ординатой ставится номер
зоны. Поэтому, если ординаты относительно осевого меридиана 12 зоны равны +36785,15 м и —24076,11 м, то преобразованные ординаты тех же точек будут: у 1 = 12536785,15 м и у 2 =
Для облегчения работы на листах карт наносится координатная сеть квадратов, образованных линиями, параллельными изображениям осевого меридиана (ось х) и экватора зоны (ось у).
Положение точки на поверхности сферы определяется двумя сферическими координатами – широтой и долготой ( рисунок 2.1).
точка О – центр сферы;
точка Р – северный полюс;
точка Р' – южный полюс.
Проведем линию экватора QQ, полученную от пересечения плоскости экватора и поверхности сферы.
Рисунок 2.1 – Астрономические координаты
Плоскость меридиана точки А, лежащей на поверхности сферы, проходит через отвесную линию точки А и ось вращения Земли РР'. Меридиан точки А – это линия пересечения плоскости меридиана точки А с поверхностью сферы.
Широта точки А – это угол, образованный отвесной линией точки А и плоскостью экватора. Этот угол лежит в плоскости меридиана точки.
Широта отсчитывается в обе стороны от экватора (к северу – северная широта, к югу – южная) и изменяется от 0° до 90°.
Долгота точки А – двухгранный угол между плоскостью начального меридиана и плоскостью меридиана точки А. Начальный меридиан проходит через центр главного зала Гринвичской обсерватории, расположенной вблизи Лондона. Долготы изменяются от 0° до 180°, к западу от Гринвича – западные и к востоку – восточные. Все точки одного меридиана имеют одинаковую долготу.
Проведем через точку А плоскость, параллельную плоскости экватора; линия пересечения этой плоскости с поверхностью сферы называется параллелью точки; все точки параллели имеют одинаковую широту.
Проведем плоскость G, касательную к поверхности сферы в точке А; эта плоскость называется плоскостью горизонта точки А. Линия пересечения плоскости горизонта и плоскости меридиана точки называется полуденной линией; направление полуденной линии – с юга на север. Если провести полуденные линии двух точек, лежащих на одной параллели, то они пересекутся в точке на продолжении оси вращения Земли РР' и образуют угол g, который называется сближением меридианов этих точек.
Широту и долготу точек местности определяют из астрономических наблюдений, потому они и называются астрономическими координатами.
2.2 Геодезические координаты

На поверхности эллипсоида вращения положение точки определяется геодезическими координатами – геодезической широтой В и геодезической долготой L на рисунке 2.2.
Геодезическая широта точки – это угол, образованный нормалью к поверхности эллипсоида в этой точке и плоскостью экватора.
Геодезическая долгота точки – это двухгранный угол между плоскостью
начального меридиана и плоскостью
Рисунок 2.2 - Геодезические координаты
Плоскость геодезического меридиана проходит через точку А и малую полуось эллипсоида; в этой плоскости лежит нормаль к поверхности эллипсоида в точке А. Геодезическая параллель получается от пересечения поверхности эллипсоида плоскостью, проходящей через точку А и параллельной плоскости экватора.
Различие геодезических и астрономических координат точки А зависит от угла между отвесной линией данной точки и нормалью к поверхности эллипсоида в этой точке. Этот угол называется уклонением отвесной линии; он обычно не превышает 5''. В некоторых районах Земли, называемых аномальными, уклонение отвесной линии достигает нескольких десятков дуговых секунд. При геодезических работах невысокой точности астрономические и геодезические координаты не различают; их общее название – географические координаты.
Две координаты – широта и долгота - определяют положение точки на поверхности относимости (сферы или эллипсоида).
Для определения положения точки в трехмерном пространстве нужно задать ее третью координату, которой в геодезии является высота. В нашей стране счет высот ведется от уровенной поверхности, соответствующей среднему уровню Балтийского моря; эта система высот называется Балтийской.
2.3 Прямоугольные координаты
Систему плоских прямоугольных координат образуют две взаимно перпендикулярные прямые линии, называемые осями координат; точка их пересечения называется началом или нулем системы координат. Ось абсцисс – 0Х, ось ординат – 0Y ( рисунок 2.3).
Существует две системы прямоугольных координат: левая и правая. В геодезии чаще применяется левая система. Положение точки в прямоугольной системе координат однозначно определяется двумя координатами Х и Y; координата Х выражает расстояние точки от оси ОY, а координата Y – расстояние от оси ОХ.
Рисунок 2.3 – Прямоугольные координаты
2.4 Полярные координаты
Систему полярных координат образует направленный прямой луч ОХ. Начало координат – точка 0 – называется полюсом системы, линия ОХ – полярной осью (рисунок 2.4).
Положение любой точки в полярной системе определяется двумя координатами: радиус-вектором r (синоним – полярное расстояние S) – расстоянием от полюса до точки, и полярным углом при точке 0, образованным осью ОХ и радиус-вектором точки и отсчитываемым от оси ОХ по ходу часовой стрелки.
Рисунок 2.4 – Полярные координаты
Переход от прямоугольных координат к полярным и обратно для случая, когда начала обеих систем находятся в одной точке, и оси ОХ у них совпадают, выполняется по формулам:
Эти формулы получаются из решения DОВА по известным соотношениям между сторонами и углами прямоугольного треугольника.
Системы прямоугольных и полярных координат применяются в геодезии для определения положения точек на местности.
Положение точек на земной поверхности может быть определено в различных системах координат.
Системы географических и геодезических координат. Система географических координат является единой системой для всех точек Земли. При этом уровенная поверхность принимается за поверхность сферы. За начало отсчета в географической системе координат принимают начальный меридиан РМ0Р1 , проходящий через центр Гринвичской обсерватории на окраине Лондона и плоскость экватораЕQ (рисунок 1.2)
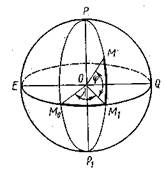 |
Рисунок 1.2 – Географическая система координат
Угол φ,называемый географической широтой, отсчитывается от плоскости экватора к северу и к югу от 0 до 90˚. Широты точек, расположенных в северном полушарии, называют северными, а в южном – южными.
Угол λ, называемый географической долготой, отсчитывается от плоскости начального меридиана к востоку и западу от0 до 180˚. Точки, расположенные восточнее начального меридиана, имеют восточные долготы, а западнее – западные.
Зональная система прямоугольных координат Гаусса. Чтобы установить связь между географическими координатами любой точки на плоскости, применяют способ проектирования поверхности земного шара на плоскость по частям, которые называются зонами.
В такой системе начало координат для всех зон принимается в точке пересечения осевого меридиана данной зоны с экватором. Координатными осями являются соответственно ось абсцисс и ось ординат (рисунок 1.3)
 |
Рисунок 1.3 – Зональная система координат
Абсциссы, отсчитываемые от экватора к северному полюсу, считаются положительными, на запад – отрицательными. Точка А1 (рисунок 1.3) будет иметь координаты: абсциссу ха и ординату уа.
Система прямоугольных координат.В геодезической практике часто положение точек определяют плоскими прямоугольными координатами. В этой системе плоскость координат совпадает с плоскостью горизонта в данной точке О, являющейся началом этих координат; ось х всегда направлена на север, а ось у – на восток. Северное направление оси абсцисс считается положительным (+), южное – отрицательным (-); направление оси ординат считается положительным на восток и отрицательным на запад.
Оси координат делят плоскость чертежа на четыре части, которые называются четвертями: I – СВ, II – ЮВ, III – ЮЗ, IV – СЗ (рисунок 1.4)
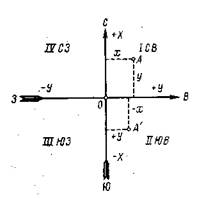 |
Рисунок 1.4 – Система прямоугольных координат.
Полярная система координат.В полярной системе координат (рисунок 1.5) положение любой точки А на плоскости определяется радусом-вектором r, исходящим из точки О, называемой полюсом, и углом β, отсчитываемым по ходу часовой стрелки от линии ОХ – полярной оси – до радиуса-вектора.
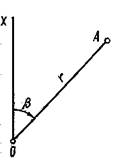 |
Рисунок 1.5 – Полярная система координат
Абсолютные и условные высоты. Спроектируем точку А (рисунок 1.6) физической поверхности Земли по направлению отвесной линии на уровенную поверхность. Высота НА этой точки, измеряемая от уровня моря, называется абсолютной, а Н', измеряемая от произвольной уровенной поверхности, - условной. Относительной высотой точки или превышением называется высота ее над другой точкой земной поверхности, она обозначается через h. Например, превышение точки А над точкой В составит hА = НА – НВ. Для определения высоты уровня моря на его берегу надежно закрепляют в вертикальном положении рейку с делениями – футшток и периодически фиксируют уровень моря относительно этой рейки.
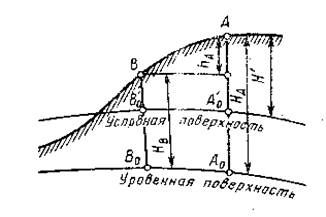 |
Рисунок 1.6 – Абсолютные и условные отметки
В РФ высоты точек физической поверхности Земли отсчитываются от нуля Кронштадского футштока (черта на медной доске, установленной в гранитном устое моста через Обводной канал в Кронштадте).
Числовые значения высот точек называют отметками.
Контрольные вопросы
1. Что такое физическая и уровенная поверхность Земли?
2. Что называется географической широтой и долготой?
3. Какие системы координат применяются в геодезии?
4. Что называется абсолютной и условной высотой точки на земной поверхности?
5. Что называется относительной высотой точки на земной поверхности?
6. Что называется отметкой точки на земной поверхности?
ЛЕКЦИЯ №2
УРОК №2. МАСШТАБЫ ТОПОГРАФИЧЕСКИХ ПЛАНОВ И КАРТ. УСЛОВНЫЕ ЗНАКИ.
Понятие о геодезических планах и картах
Планом местности называется чертеж, представляющий собой уменьшенное и подобное изображение ее проекции на горизонтальную плоскость.
На плане длины линий, углы и площади контуров участков местности не искажаются, а степень уменьшения ее линейных элементов (масштаб изображения) постоянна для всех частей плана. Планы, на которых изображена только ситуация местности, называются ситуационными или контурными. Планы, на которых кроме предметов местности изображен еще и рельеф, называют топографическими.
Картой называется построенное по определенным математическим законам уменьшенное обобщенное изображение на плоскости всей Земли или значительных ее частей с учетом кривизны уровенной поверхности.
Карты в зависимости от масштабов условно делят на крупномасштабные – 1: 100000 и крупнее, среднемасштабные – от 1: 200000 до 1: 1000000, мелкомасштабные – мельче 1: 1000000.
При выполнении геодезических работ, входящих в комплекс строительно-монтажного производства, для составления планов применяют масштабы 1 : 200, 1 : 500, 1 : 1000, 1 : 2000, 1 : 5000.
Профилем местности называется изображенное в уменьшенном виде сечение вертикальной плоскостью поверхности Земли по заданному направлению. Профили местности используют для строительства и монтажа надземных и подземных инженерных сооружений и сетей.
Топографические планы применяют в основном для строительного проектирования. На таком плане изображают весь комплекс подземных и надземных сооружений. В зависимости от размеров и назначения строительства его рабочий проект составляют в масштабе 1 : 500 – 1 : 1000, на отдельные объекты в зависимости от их сложности – в масштабе 1 : 200 и крупнее.
Масштабы
Масштабом называется отношение длин линии на плане (профиле) к соответствующей проекции этой линии на местности. Следовательно, масштаб есть число отвлеченное – правильная дробь. Для удобства пользования и сравнения все масштабы имеют однообразный вид: числителем дроби всегда является единица; при этом знаменатель непосредственно выражает степень уменьшения
Численный масштаб – масштаб, где числитель выражен единицей.
S0 / S = 1 / S:S0 = 1/М(1)
В формуле (1) М – знаменатель численного масштаба, который показывает, во сколько раз были уменьшены проложения линий местности при изображении их на плане. Из численного масштаба следует, что определенной единице длины на плане соответствует 1000 или 2000 или 5000 и т.д. таких же единиц на местности. Например, 1см на разных планах или картах соответствует 1000, 2000, 50000, 10 000см на местности или в переводе на метры 10, 20, 50 и 100м.
При сравнении двух масштабов более крупным называют тот, у которого знаменатель меньше. Естественно, чем крупнее масштаб, тем больше подробностей может быть изображено на плане или карте. Планы, на которых должно быть показано больше подробностей, следует составлять в более крупном масштабе.
Читайте также:

