Методы линеаризации кинетической кривой лайнуивера берка иди хофсти и др реферат
Обновлено: 05.07.2024
Линеаразиция - один из наиболее распространенных методов анализа нелинейных систем. Идея линеаризации - использование линейной системы для аппроксимации поведения решений нелинейной системы в окрестности точки равновесия.
Линеаризация позволяет выявить большинство качественных и особенно количественных свойств нелинейной системы.
Методы линеаризации имеют ограниченный характер, то есть эквивалентность исходной нелинейной системы и ее линейного приближения сохраняется лишь для ограниченных пространственных или временных масштабов системы, или для определенных процессов, причем, если система переходит из одного режима работы в другой, то следует изменить и ее линеаризованную модель.
Линеаризация нелинейных динамических систем методом замены переменных
Линеаризация системы нелинейных уравнений в окрестности точки равновесия может быть достигнута путем замены переменных так, чтобы точка равновесия превратилась в начало координат.
Уравнения, полученные в результате указанного действия, будут линейными и называться линеаризацией исходной системы. Точки исходной системы, находящиеся в окрестности точки равновесия, будут соответствовать точкам в окрестности начала координат новой системы. Нас будет интересовать:
- значение новых переменных, близкие к нулю;
- при каких условиях нелинейными выражениями можно пренебречь.
Рассмотрим нелинейную систему: (1) что имеет точки равновесия (p, q). Преобразование u=x-p v=y-q переводит точки равновесия p, q в начало координат. Дифференцирование дает: (2) После замены переменных, подставив их новые значения в каждое уравнение, выделим линейную часть: где F(u,v) и G(u,v) и состоят только из нелинейных выражений. Говорят, что линейная система есть линерализацией системы (1) при таких условиях: Эти последние условия обеспечивают то, что нелинейные выражения F(u,v) и G(u,v) на столько малы по сравнению с u и v при приближении к точке равновесия, что ими можно пренебречь.
Линеаризация на основе якобиана

Замену переменных можно использовать и при другой организации линеаризации. Производят замену: где Это может быть записано в виде: где называется якобиан.
Константу Михаэлиса можно определить из графика Михаэлиса (рис.2.2.1), найдя графическим способом максимальную скорость и соответствующую величину концентрации субстрата, при которой скорость ферментативной реакции будет вдвое меньше Vmax. Эта величина [S] и будет Км. Таким способом можно определить только приблизительную величину константы Михаэлиса из-за трудности точного графического определения Vmax.
Более удобными являются методы, в которых осуществлена линеаризация уравнения Михаэлиса-Ментен, т. е. гиперболическая зависимость v от [S] переведена в линейную.
Для того чтобы построить такой график, необходимо определить в одинаковых условиях при различных концентрациях субстрата и [E]= const начальные скорости ферментативной реакции.
Метод Лайнуивера-Берка. Один из способов линеаризации уравнения Михаэлиса-Ментен предложили Лайнуивер и Берк (Lineweaver H., Burk D.). Это так называемый метод двойных обратных величин. Для линеаризации необходимо взять обратные величины от левой и правой частей уравнения (3), в результате чего оно преобразуется в уравнение вида,
согласно которому между величинами, обратными начальной скорости (1/v, v -1 ) и концентрации субстрата (1/[S], [S] -1 ) соблюдается линейная зависимость, если механизм реакции подчиняется изложенным выше представлениям (рис.2.2.3).
Рис. 2.2.3. График зависимости 1/v от 1/[S] (график Лайнуивера-Берка)
Экспериментальная прямая пересекает ось абсцисс в точке (-1/[S] = 1/Км), а ось ординат – в точке (1/v = 1/Vмах). Тангенс угла наклона равен Км/Vмах. Этим широко пользуются для определения параметров Км и Vмах, характеризующих связывающую и каталитическую функции ферментов.
Метод Хайнса-Вульфа. В этом случае преобразуется уравнение Лайнуивера-Берка путем умножения правой и левой частей на концентрацию субстрата.

Графическая зависимость приведена на рис.2.2.4.
Рис. 2.2.4. График зависимости [S]/v от [S] (график Хайнса-Вульфа)
Это прямая с наклоном 1/Vmax, отсекающая на осях [S]/v и [S] отрезки Км/ Vmax и – Км соответственно.
Метод Иди-Хофсти. При одном из таких графических преобразований в так называемом графике Иди-Хофсти(pиc.2.2.5) строят график зависимости v от v/[S]. В этом случае точка пересечения прямой, полученной путем наилучшей линейной аппроксимации экспериментальных точек, с осью ординат соответствует Vmax, а тангенс угла наклона равен – Km. Данный способ линеаризации приведен на рис. 2.2.5.
Рис. 2.2.5. График зависимости v от v/[S] (график Эди-Хофсти)
Метод Эйзенталя и Корниш-Боудена. Много позднее Эйзенталь и Корниш-Боуден предложили иной метод графического представления результатов исследования кинетики ферментативных реакций – так называемый прямой линейный график. Уравнение Михаэлиса-Ментен они преобразовали в виде зависимости Vmax от Км:
Для любой пары значений [S] и v можно построить зависимость Vmax от Км. Она представляет прямую с наклоном, равным v/[S], и отрезками, отсекаемыми на осях Км и Vmax, соответственно равными -[S] v. Если провести прямые для нескольких пар значений [S] и v, то эти прямые пересекутся в одной точке, координаты которой дадут единственные значения Vmax от Км, удовлетворяющие всем парам значений [S] и v (рис.2.2.6).
Преимущества такого графика очевидно: для его построения не требуется никаких расчетов, он позволяет очень просто выявить ошибочные данные (иакие прямые будут выпадать из основной совокупности прямых).
Уравнение Михаэлиса лежит в основе всех кинетических исследований ферментативных реакций, так как оно позволяет рассчитать количественные характеристики ферментов и проводить анализ их ингибирования. Величины Кm и Vmax являются важнейшими характеристиками ферментов и их можно определить, используя линеаризованные формы уравнения Михаэлиса-Ментен.
В заключении необходимо отметить, что графические методы для определения V и Кm не являются оптимальными. В настоящее время данные ферментативной кинетики обрабатывают быстрее и более объективно с помощью компьютерных программ.
Процессы, приводящие к денатурации фермента, могут иметь различную физико-химическую природу. Конформация белковой молекулы в растворе зависит от двух показателей – величины рН и температуры. Повышение температуры приводит к нарушению системы слабых связей, стабилизирующих белковую молекулу. Длительное воздействие повышенной температуры приводит к необратимым изменениям структуры фермента, сопровождающимся потерей активности (тепловая денатурация).
Каждый фермент характеризуется соответствующим зарядом, создаваемым ионогенными группами аминокислотных остатков. При очень низких или высоких значениях рН изменение степени ионизации функциональных групп может приводить к необратимым нарушениям нативной конформации молекулы фермента с разрушением структуры активного центра.
Конформационные изменения в белковой молекулу сопровождаются изменениями спектров поглощения и флуоресценции ароматических аминокислот – тирозина и триптофана в ультрафиолетовой области спектра (~ 290 нм), что позволяет отслеживать изменения в структуре фермента. Обратимые конформационные, вызванные изменением температуры или концентрацией протонов водорода, осуществляются в течение 10 -4 – 10 -1 с, необратимые денатурационные изменения в зависимости от условий – в течение 1-10 3 мин. Более подробный анализ кинетики денатурации ферментов рассмотрен в Теме 5 учебного пособия по самостоятельной работе.
Vmax = k2[Е]0. Кинетическая константа k2 называется числом оборотов.
Величины k2 для различных ферментов
Число оборотов/cек
Число оборотов фермента - это то количество молекул субстрата, которое превращается в продукт реакции в единицу времени при полном насыщении фермента субстратом. Другими словами, это мера эффективности работы фермента. Самым активным из известных ферментов является карбоангидраза
Методы определения величин КМ и Vmax. Кинетические константы односубстратной реакции определяют путем измерения скорости реакции при различных концентрациях субстрата (S). Наиболее удобный способ для их расчета - это линеаризация уравнения Михаэлиса–Ментен, графические методы определения константы КМ и Vmax. Ниже представлены графики Лайнуивера-Берка и Иди-Хофсти.
Ниже представлен график Лайнуивера–Берка.
Далее приведен график Иди–Хофсти.
Ниже представлен график Эйзенталя–Корниш-Боудена.
Ингибирование и активация ферментов. Эффекторы - соединения, специфично влияющие на скорость ферментативных реакций. Одни из них ускоряют процесс и называются активаторами, другие замедляют и носят название ингибиторов ферментов. По принципу действия ингибиторы делят на обратимые и необратимые.
Обратимое ингибирование. Конкурентный ингибитор структурно подобен субстрату и потому связывается в активном центре фермента, вследствие чего препятствует связыванию субстрата в том же центре (см. ниже рисунок). Конкурентный ингибитор уменьшает скорость реакции, снижая долю молекул фермента, связавших субстрат. Неконкурентный ингибитор и субстрат могут связываться молекулой фермента одновременно, т. е. участки их связывания не перекрываются. Неконкурентный ингибитор уменьшает число оборотов фермента, а не снижает долю связавших субстрат молекул фермента.
Конкурентное и неконкурентное ингибирование различаются по кинетике.
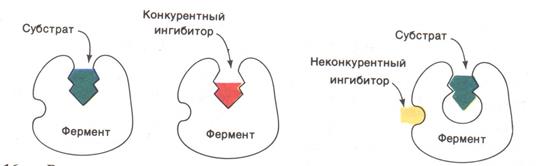
Далее приведена схема конкурентного ингибирования.
Отличительной особенностью конкурентного ингибирования является способность субстрата при достаточно высокой концентрации (~ 5–10 Км) предотвращать ингибирование, другими словами, защищать фермент.

где оператор Lотображает банахово пространство Нв себя, L(0)=0, и дифференцируем по Фреше. Одним из классич. методов решения (1), связанным с линеаризацией (1), является итерационный метод Ньютона - Канторовича, в к-ром при известном приближении и n новое приближение и n+ 1 определяется как решение линейного уравнения

основой метода служит аппроксимация (при малых ) выражением - производная Фреше оператора Lв точке и n . Различные модификации этого метода и соответствующие оценки скорости сходимости могут быть найдены в [1] - [4]. Само операторное уравнение (1) может соответствовать, напр., нелинейной краевой задаче для уравнения с частными производными (см. [2], [4], [5]), и тогда на каждом шаге в (2) должна решаться линейная краевая задача, что вызывает необходимость применения численных методов и той или иной дискретизации исходной задачи и родственных ей линейных задач. С вычислительной точки зрения более естественно рассматривать методы линеаризации после соответствующей дискретизации исходной задачи, считая (1) операторным уравнением в конечномерном пространстве.
Другим примером Л. м. для приближенного решения (1) может служить итерационный метод секущих (ложного положения) (см. [2], [3]). Во многих случаях для задач (1), являющихся задачами математич. физики, линеаризацию предпочитают проводить на основе физич. соображений, заменяя на с линейным оператором (см. [5] - [11]).
Тогда получаемые итерационные методы записываются в виде


Таковы, напр., методы упругих решений и переменных параметров для решения нелинейных задач теории упругости (см. [5] - [8]); при этом для метода упругих решений линейный оператор соответствует оператору линейной теории упругости. К ним же примыкают итерационный метод Качанова (см. [9], [10]) и метод последовательных нагружений (см. [6] - [8]), сочетающий в себе идеи линеаризации и продолжения по параметру. Иногда вместо методов (3) используются более общие итерационные методы типа


с итерационным параметром подлежащим выбору. При реализации упомянутых методов следует учитывать и приближенность решения систем (напр., как следствие применения вспомогательных итерационных методов) (см., напр., [1], [12], [13]). При рассмотрении нелинейных задач на собственные значения (задач нахождения точек бифуркации), напр. вида

идея линеаризации (5), сводящая исследование задачи (5) к исследованию линейной задачи на собственные значения


оказалась весьма плодотворной (см. [14] - [16]). Часто используется та или иная линеаризация и в сеточных методах решения нестационарных нелинейных задач (см., напр., [17] - [21] ), проводимая за счет известных решений в моменты времени до t n и дающая линейные уравнения для решения в следующий дискретный момент (t - шаг по времени). Лит.:[1] Красносельский М. А. [и др.], Приближенное решение операторных уравнений, т. 1, М., 1969 ; [2] К о л л а т ц Л., Функциональный анализ и вычислительная математика, пер. с нем., М., 1969; [3] О р т е г а Д ж., Р е й н б о л д т В., Итерационные методы решения нелинейных систем уравнений со многими неизвестными, пер. с англ., М., 1975; [4] Б е л л м а н Р., К а л а б а Р., Квазилинеаризация и нелинейные краевые задачи, пер. с англ., М., 1968; [5] П о б е д р я Б. Б., в кн.: Упругость и неупругость, в. 3, М., 1973, с. 95-173; [6] О д е н Д ж., Конечные элементы в нелинейной механике сплошных сред, пер. с англ., М., 1976; [7] Зенкевич О., Метод конечных элементов в технике, пер. с англ., М., 1975; [8] С в и р с к и й И. В., Методы типа Бубнова - Галеркияа и последовательных приближений, М., 1968; [9] М и х л и н С. Г., Численная реализация вариационных методов, М., 1966; [10] Futik S., Kratochvil A., Necas I., "Acta Univ. Corolinae. Math, et Phys.", 1974, v. 15, № 1-2, p. 31-33; [11] Амосов А. А., Бахвалов Н. С., О с и-п и к Ю. И.; "Ж. вычисл. матем. и матем. физики", 1980, т. 20, № 1, с. 104-11; [12] Е i s е n s t a t S. С., S с h u l t z М. Н., S h е r m a n А. Н., "Lect. Notes Math.", 1974, № 430, p. 131 - 53; [13] Дьяконов Е. Г., в кн.: Численные методы механики сплошной среды, т. 7, № 5, М., 1976, с. 14-78; [14] В о р о в и ч И. И., в кн.: Проблемы гидродинамики и механики сплошной среды. К шестидесятилетию акад. Л. И. Седова, М., 1969; [15] Бергер М. С., в кн.: Теория ветвления и нелинейные задачи на собственные значения, пер. с англ., М., 1974, с. 71-128; [16] Скрыпник И. В., Нелинейные эллиптические уравнения высшего порядка, К., 1973; [17] Ладыженская О. А., Математические вопросы динамики вязкой несжимаемой жидкости, 2 изд., М., 1970; [18] Дьяконов Е. Г., Разностные методы решения краевых задач, в. 2 - Нестациопарные задачи, М., 1972; [19] Р и в к и н д В. Я., У р а л ь ц е в а Н. Н., в кн.: Проблемы математического анализа, в. 3, Л., 1972, с. 69-111; [20] Fairweather G., Finite element Galerkin methods for differential equations, N. Y., 1978. [Led. Notes pure and appl. math., v. 34]; [21] L u s k i n M., "SIAM J. Numer. Analysis", 1979, v. 16, № 2, p. 284-99.
Е. Г. Дьяконов.
Математическая энциклопедия. — М.: Советская энциклопедия . И. М. Виноградов . 1977—1985 .
Читайте также:

