Квадрат и ромб реферат

Обновлено: 05.07.2024

В этом уроке мы рассмотрим такие геометрические фигуры, как ромб и квадрат. Введем понятие ромба. Узнаем, какими свойствами обладают диагонали ромба. Рассмотрим 2 признака ромба. Закрепим представления о квадрате. Вспомним основные свойства квадрата. И, конечно же, закрепим изученный материал в практической части урока.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.

Получите невероятные возможности

Конспект урока "Ромб и квадрат"

Давайте ещё раз вспомним, что параллелограмм – это четырёхугольник, у которого противоположные стороны попарно параллельны. А прямоугольник – это параллелограмм, у которого все углы прямые.

На этом уроке мы поговорим о таких геометрических фигурах как ромб и квадрат.

Итак, ромб – это параллелограмм, у которого все стороны равны.

Так как ромб является параллелограммом, то он обладает всеми его свойствами, о которых мы с вами говорили на предыдущих уроках.

Теорема. Свойства диагоналей ромба. У ромба диагонали взаимно перпендикулярны и лежат на биссектрисах его углов.

Доказательство.

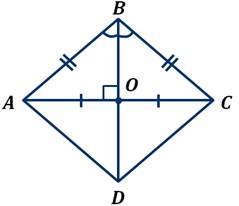
Рассмотрим .

, следовательно, – медиана.

– равнобедренный.

Медиана – биссектриса, высота.

Следовательно, диагональ и лежит на биссектрисе .

Что и требовалось доказать.

Теперь сформулируем и докажем признаки ромба.

Теорема. Признак ромба. Если у параллелограмма диагонали взаимно перпендикулярны, то этот параллелограмм – ромб.

Доказательство.

Рассмотрим и .

Сторона – общая, , так как диагонали т. делятся пополам

по двум катетам.

Следовательно, .

, .

Следовательно, .

– ромб.

Что и требовалось доказать.

И ещё один признак.

Теорема. Признак ромба. Если у параллелограмма одна из диагоналей лежит на биссектрисе угла, то этот параллелограмм – ромб.

Доказательство.

как накр. лежащие при и секущей .

Следовательно, .

– равнобедренный, то есть .

Следовательно, .

– ромб.

Что и требовалось доказать.

Задача. Чему равны углы ромба, если его меньшая диагональ равна стороне?

– равносторонний.

Ответ: , , , .

Решим ещё одну задачу.

Задача. В ромбе перпендикуляр , проведённый из вершины делит сторону пополам. Найдите градусную меру .

– прямоугольный.

, то есть .

, – внутр. одностор. при и секущей .

Так как , то .

Ответ: .

Теперь поговорим о квадрате.

Квадрат – это прямоугольник, у которого все стороны равны. Также можно сказать, что квадрат – это ромб, у которого все углы прямые.

Эти два определения равносильны. Из каждого следует, что квадрат – это параллелограмм, который одновременно является и прямоугольником, и ромбом.

Следовательно, квадрат обладает всеми свойствами и прямоугольника, и ромба.

Основные свойства квадрата:

1.Все углы квадрата прямые.

2. Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и лежат на биссектрисах его углов.

Задача. На рисунке – квадрат, . Найдите .

, – смежные, то есть .

Так как , то .

– равнобедренный, тогда .

Вы можете изучить и скачать доклад-презентацию на тему Прямоугольник. Ромб. Квадрат. Презентация на заданную тему содержит 13 слайдов. Для просмотра воспользуйтесь проигрывателем, если материал оказался полезным для Вас - поделитесь им с друзьями с помощью социальных кнопок и добавьте наш сайт презентаций в закладки!

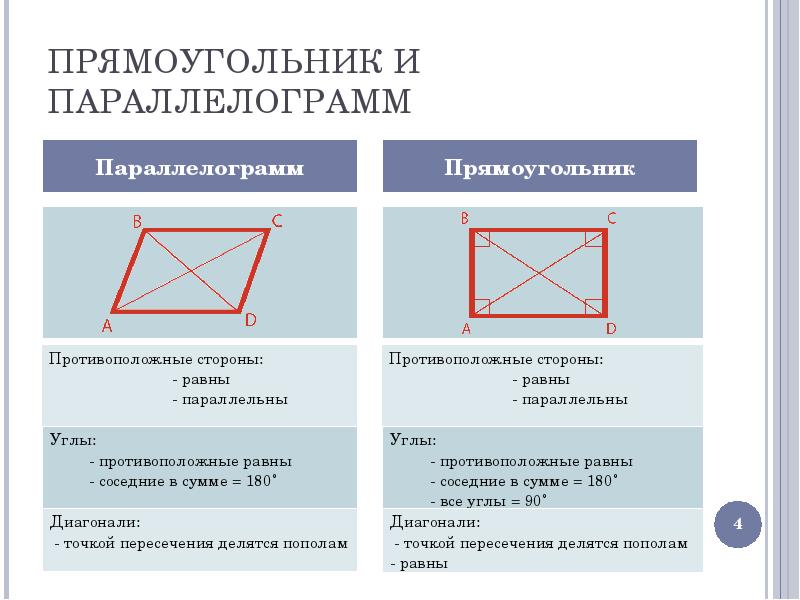
ЦЕЛИ УРОКА: Повторить понятие параллелограмма; Дать определение прямоугольника, ромба, квадрата. Познакомиться со свойствами данных фигур; Научиться применять свойства при решении задач.

ПРИЗНАК ПРЯМОУГОЛЬНИКА Вопрос: любой четырехугольник, в котором диагонали равны, является прямоугольником? Ответ: не всегда

СВОЙСТВА РОМБА 1. Противоположные стороны попарно параллельны: AB//CD, AD//BC 2. Все стороны равны: AD=DC=CB=AB 3. Противоположные углы равны: ∟A=∟C, ∟D=∟B 4. Соседние углы в сумме дают 180˚: ∟A+∟B=180˚, ∟C+∟D=180˚ 4. Диагонали ромба пересекаются под прямым углом: AC ┴ BD 5. Диагонали ромба точкой пересечения делятся пополам: AО=CО, ОB =DО

СВОЙСТВА КВАДРАТА 1. Все стороны равны 2. Все углы прямые 3. Диагонали равны 4. Диагонали точкой пересечения делятся пополам 5. Диагонали пересекаются под прямым углом

ПРИЗНАКИ КВАДРАТА Если в прямоугольнике диагонали перпендикулярны – это квадрат Если в ромбе диагонали равны – это квадрат Если в параллелограмме диагонали перпендикулярны и равны – это квадрат

Равенства. Неравенства. Знаки" width="120" src="https://myslide.ru/documents_2/9470990cdd1ac60ec110d2e3b281836e/thumb.jpg" original="/documents_2/9470990cdd1ac60ec110d2e3b281836e/thumb.jpg">

99351 99359 99367 99372 99356 99361 99370 99357 99369 99346 99373 99347 99349 99362 99368 99355 99364 99348 99360 99350 99352 99358 99365 99354 99344 99353 99371 99345 99366 99363

Обратная связь

Если не удалось найти и скачать доклад-презентацию, Вы можете заказать её на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Мы в социальных сетях

В данной публикации мы рассмотрим определение, свойства и признаки (с рисунками) одной из основных геометрических фигур – ромба.

Определение ромба

Ромб – это фигура на плоскости; разновидность параллелограмма, у которого все четыре стороны равны и попарно параллельны. Обычно ромб обозначается названиями его вершин (например, ABCD), а длина его стороны – строчной латинской буквой (например, a).

Примечание: квадрат является частным случаем ромба.

Свойства ромба

Свойство 1

Противоположные углы ромба равны между собой, а сумма соседних углов составляет 180°.

Свойство 2

Диагонали ромба пересекаются под прямым углом и в точке пересечения делятся пополам.

В результате пересечения диагоналей ромб делится на 4 прямоугольных треугольника: ΔAEB, ΔBEC, ΔAED и ΔDEC.

Свойство 3

Диагонали ромба являются биссектрисами его углов.

Свойство 4

Сторону ромба a можно найти через его диагонали d₁ и d₂ (согласно теореме Пифагора).

Свойство 5

В любой ромб можно вписать окружность, центр которой лежит на пересечении его диагоналей.

Радиус вписанной в ромб окружности r вычисляется по формуле:

Признаки ромба

Параллелограмм является ромбом только в том случае, если для него верно одно из следующих утверждений:

Его диагонали пересекаются под прямым углом.
Если его диагонали являются биссектрисами его углов.
Две смежные стороны равны (следовательно, все стороны равны).

Примечание: Любой четырехугольник, стороны которого равны, является ромбом.

Ромб – это частный случай параллелограмма, поэтому он обладает всеми свойствами параллелограмма. Однако есть и специфические свойства, о которых пойдёт речь. Но для начала сформулируем одно из определений ромба.

Ромб – это параллелограмм, у которого все стороны равны.

Сформулируем и докажем теорему о свойствах ромба.

Теорема

Диагонали ромба перпендикулярны и делят углы ромба пополам (являются биссектрисами углов) (см. Рис. 1).

Дано:

– ромб

Доказать:

Доказательство:

Рассмотрим : – середина (так как ромб является параллелограммом, то его диагонали в точке пересечения делятся пополам). Кроме того, из определения ромба следует, что . Значит, треугольник – равнобедренный; является медианой этого треугольника, проведённой к основанию, а, значит, и биссектрисой, и высотой. Из этого следует, что:

, то есть диагонали ромба перпендикулярны;

, то есть диагонали ромба являются биссектрисами его углов (равенство остальных углов можно доказать аналогично).

Ещё один частный случай параллелограмма – квадрат.

2. Квадрат и его свойства

Квадрат – это прямоугольник, у которого все стороны равны.

Квадрат обладает всеми свойствами прямоугольника и ромба. А именно:

· все углы квадрата прямые;

· диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делят углы квадрата пополам.

3. Задачи на ромб и квадрат

Теперь рассмотрим несколько задач, в которых встречаются ромб и квадрат.

Задача 1.

В ромбе одна из диагоналей равна стороне (см. Рис. 2). Найти:

б) углы между диагоналями и сторонами.

Дано: – ромб; .

Найти: а) ; б) .

а) (так как у ромба все стороны равны). Значит, треугольник – равносторонний. Отсюда следует, что угол . Так как в любом параллелограмме сумма соседних углов равна , то .

Ответ: .

б) По доказанной выше теореме: . Аналогично получаем, что .

Ответ: .

Задача 2.

Найти периметр ромба , в котором , а меньшая диагональ равна . Найти периметр ромба.

Дано: – ромб; .

Найти:

Рассмотрим треугольник , в нём: . Значит, данный треугольник равнобедренный, угол при вершине у него равен , два других угла при основании равны, поэтому данный треугольник – равносторонний. Значит: . Так как в ромбе все стороны равны, то периметр ромба равен: .

Ответ: .

Задача 3.

Найдите углы, которые образуют диагонали ромба с его сторонами, если один из углов ромба равен .

Дано: – ромб, .

Найти:

Вспомним, что в любом параллелограмме противоположные углы, а сумма углов, прилежащих к одной стороне, равна . Из этого следует, что: . Теперь воспользуемся доказанной вначале теоремой: .

Ответ:

Задача 4.

Докажите, что параллелограмм является ромбом, если:

а) его диагонали взаимно перпендикулярны;

б) его диагонали являются биссектрисами углов.

а) Дано: – параллелограмм, .

Доказать: – ромб.

Рассмотрим треугольник : в нем является одновременно и высотой (так как диагонали перпендикулярны), и медианой (так как диагонали в любом параллелограмме точкой пересечения делятся пополам). Значит, – равнобедренный. Из этого следует, что: . Если теперь воспользоваться тем, что в параллелограмме противоположные стороны равны, получаем, что: . То есть – ромб.

б) Дано: – параллелограмм, – биссектрисы углов параллелограмма.

Доказать: – ромб.

Рассмотрим треугольник : в нем является одновременно и биссектрисой (так как диагонали являются биссектрисами углов), и медианой (так как диагонали в любом параллелограмме точкой пересечения делятся пополам). Значит, – равнобедренный. Из этого следует, что: . Если теперь воспользоваться тем, что в параллелограмме противоположные стороны равны, получаем, что: . То есть, – ромб.

Задача 5.

Докажите, что ромб, у которого один из углов прямой, является квадратом.

Дано: – ромб,

Доказать: – квадрат.

Вспомним, что квадрат – это одновременно прямоугольник и ромб. Если говорить о сформулированном строгом определении, то квадрат – это прямоугольник, у которого все стороны равны. Равенство сторон следует из того, что данный четырёхугольник – ромб. Осталось доказать, что он является ещё и прямоугольником. По условию: (у любого параллелограмма противоположные углы равны). Кроме того, сумма соседних углов параллелограмма равна . Значит: . Отсюда мы получаем, что – прямоугольник, а значит, и квадрат.

На этом уроке мы изучили ромб и квадрат, а также рассмотрели их свойства и решили различные задачи, в которых встречаются ромб и квадрат.

Читайте также: